模块化多电平变流器开环环流抑制策略的渐进稳定性分析

赵 聪， 李耀华， 李子欣， 王 平， 楚遵方

(1.中国科学院电力电子与电气驱动重点实验室， 中国科学院电工研究所， 北京 100190；2. 中国科学院大学， 北京 100049)

模块化多电平变流器开环环流抑制策略的渐进稳定性分析

赵 聪1,2， 李耀华1， 李子欣1， 王 平1， 楚遵方1

(1.中国科学院电力电子与电气驱动重点实验室， 中国科学院电工研究所， 北京 100190；2. 中国科学院大学， 北京 100049)

模块化多电平变流器相间环流的存在使得桥臂电流产生畸变，一方面增加了变流器的损耗，另一方面对功率器件的安全工作范围也提出了更高的要求。本文从两个方面分析了开环环流抑制策略的渐进稳定性。首先证明了开环环流抑制策略的基本原理，并在此基础上提出开环环流抑制的一般原理，为模块化多电平变流器开环环流抑制的系统设计提供了理论依据。其次，相比实现起来更为简单的实际值调制环流抑制方法，本文的基于桥臂能量的开环环流抑制策略具有模块电容电压自平衡的特性，无需施加额外的控制；同时，从理论上证明了该开环环流抑制策略具备在不平衡条件下电容电压自平衡的特性，从而证明了该方法的渐近稳定性。最后，通过仿真验证了基于桥臂能量的开环环流抑制方法的稳定性和其模块电容电压自平衡特性的正确性。

模块化多电平变流器； 开环环流抑制； 渐进稳定

1 引言

相比传统的两电平或三电平拓扑的变流器，模块化多电平变流器(MMC)的拓扑结构具有明显的优势，主要表现在以下五个方面[1-4]：①变流器能够输出多电平，谐波特性好；②交流侧不再需要体积庞大、价格昂贵的滤波器装置；③模块化的设计使得电压和容量的提高变得相对容易；④分散的开关动作使得变流器的整体效率较高；⑤级联的模块对器件开关的一致性要求不高。因此MMC被认为最适合应用于高压大容量场合，尤其是基于电压源的高压直流输电领域(VSC-HVDC)[1-7]。在稳态运行的情况下，MMC的每相桥臂中除了含有直流电流和输出的基频交流电流外，还含有大量的偶次谐波环流，文献[8,9]对此进行了详尽的分析，其中以二次谐波为主。二次谐波环流的存在使得桥臂电流产生畸变，桥臂电流的有效值比直流与基波电流的叠加更大，对电力电子器件的安全工作范围提出了更高的要求，同时系统的通态损耗也会增大。所以在电力电子器件容量一定的情况下，通过施加控制抑制桥臂电流中的偶次谐波环流，能够在一定程度上提高变流器的容量，降低通态损耗。

关于MMC的环流抑制，国内外的很多文献分别提出了不同的方法[10-15]。文献[10]分别控制模块化多电平变流器上、下桥臂的能量之和和能量之差，利用电压补偿的方法，达到环流抑制的目的。文献[11]将三相二倍频环流进行了负序旋转坐标变换，利用电流闭环和PI调节器实现桥臂二倍频环流抑制，该方法只适用于三相系统，且不具备可扩展性。在文献[11]所提出方法的基础上，基于H∞理论，文献[12]设计了环流抑制的反馈参数，提高了系统的动态性能与鲁棒性。文献[13]利用桥臂环流都是偶次谐波的特点，基于PR调节器的选频特性，利用桥臂环流闭环和电压补偿的方法实现桥臂环流抑制。上述几种环流抑制方法虽然控制方法不同，但是它们都采用了闭环的控制策略。在实际系统中，闭环实现起来较为复杂，需要硬件电路间较为复杂的通信，同时闭环的方法存在着采样延时等可能对系统可靠性产生影响等缺点。

文献[14]提出了一种开环的环流抑制方法，但是并没有给出该方法实现环流抑制的原理。本文首先从理论上证明了文献[14]所述的开环环流抑制方法的原理，又比较了基于桥臂能量的环流抑制方法与文献[15]提出的实际值调制环流抑制方法的模块电容电压自平衡性。分析表明实际值调制方法不具备模块电容电压渐进稳定性，需额外施加较为复杂的控制；而本文所述的基于桥臂能量的开环环流抑制方法具备开环条件下模块电压的渐进稳定性。并且证明了初始时刻模块电容电压不相等的情况下，即使不施加额外的控制，模块电容电压还是会自动收敛到其平均值。最后，通过仿真验证了本文理论推导的正确性。

2 MMC的拓扑结构及其数学模型

2.1 MMC的拓扑结构

MMC的拓扑结构如图1所示。变流器由三相六个桥臂组成，每个桥臂由若干级联的功率模块与一个电感串联组成。每个功率模块的结构相同，都由两只带反并联二极管的开关器件串联再和一个直流电容并联构成。控制每个功率模块上、下开关的导通与关断，功率模块的输出电压就能在0与电容电压之间切换。通过协调控制MMC所有开关器件的导通与关断，变流器即可正确地输出三相电压。

图1 模块化多电平变流器的拓扑结构 Fig.1 Topology of MMC

2.2 MMC开环环流抑制方法

图2为模块化多电平变流器的单相等效电路。上桥臂与下桥臂级联模块可以等效为受控电压源。假设MMC的直流电压为Udc，直流电流为Idc。交流侧输出电压、电流的峰值为Uo和Io，功率因数角为φ，调制比为m。每个桥臂的模块数为N，桥臂电感和模块电容分别为L和C，功率模块电容电压的平均值为UC，桥臂等效电阻为R。在进行以下推导之前，首先对系统做出如下假设：

(1)系统对称运行，三相对称，每一相的上、下桥臂对称。

(2)三相的所有模块都相同，电压在所有模块中均匀分布。

(3)忽略桥臂中等效电阻对系统产生的影响。

图2 模块化多电平变流器单相等效电路Fig.2 Single phase equivalent circuit of MMC

文献[13]已经对开环的环流抑制方法做了详细介绍，这里不再赘述。本文在文献[13]的基础上没有考虑桥臂电阻对桥臂能量的影响。原因主要有以下两方面：①桥臂电阻很小，忽略其影响对桥臂能量的计算影响不大，而且能够简化桥臂能量的计算公式，在实际系统中能够减轻硬件负担；②在实际系统中，桥臂电阻是一个等效的概念，且影响桥臂电阻的因素很多，难以准确估算。因此基于这样的考虑得到MMC上、下桥臂总能量的瞬时值为：

式中，W0为桥臂能量的参考值；Wup和Wlow分别为只考虑相间环流为直流时上、下桥臂能量的瞬时值。

根据式(1)和式(2)计算得到上、下桥臂能量的瞬时值，然后计算与之对应的上、下桥臂模块电容电压分别如式(3)和式(4)所示。利用计算得到的电容电压代替上、下桥臂模块电容电压的给定值分别对上、下桥臂进行调制，进而生成各个模块的开关脉冲，就能够抑制桥臂环流中的偶次谐波分量。其控制框图如图3所示。

(3)

(4)

图3 MMC开环环流抑制框图 Fig.3 Block diagram of open loop circulating current suppression of MMC

3 环流抑制策略的渐进稳定性分析

本部分从理论上证明第2节中所述的基于桥臂能量的开环环流抑制策略的渐进稳定性。MMC在稳态运行时，桥臂环流中含有偶次谐波分量，文献[8,9]对MMC桥臂环流中的偶次谐波分量做了详尽的分析。因此，假设桥臂环流中含有所有偶次谐波分量，则MMC上、下桥臂的电流分别为：

式中，I2nf为相间环流中所有偶次谐波分量的幅值；φ2nf为其相位。

根据式(5)和式(6)计算得到上、下桥臂模块的瞬时功率为：

式中，Pup_n和Plow_n分别为考虑相间环流存在所有偶次谐波分量的上、下桥臂能量的瞬时值。对式(7)和式(8)积分，再加上桥臂能量的参考值，得到考虑所有次谐波环流的上、下桥臂能量的瞬时值：

Wup_n=W0+ΔWup+ΔWup_n

(9)

Wlow_n=W0+ΔWlow+ΔWlow_n

(10)

式中

(14)

(15)

MMC稳态运行时，根据基尔霍夫电压定律可知：

Udc=uup+ulow+2UL

(16)

式中，uup和ulow分别为上、下桥臂电压；UL为电感电压。因为桥臂模块电容电压的波动很小，因此忽略电容电压波动分量的无穷小项，可以认为桥臂能量的波动正比于桥臂模块电容电压的波动。因此，式(16)中uup、ulow和UL可以分别表示成如下形式：

(17)

(18)

(19)

式中，UC+ΔWup/(NCUC)和UC+ΔWlow/(NCUC)两项分别表示仅考虑相间环流为直流时的模块电容电压，即为桥臂的调制电压。而括号中的项是考虑相间环流存在所有偶次谐波分量的模块电容电压。将式(17)～式(19)代入式(16)化简得到：

(20)

式中

(21)

(22)

(23)

式(20)中等号左边为各个频率交流分量的和，等号右边为直流分量。因为桥臂电感的存在使得桥臂电流连续，即所有的I2nf不能突变，所以在这样的情况下，要使得交流量与直流量在每一时刻都相等，只能满足：

I2nf=0

(24)

式中，n为正整数。

综上，在桥臂环流中含有所有次谐波分量的情况下，采用基于桥臂能量的开环环流抑制方法能够抑制桥臂电流中除了直流分量和基频分量外的所有偶次谐波分量。即在假设相间环流只有直流分量的情况下，计算桥臂能量并由此计算得到模块电容电压，利用该电压作为模块电容电压的参考值调制MMC的上、下桥臂就能够实现开环的环流抑制。即使相间环流存在交流的偶次谐波分量，最终也能够收敛到其平均值。因此基于桥臂能量的开环环流抑制算法具备渐进稳定性。

4 模块电容电压渐进稳定性分析

文献[15]介绍了一种实际值调制方法，该方法的基本原理是利用实际测得的电容电压代替电容电压的给定值分别对MMC的上、下桥臂进行调制。如果测得的电容电压足够精确，那么此方法能够达到非常良好的环流抑制效果，且实现起来非常简单。但是，实际值调制方法存在电容电压不能自平衡的特点，需要施加额外的控制，且控制方法较复杂。文献[15]已经有详细的阐述，这里不再赘述。

本文所述的基于桥臂能量的开环环流抑制方法相比实际值调制算法，虽然实现起来相对复杂一些，但是该方法的模块电容电压是渐进稳定的，即使在上、下桥臂模块电容电压的初始值不相同的情况下，该方法也能够在不施加额外控制的条件下使模块电容电压收敛到其平均值。下面从理论上证明其模块电容电压的渐进稳定性。

因为MMC直流侧是一个电压源，假设初始状态上桥臂所有模块的电容电压是UC+Δu，下桥臂所有模块的电容电压是UC-Δu。以上桥臂为例，记

u0=UC+Δu

(25)

MMC开始工作时，采用式(3)和式(4)计算得到的电压作为上、下桥臂的模块电容电压分别调制两桥臂。根据基尔霍夫电压定律，施加在桥臂等效电阻上的电压近似为：

(26)

认为UCu≈UC，式(26)可以变成如下的形式：

(27)

式(27)由两部分组成，分别是交流分量和直流分量。同样地，定义其直流部分为有功分量，交流部分为无功分量。如果要使模块电容电压收敛，则必然是式(27)中的有功分量使模块电容电压的平均值变化，而式(27)中的无功分量只会使电容电压产生波动。所以在考虑模块电容电压的收敛问题时，只考虑其有功部分即可。有功部分在桥臂中产生的直流电流为：

(28)

i1会使得上桥臂模块电容放电，因此有：

(29)

式中，Δu1为有功部分在时间T内使得电容电压产生的变化量。将式(28)代入式(29)并积分得到：

(30)

记

(31)

可以得到经过时间T后，上桥臂模块的电容电压变为：

u1=UC+(1-α)Δu

(32)

利用计算得到的u1作为电容电压的初始值，按照式(26)～式(30)计算加在桥臂等效电阻上面的电压和电流，得到电容电压的变化量为：

Δu2=-αΔu(1-αΔu)

(33)

因此上桥臂模块在经过时间2T后的电容电压为：

u2=UC+(1-α)2Δu

(34)

以此类推，可以计算经过了足够长的时间，上桥臂模块电容电压的值为：

un=UC+(1-α)nΔu

(35)

式中

(36)

因为α是一个较小的量，因此经过了足够长的时间，un必然会收敛到UC，即

(37)

采用同样的分析方法和计算方法，还能够得到在上述假设条件下下桥臂模块的电容电压，如式(38)所示。经过了足够长的时间，下桥臂模块电容电压仍然能够收敛到UC。由此，证明了基于桥臂能量的开环环流抑制方法能够在不施加额外控制的情况下模块电容电压是渐进稳定的，即模块电容电压最终会收敛到平均值。由式(35)和式(38)可知，即使出现上、下桥臂不对称的情况，如上、下桥臂等效电阻不相等或模块电容值有差异等，只会影响α的值，进而影响模块电容电压的收敛速度，而不会影响最终的收敛结果。所以基于桥臂能量的开环环流抑制策略的模块电容电压是渐进稳定的。

(38)

5 仿真验证

为了验证基于桥臂能量的开环环流抑制算法的桥臂环流的收敛性以及其模块电容电压的自平衡特性，采用PSIM搭建了MMC的仿真模型，其仿真参数如表1所示。

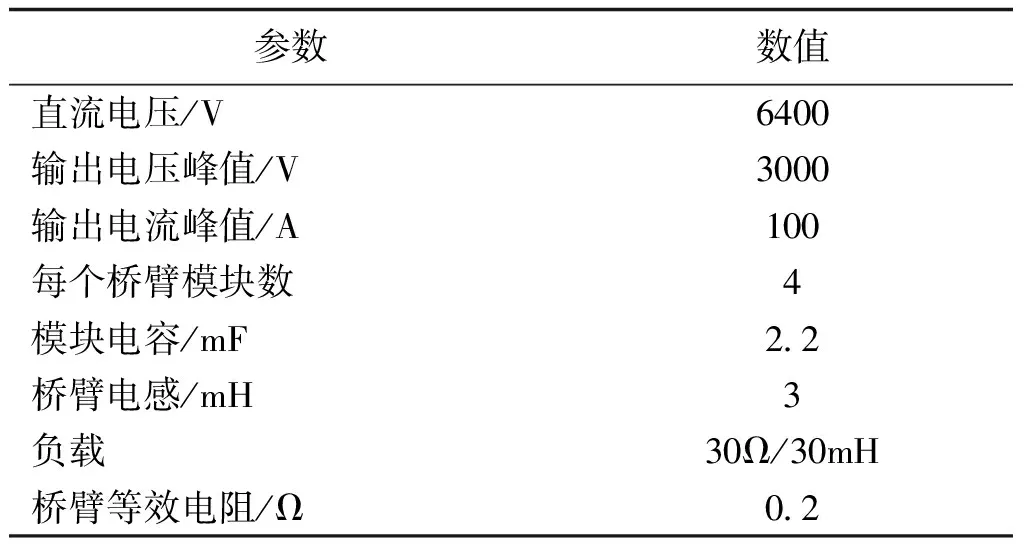
表1 单相MMC仿真参数Tab.1 Simulation parameters of one phase of MMC

由表1可知，每个模块的电容电压的平均值为1600V，系统初始时刻，采用电容电压给定值的调制方法，在0.2s时采用式(3)和式(4)计算得到的模块电容电压作为上、下桥臂电容电压的给定值分别对上、下桥臂进行调制，得到的相间环流波形如图4所示。可以看出，在不施加环流抑制算法的情况下，MMC的上、下桥臂间存在明显的环流，以二倍频波动为主，环流的峰值接近75A。在0.2s后，施加开环的环流抑制算法，相间环流逐渐减小，在经过约5个基波周期后，环流的交流分量逐渐收敛，MMC上、下桥臂间的环流几乎只有直流分量部分。验证了本文对环流渐进稳定性分析的正确性。

图5(a)和图5(b)分别为不施加环流抑制算法和施加基于能量的开环环流抑制算法得到的上、下桥臂电流波形。图5(a)的桥臂电流峰值接近80A，由于二倍频环流的存在使得桥臂电流发生畸变。图5(b)由于施加了环流抑制算法，桥臂电流的峰值接近70A，相比图5(a)降低了10A，因此环流抑制能够降低桥臂电流的峰值，降低换流器的通态损耗。此外，由于施加了环流抑制算法，MMC上、下桥臂间的偶次谐波环流得到了有效的抑制，因此，图5(b)中的桥臂电流几乎只包含直流分量和基波分量。

图4 环流抑制算法加入前后的环流波形Fig.4 Waveforms of circulating current before and after suppression algorithm implemented

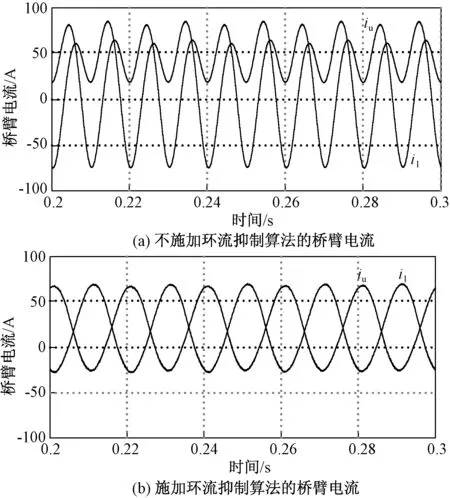
图5 环流抑制算法投入前后的桥臂电流波形Fig.5 Current waveforms of upper and lower arm before and after suppression algorithm implemented

采用电容电压给定值调制得到的模块电压和模块电压给定值的波形如图6(a)所示。因为模块的实际电压和给定值不相等，按照给定值计算得到的已开通模块的电压和与直流侧的电压不相等，这部分不平衡电压加在桥臂电感上产生桥臂间的环流的交流部分。采用式(3)计算得到的模块电容电压和上桥臂第一个模块的电压波形如图6 (b)所示。由图6 (b)可知，计算得到的模块电容电压与模块的实际电压几乎完全相同，因此，根据式(3)得到的模块电容电压作为电容电压的给定值计算得到的已开通模块的电压和与直流侧的电压相等，不会引起直流侧与MMC一相的不平衡，也就不会产生桥臂间的环流交流部分，即桥臂间的环流的交流部分会得到有效的抑制。上述分析验证了本文的开环环流抑制的一般原理的有效性，只要能够确定桥臂模块电容电压的瞬时值，用该电压值调制MMC的上、下桥臂就能够实现开环的环流抑制。此外，不加入环流抑制算法，由图6 (a)可知，模块电容电压的波动约为±50V，环流抑制算法投入后，模块电容电压的波动不超过±30V，因此环流抑制能够降低模块电容电压的波动。

图6 环流抑制算法投入前后的模块电压波形Fig.6 Module voltage waveforms before and after suppression algorithm implemented.

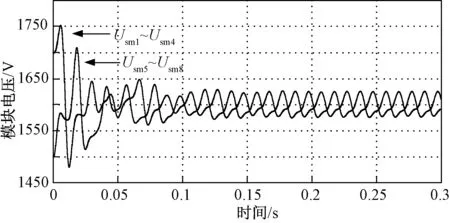
图7 模块电容电压自平衡性Fig.7 Module capacitor voltage self-balancing

采用基于桥臂能量的开环环流抑制算法，上桥臂所有模块的电容电压的初始值设为1700V，下桥臂所有模块的电容电压的初始值设为1500V，得到的仿真波形如图7所示。从图7可以看出，虽然初始阶段上、下桥臂模块电容电压不相等，但是经过了一段时间后，上、下桥臂模块电容电压都收敛到1600V左右，验证了关于基于桥臂能量的开环环流抑制算法模块电容电压渐进稳定性分析的正确性。

6 结论

本文详细分析了基于桥臂能量的开环环流抑制算法，在考虑桥臂所有次谐波环流的情况下对其环流抑制的基本原理进行了数学证明。理论分析表明，该方法能够使环流的交流部分逐渐收敛到零。一般地，只要能够实时确定桥臂模块电容电压的瞬时值，利用该模块电容电压调制MMC的上、下桥臂就能够在开环的情况下实现环流抑制。本文为MMC的开环环流抑制设计提供了理论依据。

本文分析了实现起来较为简单的实际值调制算法，虽然满足环流抑制的基本原理，但是其模块电容电压不具备自平衡性，需要施加额外控制，使系统设计变得复杂。而基于桥臂能量的开环环流抑制算法的模块电容电压是渐进稳定的。理论分析表明，即使出现上、下桥臂模块电容电压不相等的情况，本文所述的开环环流抑制算法也会使上、下桥臂模块电压收敛到其平均值。由此，证明了该环流抑制算法的全局渐进稳定性。

[1] A Lesnicar, R Marquardt. An innovative modular multilevel converter topology suitable for a wide power range[A]. 2003 IEEE Bologna Power Tech Conference Proceedings [C]. Bologna, Italy, 2003.3:1-6.

[2] A Nami, J Liang, F Dijkhuizen, et al. Modular multilevel converters for HVDC applications: Review on converter cells and functionalities [J]. IEEE Transactions on Power Electronics, 2015, 30 (1): 18-36.

[3] 罗永捷，李耀华，李子欣，等(Luo Yongjie, Li Yaohua, Li zixin, et al.). 多端柔性直流输电系统直流故障保护策略(DC short-circuit fault protection strategy of multiterminal-HVDC systems) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34 (12):1-6.

[4] M A Perez, J Rodriguez, E J Fuentes, et al. Predictive control of AC-AC modular multilevel converters [J]. IEEE Transactions on Industry Electronics, 2012, 59 (7): 2832-2839.

[5] S Allebord, R Hamerski, R Marquardt. New transformerless scalable modular multilevel converters for HVDC-transmission [A]. 2008 IEEE Power Electronics Specialists Conference [C]. 2008. 174-179.

[6] D Peftitsis, G Tolstoy, A Antonopoulos, et al. High-power modular multi-level converters with SiC JFETs [J]. IEEE Transactions on Power Electronics, 2012, 27 (1): 28-36.

[7] 汤广福，罗湘，魏晓光(Tang Guangfu, Luo Xiang, Wei Xiaoguang). 多端直流输电与直流电网技术(Multi-terminal HVDC and DC-grid Technology) [J]. 中国电机工程学报(Proceedings of the CSEE)，2013，33(10):8-17.

[8] Kalle Ilves, Antonios Antonopoulos, Staffan Norrga, et al. Steady-state analysis of interaction between harmonic components of arm and line qantities of modular multilevel converter [J]. IEEE Transactions on Power Electronics, 2012, 27 (1): 57-68.

[9] 周月宾，江道灼，郭捷，等(Zhou Yuebin, Jiang Daozhuo, Guo Jie, et al.). 模块化多电平换流器子模块电容电压波动与内部环流分析(Analysis of sub-module capacitor voltage ripples and circulating currents in modular multilevel converters) [J]. 中国电机工程学报(Proceedings of the CSEE)，2012, 32(24):8-14.

[10] A Antonopoulos, Lngquist, H-P Nee. On dynamics and voltage control of the modular multilevel converter[A]. 13th European Conference on Power Electronics and Applications (EPE) [C]. Barcelona, Spain, 2009. 1-10.

[11] Q Tu, Z Xu, L Xu. Reduced switching-frequency modulation and circulating current suppression for modular multilevel converter [J]. IEEE Transactions on Power Delivery, 2011, 26 (3): 2009-2017.

[12] B Bahrani，S Debnath，M Saeedifard. Circulating current suppression of the modular multilevel converter in a double-frequency rotating reference frame [J]. IEEE Transactions on Power Electronics, 2016, 31 (1):783-792.

[13] Z Li, P Wang, Z Chu, et al. An inner current suppressing method for modular multilevel converter [J]. IEEE Transactions on Power Electronics, 2013, 28 (11): 4873-4879.

[15] Zunfang Chu, Yaohua Li, Ping Wang, et al. A novel circulating current suppressing method of modular multilevel converter[A]. Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), IEEE Conference and Expo [C]. Beijing, China, 2014. 1-5.

Asymptotic stability analysis of open-loop circulating current suppression of modular multilevel converter

ZHAO Cong1,2, LI Yao-hua1, LI Zi-xin1, WANG Ping1, CHU Zun-fang1

(1. Key Laboratory of Power Electronics and Electrical Drive, Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)

The circulating current of modular multilevel converter (MMC) makes arm current distorted. It increases converter losses and also threatens safe operating of power devices. This paper analyzes the open-loop circulating current suppression method based on arm energy from two aspects. Firstly, the fundamental of the open-loop circulating current suppression algorithm is proved. This paper also proposes general principle of open-loop circulating current suppression which provides theoretical basis for system design of MMC. Secondly, compared with the actual value modulation algorithm which is easier to implement, the method based on arm energy in this paper has module capacitor voltage self-balancing features without additional control. This paper also proves that the open-loop circulating current suppression based on arm energy has module voltage self-balancing features theoretically. Hence, the global asymptotic stability of the open-loop circulating current suppression is proved. Finally, the method and its module capacitor voltage self-balancing are verified by simulation.

modular multilevel converter； open loop circulating current suppression； asymptotic stability

2016-03-30

国家高技术研发发展计划(863计划)项目(2013BAG19B00-04-01)

赵 聪(1988-)， 男， 满族， 辽宁籍， 博士研究生， 研究方向为模块化多电平换流器与柔性直流输电技术等； 李耀华(1966-)， 男， 河南籍， 研究员， 博士生导师， 研究方向为电力电子变流技术、 电机分析与控制技术等。

TM72

A

1003-3076(2016)10-0001-08