基于粒子群与极限学习机的电能质量信号特征选择与识别

黄南天， 卢国波， 王玉强， 赵振峰， 李 旭， 张卫辉

(1. 东北电力大学电气工程学院， 吉林省 吉林市 132012； 2. 国网冀北电力有限公司检修分公司， 北京 102488； 3. 甘肃电力公司武威供电公司， 甘肃 武威 733000)

基于粒子群与极限学习机的电能质量信号特征选择与识别

黄南天1， 卢国波1， 王玉强2， 赵振峰2， 李 旭3， 张卫辉1

(1. 东北电力大学电气工程学院， 吉林省 吉林市 132012； 2. 国网冀北电力有限公司检修分公司， 北京 102488； 3. 甘肃电力公司武威供电公司， 甘肃 武威 733000)

高效准确地分类电能质量扰动信号是处理电能质量问题的关键。为降低特征计算量，提高分类器分类效率，本文提出一种基于粒子群与极限学习机的电能质量特征选择与识别方法。首先，通过S变换对电能质量扰动信号进行重构与变换，并在此基础上提取特征；然后，以极限学习机的分类精度和选择特征个数作为适应度函数，通过粒子群算法在高维特征空间中寻优，剔除不相关和冗余的特征，保留对扰动识别有效果的特征，由此，确定最优分类子集；最后，使用最优特征子集构成极限学习机的输入向量，训练分类器，并采用优化后的分类器分类电能质量信号。仿真实验表明，新方法能够将维度为25的原始特征集合缩减到8维，且在不同噪声环境下保持综合分类准确率为99.33%。

电能质量； S变换； 粒子群算法； 极限学习机； 特征选择

1 引言

随着分布式可再生能源、非线性负荷与电力电子设备的大量接入，电能质量(Power Quality，PQ)问题日益受到电力工作人员的重视[1]。PQ问题多表现为电压质量问题，包括电压暂升、电压暂降、电压中断、电压闪变、暂态振荡和谐波等。而在实际系统中，还经常发生含有多种扰动的复合扰动。

准确分类PQ信号是治理PQ问题的前提和基础。分类时，需先对原始扰动信号进行变换与处理，提取出表征扰动信号特点的分类特征。常用的方法有S变换(S-Transform，ST)[2]、小波变换(Wavelet Transform，WT)[3]和短时傅里叶变换(Short Time Fourier Transform，STFT)[4]等。ST分析中采用的高斯窗口的高度和宽度是动态变化的，其具有良好的时-频特性与抗噪能力，可以提取丰富的时-频特征用于分类PQ信号[5,6]。但是过多的特征也会造成分类器维度过高、分类效率与准确率下降的缺陷。因此，需要对原始特征集合进行特征选择，以降低特征集合维度与分类器复杂度，提高分类效率。

PQ信号分类方法主要包括支持向量机[2]、BP神经网络[7]和概率神经网络[8]等。这些方法具有良好的鲁棒性，但是参数设置复杂，时间或空间复杂度较高，实现困难。极限学习机(Extreme Learning Machine，ELM)需要优化的参数少，实现起来简单、迅速，能够满足PQ信号分类问题的要求。

为简化PQ信号分类器结构，提高分类效率与准确率，本文提出一种基于粒子群优化算法(Particle Swarm Optimization，PSO)与ELM的PQ信号特征选择与分类方法。首先利用S变换对原始扰动信号进行时-频分析，并根据变换结果提取原始扰动特征；其次，将PSO和ELM相结合，以ELM分类精度和选择特征个数构建适应度函数，并以适应度函数值最大为准则，在特征空间中进行寻优，以降低特征维数；然后，使用最优特征子集构成ELM的输入向量，训练ELM；最后，采用该模型识别包含2种复合扰动在内的8类PQ信号，并通过仿真实验验证新方法的有效性。

2 S变换与特征提取

2.1 S变换原理

ST是在连续快速傅里叶变换(Successive Fast Fourier Transform, SFFT)和WT的基础上发展而来，相较其他方法具有更好的抗噪能力和特征表现能力，因而广泛地应用于PQ扰动信号识别。

设输入信号为h(t)，其连续ST为：

(1)

式中

(2)

表1 电能质量扰动信号仿真模型

式中，w(τ-t,f)为高斯窗口；t为时间；τ是一个参数，控制高斯窗口在时间轴上位置；f为频率。ST的逆变换为：

(3)

由式(1)和(2)可得到离散ST，表达形式如下：

(4)

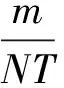
2.2 扰动信号的S变换

[2]构建电压暂降(C1)、电压暂升(C2)、电压中断(C3)、电压闪变(C4)、暂态振荡(C5)、谐波畸变(C6)、谐波含电压暂降(C7)和谐波含电压暂升(C8)八类PQ信号模型，通过MATLAB仿真生成PQ信号，信号采样率3.2kHz，基频50Hz。扰动信号模型见表1。

2.3 特征提取

从经过ST处理的仿真信号中提取25种特征用于构建原始特征集合。所有特征的具体描述如下。

特征1(F1)：STMM各列最大幅值中的最大值。

特征2(F2)：STMM各列最大幅值中的最小值。

特征3(F3)：STMM各列最大幅值的均值(Mean)。

特征4(F4)：STMM各列最大幅值的标准差(STD)。

特征5(F5)：STMM各列最大幅值的归一化幅值因数(Af)。

特征6(F6)：100Hz以上各频率对应最大幅值曲线的标准差。

特征7(F7)：100Hz以上各频率对应最大幅值曲线的最大差。

特征8(F8)：100Hz以上各频率对应最大幅值曲线的最小差。

特征9(F9)：100Hz以上各频率对应最大幅值曲线的最大值与最小值的差。

特征10(F10)：高频部分曲线偏度(Skewness)。

特征11(F11)：高频部分曲线峭度(Kurtosis)。

特征12(F12)：各个频率对应最大幅值曲线的标准差。

特征13(F13)：各个频率对应最大幅值曲线的均值。

特征14(F14)：各个频率对应幅值标准差曲线的均值。

特征15(F15)：各个频率对应幅值标准差曲线的标准差。

特征16(F16)：低频部分对应幅值标准差曲线的标准差。

特征17(F17)：高频部分对应幅值标准差曲线的标准差。

特征18(F18)：谐波总含量(THD)。

特征19(F19)：原始信号1/4周期能量跌落幅度。

特征20(F20)：原始信号1/4周期能量上升幅度。

特征21(F21)：基频幅值的标准差。

特征22(F22)：中频部分最大值。

特征23(F23)：700～1000Hz高频段能量。

特征24(F24)：形态学去噪后高频频段能量。

特征25(F25)：FFT功率谱中频段80～470Hz能量。

设xi为扰动样本向量X中某一个采样点的电压幅值，1≤i≤N，N为扰动样本所包含的采样点数。特征相关计算公式如下：

在计算能量相关的特征时，设xij为矩阵中第i行第j列的元素，N1≤i≤N2，M1≤j≤M2，N1、N2、M1和M2分别为计算相关能量特征时所需子矩阵的起始行、终止行、起始列和终止列。相关能量特征计算公式如下：

3 极限学习机

极限学习机是一种单隐含层前馈神经网络(Single-hidden Layer Feedforward Neural Network，SLFN)。与传统神经网络训练算法不同，ELM输入层与隐含层的连接权重以及隐含层各神经元节点的偏置是随机产生的，训练过程中无需调整改变。ELM需要调整的参数少，分类效率、准确率高，适用于PQ信号分类。典型的单隐含层前馈神经网络的结构如图1所示。

图1 典型的单隐含层前馈神经网络结构Fig.1 Typical structure of single hidden layer feedforward neural network

给定一组数据：S={(x1,y1),…,(xp,yp)}，其中xi∈Rn为训练样本输入，yi∈Rm为训练样本值，i=1,2,…,p，则包含有l个隐含层神经元，且激活函数为g(x)的ELM数学模型为：

(5)

式中，αi为输入节点与第i个隐含层节点的连接权值向量；βi为第i个隐含层节点与输出节点的连接权值向量；bi为第i个隐含层节点的偏置。

式(5)可以化简为：

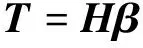
(6)

式中，T=[t1,t2,…,tp]T；H为隐含层输出矩阵：

(7)

Huang等人[9]证明，若隐含层神经元个数l等于训练集样本数，则对于任意的α和b，SLFN将以零误差逼近训练样本，即：

(8)

当样本数p过大时，为了降低计算复杂度，隐含层神经元个数l取值一般小于样本数p，此时SLFN的训练误差将小于任意ε>0，即：

(9)

隐含层与输出层的连接权值β的求解如下：

(10)

其最小二乘解为：

(11)

式中，H†为H的Moore-Penrose广义逆。

4 基于PSO的ELM特征选择

4.1 PSO算法原理

PSO首先在解空间中初始化一群粒子，每个粒子代表一个潜在的最优解，且由位置、速度和适应度值三个参数表征。粒子通过跟踪个体极值Pbest和群体极值Gbest来更新上述三个参数，并根据新粒子的适应度值更新Pbest和Gbest。

假设搜索空间为D维，粒子群共含有N个粒子，其中第i个粒子表示为Xi=(xi1,xi2,…,xiD)，即粒子i在搜索空间中的位置；Vi=(vi1,vi2,…,viD)表示粒子i的速度；记Pi=(Pi1,Pi2,…,PiD)为粒子i的个体极值；群体极值则记为Pg=(Pg1,Pg2,…,PgD)。迭代过程中，通过式(12)和式(13)更新粒子的速度和位置：

(12)

(13)

式中，w为惯性权重；d=1,2,…,D；i=1,2,…,N；k为当前迭代次数；c1、c2称为加速度因子，是非负的常数；r1、r2为随机数，取值范围为[0，1]。每个粒子的位置和速度都被限制在一定的范围内，超过该范围则取其边界值，避免粒子的盲目搜索。

4.2 PSO-ELM特征选择

将PSO与ELM相结合，进行PQ信号特征选择。由于特征选择可以简化为一个“0-1”组合优化问题，所以在初始化粒子时，将每一维特征对应的粒子位置随机初始化为“0”或者“1”，“0”表示该维特征被淘汰，“1”则表示特征被选中。粒子每次更新位置后，按如下规则调整位置向量中元素：

(14)

因为特征选择的目标是在选择尽可能少的特征的条件下，获得尽可能高的分类准确率，因此PSO适应度函数应同时考虑选择特征的个数和分类精度，且更加侧重分类精度。新方法适应度函数设计如下：

fitness_function=0.7×rate×100-0.3×n

(15)

式中，rate为分类准确率；n为特征子集维度。

采用新方法特征选择过程如下：

(1)初始化粒子；

(2)根据适应度函数计算每一个粒子的适应度值，确定个体极值Pbest和群体极值Gbest；

(3)根据Pbest和Gbest更新粒子位置与速度，将每一个粒子所表示的特征子集作为ELM的输入向量，并检验该ELM在测试集上的分类精度；

(4)重复步骤(2)和步骤(3)，直至达到最大迭代次数。

整个特征选择过程中，以采用不同特征组合后，分类具有随机噪声与随机参数值的样本集的整体准确率为特征分类效果评判标准，而不必考虑具体特征对特定类型扰动的分类效果，这样降低了特征选择方法的复杂度。算法流程如图2所示。

5 实验仿真

实验所用数据均由MATLAB7.10产生。为获得能够满足不同噪声环境分类需要的最优特征子集，分别仿真生成含30～50dB随机噪声的训练样本，每种扰动信号500组，用于特征选择；选用信噪比分别为50dB、40dB和30dB的测试集，每类各100组，验证特征选择结果的分类效果。为提高方法的鲁棒性，全部实验过程中，训练集与测试集中样本参数均采用覆盖相关参数范围的随机值，以验证方法在不同参数条件下的有效性。

实验中，PSO最大迭代次数为300次，粒子速度更新公式中c1=c2=1.49445，速度边界值分别为vmax=0.5、vmin=-0.5。

由于PSO算法中粒子规模会对适应度值有所影响，因此，分别分析不同规模下PSO算法的适应度值，如图3所示。由图3可知，适应度值最高点出现在粒子规模为4的时候，此时选择出的特征子集为FS1={F2，F5，F6，F9，F17，F19，F20，F21}，含8个特征；具有次优适应度值的粒子规模为11，特征子集为FS2={F2，F5，F7，F13，F14，F17，F18，F19，F21，F22，F23}，含11个特征。上述2个特征子集在不同信噪比下的分类精度如表2所示。由表2可知，FS1的分类准确率优于FS2，且特征数更少。可见，具有最优适应度值的选择结果最适于PQ信号分类，而冗余特征的加入不仅会增加分类器时间和空间复杂度，还会影响分类器分类准确率。

图3 粒子群规模对适应度值的影响Fig.3 Influence of particle swarm size on fitness values

特征子集特征个数分类准确度(%)50dB40dB30dB综合准确率(%)FS18995993899139933FS21199389888949742

此外， ELM的激活函数选为Sigmoid时，新方法根据分类准确率，确定隐含层神经元个数l。不同噪声环境下，l对分类精度的影响如图4所示。由图4可见，当l为75时，分类准确率达到最高，且趋于稳定。而训练的时间代价则随着l的增加而不断提升，因此，新方法取l=75。

图4 隐含层神经元个数对分类精度的影响Fig.4 Effects of number of hidden layer neurons on classification accuracy

为进一步验证新方法的有效性，采用与表2所用相同试验样本，与其他三种方法[10-12]进行对比，结果如表3所示，其中，MFST为多分辨率快速S变换，DT为决策树，RVM为相关向量机，PNN为概率神经网络。由表3可知，新方法在处理特定信噪比下实验样本时，准确率高于文献[10]与文献[11]方法，略低于文献[12]方法。

表3 特征选择效果比较

为客观分析新方法的扰动识别效果，将三类对比方法的识别的扰动种类均设为本文使用的八类。

考虑到实际分类环境下信号信噪比无法预知，因此，具有随机噪声水平的信号更能够验证方法的实际应用效果。因此，对比试验中训练分类器时，采用具有30～50dB随机噪声的训练样本，每类各500组；测试时，使用具有随机噪声信噪比为30～50dB的测试信号，每类各300组，验证各种方法的分类精度。在随机噪声环境下，四种方法的扰动识别效果如表4所示。

表4 相同条件下扰动识别效果对比

由表4可见，随机噪声环境下，新方法具有最好的扰动识别效果，相较于采用决策树分类的文献[12]方法，具有更好的泛化能力，且新方法更加适合噪声水平未知的实际PQ扰动信号分类需求。

6 结论

本文提出一种基于PSO与ELM的新型PQ信号特征选择和识别方法。新方法将特征维度由25维缩减到8维，极大降低了训练分类器所耗费的时-空代价，相较现有方法，新方法在分类具有随机噪声的测试集时，具有最高的分类准确率，更适合实际环境工作需要。

参考文献 (References)：

[1] 白鸿斌，王瑞红，王真，等(Bai Hongbin, Wang Ruihong, Wang Zhen, et al.). 风电场接入电网的电能质量分析方法研究及案例分析 (Analysis method of power quality with the integration of wind power and case study) [J]. 东北电力大学学报(自然科学版) (Journal of Northeast Dianli University Natural Science Edition)，2008，28(6)：33-37.

[2] 黄南天，徐殿国，刘晓胜 (Huang Nantian, Xu Dianguo, Liu Xiaosheng).基于S变换与SVM的电能质量复合扰动识别(Identification of power quality complex disturbances based on S-transform and SVM) [J].电工技术学报 (Transactions of China Electrotechnical Society)，2011，26(10)：23-30.

[3] 欧阳森，王建华，耿英三，等(Ouyang Sen, Wang Jianhua, Geng Yingsan, et al.).基于小波和神经网络的电能质量辨识方法 (Power quality classification based on wavelet transform and neural network) [J].电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2003，22(3)：32-36.

[4] 徐永海，赵燕 (Xu Yonghai, Zhao Yan).基于短时傅里叶变换的电能质量扰动识别与采用奇异值分解的扰动时间定位 (Identification of power quality disturbance based on short-term Fourier transform and disturbance time orientation by singular value decomposition) [J]. 电网技术 (Power System Technology)，2011，8(8)：174-180.

[5] 吕干云，冯华君，汪晓东，等 (Lv Ganyun, Feng Huajun, Wang Xiaodong, et al.).基于S变换和人工神经网络的电能质量扰动识别 (PQ disturbances identification based on S-transform and ANN) [J].仪器仪表学报(Chinese Journal of Scientific Instrument)，2006，27(S3)：2281-2283.

[6] Naik C A, Kundu P. Power quality disturbance classification employing S-transform and three-module artificial neural network [J]. International Transactions on Electrical Energy Systems, 2014, 24(9): 1301-1322.

[7] 欧阳森 (Ouyang Sen).改进遗传算法和神经网络在电能质量扰动识别中的应用 (Improved genetic algorithm and neural network’s application in the recognition of power quality disturbances) [J].电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2005，24(3)：13-17.

[8] Lee C Y, Shen Y X. Optimal feature selection for power-quality disturbances classification [J]. IEEE Transactions on Power Delivery, 2011, 26(4): 2342-2351.

[9] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: Theory and applications [J]. Neurocomputing, 2006, 70(1-3): 489-501.

[10] 赵立权，谢妮娜 (Zhao Liquan, Xie Nina).基于小波变换和改进的RVM的电能质量扰动分类 (Classification of power quality disturbances based on wavelet transform and improved RVM) [J].电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2013，32(4)：74-78.

[11] 唐求，王耀南，郭斯羽，等 (Tang Qiu, Wang Yaonan, Guo Siyu, et al.).基于S变换与PNN的电能质量多扰动检测 (Power quality disturbance detection based on S-transform and PNN) [J].仪器仪表学报(Chinese Journal of Scientific Instrument)，2009，30(8)：1668-1673.

[12] 黄南天，张卫辉，蔡国伟，等 (Huang Nantian, Zhang Weihui, Cai Guowei, et al.).采用改进多分辨率快速S变换的电能质量扰动识别(Power quality disturbances classification with improved multiresolution fast S-transform) [J].电网技术 (Power System Technology)，2015，39(5)：1412-1418.

Feature selection and identification of power quality signals based on particle swarm optimization and extreme learning machine

HUANG Nan-tian1, LU Guo-bo1, WANG Yu-qiang2, ZHAO Zhen-feng2, LI Xu3, ZHANG Wei-hui1

(1. College of Electrical Engineering, Northeast Dianli University, Jilin 132012, China; 2. Maintenance Branch, State Grid Jibei Electric Power Co. Ltd., Beijing 102488, China; 3. Wuwei Power Supply Company, Gansu Power Company, Wuwei 733000, China)

Efficient and accurate classification of power quality disturbance signal is the key to deal with power quality problems. In order to reduce the computation quantity and improve the efficiency of classification, a power quality feature selection and recognition method based on particle swarm optimization and extreme learning machine is proposed. Firstly, the power quality disturbance signal is reconstructed and transformed by S transform, and then the feature is extracted. Secondly, using particle swarm optimization to search for the optimal feature subset in high dimensional feature space based on the fitness function which uses the classification accuracy of extreme learning machine and the selected feature number. The optimal feature subset contains only these features which have effect on the classification. Finally, the optimal feature subset is used as extreme learning machine’s input to train the classifier. After that, the power quality signal is classified by the optimized classifier. Simulation experiments show that the new method can reduce the original feature set of 25 to 8 dimension, and maintain the overall classification accuracy in 99.33%.

power quality; S-transform; particle swarm optimization; extreme learning machine; feature selection

2015-08-24

国家自然科学基金(51307020)、 吉林省科技发展计划(20150520114JH)资助项目

卢国波(1992-)， 男， 江西籍， 硕士研究生， 研究方向为电能质量分析; 黄南天(1980-)， 男， 吉林籍， 副教授/硕导， 博士， 主要研究方向为电能质量分析、 新能源并网技术等。

TM741

A

1003-3076(2016)07-0055-07