“国粹”脸谱、“蛋圆”与中考压轴题

☉山东省枣庄市第十五中学　王介寅　李其明



“国粹”脸谱、“蛋圆”与中考压轴题

☉山东省枣庄市第十五中学王介寅李其明

中国，是拥有五千年历史的古国，它具有十分丰富的文化传承，其中京剧就是一门重要的艺术，常常受到外国友人的青睐.看到图1所示的京剧脸谱了吗？其实它们可以看成是一个半圆与抛物线的一部分组合成的封闭图形，我们称之为“蛋圆”（形状类似于鸡蛋）.

图1

2015年山东省威海市中考数学试题：我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”（形状类似于鸡蛋），如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线.如图2，点A、B、C、D分别是“蛋圆”与坐标轴的交点，AB为半圆的直径，点M为圆心，A点的坐标为（-2，0），B点的坐标为（4，0），D点的坐标为（0，-4）.

（1）你能求出经过点C的“蛋圆”切线的解析式吗？试试看.

（2）请你求出“蛋圆”抛物线部分的解析式，并写出自变量x的取值范围.

（3）你能求出经过点D的“蛋圆”切线的解析式吗？若能，请写出过程；若不能，请说明理由.

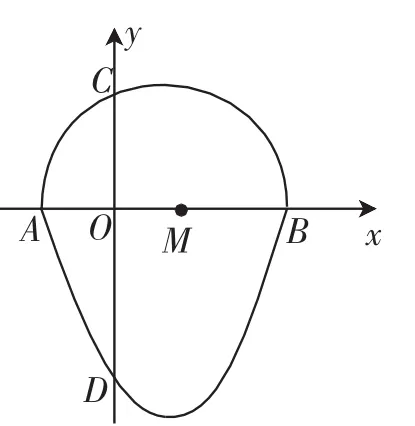
图2

一、考题解法探究

分析：（1）由点A、B的坐标，用交点式设出二次函数的解析式，把D的坐标代入即可.自变量的取值范围是点A、B之间的数.

（2）先设出切线与x轴交于点E.利用直角三角形相应的三角函数求得EM的长，进而求得点E的坐标，把C、E的坐标代入一次函数的解析式即可求得所求的解析式.

（3）设出所求函数的解析式，让它与二次函数组成方程组，消除y，让根的判别式为0，即可求得一次函数的比例系数k.

解：（1）如图3，设经过点C的“蛋圆”切线CE交x轴于点E，连接CM，则CM⊥CE.

由A点的坐标为（-2，0），B点的坐标为（4，0），AB为半圆的直径，点M为圆心，得M点的坐标为（1，0），则AO= 2，BO=4，OM=1.

因为CO⊥x轴，所以CO2=AO·OB，解得CO=2

由CM⊥CE，CO⊥x轴，得CO2=EO·OM，解得EO=8，则E点的坐标是（-8，0），则切线CE的解析式为y=x+

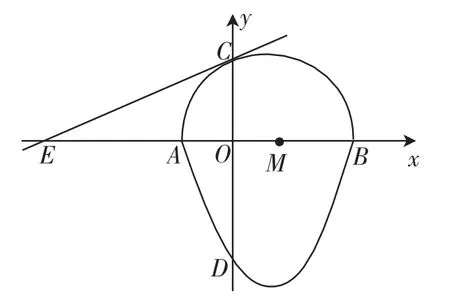
图3

（2）设抛物线的解析式为y=a（x+2）（x-4）（a≠0）.又点D（0，-4）在抛物线上，则a=x2-x-4，自变量的取值范围是：-2≤x≤4.

（3）设过点D（0，-4）的“蛋圆”切线的解析式为：y= kx-4（k≠0）.

点评：本题以半圆与抛物线合成的封闭图形“蛋圆”为背景，考查一次函数、二次函数有关性质，解题过程中涉及解一元一次方程、一元二次方程、方程组相关知识与技能，是一道综合性很强的试题.

二、考题的引申

引申1：其他条件不变，求被y轴截得的弦CD的长.

分析：连接AC、BC，由已知的A、B、C、D四点的坐标，进而求出AO、BO、DO的长，在直角三角形ACB中，利用射影定理可求出CO的长，进而可求出CD的长.

引申2：其他条件不变，已知点E是“蛋圆”上一点（不与点A、点B重合），点E关于x轴的对称点是F，若点F也在“蛋圆”上，求点E的坐标.

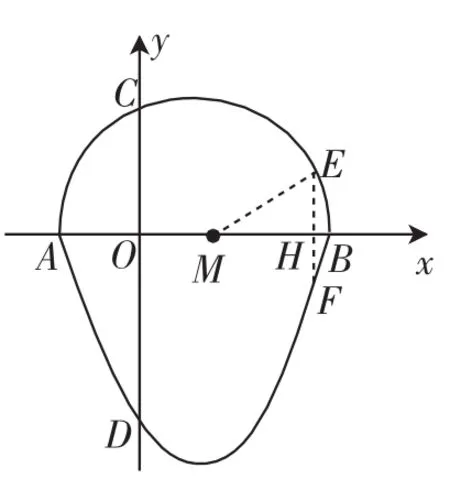
图4

分析：如图4，假设点E在x轴上方的“蛋圆”上，EF与x轴交于点H，连接EM.由HM2+EH2=EM2，点F在二次函数y=x2-x-4的图像上，可得方程组，再根据对称性求解.

引申3：其他条件不变，求“蛋圆”在第一象限的图像上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC的面积的最大值；若不存在，请说明理由.

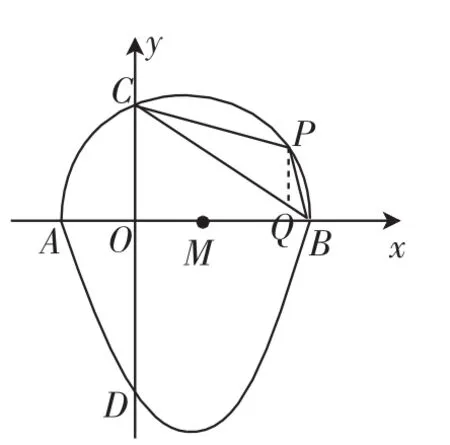
图5

分析：如图5，过点P作PQ∥y轴，交BC于Q，用待定系数法得到直线BC的解析式，再根据三角形的面积公式和配方法得到△PBC的面积的最大值.