让旋转开出“旋转之花”

王晶晶

摘 要：初中数学图形变换之一的旋转以其“变化莫测”成为学生学习的难点之一.作为一线数学教师。常常困惑于如何找到探究此类问题的一般解法，进而引导学生从旋转“变化”中理出一条“不变”的分析规律，成为学生的解题经验。

关键词：初中数学；旋转；例题

一、巧用“旋转”的性质求边

在《旋转》一章中，有这样一道大家熟知的例题：

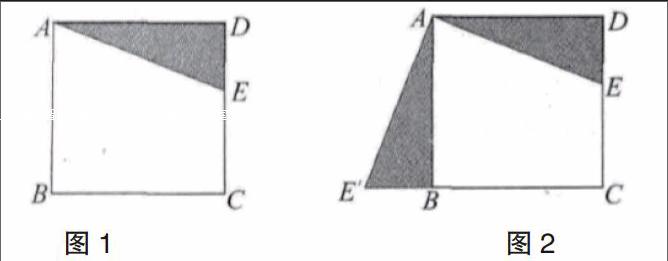
如图1，E上是正方形ABCD中CD边上任意一点，以点A为中心，△ADE顺时针旋转900，画出旋转后的图形。

关键是确定△ADE三个顶点的对应点，即它们旋转后的位置.显然，点A的对应点是它本身.由正方形的性质易知，旋转后点D与点B重合设点E的对应点为E，因旋转前后的图形全等，故∠ABE=∠ADE=900，BE=DE。如图2，在CB的延长线上取点E，使BE=DE，连接AE，则△ABE即为所求。

由于正方形具有一些特殊性质，所以对上述题目实施多角度、全方位的变式，成为各地中考试卷的重要“题眼”下面举例说明。

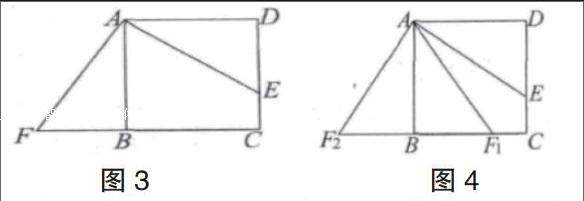
例1巳知正方形ABCD中，点E在边DC上，DE=2，EC=1，把线段AE绕点A旋转，使点E落在直线BC上的点F处，则F，C两点的距离为________.

解析：有的同学可能会作出如卡错误的解答：如图3，FC=FB+BC=5，賴法出现以偏概全的错误题中只说“直线BC：的点”，故需分两种情况讨论：如图4所示，当点F在线段BC上时，旋转得到F1点，则F1C=1；当点F在线段CB的延长线上时，旋转得到F2点，则F2B=DF=2，F2C=F2B+BC=5.综上可知，F，C两点的距离为1或5.

点评：本例考查学生对旋转概念的全面理解，在分情况讨论上设置了陷阱。

二、巧用“旋转”的性质求角

根据旋转的性质，我们知道对应点到旋转中心的距离相等，对应线段的长度相等，对应角的大小相等，旋转前后图形的大小和形状没有改变，在性质中“对应线段的长度相等，对应角的大小相等”，我们可以利用这个性质将要求的角转换成求旋转图形的对应角，然而图形在“旋转”运动中，往往会产生特殊的图形，我们再通过这些特殊的图形来求对应角，进而求未知角，这样问题就迎刃而解了。通过“旋转”运动，可以将毫无思路的问题明朗化，有助于他们找到准确的解题思路或方向，达到事半功倍的作用。我们一起来看这样的一个例子：

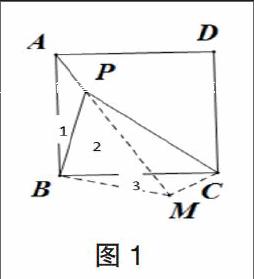
如图1，P为正方形ABCD内一点，且 PA=1，PB=2，PC=3. 求∠ APB 的度数。

分析：我们分析题目，发现题目所给的 条件是边长，而所要求的是角度，显然，只 有将这些边长组合成特殊三角形（直角三角 形或等腰三角形），通过特殊三角形的已知 角来求未知角。要想构造特殊三角形，我们 知道，通过“旋转”运动可以得到，从而化 未知角为已知角来解决问题。又因为所给的 图形是正方形，我们发现，正方形的边长是 相等的，旋转时有一条对应边正好与正方形 的另一边重合，形成了对应的图形△CMB， 从而可将求∠ APB 转化成求对应角∠ CMB。 且在“旋转”运动的过程中，构成了两个 特殊的三角形，即等腰直角△PBM、直角 △PMC，正好∠CMB由∠BMP和∠PMC组成， 把∠ BMP 和∠ PMC 放在△ PBM 和△ PMC 中看问题，我们的问题就可以巧妙的解决啦！ 具体解答过程如下：

解法一：因为四边形ABCD为正方形， 所以 BA=BC，将△ APB 绕点 B 顺时针方向旋 转 90°，则点 A 与点 C 重合，设点 P 落到的 位置为点M，得到△CMB，连接PM，由旋转可知：

△ APB ≌△ CMB.

∴∠ 3= ∠ 1，∠ CMB= ∠ APB. MC=PA=1，MB=PB=2.

∵四边形 ABCD 为正方形 .

∴∠ 1+ ∠ 2= ∠ ABC=90° .

∴∠ 3+ ∠ 2=90° .

即△ PMB 为等腰直角三角形 .

∴ PM=，PB=2 ， ∠ BMP=45° 又 在 △ PMC 中， PM2 + CM2 = 2 （2）2 +12=8+1=9， PC2 =32=9.

∴ PM2 + CM2 = PC2 ，

∴∠ PMC=90°.

∴∠ CMB= ∠ PMC+ ∠ BMP

=90°+45°=135°.

∴∠ APB=135°. 答：∠ APB 的度数是 135°。

解 法 二： 同 理， 如 图 2，

我 们 将 △PBC绕点B逆时针方向旋转90°，则 点C与点A重合，设点P落到的位置为点 M，得到△AMB，连接PM，由旋转可知： △BPC≌△BMA.此旋转方法也可以解决同 样的问题。

“旋转”的性质在几何证明中不仅仅只 有这些，它在其他方面也有比较广泛的运用， 本文只是结合教学过程中出现的一些问题， 总结了一下自己的经验与心得体会，目的更 多的是提醒自己今后在教学中，不要仅仅把 目光放在如何应付眼前的考试，只是教会学 生如何画图是不够的，还应该启发学生们如 何运用“旋转”运动的知识来巧解几何问题， 熟练掌握图形运动的性质和特点，发散学生 的思维，提高他们思考问题的能力，培养他 们对数学的兴趣，为今后的学习做准备。