高中学生在导数就用中的几个误区



高中学生在导数就用中的几个误区

◇山东刘明运

导数作为研究函数的有力工具,在处理曲线的切线、函数的单调性、极值、最值等方面起着举足轻重的作用．但是在导数的应用过程中由于对导数知识掌握不全面、不深刻,学生容易陷入如下不易察觉的误区．

1过一条曲线上的任意一点,必能做出切线

那么在每一点处连续的函数是否有切线呢?也不一定,例如f(x)=|x|+1，在x=0处没有切线．

2函数在某点不可导,该点不存在切线

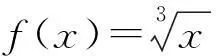
3如果曲线存在切线,切线只有1条

求在曲线上已知点的切线,那就只有1条．因为如果函数在该点处可导,可知在曲线上的切点是确定的,斜率也是唯一的．如果是过曲线上或曲线外的某点的切线,求出来的切线就可能不止1条了．例如:求过曲线y=x3-2x上的点(1,-1)的切线方程.所求切线方程为x-y-2=0或5x+4y-1=0.可以发现直线5x+4y-1=0并不以(1,-1)为切点,实际上是经过了点(1,-1)且以(-1/2,7/8)为切点的直线.这说明过曲线上一点的切线,该点未必是切点,切线未必只有1条．

4某区间上递增,则f′(x)≥0恒成立

其实, 当a=3时,g′(x)=1/4-1/x2在x=2时无意义,所以a=3不符合,正确答案应为(3,+∞)．那么可导的函数在某区间M上单调递增(减),则f′(x)≥0(f′(x)≤0)还是f′(x)>0(f′(x)<0)恒成立呢?这就要从函数单调性的充要条件说起:

1) 对于可导函数y=f(x),如果方程f′(x)=0在某个区间上至多有有限个孤立解,那么在这个区间上,f(x)为增函数的充要条件是f′(x)≥0;f(x)为减函数的充要条件是f′(x)≤0．

2) 连续函数y=f(x)在闭区间[a,b]与开区间(a,b)上具有相同的单调性．

5导数为0的点一定是极值点

要解决这个问题,首先看下面的概念:函数的导数为0的点称为函数的驻点(驻点也称为稳定点)极大点和极小点统称为极值点．可导函数f(x)的极值点必然在函数f(x)的稳定点的集合之中,反之,不成立,即稳定点不一定是极值点．

错解导函数f′(x)=3x2+2ax+b,因为函数f(x)在x=1处有极值10,可得

上述解题忽略了一个细节,解题过程中只用到f′(1)=0和f(1)=10,这能说明它是极值点吗?当a=-3、b=3时,f′(x)=3x2-6x+3=3(x-1)2≥0,函数f(x)在R上是增函数,显然x=1不是函数f(x)的极值点;验证当a=4、b=-11时,x=1是函数的极值点．故a+b=-7．

综上,导数以其工具性决定了应用的广泛性,把导数作为工具研究曲线的切线、函数的单调性与极值,简洁、高效且具有操作性．但我们要掌握好导数这个工具,在应用时要多思考、多研究,全面深刻的使用它,以防止出现“意外”．

(作者单位：山东省济南市历城第一中学)