利用空间向量证明“平行”与“垂直”



利用空间向量证明“平行”与“垂直”

■左婷

用向量法解决立体几何问题，是空间向量的一个具体应用，体现了向量的工具性，这种方法可把复杂的推理证明转化为空间向量的运算，降低了空间想象演绎推理的难度，体现了由“形”转“数”的转化思想。本文就利用空间向量证明“平行”与“垂直”这一视角进行例析。

一、利用空间向量证明平行问题

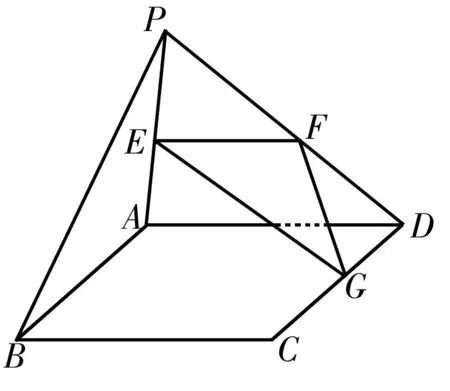
图1

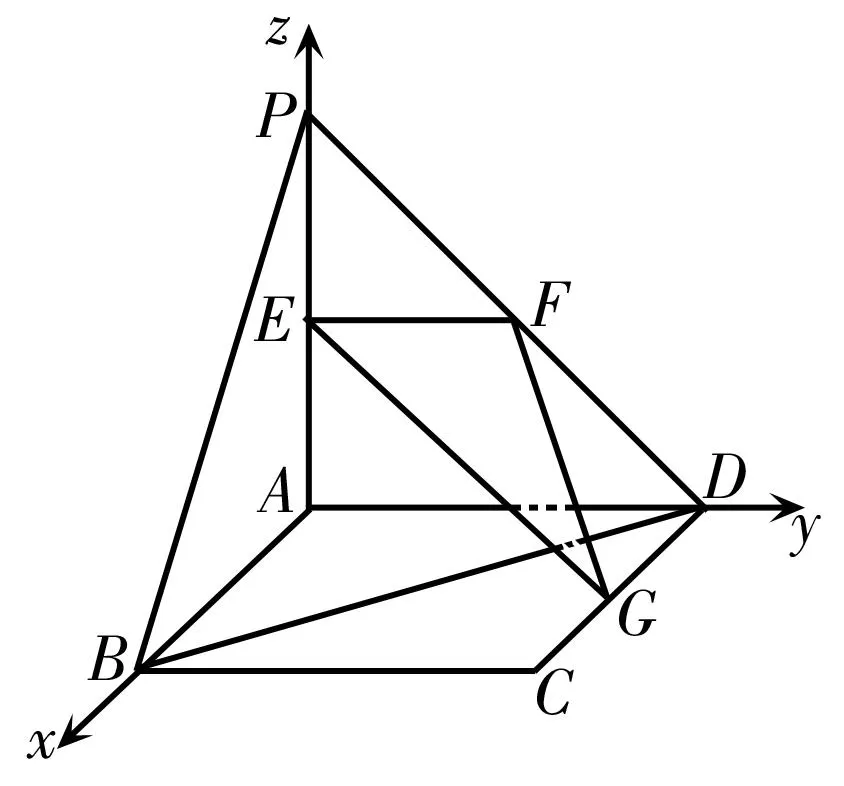
图2

例1如图1所示，平面PAD⊥平面ABCD，ABCD为正方形，△PAD是直角三角形，且PA=AD=2，E、F、G分别是线段PA、PD、CD的中点。求证：PB∥平面EFG。

证明:因为平面PAD⊥平面ABCD，且ABCD为正方形，所以AB，AP，AD两两垂直。以A为坐标原点，建立如图2所示的空间直角坐标系A-xyz，则A(0，0，0)，B(2，0，0)，C(2，2，0)，D(0，2，0)，P(0，0，2)，E(0，0，1)，F(0，1，1)，G(1，2，0)。

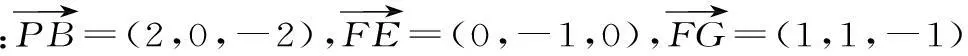
规律方法:(1)恰当建立坐标系，准确表示各点与相关向量的坐标，是运用向量法证明平行和垂直的关键。

(2)证明直线与平面平行，只需证明直线的方向向量与平面的法向量的数量积为零，或证直线的方向向量与平面内的不共线的两个向量共面，或证直线的方向向量与平面内某直线的方向向量平行，然后说明直线在平面外即可。这样就把几何的证明问题转化为向量运算。

二、利用空间向量证明垂直问题

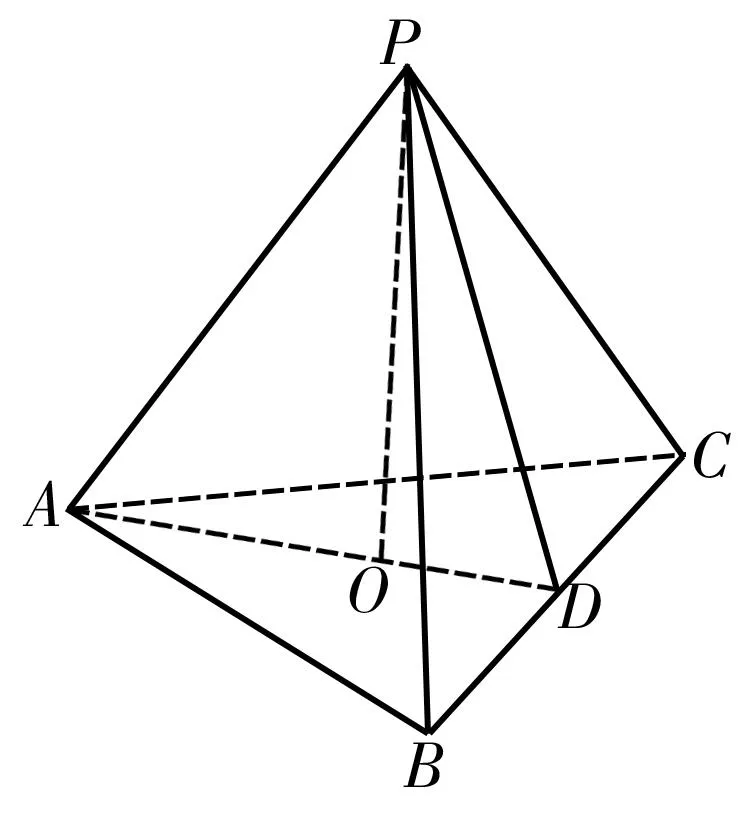
图3

例2如图3，在三棱锥P-ABC中，AB=AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上。已知BC=8，PO=4，AO=3，OD=2。

(1)证明：AP⊥BC；

(2)若M是线段AP上一点，且AM=3。试证明：平面AMC⊥平面BMC。

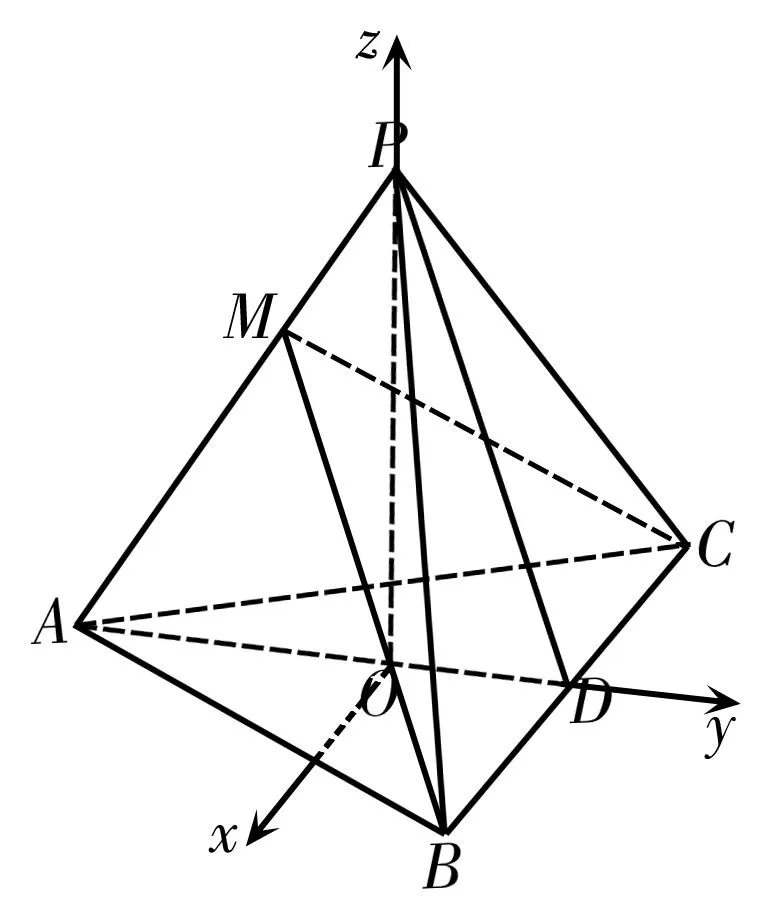
图4

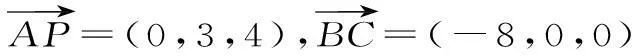
规律方法:(1)利用已知的线面垂直关系构建空间直角坐标系，准确写出相关点的坐标，从而将几何证明转化为向量运算。其中灵活建系是解题的关键。

(2)其一，证明线线垂直，只需要证明两条直线的方向向量垂直。其二，证明线面垂直，只需证明直线的方向向量与平面内不共线的两个向量垂直即可，当然也可证直线的方向向量与平面法向量平行。其三，证明面面垂直：①证明两平面的法向量互相垂直；②利用面面垂直的判定定理，只要能证明一个平面内的一条直线的方向向量为另一个平面的法向量即可。

作者单位：江苏省高邮市第一中学