双星图的Ramsey数的上界

余　培， 李雨生

(同济大学 数学系，上海 200092)



双星图的Ramsey数的上界

余培， 李雨生

(同济大学 数学系，上海 200092)

摘要：对给定的两个图G和H, Ramsey数R(G,H)是最小的正整数N，使得对完全图KN的边任意红/蓝着色，则或者存在红色子图G，或者存在蓝色子图H.双星B(m,n)为直径是3,有两个中心顶点, 其顶点度分别为m+1和n+1的树.得到，当n>m时,R(B(m,n))<2n+m+2；当n=m或n=m+1时, R(B(m,n))=2m+n+2.

关键词：Ramsey 数; 树; 双星

1引言

本文中研究的图均为简单图.对给定的两个图G和H,Ramsey数R(G,H)是最小的正整数N,使得对完全图KN任意的红/蓝 边着色,则或者存在红色子图G,或者存在蓝色子图H.当G=H时，简记R(G,G)=R(G).

Ramsey数是组合数学中公认的难题.以Tn表示具有n个顶点的树.作为最简单的图类,其Ramsey数R(Tn)格外引人关注.两种经典的树图,星K1,n-1和路Pn的Ramsey数已知如下,分别见文献[1-2]和文献[3].

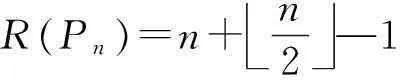
R(Pn)=n+n2—1

引理2设n为大于1的正整数,则.

Erdös和Faudree等[4]得到R(Tn)的最优下界4n/3-1，对于上界有一个经典的猜想.

猜想1设n是大于1的正整数.是否任何树Tn都满足R(Tn)≤R(K1,n-1).

这个猜想没有获得任何证实,但可以看到R(Pn)是满足猜想1的.本文研究一类特殊的树: 双星图B(m,n).它是直径为3,有两个中心顶点,其顶点度分别为m+1和n+1的树.直观地讲，就是用一条边连接两个星K1，m和K1，n的中心点.如没有特殊说明，文中假设n≥m.对于B(m,n),文中求出了它的Ramsey上界,同时得到它也满足猜想1.

如果用k种颜色对图G的顶点进行着色,使得两个相邻的顶点有不同的颜色则称图G是可k真着色的.将真着色中的最小k称为图G的色数,记为x(G).用s(G)表示对G进行x(G)点着色时,相同颜色顶点类所含顶点数的最小值.Burr[5]得到Ramsey数的一般下界.

引理3若图G和H满足,G连通且G的顶点数大于等于s(H), 则:

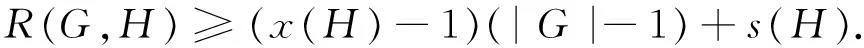
对B(m,n)而言,x(B(m,n))=2,s(B(m,n))=m+1, 故可得到推论1的结果.

推论1当正整数n≥m时,R(B(m,n))≥2m+n+2.

在有关双星B(m,n)的Ramsey数的研究中, Guo和Volkman[6]得到R(B(1,n))的值.最近Bahlas和Spencer[7]得到下面的结果：①当m=2,n≥3时，R(B(2,n))≤2n+3.②当m≥3,m+2≤n≤2m-1时，R(B(m,n))≤2n+m+1.③当m≥3,n∈{m,m+1} 时，R(B(m,n))≤2m+n+1.

本文扩充了①～③的结果,同时指出文献[7]中得到的③中的结果是有问题的，这里修正为定理1并给出相应的证明.

定理1当n=m或n=m+1时,R(B(m,n)) =2m+n+2.

定理2当n≥m时，R(B(m,n))≤2n+m+1.

2证明

给定图G, 用|G|表示图G的顶点个数,N(v)和d(v)分别表示顶点v的邻域和度数. 给图G的边红/蓝着色时,记Nr(v)={u∈G| {u,v}是红边}是v的红邻域，dr(v)=|Nr(v)|为其红色度.类似地定义蓝邻域Nb(v)和蓝色度db(v).

在证明定理1之前,先引入引理4并给出相应的证明.

引理4已知正整数m,n,N满足n≥m, 2m+n+2≤N≤2m+2n+1.给完全图KN的边任意红/蓝着色,若不含单色B(m,n),则对KN中任意点v, 均有:

证明若存在顶点v满足dr(v)≥m+n+1, 则对Nr(v)中任意点u,均有dr(u)≤m,否则存在红色B(m,n).由于dr(u)+db(u)=N-1,故db(u)≥N-1-m≥m+n+1. 类似的分析可知,对Nb(u)中任意w均有db(w)≤m,dr(w)≥m+n+1.若Nr(v)和Nb(u)的交集非空，取x为其中一点，则dr(x)≤m且dr(x)≥m+n+1，矛盾.若Nr(v)和Nb(u)的交集为空，则：N≥|Nr(v)|+|Nb(u)|+1≥2(m+n+1)+1，矛盾.故对任意点v均有dr(v)≤m+n,类似地db(v)≤m+n.此时若KN中存在一点v满足dr(v)=m+n，则db(v)=N-1-(m+n)≥m+1. 对Nr(v)中任意点w,由于db(w)≤m+n，故dr(w)≥N-1-(m+n)≥m+1.若w与Nb(v) 之间存在红边，则存在w,v为中心点的红色B(m,n),矛盾.故Nr(v)与Nb(v)之间全是蓝边，此时{v∪Nr(v)}与Nb(v)之间包含蓝色完全二部图Km+n+1,m+1, 从而有蓝色B(m,n),矛盾.故对KN中任意点v,均有dr(v)≤m+n-1，类似的,db(v)≤m+n-1.

由dr(v)+db(v)=N-1可知N-m-n≤dr(v),db(v)≤m+n-1,证毕.

定理1的证明当n=m或n=m+1时,由推论1可知，R(B(m,n))≥2m+n+2. 下面只需证：R(B(m,n))≤2m+n+2.

记N=2m+n+2,给完全图KN的边任意红/蓝着色，记R和B为所得到的红色子图和蓝色子图.假设不含单色B(m,n),由引理4知，对KN中任意点v,均满足dr(v),db(v) 落在区间[m+2,m+n-1]内,其中m+2≥n+1.不妨设dr(v)=m+n-a，db(v)=m+1+a,其中1≤a≤n-2.考虑Nr(v)与Nb(v)之间边的连接情况.Nr(v)中的任意点w到Nb(v)中至多有a条红边，否则将会存在一个以w,v为中心点的红色B(m,n)；类似地Nb(v)中任意点w到Nr(v)中至多有n-a-1条蓝边，否则将存在一个以v,w为中心的蓝色B(m,n).因此Nr(v)与Nb(v)之间最多有a(m+n-a)+(n-a-1)(m+1+a)条边，但经验算：

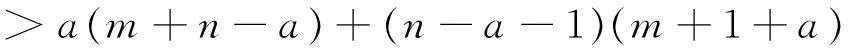
这产生矛盾.故原假设不成立，从而存在单色B(m,n).证毕.

定理2的证明记N=2n+m+1, 给完全图KN的边任意红/蓝着色，记R和B为所得到的红色子图和蓝色子图.

情形1m+1≤n≤2m-1时,用类似于定理1的证明或直接引用文献[7]中的结果，可知此时定理成立.

情形2n≥2m时，对m进行归纳证明.当m=1时，N=2n+2.对KN中任意点v,由于dr(v)+db(v)=N-1=2n+1,故可设dr(v)≥n+1.在Nr(v)在中选取集合A满足|A|=n+1，设C=V(KN)(v∪A) 则 |C|=n.若A中存在一点u与C中点连红边，则存在红色B(1,n),定理成立.否则，A和C可形成蓝色完全二部图Kn+1,n,故存在蓝色B(1,n).因此当m=1时，定理成立.

假设当m≤k-1时，定理成立.

当m=k时, 假设不含单色B(k,n)，由引理4知，对KN中任意点v，均有dr(v),db(v)落在区间[n+1,k+n-1]内.由归纳假设知，R(B(k-1,n))<2n+k+1=N.由Ramsey数的定义可知,存在一个单色B(k-1,n),不妨假设为红色.设该B(k-1,n)

的中心点为u,v且dr(u)=k,dr(v)=n+1.记A=Nr(v){u},C=V(KN)V(B(k-1,n)),则|A|=|C|=n.由于不存在红色B(k,n),故u到C之间全是蓝边.因db(u)≥n+1>|C|，故u到A之间中存在蓝边.选取A中点w使得{u,w}是蓝边.考虑集合{Aw}与C之间边的连接情况.由于不存在单色B(k,n),故{Aw}中的任意点x到C中至多有k-1条红边, 否则将存在以x,v为中心点的红色B(k,n)；类似的,C中任意点y到{Aw}中至多有k-1条蓝边,否则集合{y,Nb(y)∩(Aw)}与集合{u,w,Cy}可形成以y,u为中心点的蓝色B(k,n).故{Aw}与C之间最多有(k-1)(n-1)+(k-1)n条边.但当n≥2k时

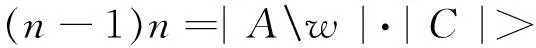
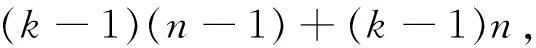
矛盾.故原假设不成立，从而存在单色B(k,n).

综上所述，该定理成立.证毕.

注应用定理1于B(1,1)=P4可得R(B(1,1))=5, 该结果与由引理2得到的R(P4)=5一致.注意到定理1中的限制n=m或n=m+1是必要的.实际上,因为K1,n+1是B(m,n)的子图,所以有R(B(m,n))≥R(K1,n+1)≥2n+1. 因此该定理中的等式不可能对(相对于m)很大的n成立.

参考文献:

[1]Burr S, Roberts J. On the Ramsey numbers for stars [J]. Utilitas Mathematica, 1973, 4: 217.

[2]Chvátal V, Harary F. Generalized Ramsey theory for graphs II, small diagonal numbers [J]. Proceeding of the American Mathematical Society, 1972, 32: 389.

[3]Gerencser L, Gyárfas A. On Ramsey-type problems[J]. Annals of the University of Bucharest. Mathematical Series, 1967, 10: 167.

[4]Erdös P, Faudree R, Rousseau C,etal. Ramsey number for Brooms [J]. Congressus Numerantiu., 1982, 35: 283.

[5]Burr S. Ramsey numbers involving graphs with long suspended paths [J]. Journal of the London Mathematical Society, 1981, 24: 405.

[6]Guo Y, Volkmann L. Tree-Ramsey numbers[J]. The Australasian Journal of Combinatorics, 1995, 11: 169.

[7]Bahls P, Spencer T. On the ramsey numbers of trees with small diameter [J]. Graphs and Combinatorics, 2013, 29: 39.

An Upper Bound for the Ramsey Numbers of Bistars

YU Pei, LI Yusheng

(Department of mathematics, Tongji University, Shanghai 200092, China)

Abstract：For two given graphs G and H, Ramsey number R(G,H) is the smallest integer N such that any red/blue edge-coloring of KN contains a red copy of G or a blue copy of H. Let a bistar B(m,n) be a tree of diameter three with two central vertices of degree m+1 and n+1, respectively. It is shown that R(B(m,n))<2n+m+2 for n>m; and R(B(m,n))=2m+n+2 for n=m or n=m+1.

Key words：Ramsey number; tree; bistar

文献标志码：A

中图分类号：O157.5

收稿日期：2015-04-24

第一作者： 余培(1993—), 男, 博士生, 主要研究方向为组合数学与图论.E-mail: yupeizjy@163.com