“南水”双屈服面模型的两点修正

王庭博， 陈生水， 傅中志

(1. 同济大学，土木工程学院， 上海 200092; 2. 南京水利科学研究院， 岩土工程研究所， 南京 210029；

3. 水利部土石坝破坏机理与防控技术重点实验室， 南京 210024)



“南水”双屈服面模型的两点修正

王庭博1,2， 陈生水2,3， 傅中志2,3

(1. 同济大学，土木工程学院， 上海 200092; 2. 南京水利科学研究院， 岩土工程研究所， 南京 210029；

3. 水利部土石坝破坏机理与防控技术重点实验室， 南京 210024)

摘要：基于堆石料大型三轴试验数据，分析研究了其切线模量和切线体积比与应力状态的关系，建立了切线模量和体积比与应力比之间的函数关系式，并将其引入“南水“双屈服面弹塑性模型中.运用修正模型对不同应力路径下堆石料的大型三轴压缩试验结果进行了模拟，结果表明，修正模型在未增加参数的情况下较好克服了原模型在描述堆石料应力-应变关系，特别是剪胀(缩)特性方面的不足，可更好地模拟堆石料的强度和变形特性.

关键词：双屈服面； 弹塑性模型； 切线模量； 切线体积比； 堆石料

堆石料具有压实性能好、透水性强、填筑密度大、抗剪强度高、沉陷变形小、承载力高等工程特性，在高土石坝建设中得到了广泛应用[1].早在20世纪70年代，Duncan等[2]就在试验基础上提出了著名的双曲线模型，描述堆石料的应力-应变关系，并因其参数确定简单在土石坝应力-变形有限元计算中得到广泛运用.但Duncan模型本质是非线性弹性模型，对堆石料体变的模拟通过泊松比与应力状态的关系实现，故很难合理反映堆石料显著的剪胀(缩)特性.此外，Duncan模型运用于实际工程时通常会高估大坝沉降.为克服上述问题，沈珠江以Duncan模型为基础，采用抛物线描述堆石料的体变曲线，并引入两个屈服面分别反映剪胀和剪缩特性，建立了“南水” 双屈服面弹塑性本构模型[3].由于“南水”模型参数同样只需常规三轴压缩试验确定，且预测的大坝位移与实测资料更为吻合，故在国内高土石坝工程中得到普遍运用和广泛认可.然而，抛物线型体变曲线会明显高估堆石料的峰后体胀，特别是在描述较为松散的堆石料或高围压下堆石料三轴压缩试验时差异明显.此外，模型中破坏比参数的运用使试样始终处于硬化状态，很难正确模拟堆石料的破坏过程.

张丙印等[4]提出了堆石体的修正Rowe剪胀方程，并将其用于描述堆石料体变特性，使用常规和复杂应力路径的三轴试验成果对修正后的模型进行了验证，结果显示其较好克服了采用抛物线型体变曲线模拟的缺陷.米占宽等[5]提出了考虑颗粒破碎的剪胀方程，对南水模型中切线体积比μt进行了修正，提出了考虑颗粒破碎的粗颗粒料本构模型，通过与三轴试验成果的对比分析表明了其所提模型可较好地反映体变特性，但修正后比原模型增加了3个参数.

本文基于堆石料大型三轴试验数据，建立了切线模量Et和切线体积比μt分别与应力比η的关系，将峰值应力比Mf和临胀应力比Mc两个控制应力峰值和体变特性的特征应力比引入“南水”双屈服面弹塑性本构模型，结果表明，修正模型在未增加参数的情况下较好克服了原模型在描述堆石料应力-应变关系，特别是剪胀(缩)特性方面的不足，可更好地模拟堆石料的强度和变形特性.

1“南水”双屈服面模型

1.1Et和μt的表达式

“南水”双屈服面模型沿用了Duncan-Chang模型切线模量Et表达式，即

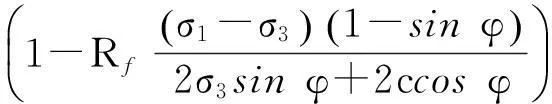
(1)

式中:(σ1-σ3)为轴向偏应力；K为量纲一的初始弹性模量系数；n为初始弹性模量随围压变化的幂次；pa为标准大气压，pa=101 kPa；Rf为破坏比，c和φ分别为材料的粘聚力和内摩擦角，对于堆石料c=0，内摩擦角由式(2)计算：

(2)

式中：φ0是围压σ3为大气压力pa时的峰值摩擦角；Δφ是围压σ3增加一个数量级时峰值摩擦角降低的角度.卸荷一再加荷条件下切线模量由式(3)计算：

(3)

式中：Kur为量纲一的卸载回弹模量系数；n为量纲一幂次.而体积应变与轴向应变(εv-ε1)的关系曲线则假定为抛物线[6]，如图1所示，其方程为

(4)

式中:εvd为最大体缩应变；εd为与最大体缩应变所对

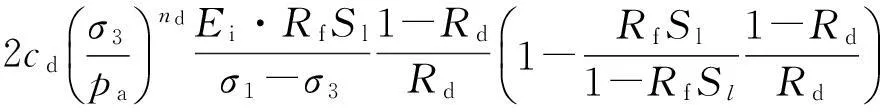
(5)

式中:Ei是初始弹性模量;Sl是应力水平，cd，nd，Rd为3个试验参数，分别代表σ3=1个大气压时的最大体应变，体应变随σ3变化的幂次和最大体应变发生时的应力比，由式(6)—(7)决定：

(6)

(7)

“南水”双屈服面模型共涉及9个计算参数，分别为c、φ、Rf、K、Kur、n、cd、nd、Rd，均可由三轴固结排水剪切试验得出.

图1　三轴试验曲线的拟合

1.2“南水”双屈服面模型模拟结果

采用“南水”双屈服面模型对某高土石坝堆石料三轴试验结果进行模拟.“南水”双屈服面模型参数见表1.试验数据和模拟结果见图2.其中，散点为试验结果，曲线为模拟结果.从图2a轴向应力应变关系曲线中可以看出，尽管堆石料峰值摩擦角是根据试验资料直接整理得出的，但式(1)并未合理反映出堆石料的破坏特点，主要原因是式(1)中破坏比参数(Rf<1)的运用，使材料在应力水平达到1时切线模量仍然始终为正，无法模拟应力不变条件下，应变无限增长的破坏特点；“南水”双屈服面模型的另一个不足之处是，无论在低围压还是高围压状态下，均高估了堆石料的剪胀，如图2b所示，显然，抛物线型体变曲线不能很好模拟堆石料的剪胀(缩)规律.

表1　三轴试验模型计算参数

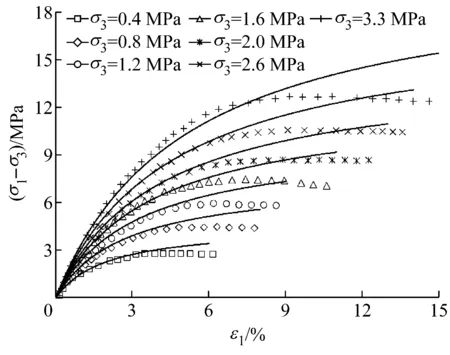
a (σ1-σ3)-ε1拟合曲线

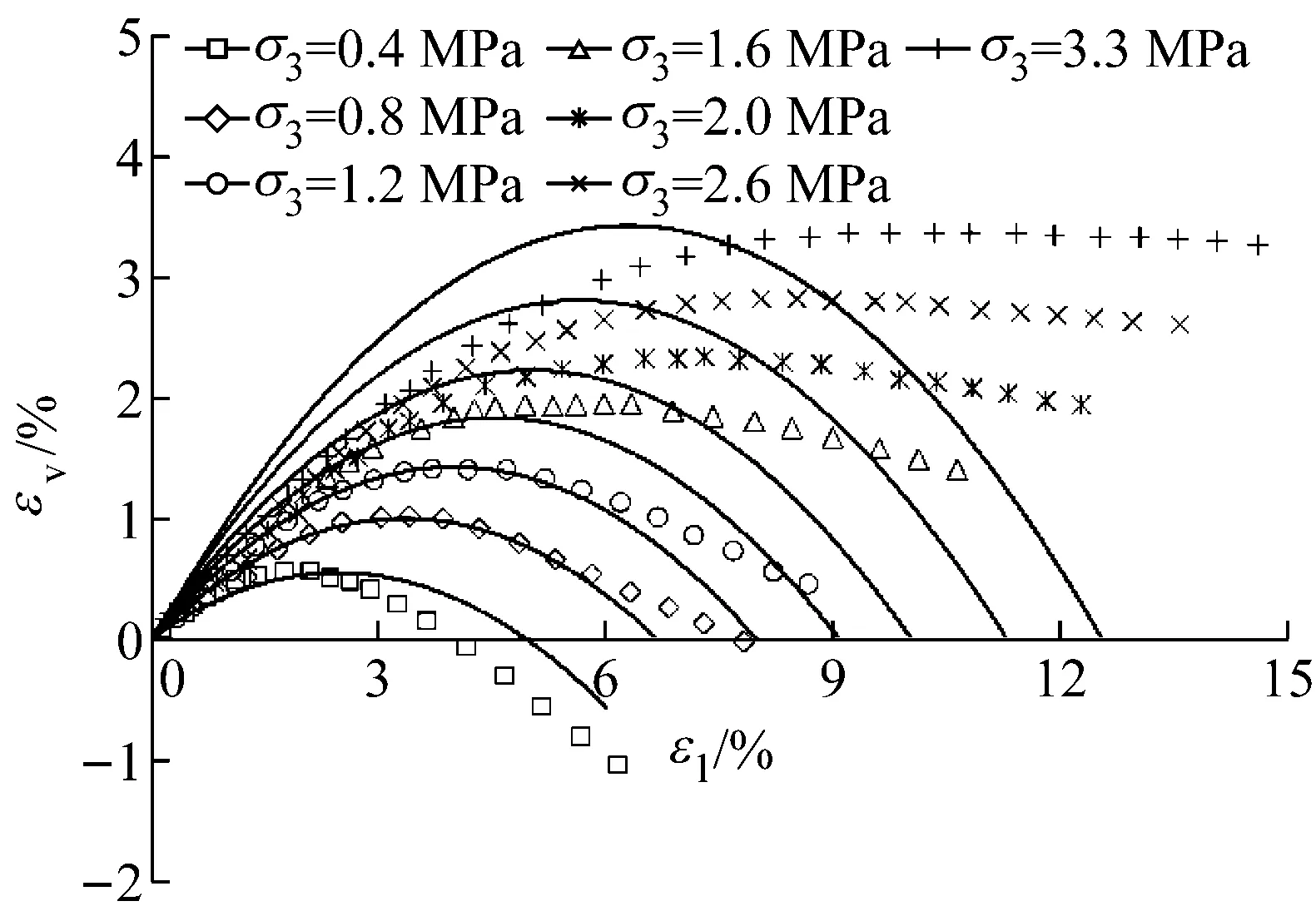
b εv-ε1拟合曲线

2“南水”双屈服面模型的修正

2.1堆石料的轴向应力-应变关系

图3中整理了4种不同围压下堆石料切线模量与应力比的关系，图中横坐标为应力比η与峰值应力比Mf的比值，拟合曲线和方程表达式如图所示.从图中可以看出，初始切线模量Ei与围压σ3相关，围压越大，初始模量越大，此处仍采用以下公式[7]：

(8)

式中:K和n是两个参数，可根据不同围压的试验值求出.

a 400 kPa

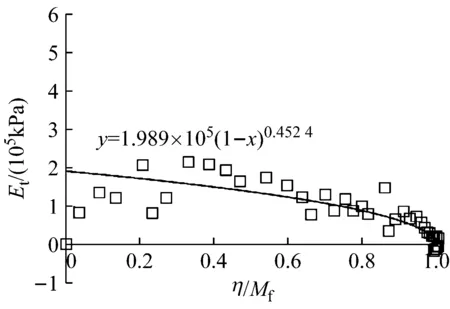
b 800 kPa

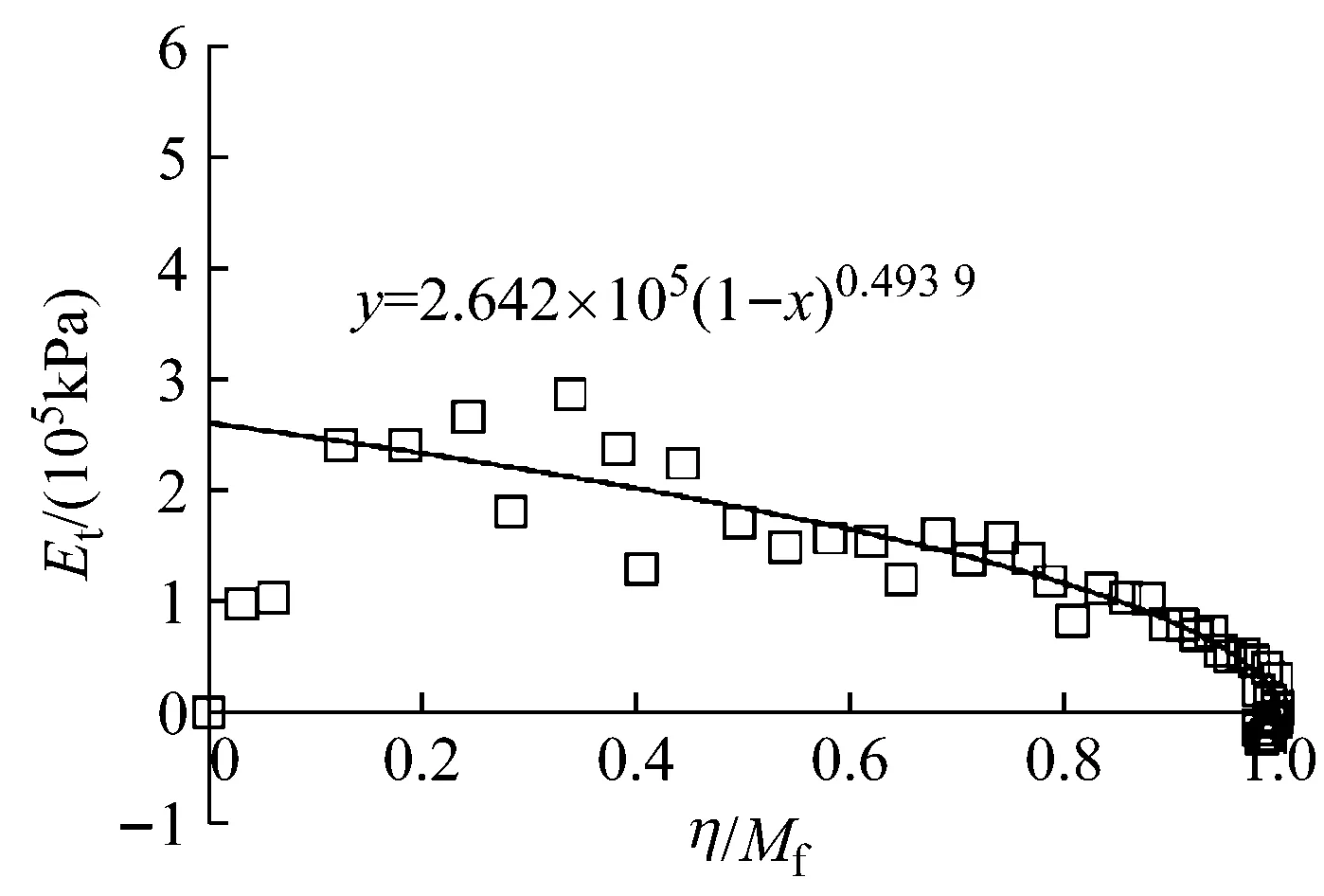
c 1 200 kPa下Et与η的关系

d 3 000 kPa下Et与η的关系

加载过程中，随着应力比η(η=q/p)的增加，切线模量Et逐渐衰减.在η达到峰值应力比后，Et最终趋于0.本文采用式(7)描述切线模量Et的变化规律：

(9)

式中:α为量纲一参数；Mf为峰值应力比，确定如下：

(10)

式中，φf为峰值摩擦角，用来描述堆石料的强度非线性特性，由式(2)计算确定[8].

显然，η=Mf时，切线模量Et=0.此时，在不施加轴向应力的情况下，轴向应变持续发展，达到破坏状态.

2.2堆石料的体变特性

图4中绘制了4种堆石料在不同围压下切线体积比与应力比的关系.图中横坐标为应力比η与某一临界状态应力比Mc的比值，拟合曲线和方程表达式如图4所示.

从图中可以看出，在初始加载阶段，切线体积比μt很快地发展到最大值，然后随着应力比η的增加，μt逐渐减小，而大部分点都位于μt的减小区.需要指出的是，在最初加载发生的一瞬，试样实际上是有体变发生的，至于一开始μt值为零，是由于试验中排水管道过长，水未来得及排出，体积变化发生滞后所致.

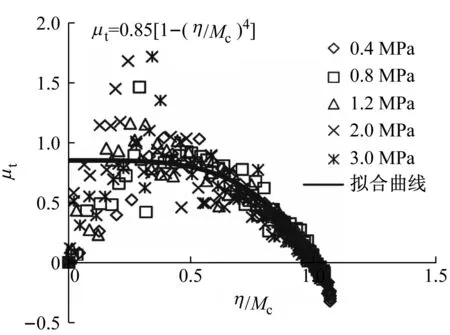
a 堆石料I

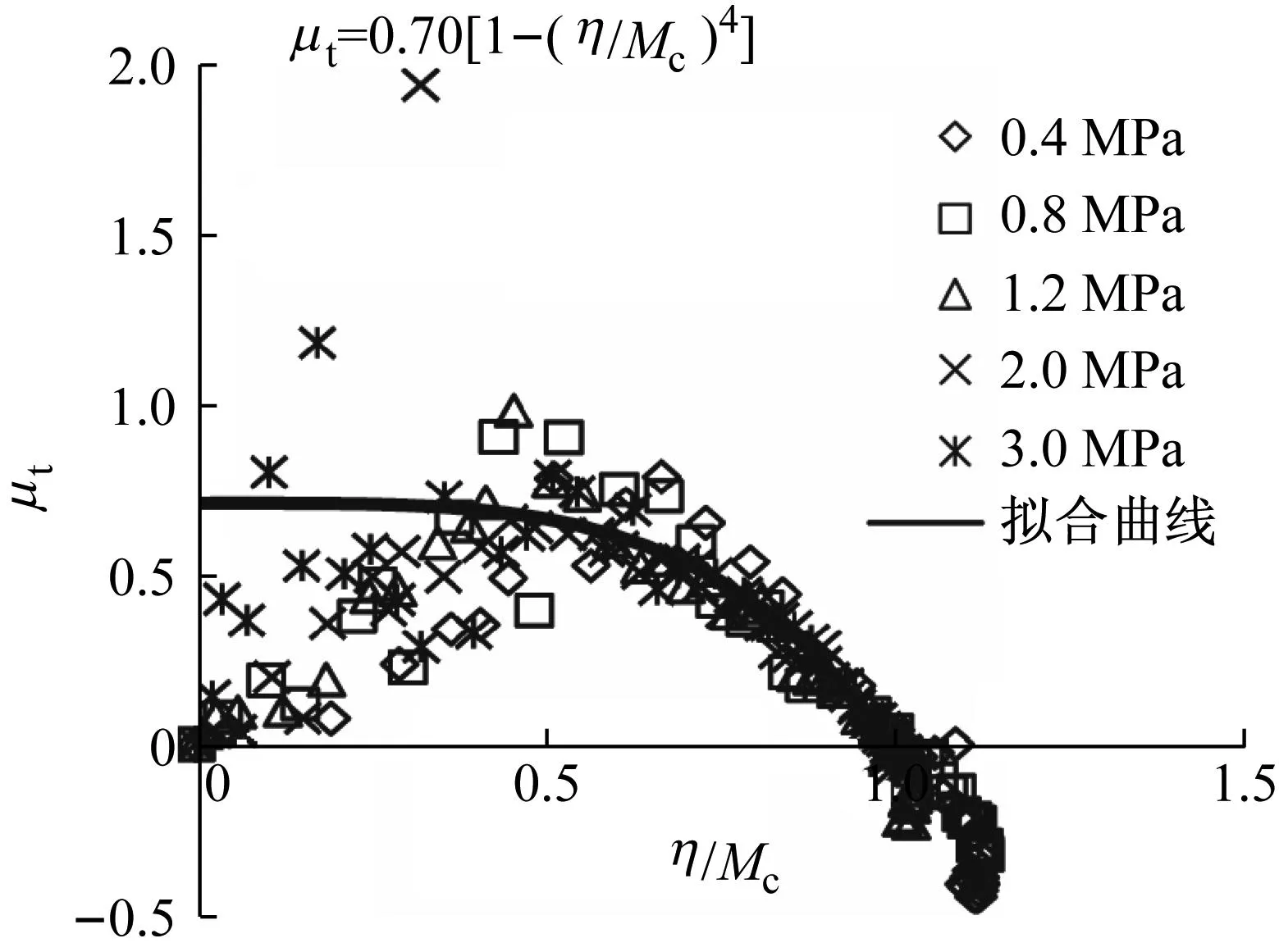
b 堆石料II

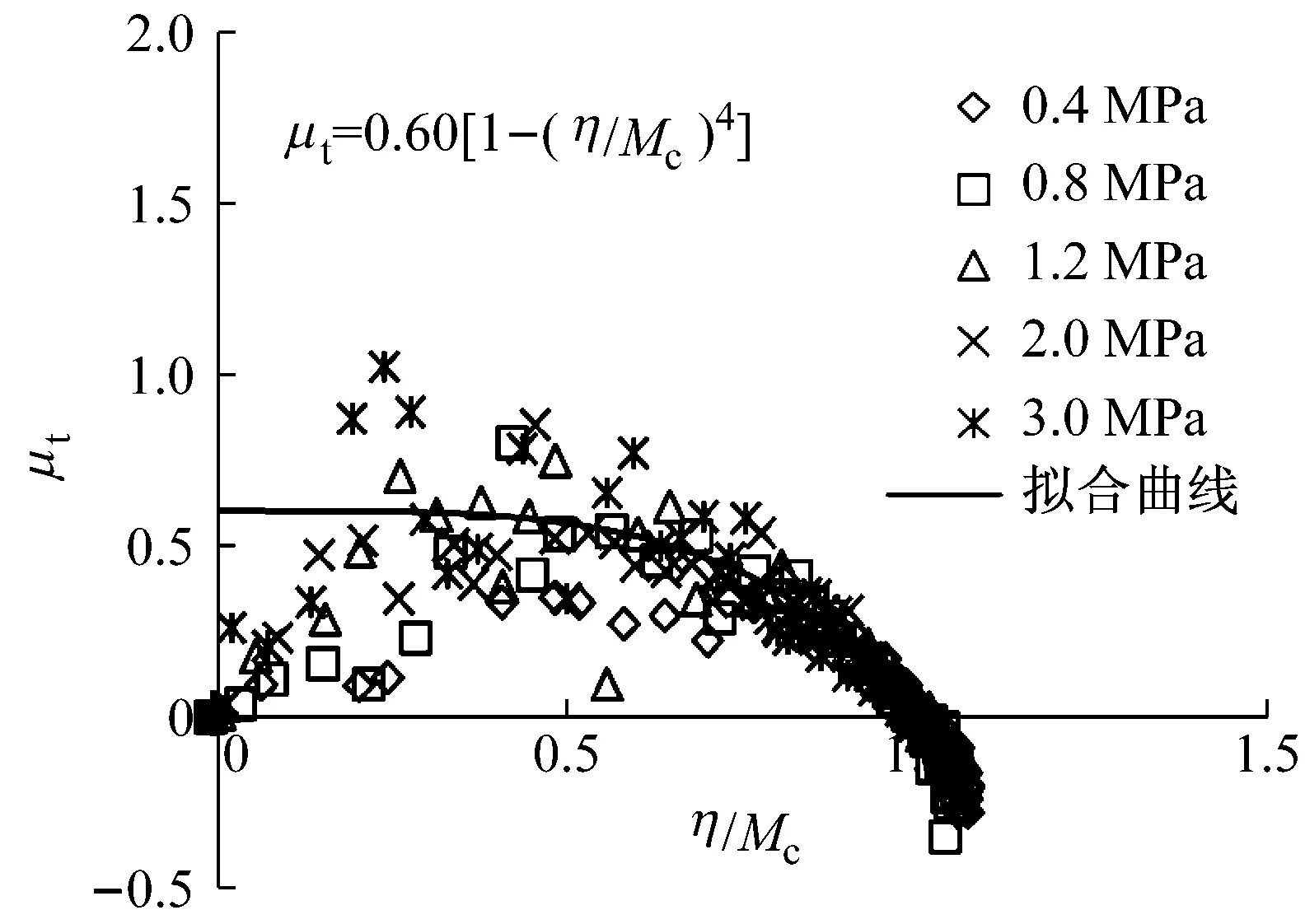
c 堆石料III

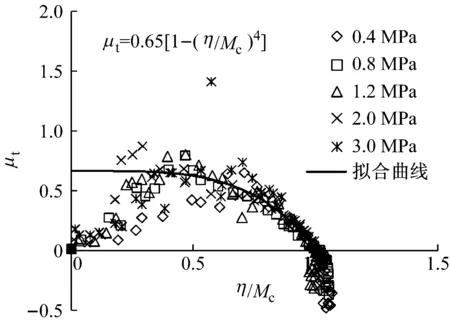
d 堆石料IV

基于上述分析，本文采用式(11)描述切线体积比μt随应力比η的变化：

(11)

式中：μt0为初始切线体积比；Mc定义为临胀应力比，由式(12)确定：

(12)

式中，ψc为临胀摩擦角，用来描述堆石料的剪胀(缩)性与围压σ3之间的非线性关系，即：

(13)

式中：pa为标准大气压，101 kPa；ψ0为围压σ3为大气压力pa时的剪胀摩擦角；Δψ为围压σ3增加一个数量级时剪胀摩擦角降低的幅度.

显然，三轴试验条件下，初始切线体积比μt0<1.而当η=Mc时，μt=0，此时为体积由剪缩变为剪胀的转折点.剪胀特征点对应的摩擦角称为临胀摩擦角ψc，其对应的应力比即为临胀应力比Mc.

综上所述，“南水”双屈服面模型修正后的两个基本变量切线模量Et和切线体积比μt可以表示为应力比η的函数：

(14)

式中：Mf为峰值应力比；Mc为临胀应力比，μt0为初始切线体积比.修正后，幂次α代替原模型中破坏比Rf参数；μt0、ψ0、Δψ代替原模型中cd、nd、Rd三个参数.

3参数确定与模型验证

3.1参数测定

峰值应力比Mf和临胀应力比Mc分别由峰值摩擦角φf和临胀摩擦角ψc计算确定.峰值摩擦角参数φ0、Δφ由φf～lg(p/pa)关系曲线的截距和斜率确定，剪胀摩擦角参数ψ0、Δψ由ψc与lg(p/pa)关系曲线的截距和斜率确定；参数α通过拟合Et-η曲线确定.与“南水”模型相比，修正后的模型参数个数并未增加，且均可由三轴固结排水剪切试验确定.

3.2不同堆石料的试验验证

将本文建议的切线模量Et和切线体积比μt的表达式引入到南水模型，并对某面板堆石坝两种典型筑坝堆石料的三轴试验进行了模拟.堆石料I岩性为玄武岩，属坚硬岩；堆石料II岩性为灰岩，岩石坚硬，呈弱风化较完整状态.表2为相应的模型计算参数，图5和图6中对比了两种材料的试验和模拟结果.从图中可以看出，通过修改切线模量表达式，修正模型较好地反映了堆石料在不同围压下的破坏情况，即应力不变时应变的无限发展；通过修改切线体积比表达式，修正模型能够较好地反映堆石料的初始剪缩，且克服了原始模型后期剪胀过大的缺点.临胀应力比相关的两个摩擦角参数的引入能够合理地反映堆石料低围压下剪胀，高围压下剪缩的特点.

表2　三轴试验修正模型计算参数

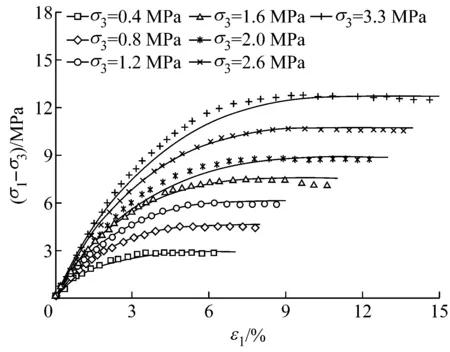
a 堆石料Ⅰ，(σ1-σ3)-ε1

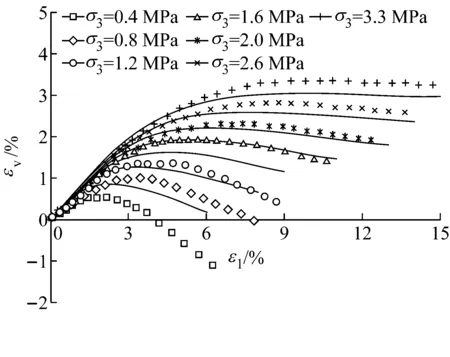
b 堆石料Ⅰ，εv-ε1

3.3不同应力路径的试验验证

为验证修正模型的适用性，对某高心墙堆石坝主堆石料弱风化花岗岩3种不同应力路径下的试验进行了模拟.三种应力路径分别为三轴压缩试验(k=dσ3/dσ1=0)、等p加载(k=-0.5)和等比例加载(k=0.4).每种应力路径都进行了一个卸载和再加载的循环.常规三轴在轴向应变达到15%时进行卸载再加载；等p试验在即将达到破坏强度时，按原路径卸载至q=0，再保持p不变，增大q，加载至试样破坏；等应力比试验在围压力达到1.6 MPa时进行一个卸载和再加载的循环，再加载到围压至2.5 MPa时结束试验[9].根据室内常规三轴排水剪切试验确定了该堆石料的本构模型参数，见表3.本文只模拟单调加载的情况，模拟结果与试验结果的对比见图7-9.

由图7—9可以看出：(1)k<0时，低围压下堆石料很快产生剪胀，剪缩过程较短，随着围压的增大，剪胀程度逐渐减弱直至只有剪缩发生.修正“南水”模型较好地反映了堆石料这一剪胀(缩)规律；(2)k>0时，模型预测的体积变形与轴向变形基本呈线性

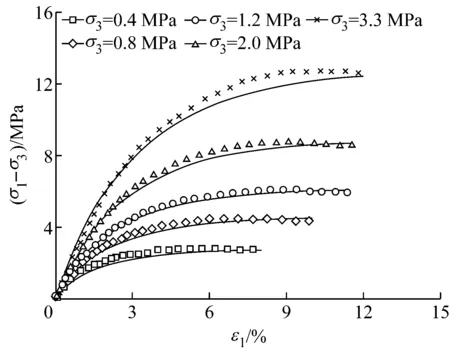
a 堆石料Ⅱ，(σ1-σ3)-ε1

b 堆石料Ⅱ，εv-ε1

材料φ0/(°)Δφ/(°)ψ0/(°)Δψ/(°)μt0KKurnα堆石料III49.49.047.27.10.95710.01420.00.250.8

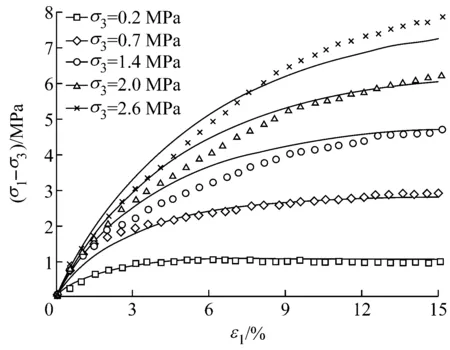
a k=0，(σ1-σ3)-ε1

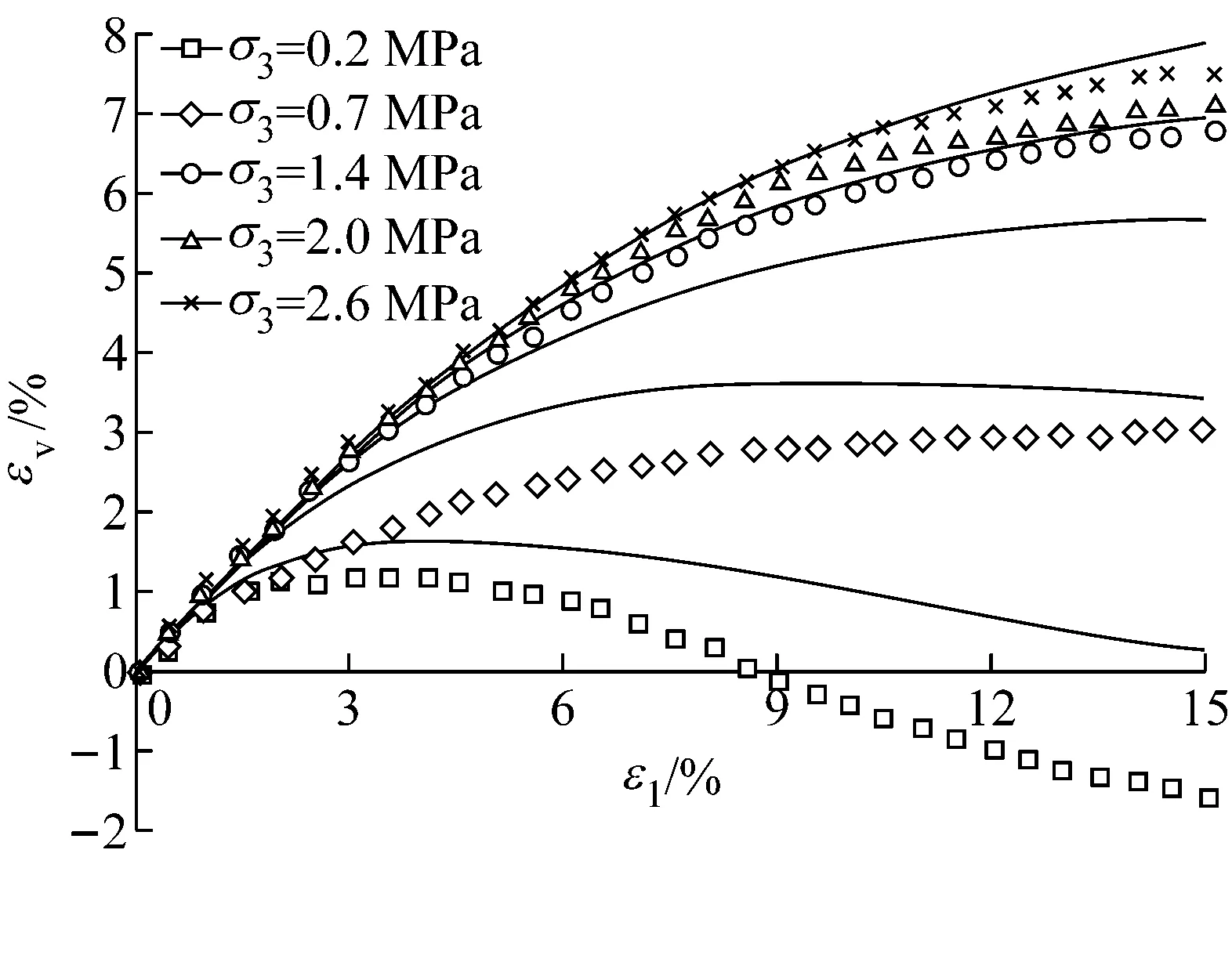
b k=0，εv-ε1

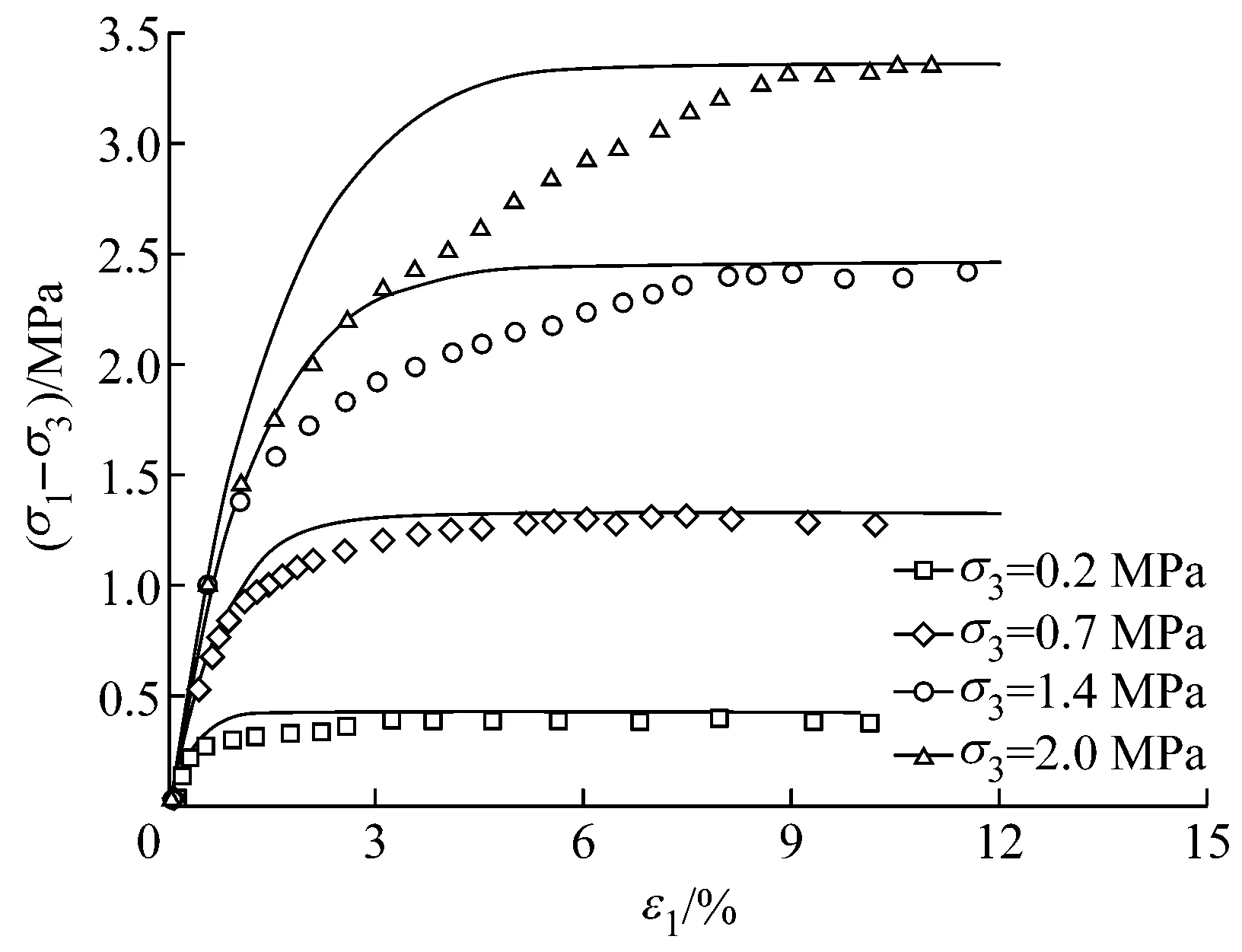
a k=-0.5，(σ1-σ3)-ε1

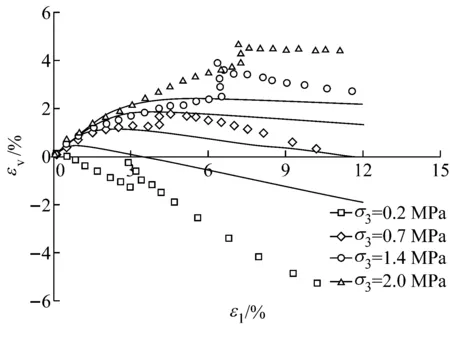
b k=-0.5，εv-ε1

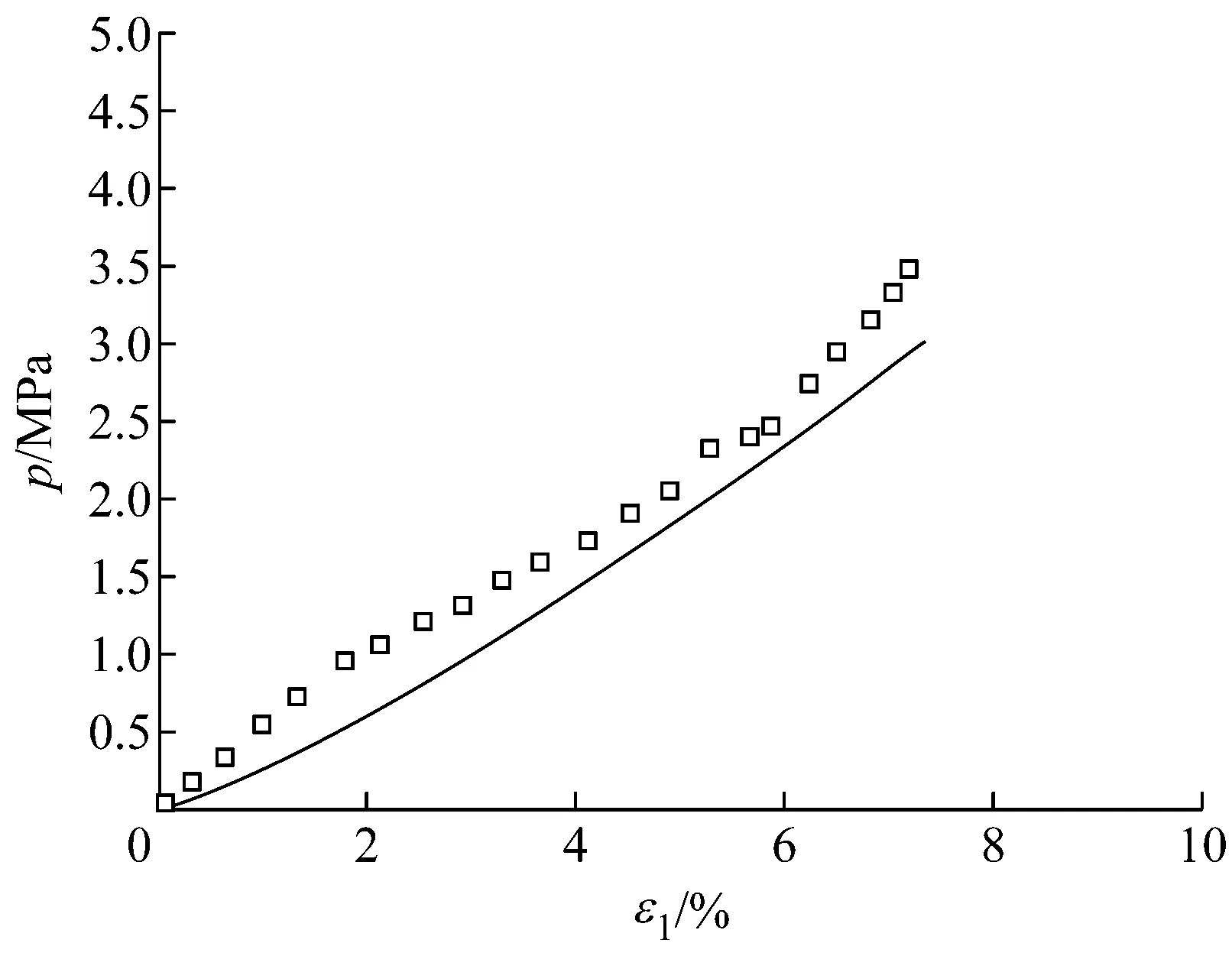
a k=0.4，p-εv

b k=0.4，εv-ε1

关系，在应变较小时与试验结果吻合良好，但当应变较大时，模型预测结果与试验结果差异增加.但总体而言，修正模型可以较好地预测不同应力路径下堆石料的应力-应变关系.

4结论

通过分析三轴压缩试验结果，分别建立了切线模量Et和切线体积比μt与应力比η的关系表达式，并将其引入南水双屈服面模型中，修正了“南水”双屈服面模型在反映堆石料破坏和剪胀(缩)变化规律方面的不足.修正后的“南水”模型具有下述3个特点：

(1)模型在切线模量中未使用破坏比参数，修正后切模量最终趋于0，较好地反映了堆石料在达到峰值应力后保持不变，应变持续发展的破坏特点；

(2)在切线体积比中引入临胀应力比Mc，通过剪胀摩擦角ψc较好地反映了堆石料在低围压下剪胀，高围压下剪缩的剪胀(缩)的变化规律；

(3)修正“南水”模型未增加试验参数，且各参数均可由室内常规三轴试验确定.

运用不同堆石料，多种围压和应力路径下的试验结果对修正“南水”模型进行了验证，表明其可更好地反映堆石料的强度和剪胀(缩)特性.

参考文献:

[1]秦红玉, 刘汉龙, 高玉峰, 等. 粗粒料强度和变形的大型三轴试验研究[J]. 岩土力学, 2004, 25(10): 1575.

QIN Hongyu, LIU Hanlong, GAO Yufeng,etal. Research on strength and deformation behavior of coarge aggregates based on large-scale triaxialtests[J]. Rock and Soil Mechnics, 2004, 25(10): 1575.

[2]Duncan J M, Chang C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(5), 1629.

[3]沈珠江. 土体应力应变分析的一种新模型[C]∥第五届土力学及基础工程学术讨论会论文集. 北京: 中国建筑工业出版社，1990: 101-105.

SHEN Zhujiang. A new constitutive model for soils[C]∥Proceedings of the 5th Chinese Conference on Soil Mechanics and Foundation Engineering. Beijing: China Architechure & Building Press, 1990: 101-105.

[4]张丙印, 贾延安, 张宗亮. 堆石体修正Rowe剪胀方程与南水模型[J]. 岩土工程学报, 2007, 29(10): 1443.

ZHANG Bingyin, JIA Yanan, ZHANG Zongliang. Modified Rowe’s dilatancy law of rockfill and Shen Zhujiang’s double yield surfaces elastoplasticmodel[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(10): 1443.

[5]米占宽, 李国英, 陈生水. 基于破碎能耗的粗颗粒料本构模型[J]. 岩土工程学报, 2012, 34(10): 1801.

MI Zhankuan, LI Guoying, CHEN Shengshui. Constitutive model for coarse granular materials based on breakage energy[J]. Chinese Journal of Geotechnical Engineering,2012, 34(10): 1801.

[6]朱百里, 沈珠江. 计算土力学[M]. 上海:上海科学技术出版社, 1990.

ZHU Baili, SHEN Zhujiang. Computational soil mechanics[M]. Shanghai:Shanghai science and Technology Press, 1990.

[7]Janbu N. Soil compressibility as determined by oedometer and triaxial tests[C]∥Proeeding of the European Confence on Soil Mechanics and Foundation Engineering. Essen: Deutsche Gesellschaft für Erd-und Grundbau. e. V., 1963: 259-263.

[8]陈生水, 傅中志, 韩华强, 等. 一个考虑颗粒破碎的堆石料弹塑性本构模型[J]. 岩土工程学报, 2011, 33(10): 1489.

CHEN Shengshui, FU Zhongzhi, HAN Huaqiang,etal. An elastoplastic model for rockfill materials considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1489.

[9]杨光, 孙逊, 于玉贞, 等. 不同应力路径下粗粒料力学特性试验研究[J]. 岩土力学, 2010, 31(4): 1118.

YANG Guang, SUN Xun, YU Yuzheng,etal. Experimental study of mechanical behavior of a coarse-grained material under various stress paths[J]. Rock and Soil Mechanics, 2010, 31(4): 1118.

Two Modifications to the Shen Zhujiang's Double Yield Surface Model

WANG Tingbo1,2, CHEN Shengshui2,3, FU Zhongzhi2,3

(1. College of Civil Engineering, Tongji University, Shanghai 20092, China; 2.Geotechnical Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210029, China; 3. Key Laboratory of Earth-Rock Dam Failure Mechanism and Safety Control Techniques, Ministry of Water Resources, Nanjing 210024， China)

Abstract：Taking the original triaxial test data as the basis, this study analyzed the relationship between the tangential modulus, or the tangent bulk ratio and the stress state. The corresponding relational expression were proposed, respectively. Then, the two new expressions were introduced into Shen’s elastoplastic model with double yield surfaces to replace the old ones. The triaxial simulated results of rockfill materials showed that the modified model can overcome the disadvantages of using the damage stress ratio to control the final strength, especially the inadequate characteristics of shear dilatation (contraction). And the simulated results of different stress-path triaxial tests confirmed the new model can well simulate the strength and deformation characteristics of rockfill.

Key words：double yield surfaces; elastoplastic model; tangential modulus; tangent bulk ratio; rockfill

文献标志码：A

中图分类号：TU43

通讯作者：陈生水(1962-)，男，工学博士，教授级高级工程师，博士生导师，主要研究方向为土石坝工程.E-mail:sschen@nhri.cn

基金项目：国家自然科学基金(91215301，51379130)；中央级公益性科研院所基本科研业务费专项资金项目(Y314011，Y315005)

收稿日期：2015-04-14

第一作者： 王庭博(1987-)，男，博士生，主要研究方向为高土石坝工程.E-mail:1310176@tongji.edu.cn