热膨胀系数对早期混凝土性态影响试验及数值模拟

崔　溦， 冀天竹， 吴甲一

(天津大学 水利工程仿真与安全国家重点实验室， 天津 300072)



热膨胀系数对早期混凝土性态影响试验及数值模拟

崔溦， 冀天竹， 吴甲一

(天津大学 水利工程仿真与安全国家重点实验室， 天津 300072)

摘要：为了更加准确地计算温度应变，对早期混凝土热膨胀系数的变化规律进行了研究.通过试验得出了早期混凝土温度及应变的变化规律，同时基于ABAQUS二次开发平台，开发出了基于水化度的混凝土温度及应变计算子程序，并在此基础上采用不同的热膨胀系数变化模型对试验进行数值模拟.模拟结果表明，不同的热膨胀系数变化模型对试验的模拟结果不尽相同，其中使用指数型下降的热膨胀系数变化规律与试验结果拟合效果更好.

关键词：早期混凝土； 热膨胀系数； 温度应变； 试验； 数值模拟； ABAQUS

影响混凝土早期开裂的主要因素是温度、湿度和自收缩，其中温度被认为是早期开裂的主要影响因素[1].热膨胀系数作为表征温度变形的重要参数，对早期混凝土的开裂模拟有着重要的影响.然而，很多国内外研究者在计算温度应变过程中将热膨胀系数视为常数，完全忽视了早期混凝土热膨胀系数的龄期依存性[2].

近年来，各国研究者对早期混凝土的热膨胀系数相继进行了大量的试验研究，取得了一定成果.其研究[3]普遍认为混凝土的热膨胀系数受很多因素影响，如相对湿度、粗骨料、水灰比、外加剂等，并且随龄期增长呈规律性变化.Jensen[4]在10°C的变温条件下测量早龄期的砂浆与混凝土的热膨胀系数；Kada等[5]设计了使用高灵敏度的应变计测量高强混凝土随龄期变化的热膨胀系数的实验方案；王贤磊[6]通过研制和应用线膨胀系数测定仪来测定早期混凝土的热膨胀系数；黄杰等[7]进行了不同粗骨料混凝土早期热膨胀系数试验来研究热膨胀系数的变化规律.但是，上述试验都没有考虑“滞后变形”对测量数据的影响.所谓“滞后变形”就是试件在温度改变以后需要等待一段时间才能显示出来的体积变化[8].同时，上述试验也没有很好地分离自收缩变形和温度变形[9].鉴于试验手段的局限性，可以采用测量应变，用数值模拟的方法对早期混凝土的热膨胀系数变化规律进行研究.

本文基于ABAQUS二次开发平台，考虑早期混凝土热膨胀系数随龄期的变化，开发了基于水化度的应力场计算子程序.在对试验结果进行修正的基础上，通过模拟对比，研究了热膨胀系数对早期混凝土应变的影响，并对热膨胀系数各种变化规律的适应性进行了分析.

1试验

1.1原材料

试验所用水泥为唐山奥成牌PO42.5普通硅酸盐水泥，重度为31 kN·m-3，细度为350 m2·kg-1，颗粒平均粒径为19.1 μm；细骨料为海砂，Ⅱ区级配，细度模数2.3，密度2.56 g·cm-3；粗骨料为石灰岩碎石颗粒，重度为25.7 kN·m-3，最大颗粒粒径20 mm连续级配.

1.2试验方案

为了能够达到令人满意的试验效果，试件的形状必须满足以下两点要求：(1)方便实验室内工作且易于数值模拟；(2)试件必须能够产生足够的温度和应力梯度用于监测.按照要求，试件的尺寸拟定为600 mm× 300 mm×600 mm，如图1所示.试件外表面包裹一层用以保温的25 mm厚的聚苯泡沫板和起固定作用的10 mm厚的胶合板.

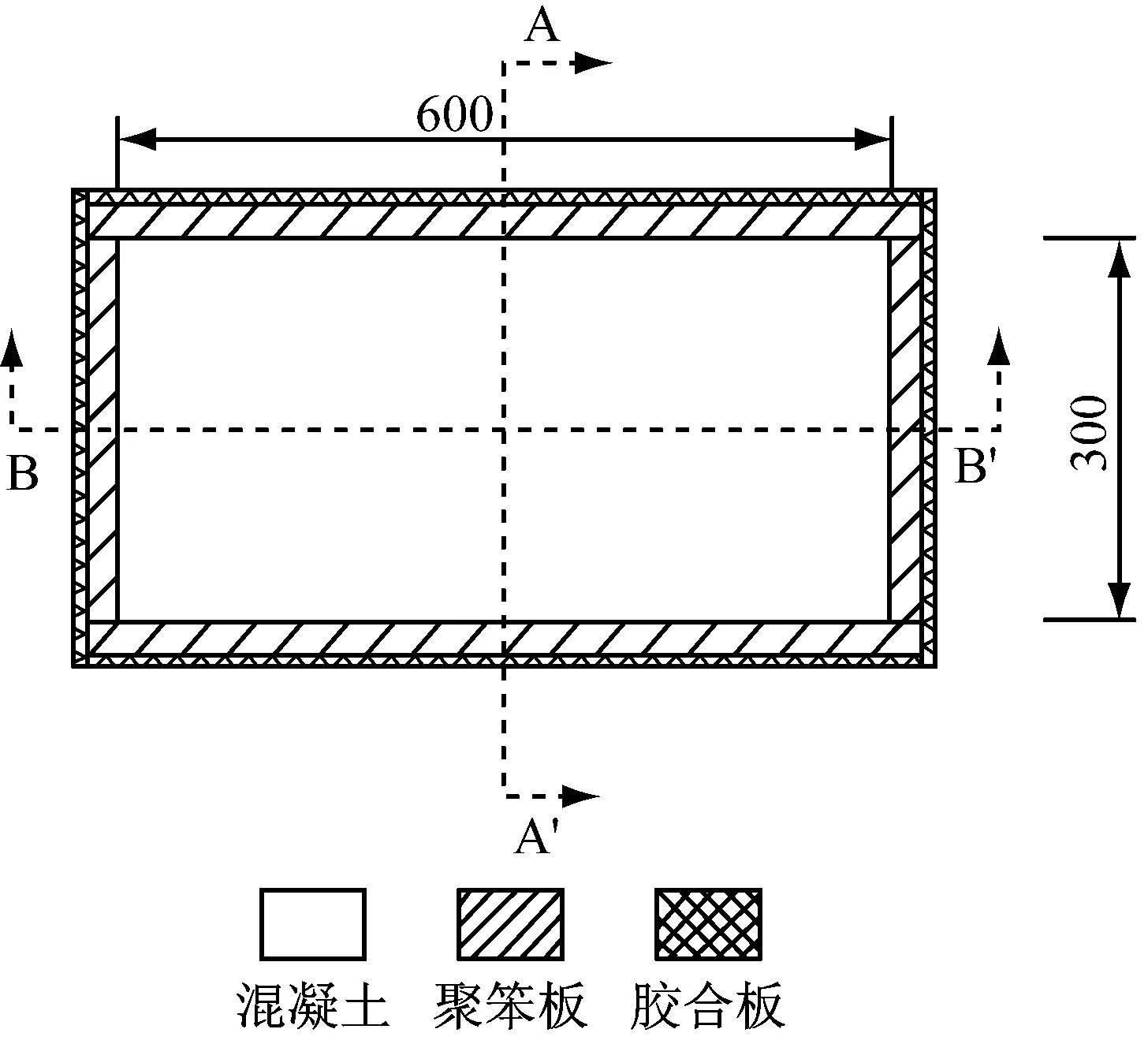
a 平面图

b A-A′剖面图

在混凝土浇筑前，先在浇筑模具内表面接缝处涂抹约2 mm厚的硅胶，然后将聚苯泡沫板贴在模具内表面，聚苯板接缝处密封，后期浇筑完成之后，试件顶部同样用聚苯板密封，起到保温和防止水分蒸发的作用，减小早期混凝土干缩和塑性收缩的影响[7].之后，将两个振弦传感器和三个温度传感器固定在模具内部，具体布置位置详见图1.其中两个振弦传感器被布置在试件的中轴面上不同的高度，一个布置在距顶面200 mm处，此传感器记为VWS-T；另一个布置在距底部200 mm处，记为VWS-B.两个温度传感器分别布置在振弦传感器正下方，用来测量振弦传感器处的温度变化；另外一个温度传感器布置在距顶部300 mm混凝土与聚苯板的交界处，用以验证数值模型的温度边界条件，三个温度传感器从上往下依次记为TS-1、TS-2、TS-3，其实物布置如图2所示.

完成上述准备工作以后，浇筑混凝土试件，按照0.4水灰比配制混凝土，本次试验具体用量如表1所示.将混凝土充分搅拌以后装入模具，同时，根据标准[10]，将混凝土筛分后的砂浆浇入三个金属圆筒，用以判定混凝土的初凝及终凝时间.

a传感器布置概图b试验装置概图

图2试验装置及传感器概图

Fig.2Overview of experimental setup and sensors

表1　各种材料用量

1.3试验结果分析

1.3.1温度

温度传感器测量的混凝土试件温度如图3所示.由温度变化结果可知，受水泥水化反应影响混凝土内部温度经历了一个先增加后减小的变化过程.由图可以看出，TS-1与TS-3温度变化基本一致，尤其是前70 h，后期TS-1温度逐渐低于TS-3；TS-2前期温度变化规律与TS-1、TS-3基本一致，但在具体量值上有一定差别.其中测得的温度峰值TS-1为40.68℃(34.5 h)；TS-2为38.6℃(34.5 h)；TS-3为40.86℃(34 h).其主要原因是TS-3布置于混凝土试件中部，其环境相对更接近于绝热状态，所以前期其温度增长较快并且其温升最高；TS-1测得温度变化规律与TS-3大致相同，后期温度降低速度略大于TS-3的温度降低速度，主要是由于TS-1相较于TS-3更接近顶部，散热效果更好.在图中同样可以看出，混凝土刚浇筑完成就开始了水化温升阶段，一直持续到34 h；其后开始降温阶段，鉴于试验是用以验证适用于早期混凝土的热膨胀系数变化规律，所以数据仅记录到143 h，没有等到混凝土内部温度达到稳定值.

图3　温度传感器测量值

1.3.2应变

按照标准规定[10]，对混凝土的凝结时间进行测量，可得出在养护温度为20.4 ℃的条件下，本次试验初凝时间为7 h 15 min，终凝时间为11 h 30 min.

混凝土试件应变随时间变化的曲线如图4所示.从图中可以看出，应变的变化规律与温度基本一致，即从浇筑完成开始，由于水泥水化放热，混凝土温度升高发生温度膨胀，而此时混凝土仍处于塑性或半塑性状态，其温度上升较为缓慢，混凝土的自收缩占有较大比例.由图可知，混凝土初凝前的应变增长较为缓慢，初凝后随着水化反应的继续，一方面混凝土温升加速，膨胀变形增大，另一方面混凝土的自收缩也不断增加，由于温度增长迅速，因此温度膨胀在总变形中占主导，总变形体现为膨胀变形，内部监测点受到的主要是压应变.之后随着水化反应速率的降低，温升速度也随之降低，自收缩所占比例逐渐增大，应变增长速率开始放缓.在混凝土温度到达峰值之后，受滞后变形的影响，应变随后达到峰值，在35 h时应变均达到了最大值.随着水化反应速率的逐渐降低，混凝土内部温差逐渐降低，压应变也逐渐降低.最终应变会随着温差的消失而趋于稳定.由于VWS-B与VWS-P所测得的应变值结果基本一致，因此下文中仅验证VWS-B测得的应变.

图4　振弦传感器测量值

考虑混凝土初凝前没有形成固体性质的热膨胀系数，混凝土与振弦传感器结合不紧密会导致所测得应变值与实际值有较大差异，因此要对初凝前所得测量值进行修正.通常认为混凝土初凝之前无法形成应变或者应变太小无法测量到[11]，而从实测应变值中剔除初凝前测值才能用以验证数值模拟结果.但是考虑滞后变形对测量数据的影响，完全减掉这部分应变可能会造成较大偏差，因此本文采用实测应变减去初凝之前的应变作为下界，将实测应变作为上界，如果数值模拟结果位于上下界之间，则认为该结果符合实际.根据测得的混凝土初凝时间对应变数据进行修正，如图5所示.

考虑早期混凝土自收缩的影响，由于目前早期混凝土的自收缩还没有统一的标准测量方法，本文参照安明哲等[12]的试验方法，采用位移传感器来自动测试混凝土的早期收缩，混凝土试件尺寸为0.15 m×0.15 m×0.60 m棱柱型试件.试验过程中允许试件的自由变形，并用石蜡将试件与外界空气隔绝，除去湿度的影响.由此得出自收缩应变结果如图6所示.由于数值模拟不能反映混凝土的自收缩变形，因此，需在模拟结果中加上该部分应变，以用于复核试验成果.

图5　应变修正值

图6　混凝土自收缩应变

2数值模拟理论

2.1基于水化度理论的温度应力场模拟

本文的数值模拟采用考虑水化度影响的温度场计算模型，并考虑热学参数随水化度的变化过程[13].

考虑到早期混凝土的粘弹性力学行为，本次计算选用对早期混凝土温度应力有较好模拟的双幂徐变函数(DPL)模型[14].同时为了减少对应力(应变)历史的存储量，在有限元计算过程中，需要将徐变方程展开成泰勒级数形式，同时需要将增量步内的应力增量表达为应变增量和应力(应变)历史的显示表达式.

2.2早期混凝土的热膨胀系数

热膨胀系数是物质在热胀冷缩效应作用下，几何特性随温度变化而发生变化的规律性系数.通常认为混凝土是各向同性材料，所以由温度变化T所引起的混凝土温度变形值如下

(1a)

(1b)

式中：εx、εy、εz为轴向应变；γxy、γyz、γzx为剪切应变；α为平均线膨胀系数，10-6℃-1；T为温度增量，℃.

式(1)中假设早期混凝土的热膨胀系数是常数，而实际上早期混凝土的热膨胀系数是一个随龄期变化的量，其数值变化范围非常大，初凝时热膨胀系数通常是成熟混凝土热膨胀系数的数倍之高.目前，对早期混凝土的热膨胀系数研究非常有限，至今还没有统一的定论.其中主要有两种代表观点：一种是早期混凝土的热膨胀系数在出现最大值之后即迅速下降达到最小值，之后缓慢回升最终保持稳定；另外一种是早期混凝土的热膨胀系数出现最大值之后就迅速下降到最小值并保持稳定.现选取国内外具有代表性的成果进行验证：

Bjontegaard等[15]通过研究得出，混凝土的热膨胀系数在初凝前后具有很高的数值，随后迅速下降并达到最小值，之后又缓慢增大最终保持稳定.

清华大学的张涛[16]通过试验对王贤磊公式进行了优化，得到的公式如下：

(2)

式中：αT(t)为随龄期变化的热膨胀系数；αk为28 d的热膨胀系数；t为龄期，h；m为水化时间参数，常数，普通混凝土与硅灰混凝土(掺量少于10%)m=2.0，粉煤灰混凝土(粉煤灰掺量大于15%)m=1.5.

Jeong等[17]通过一系列实验得出早期混凝土的热膨胀系数的变化规律，即从浇筑之后混凝土的热膨胀系数就迅速下降，并在8 h左右达到最小值，之后又缓慢回升，最终保持稳定.

现选用以上三种研究成果进行验证，其热膨胀系数随龄期变化规律的试验结果如图7所示.选用以上三种成果的原因主要是：一方面以上三种混凝土的热膨胀系数的变化规律具有代表性，基本涵括了目前各种相关研究的类型，另一个方面是以上三种混凝土热膨胀系数变化规律的适用条件基本相同，其规律同样适用于本文实测结果，具有一定可比性.

2.3实现方法

对于早期混凝土温度应力场的模拟需要用到UMATHT、FILM和UMAT三个用户子程序，其中UMATHT子程序用来定义材料的热行为，模拟混凝土的水化放热过程；FILM子程序用来定义热交换和环境温度，定义混凝土与空气接触的第三类边界条件；UMAT子程序用来模拟早期混凝土的本构关系，考虑随龄期变化的热膨胀系数对早期混凝土应变计算的影响，并求得随热膨胀系数变化的温度应变.

图7　混凝土热膨胀系数试验结果

同时，为了更加准确地模拟早期混凝土的变形，将试验得出的自收缩应变作为已知应变增量加入到UMAT子程序中，需要注意的是，在UMAT中应变是随计算迭代逐步更新的，因此所求得的温度应变及试验所得的自收缩应变也要随着迭代步STEP的更新而更新.

3对试验的数值模拟

3.1有限元计算条件

采用ABAQUS软件进行有限元数值模拟，计算模型如图8所示.计算时间为浇筑后143 h(假设一次浇筑完成).混凝土材料参数见表2.

图8　有限元模型

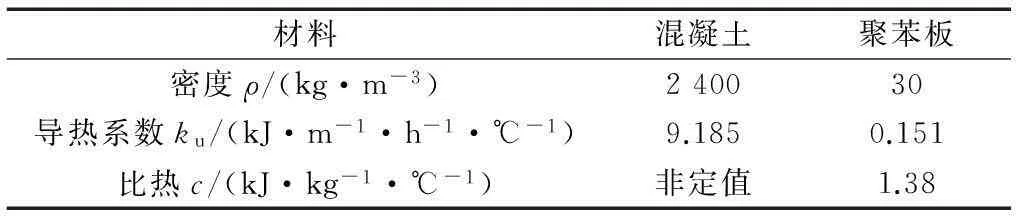
材料混凝土聚苯板密度ρ/(kg·m-3)240030导热系数ku/(kJ·m-1·h-1·℃-1)9.1850.151比热c/(kJ·kg-1·℃-1)非定值1.38

在温度场模拟中，UMATHT子程序定义的混凝土绝热温升方程[18]如下所示：

(3)

式中，θ为考虑水化度的混凝土绝热温升，℃.

由于混凝土试件顶部、底部及侧面具有保温板及模板，因此FILM子程序定义的温度边界条件为第三类边界条件，等效表面散热系数βs计算公式[19]如下：

(4)

式中：βs为等效表面散热系数；β为保温板在空气中的散热系数；hi为保温板厚度，m；λi为保温板的导热系数，kJ·m-1·h-1·℃-1.

根据式(4)，试件顶部热交换系数取为28.8 kJ·m-2·h-1·℃-1，其他边界热交换系数取为15.12 kJ·m-2·h-1·℃-1.由于顶部密封仅仅使用了聚苯板，而四周与底部除聚苯板以外还有胶合板，因此顶部散热较快，热交换系数取值较高.

环境温度变化公式如下所示:

(5)

式中,Ta为随时间变化的环境温度.

在应力场模拟中，对模型底部施加全约束，四周侧面施加法向约束，考虑自重的影响，同时，把温度计算结果做为温度荷载施加到模型上.

计算按以下4种工况分别模拟试验：工况一，采用稳定的热膨胀系数来拟合试验结果；工况二，采用Bjontegaard得出的热膨胀系数变化规律来拟合试验结果；工况三，采用清华总结得出的热膨胀系数变化规律来拟合试验结果；工况四，采用Jeong得出的热膨胀系数变化规律来拟合试验结果.

3.2有限元结果与分析

3.2.1温度

试件数值模拟的温度场计算结果要与试验结果作对比.图9展示的是温度最高时刻(34 h)时温度场分布状况.同时，为了验证数值模拟的准确性，将数值模拟试件上监测点处的温度变化与试验结果相对比，如图10所示.

从图9可以看出，混凝土试件顶部温度较低，主要原因是顶部的热交换系数较大其散热较快，所以顶部温度较低，且呈越靠近底部温度越高的趋势.从图10中可以看出3个监测点处模拟的温度变化规律与试验结果大体相同，仅在34 h温度最高时相差1°C左右，因此可把结果用于结构场模拟.

图9　34 h温度数值模拟结果

图10　混凝土试件温度对比

3.2.2应变

图11给出了工况一条件下数值模拟得出的应变变化规律与试验结果的对比.由图可见，采用常量热膨胀系数得出的应变结果与实测结果在变化规律上基本一致，但前期应变变化较缓，后期相近.在具体量值上则差别较大，尤其是前100 h应变值，峰值应变与下限峰值应变差值达50×10-6以上，后期应变差值渐趋于稳定.

图12—14分别给出了工况二、工况三、工况四条件下进行数值模拟得出的应变变化规律与试验结果的对比.

从图12中可以看出，采用Bjontegaard总结的热膨胀系数变化规律得出的应变结果与实测结果在变化规律上基本一致，但其前期应变变化较缓，在具体量值上则差别较大，尤其是前100 h应变值，同一时刻前期应变值与下限应变差值最大达90×10-6以上，后期差异逐渐减小.

从图13中可以看出，采用清华大学总结的热膨胀系数变化规律得出的应变结果与实测结果在变化规律上基本一致，但其初凝前应变变化较缓，在具体量值上也差别不大，其应变变化曲线基本处于上下限之间，后期差异逐渐增大.

从图14中可以看出，采用Jeong总结的热膨胀系数变化规律得出的应变结果与实测结果在变化规律和具体量值上基本一致，其应变变化曲线基本处于上下界曲线之间.

图11　工况一条件下应变模拟对比

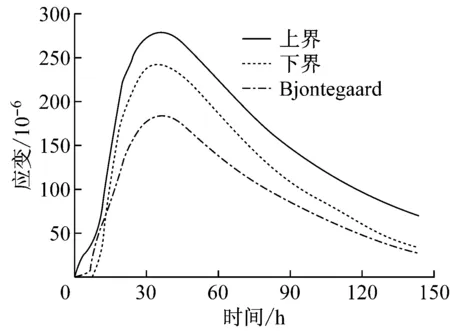
图12　工况二条件下应变模拟对比

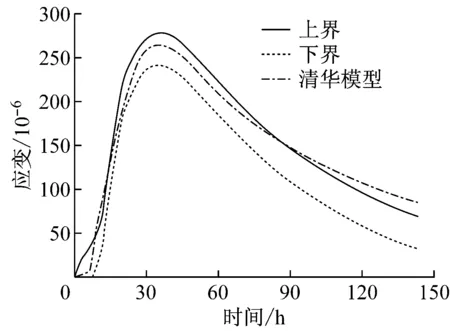
图13　工况三条件下应变模拟对比

3.2.3结果分析

当不考虑热膨胀系数变化时，数值模拟结果与实测值存在较大误差，从图11中可以看出，当采用常量热膨胀系数进行数值模拟时与实测结果在具体量值上差别很大.三种热膨胀系数变化规律得出的应变结果与实测结果在变化规律上基本一致，但是在具体量值上则差别较大.Bjontegaard得出变化规律拟合应变结果与实测结果相差较大，低于下限应变值；清华模型与Jeong总结的变化规律拟合的应变结果则与实测结果拟合较好，基本处于上下限曲线之间.可见，对于普通混凝土而言，指数型下降的热膨胀系数变化规律更能反映混凝土的早期性态，而采用先降到最小而后略有增加的热膨胀系数变化规律所得结果则明显小于实测结果，这与文献[20]结论一致.从图12—13可看出由于不考虑初凝前的热膨胀系数变化，即忽略初凝前的温度应变，仅考虑混凝土的自生收缩，从而导致清华模型、Bjontegaard得出前期应变值较小.因此，在进行早期混凝土应力计算时有必要考虑初凝前的温度应变.

图14　工况四条件下应变模拟对比

4结论

(1)基于ABAQUS二次开发平台，开发了能够真实合理模拟早期混凝土温度场的用户子程序UMATHT和FILM及热膨胀系数随龄期变化的应力场子程序UMAT，并通过算例验证了子程序开发的合理性.

(2)本文采用不同的热膨胀系数变化规律对试验结果进行数值模拟，模拟结果表明：采用不同的热膨胀系数变化规律模型对早期混凝土温度应变的发展规律没有显著影响，但是对温度应变具体数值的大小有较大影响.其中在本试验范围内使用指数型下降的热膨胀系数变化规律与试验结果拟合效果更好，尤其是有考虑初凝前的热膨胀系数变化的Jeong模型.由此可知，初凝前温度应变对最终应变有一定影响，在研究早期混凝土应力变化时不应完全忽略.

(3)从对试验结果的拟合分析可知，当不考虑热膨胀系数变化时，数值模拟结果与实测值存在较大误差，尤其是是在量值上远低于实测值.由此可知对早期混凝土的应力场分析时不考虑热膨胀系数的变化会导致对应力峰值的预测偏低，从而导致不合理的抗拉设计.

参考文献:

[1]Yeon J H, Choi S, Won M C. In situ measurement of coefficient of thermal expansion in hardening concrete and its effect on thermal stress development [J]. Construction and Building Materials, 2013, 38: 306.

[2]江晨辉，杨杨，李鹏,等. 水泥砂浆的早龄期热膨胀系数的时变特征[J]. 硅酸盐学报，2013，41(5)：605.

JIANG Chenhui, YANG Yang, LI Peng,etal. Time dependence on thermal expansion behavior of cement mortar at early ages [J]. Journal of the Chinese Ceramic Society, 2013, 41(5): 605.

[3]沈德建，申嘉鑫，黄杰,等. 早龄期及硬化阶段水泥基材料热膨胀系数研究[J]. 水利学报，2012，43(增)：153.

SHEN Dejian, SHEN Jiaxin, HUANG Jie,etal. Research on current for determining coefficient of thermal expansion of cement based materials at early ages and in hardening stage[J]. Journal of Hydraulic Engineering, 2012, 43(Supplement): 153.

[4]Jensen O M, Hansen P F. Influence of temperature on autogenous deformation and relative humidity change in hardening cement paste [J]. Cement and Concrete Research, 1999, 29(4): 567.

[5]Kada H, Lachemi M， Petrov N,etal. Determination of the coefficient of thermal expansion of high performance concrete initial setting [J]. Material and Structures. 2002, 35: 35.

[6]王贤磊. 混凝土温度线膨胀系数测定仪的研制与应用[D]. 北京：清华大学，2005.

WANG Xianlei. Development and application of the test machine for linear thermal expansion coefficient of concrete [D]. Beijing: Tsinghua University, 2005.

[7]黄杰，吴胜兴，沈德建. 不同粗骨料混凝土早期热膨胀系数试验研究[J]. 结构工程师, 2010，26(3)：154.

HUANG Jie, WU Shengxing, SHEN Dejian. Experimental study on thermal expansion coefficient of different type coarse aggregates concrete at early ages [J]. Structural Engineers, 2010, 26(3): 154.

[8]危鼎. 水泥基材料早龄期热膨胀系数试验研究与理论分析[D]. 南京：河海大学，2007.

WEI Ding. Experimental study and theoretical analysis on the thermal expansion coefficient of cement-based material at early-age [D]. Nanjing: Hehai University, 2007.

[9]Viviani M, Glisic B, Smith I F C. Separation of thermal and autogenous deformation at varying temperatures using optical fiber sensors [J]. Cement and Concrete Composites, 2007, 29(6): 435.

[10]中华人民共和国建设部.GB/T(50080)—2002 普通混凝土拌合物性能试验方法标准[S]. 北京：中国建筑工业出版社，2003.ChinaMinistryofConstruction.GB/T(50080)—2002Standardfortestmethodofperformanceonordinaryfreshconcrete[S].Beijing:ChinaArchitecture&BuildingPress,2003.

[11]李飞. 混凝土早期约束应力发展与松弛过程研究[D]. 北京：清华大学，2009.

LI Fei. Research on the development of restraint stress and relaxation of concrete at early age [D]. Beijing: Tsinghua University, 2009.

[12]安明哲，覃维祖，朱金铨. 高强混凝土的自收缩试验研究[J]. 山东建材学院学报，1998(增1)：139.

AN Mingzhe, TAN Weizu, ZHU Jinquan. Experimental study on autogenous shrinkage of high-strength concrete [J]. Journal of Shandong Institute of Building Materials, 1998(Supplement 1): 139.

[13]Ilc A, Turk G, Kavcic F,etal. New numerical procedure for the prediction of temperature development in early age concrete structures [J]. Automation in Construction, 2009, 18(6): 849.

[14]Atrushi D. Tensile and compressive creep of early age concrete: testing and modeling [D]. Trondheim: Norwegian University of Science and Technology, 2003.

[15]Bjontegaard O, Sellevold E. Interaction between thermal dilation and autogenous deformation in high performance concrete [J]. Materials and Structures, 2001, 34(5): 266.

[16]张涛，混凝土早期开裂敏感性的影响因素研究[D]. 北京：清华大学，2006.

ZHANG Tao, Studies on influencing factors of cracking sensitivity of concrete at early ages [D]. Beijing: Tsinghua University, 2006.

[17]Jeong J H, Dan G Z, Lim J S,etal. Age and moisture effects on thermal expansion of concrete pavement slabs [J]. Journal of Materials In Civil Engineering, 2012, 24(1): 8.

[18]崔溦，陈王，王宁. 早期混凝土热学参数优化及温度场精确模拟[J]. 四川大学学报：工程科学版，2014，46(3)：161．

CUI Wei, CHEN Wang, WANG Ning. Early concrete thermal parameters optimization and accurate thermal field simulation [J]. Journal of Sichuan University: Engineering Science Edition, 2014, 46(3): 161.

[19]朱伯芳. 大体积混凝土的温度应力与温度控制[M]. 北京：中国水利水电出版社，1999.

ZHU Bofang. Thermal stresses and temperature control of mass concrete [M]. Beijing: China Water & Power Press, 1999.

[20]Azenha M, Rui F, Ferreira D. Identification of early-age concrete temperature and strains: Monitoring and numerical simulation[J]. Cement & concrete composites, 2009, 31(6): 369.

Experimental Study and Numerical Simulation for the Effect of Thermal Expansion Coefficient on the Behavior of Early Concrete

CUI Wei, JI Tianzhu, WU Jiayi

(State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University，Tianjin 300072，China)

Abstract：For the more accurate calculation of thermal strain, the change law of the thermal expansion coefficient of early concrete is studied. The change law of early concrete temperature and strain is obtained through the experiment. At the same time, the user subroutine, which to calculate concrete temperature and strain considering hydration degree theory, has been developed based on ABAQUS secondary development platform. And on this basis, The change models of different thermal expansion coefficients are used to simulate the experiment. The numerical simulation results show that simulation results with different thermal expansion coefficient change models are not the same. While the exponential decline change model of the thermal expansion coefficient fits the experimental results better.

Key words：early concrete; thermal expansion coefficient; temperature strain; experiment; numerical simulation; ABAQUS

文献标志码：A

中图分类号：TU528

基金项目：国家自然科学基金创新研究群体科学基金(51021004)；国家自然科学基金(51279126)；天津市自然科学基金(13JCQNJC06800)

收稿日期：2015-04-10

第一作者： 崔溦(1977—)，男，工学博士，副教授，主要研究方向为岩土工程稳定性及早期混凝土性态.E-mail：cuiwei@tju.edu.cn