基于多观测向量的高光谱影像稀疏表达分类

孙伟伟，　刘　春，　李巍岳

(1. 武汉大学 测绘遥感信息工程国家重点实验室， 湖北 武汉 430079;

2. 宁波大学 建筑工程与环境学院， 浙江 宁波 315211; 3. 同济大学 测绘与地理信息学院， 上海 200092;

4. 现代工程测量国家测绘地理信息局重点实验室， 上海 200092; 5. 上海师范大学 城市发展研究院， 上海 200234;

6. 矿山空间信息技术国家测绘地理信息局重点实验室， 河南 焦作 454000)



基于多观测向量的高光谱影像稀疏表达分类

孙伟伟1,2，刘春3,4，李巍岳5,6

(1. 武汉大学 测绘遥感信息工程国家重点实验室， 湖北 武汉 430079;

2. 宁波大学 建筑工程与环境学院， 浙江 宁波 315211; 3. 同济大学 测绘与地理信息学院， 上海 200092;

4. 现代工程测量国家测绘地理信息局重点实验室， 上海 200092; 5. 上海师范大学 城市发展研究院， 上海 200234;

6. 矿山空间信息技术国家测绘地理信息局重点实验室， 河南 焦作 454000)

摘要：针对传统的高光谱影像稀疏表达分类模型忽略像元间的内部结构关系且运算效率较低，提出多观测向量的稀疏表达模型来研究高光谱影像分类.该模型引入平衡参数来控制各权重系数向量的稀疏度，通过最小化L2范数约束的重构误差来求解所有测试像元的稀疏系数向量.基于两个高光谱数据集，对比5种常规分类器的分类结果来验证提出的方法.实验结果表明，多观测向量的稀疏表达分类模型在计算效率第二的同时能够得到最高分类精度.

关键词：多观测向量； 稀疏表达； 高光谱影像； 分类

高光谱遥感技术利用成像光谱仪能够获得地物在一定波段区间内的光谱响应曲线[1].不同地物在特定波段范围内的光谱响应特征不同，因此可以利用高光谱影像分类来识别不同地物间的细微差异.高光谱影像的分类结果对植被覆盖制图[2]、海洋环境监测[3]和资源勘查[4]等具有重要作用.

近年来，稀疏表达理论的兴起为高光谱影像分类提供了新的研究思路和方法.稀疏表达理论认为一个正常信号投影至特定的变换空间能够变为一个稀疏信号，其中的少数非零元素能够很好继承原始信号的特性[5].稀疏表达理论是压缩感知技术的重要理论基础，能够减少数据采集量并采用重构算法来恢复原始信号，目前广泛应用于医疗成像、雷达探测和高光谱遥感成像技术等众多领域[6].高光谱遥感领域中，假设代表同类地物的像元位于统一的子空间，在所有类别训练样本的光谱向量张成的高维空间中，任一像元的空间坐标将表现出明显的稀疏性，仅在同类地物的对应位置上不等于0，其余都应近似或等于0[7].在此基础上，利用重构算法计算每个像元的重构系数向量来确定其属于每一类的重构误差来实现分类.

当前学者利用稀疏表达理论在高光谱影像分类方面已做出一些探索.Chen等提出基于光谱稀疏表达和重构的高光谱影像分类模型[7]，后又提出基于核稀疏表达的改进分类模型来改善分类结果[8].Liu等引入一阶加权邻域系统限制至非负稀疏表达模型中以改善高光谱影像的分类精度[9].近期，国内学者通过光谱维和空间维的联合表达和约束构建每类训练样本的稀疏字典及稀疏表示，并结合最小重构误差和领域相关性约束求解系数向量来实现分类[10].文献[11]提出随机矩阵-非负稀疏表达分类模型，改善传统稀疏表达模型中的等距特性以提高高光谱影像的分类精度[11].当前的稀疏表达模型用于高光谱影像分类主要从单个像元的角度来研究，将一个像元的光谱响应曲线作为单观测向量，利用重构算法来计算其稀疏系数向量进而实现分类.然而高光谱影像作为一个整体数据集，单观测向量(单一像元的光谱向量)的研究视角容易忽略各像元间的相互影响或作用.其次，单观测向量的稀疏表达分类模型遍历单个像元的光谱向量来确定每个像元的类别归属，然而高光谱数据中像元数量巨大，这导致当前稀疏表达分类模型的计算效率较低.

因此，本文引入多观测向量理论，提出基于多观测向量的稀疏表达分类模型(multiple measurement vectors based sparse representation classification, MMV-SRC)，对所有像元同时实现稀疏系数向量求解，利用L2范数约束和稀疏度平衡因子来同时保证各系数向量的稀疏特性，改善现有的单观测向量的稀疏表达分类模型.利用两个高光谱影像数据实验，对比传统的稀疏表达模型，证明本文的分类模型的有效性.

1多观测向量理论

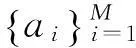
(1)

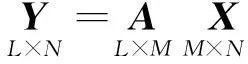
(2)

式中，X=[x1,x2,…,xN]是稀疏系数矩阵，任一信号向量yi=Axi.由于涉及稀疏矩阵X中所有向量xi的求解，常规重构算法无法直接应用到式(2)的病态方程求解中.类似于压缩感知的重构问题，式(2)的求解可以转换为Lp范数优化问题：

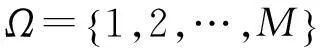
(3a)

s.t. Y=AX

(3b)

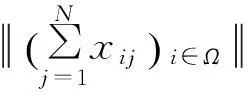
2基于多观测向量的稀疏表达分类

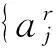
2.1高光谱影像的多观测向量稀疏表达模型

稀疏表达模型假设高光谱影像中同类地物的所有像元都位于统一的高维特征空间.如果任一像元y属于第r类地物，其光谱向量可以看作是位于由第r类地物的训练样本张成的子空间，即y可表达为训练样本矩阵的线性组合[7].进一步，在考虑实际高光谱影像噪声的情况下，如果将像元y在所有类别的训练样本构成的高维空间中展开，则

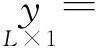
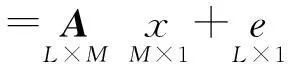
(4)

式中：A为所有类别的训练样本构成的字典矩阵;x=[θ1,θ2,…,θc]T为像元y在训练样本中所有光谱向量所对应的权重系数向量;e为高光谱影像采集过程中存在的随机噪声.当采用多观测向量理论将所有像元的光谱向量排列为一个列矩阵时，式(4)转换为多观测向量的稀疏表达模型，如式(5)所示：

Y=AX+E

(5)

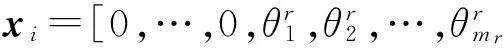
2.2稀疏系数矩阵的求解及高光谱影像分类

式(5)中，由于L≼M，系数向量X并不存在唯一解，其求解过程是一个非凸问题.通常，式(5)中X的非零元素通过求解L0范数的非线性优化问题得到：

(6a)

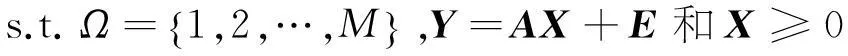
(6b)

考虑到L0范数优化问题的计算复杂度较高，同时考虑到实际优化过程中的逼近误差，本文松弛式(6)中的目标函数至对稀疏矩阵的列向量的L1范数优化问题，

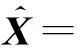
(7a)

s.t. X≥0

(7b)

式中，X(∶,j)为系数矩阵X的第j-列向量，平衡参数β>0用来控制稀疏矩阵X在列方向的稀疏度大小.进一步，式(7)的求解转换为以下非负限制的最小二乘优化问题:

(8a)

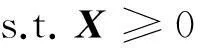
(8b)

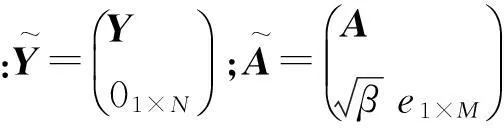
(9)

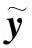
Class(yi)=

(10)

2.3高光谱影像的MMV-SRC分类流程

高光谱影像的MMV-SRC分类的流程如下：

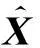
3实验和分析

3.1实验数据

印第安纳数据(下文简称Indian)来自美国普渡大学遥感应用实验室.数据由美国JPL成像光谱仪于1992年6月12日采集得到，空间分辨率为20 m，光谱分辨率为10 nm，光谱区间为200～2 400 nm，预处理后波段数为200.图1为覆盖西拉法叶地区西部8 km的一小块区域，包含145×145像素.图中共包含16类主要地物，其训练和测试样本信息见表1.

城市数据(简称Urban)是美国陆军地理空间中心获取的HYDICE数据.数据采集于1995年10月，空间分辨率为2 m，光谱分辨率为10 nm.影像大小为307×307像素，覆盖美国德克萨斯州科帕拉斯区域(靠近胡德堡)，如图2所示.对原始的210波段数据进行预处理，移除低噪比波段区间[1-4,76,87,101～111,136～153,198～210]，剩余162波段，包含22种主要地物，各地物的训练和测试样本信息见表2.

图1　Indian数据

图2　Urban数据

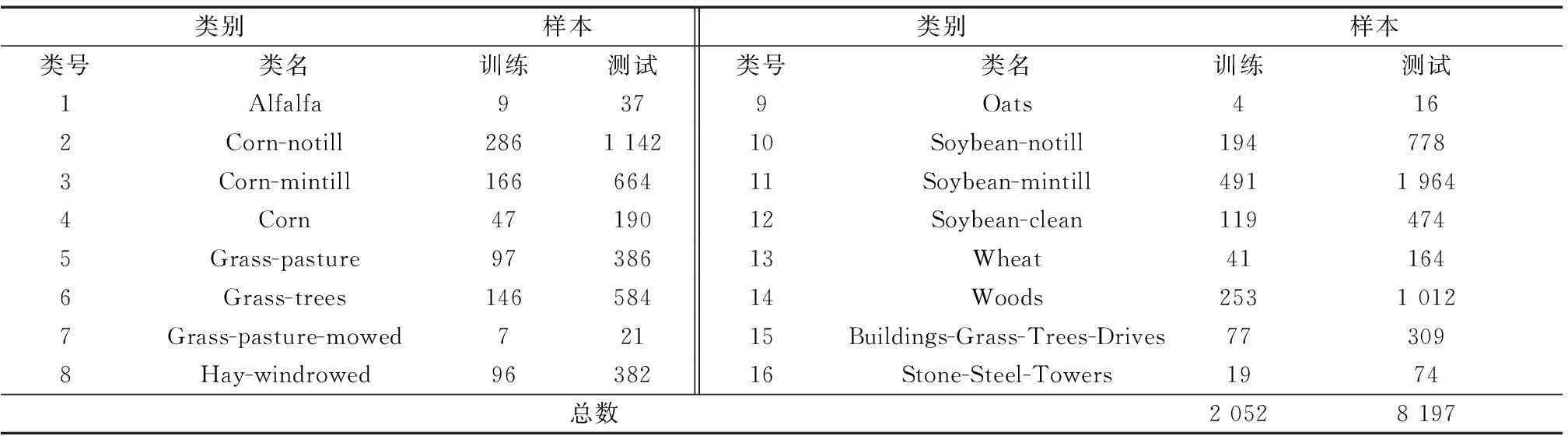
类别样本类别样本类号类名训练测试类号类名训练测试1Alfalfa9379Oats4162Corn-notill286114210Soybean-notill1947783Corn-mintill16666411Soybean-mintill49119644Corn4719012Soybean-clean1194745Grass-pasture9738613Wheat411646Grass-trees14658414Woods25310127Grass-pasture-mowed72115Buildings-Grass-Trees-Drives773098Hay-windrowed9638216Stone-Steel-Towers1974总数20528197

3.2实验分析

本节利用Indian和Urban高光谱影像数据集设计三组实验来验证MMV-SRC方法的性能.实验采用平均分类精度(average classification accuracy, ACA)和总体分类精度(overall classification accuracy, OCA)来定量评价分类结果.首先，对比几种典型的分类器的结果来测试MMV-SRC的分类效果.采用的对比模型有常用的K-近邻(K-nearest neighbors, KNN)分类器、支持向量机(support vector machine, SVM)分类器和基于随机测量矩阵的非负稀疏表达模型(random matrix based nonnegative sparse representation, RM-NSR)[11]和常规的非负稀疏表达模型(nonnegative sparse representation, NSR)[17].其中KNN分类器采用欧氏距离作为相似性度量；SVM分类器中采用径向基核函数，其方差和惩罚因子通过交叉验证获得；RM-NSR模型采用平滑L0范数法[18]来重构稀疏系数向量(简称为RM-NSR(L0))；NSR方法采用正交匹配追踪法(orthogonal matching pursuti, OMP)[19]来重构稀疏系数向量(简称为NSR(OMP)).其次，通过计算实验来对比分析以上5种分类方法的计算效率.最后，研究平衡参数β对MMV-SRC分类器的分类性能的影响.

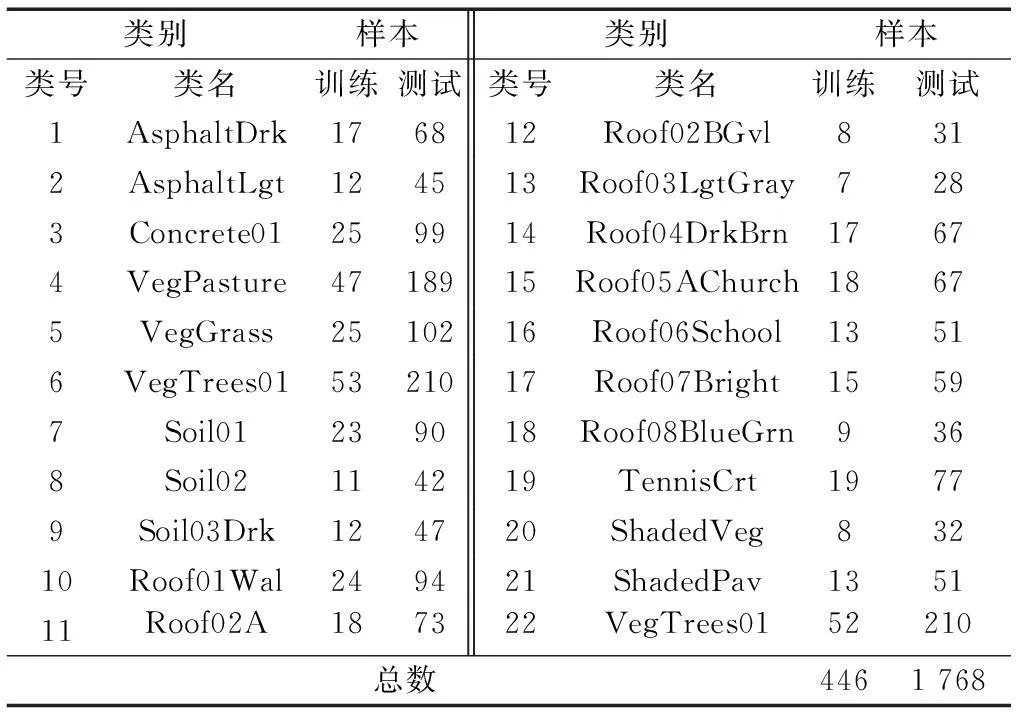
表2　Urban数据的训练和测试样本信息

(1) 分类结果对比

MMV-SRC分类模型和KNN、SVM、RM-NSR(L0)及NSR(OMP)分类模型的结果见表3.表中,括号内数字为标准差.其中MMV-SRC分类器中，迭代次数为5，Indian数据和Urban数据的非零行向量初始值个数分别为400和200.Indian和Urban数据中，KNN分类器中邻域大小k=3.RM-NSR(L0)分类器中，Indian数据的随机矩阵的投影维数P为65，平滑L0范数约束中最小重构误差阈值为0.000 1，迭代次数为100，重构误差下降因子为0.5；Urban数据的随机矩阵的投影维数P为50，平滑L0范数约束中最小重构误差阈值为0.001，迭代次数为80，重构误差下降因子为1.2.NSR(OMP)分类器中，Indian数据的OMP重构方法的阈值设置为0.000 1，迭代次数为10；Urban数据的OMP重构方法的阈值设置为0.000 5，迭代次数为20.

从表3看出，Indian和Urban数据中KNN的分类精度最低，比SVM的ACA和OCA值低幅分别超过10%，这说明SVM的分类性能高于KNN分类器.KNN和SVM分类器的ACA和OCA值低于RM-NSR(L0)和NSR(OMP)，这说明单观测向量的稀疏表达模型的分类性能高于常规KNN和SVM分类器.RM-NSR(L0)的分类精度ACA和OCA分别高于NSR分类器，这同文献[11]中的研究结论保持一致.MMV-SRC的ACA和OCA分类精度高于RM-NSR(L0)和NSR(OMP)，这说明多观测向量的稀疏表达模型的分类结果优于单变量的稀疏表达模型RM-NSR(L0)和NSR(OMP).

表3　Indian和Urban数据中五种分类器的分类结果对比

图3对比Indian数据和Urban数据中5种分类器得到的每一类地物的分类精度.从图3a看出，相比其他分类器，KNN分类器得到的每一类地物的分类精度较低.SVM分类器得到的大多数地物的分类精度低于RM-NSR(L0)和NSR(OMP)，但每一类地物得到的分类精度都高于KNN.RM-NSR(L0)和NSR(OMP)分类器得到的单一地物的分类结果较为接近，不过RM-NSR(L0)的多数地物的分类精度稍高于NSR分类器，这使得RM-NSR的分类精度OCA和ACA都较高.MMV-SRC得到的每一类地物的分类精度都较高，大多数单一地物的分类精度都高于其他4类分类器，尤其在Indian数据中的第4类(Corn，玉米)和Urban数据中第20类(ShadedVeg，遮蔽的植被)和第21类(ShadedPav，遮蔽的道路).因此，以上5种分类器的分类精度结果由高至低排序如下：MMV-SRC、RM-NSR、NSR、SVM、KNN.

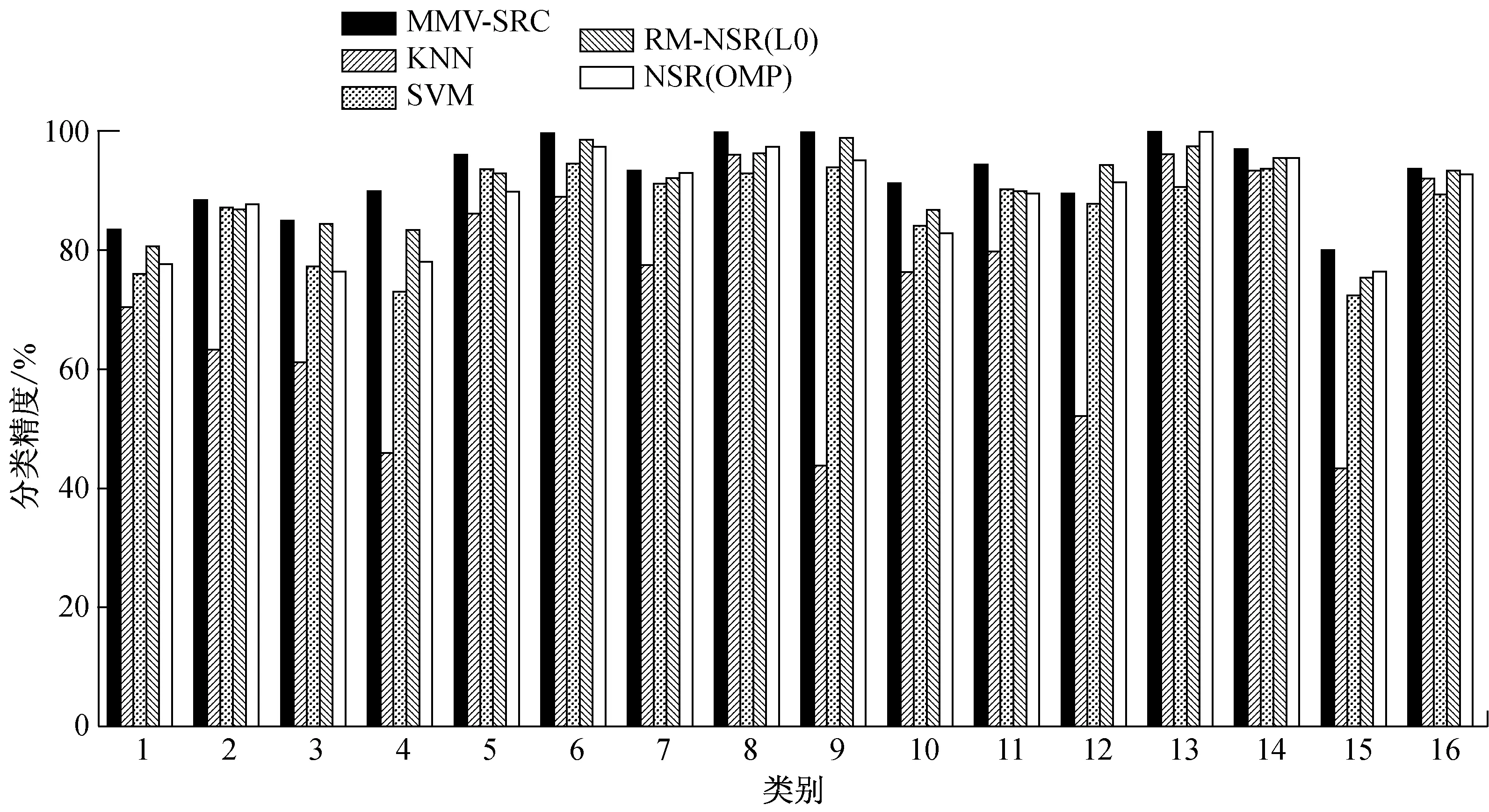
a Indian数据

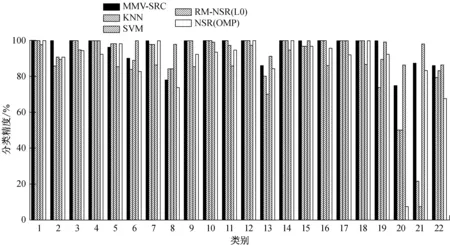
b Urban数据

(2) 计算时间对比

表4列出MMV-SRC和其他4种分类器对Indian和Urban数据集的测试样本进行分类的计算时间.5种分类器的算法都通过MATLAB 2014a编程实现，运算环境为联想i5-4570 四核处理器，8GB内存和Windows 7操作系统.Indian数据和Urban数据的5种分类器的参数设置同实验(1)保持一致.从表4看出，KNN分类器的计算效率最高，所需的计算时间最短.SVM分类所需的计算时高于KNN分类器，但计算速度明显优于RM-NSR(L0)和NSR(OMP)分类器，这是因为RM-NSR(L0)和NSR(OMP)分类器包含大量的非线性优化运算.RM-NSR(L0)分类器的运算效率高于NSR(OMP)，这是由于OMP算法比平滑L0重构方法的计算复杂度高很多.MMV-SRC分类器所需的计算时间高于KNN分类器，但其计算速度优于SVM、RM-NSR(L0)和NSR(OMP)分类器.因此，以上5种分类器的计算速度从高至低排序分别如下：KNN、MMV-SRC、SVM、RM-NSR(L0)、NSR(OMP).

表4　Indian和Urban数据中5种分类器的计算时间对比

(3) 平衡参数β对MMV-SRC分类结果的影响

从式(9)中看出，平衡参数β和最小二乘优化问题的目标解的关系显著，其取值大小能够改变稀疏系数矩阵X的非零元素的结构来影响后续的MMV-SRC分类结果.因此，本实验通过设置不同的平衡参数β取值来探求其与MMV-SRC的分类精度的关系.实验中，Indian数据和Urban数据中平衡参数β的取值区间都为[0.001, 0.005, 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 0.8, 1, 2, 3, 5, 7, 10].Indian数据中，MMV-SRC的非零行向量初始值设置为400，迭代次数为10；Urban数据中，MMV-SRC分类器的非零行向量初始值设置为150，迭代次数为5.

考虑到分类精度ACA和OCA的变化趋势较为相似，图4仅列出平衡参数β和总体分类精度OCA的关系图.从图4a看出，随着β从0.001开始增大，Indian数据中MMV-SRC的OCA逐渐增大.在β=0.2～0.5之间，OCA达到较大值.然而，随着平衡参数β进一步增大，OCA开始呈递减趋势，随着β的增大呈总体递减趋势.图4b中Urban数据的MMV-SRC得到的OCA结果进一步支持上述观察.分类精度OCA随着β从0.001开始增大而得到提高；在β=0.8左右总体分类精度OCA达到较大值；随着β从0.8进一步增大， OCA逐渐呈下降趋势.以上现象的解释是因为β从较小值开始增大，平衡参数β能够调整系数矩阵的非零元素个数，使得每一列的非零系数能够尽量表达其代表的地物的重构信息；然而当β持续增加至过大时，系数矩阵的非零元素过少而导致每一列的系数向量过度稀疏，进而对MMV-SRC的分类结果造成负面影响.因此，根据实验结果，在实际中建议尝试选取介于0.2～0.8之间的β来得到较好的MMV-SRC分类结果.

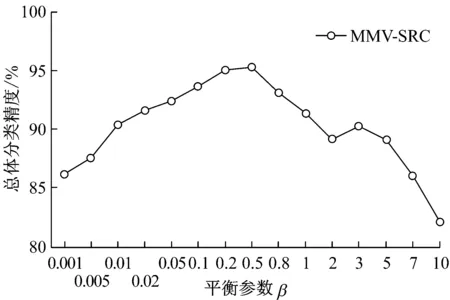
a Indian数据

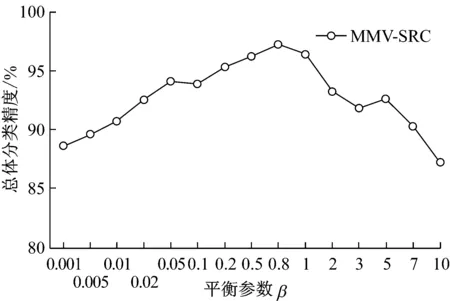
b Urban数据

4结论和展望

考虑到单观测向量的高光谱影像稀疏表达分类模型的不足，本文提出多观测向量的稀疏表达分类(MMV-SRC)模型.MMV-SRC模型将求解测试样本中各像元的类别权重的稀疏系数矩阵的问题转换为基于L2范数约束的逼近误差最小化问题，同时通过引入平衡参数来调节各系数向量的稀疏度；利用稀疏随机卡茨马尔兹算法来得到稀疏系数矩阵，进而根据待测试样本对每一类地物的重构误差大小来确定类别.采用Indian和Urban两个常用的高光谱数据集来验证MMV-SRC的分类性能.实验结果表明，相比KNN、SVM、RM-NSR(L0)和NSR(OMP)分类器，MMV-SRC在具有第二计算速度的同时能够获得最高的分类精度ACA和OCA结果.RM-NSR(L0)和NSR(OMP)的分类结果高于常规的KNN和SVM分类器，然而大量非线性优化运算导致这两种方法的计算效率较低，尤其是NSR(OMP)分类器.另一方面，对MMV-SRC中平衡参数β与分类精度OCA的关系研究发现，过小或过大的β都会影响MMV-SRC在实际中的分类效果.由于β的取值范围和区间较大，本文尚不能做到推荐一个比较合适的平衡参数，只能根据实验结果建议在实际中尝试选择0.2～0.8区间内的值来得到较好的MMV-SRC分类结果.后续的研究将引入参数估计方法来自动或半自动估计得到较好的平衡参数β.此外，本文的MMV-SRC方法涉及到一些其他参数如稀疏随机卡茨马尔兹算法中的迭代次数和非零行向量个数的初始值等，这些目前也只能通过人工估计来选取，这些参数的优化选取和估计也是后续研究需要解决的问题.

致谢作者对王宽诚教育基金会对本文研究工作的资助谨致谢忱.

参考文献:

[1]童庆禧,张斌，郑兰芬.高光谱遥感:原理,技术与应用[M].北京:高等教育出版社, 2006.

TONG Qingxi, ZHANG bing, ZHENG Lanfen. Hyperspectral remote sensing: principle, technology and application[M]. Beijing: Higher Education Press, 2006.

[2]Al-Moustafa T, Armitage R P, Danson F M. Mapping fuel moisture content in upland vegetation using airborne hyperspectral imagery[J]. Remote sensing of Environment, 2012, 127: 74.

[3]Keith D J, Schaeffer B A, Lunetta R S,etal. Remote sensing of selected water-quality indicators with the hyperspectral imager for the coastal ocean (HICO) sensor[J]. International Journal of Remote Sensing, 2014, 35(9): 2927.

[4]Bishop C A, Liu J G, Mason P J. Hyperspectral remote sensing for mineral exploration in Pulang, Yunnan Province, China[J]. International Journal of Remote Sensing, 2011, 32(9): 2409.

[5]Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289.

[6]Divekar A, Ersoy O. Theory and applications of compressive sensing[D]. West Lafayette: Purdue University, 2010.

[7]Chen Y, Nasrabadi N M, Tran T D. Hyperspectral image classification using dictionary-based sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3973.

[8]Chen Y, Nasrabadi N M, Tran T D. Hyperspectral image classification via kernel sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 217.

[9]Liu J, Guan H, Li J,etal. Sparse classification of hyperspectral image based on first-order neighborhood system weighted constraint[C]∥Proceedings of 2005 SPIE Conference in Satellite Data Compression, Communications, and Processing X, Baltimore: SPIE, 2014: 91240Z-91240Z-8.

[10]宋相法,焦李成.基于稀疏表示及光谱信息的高光谱遥感图像分类[J].电子与信息学报, 2012, 34(2): 268.

SONG Xiangfa, JIAO Licheng. Classification of hyperspectral remote sensing image based on sparse representation and spectral information[J]. Journal of Electronics & Information Technology, 2012,34(2):268.

[11]孙伟伟,刘春,施蓓琦,等.基于随机矩阵的高光谱影像非负稀疏表达分类[J].同济大学学报：自然科学版, 2013, 41(8): 160.

SUN Weiwei, LIU Chun, SHI Beiqi,etal. Random matrix-based nonnegative sparse representation for hyperspectral image classification [J]. Journal of Tongji University: Natural Science, 2013, 41(8): 160.

[12]Cotter S F, Rao B D, Engan K,etal. Sparse solutions to linear inverse problems with multiple measurement vectors[J]. IEEE Transactions on Signal Processing, 2005, 53(7): 2477.

[13]Chen J, Huo X. Sparse representations for multiple measurement vectors (MMV) in an over-complete dictionary[C]∥Proceedings of 2005 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP'05), Philadelphia: IEEE, 2005: iv/257-iv/260.

[14]Van Den Berg E, Friedlander M P. Theoretical and empirical results for recovery from multiple measurements[J]. IEEE Transactions on Information Theory, 2010, 56(5): 2516.

[15]Feng J M, Lee C H. Generalized subspace pursuit for signal recovery from multiple-measurement vectors[C]∥2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai: IEEE, 2013: 2874-2878.

[16]Aggarwal H K, Majumdar A. Extension of sparse randomized kaczmarz algorithm for multiple measurement vectors[C]∥The 22nd International Conference on Pattern Recognition(ICPR). Stockholm: [s.n.], 2014: 1014-1019.

[17]Wright J, Yang A Y, Ganesh A,etal. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210.

[18]Mohimani G, Babaie-Zadeh M, Jutten C. Fast sparse representation based on smoothed L0norm[J]. Independent Component Analysis and Signal Separation, 2007(1): 389.

[19]Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655.

Sparse Representation Classification on Hyperspectral Imagery Based-Multiple Measurement Vectors

SUN Weiwei1,2， LIU Chun3,4， LI Weiyue5,6

(1. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, Hubei, China； 2. College of Architectural Engineering, Civil Engineering and Environment, Ningbo University, Ningbo 315211, Zhejiang, China； 3. College of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China； 4. Key Laboratory of Advanced Engineering Survey of NASMG(National Administration of Surveying, Mapping and Geoinformation of China), Shanghai 200092, China； 5. Institute of Urban Studies, Shanghai Normal University, Shanghai 200234, China； 6. Key Laboratory of Mining Spatial Information Technology of NASMG, Jiaozuo 454000, China)

Abstract：Traditional sparse representation based classifiers ignore inter-connections among pixels and have high computational complexity when applied in hyperspectral imagery (HSI) field. Therefore, a multiple measurement vectors based sparse representation classifier (MMV-SRC) model is proposed to solve the above problems. The model introduces a balance parameter to control the sparsity of coefficient vectors, and estimates sparse coefficient vectors of all testing pixels by minimizing reconstruction errors using the L2-norm constraint. Experiments on two HSI datasets are implemented to test the performance of MMV-SRC, and the results are compared with those of five state-of-the-art classifiers. The results show that MMV-SRC achieves best classification accuracies among all whereas taking the second shortest computational time.

Key words：multiple measurement vectors; sparse representation; hyperspectral imagery; classification

文献标志码：A

中图分类号：P237

基金项目：国家自然科学基金(41401389,41371333)；对地观测技术国家测绘地理信息局重点实验室开放课题(K201505)；宁波市社发领域科技攻关项目(2014C50067)；宁波市自然科学基金(2014A610173)；宁波大学科研基金(XYL15001)；浙江省教育厅科研项目(Y201430436)；宁波大学学科建设项目(ZX2014000400)；上海师范大学一般科研项目(SK201525)；矿山空间信息技术国家测绘地理信息局重点实验室开放基金(KLM201309)

收稿日期：2015-03-30

第一作者： 孙伟伟(1985—)，男，工学博士，副教授.主要研究方向为高光谱遥感处理理论和方法及“3S”理论在城乡规划和海岸带资源环境管理中的应用研究.E-mail:nbsww@outlook.com