基于一机双天线站间单差的周跳探测与修复

王明华， 王解先， 董大南， 陈　雯

(1. 同济大学 测绘与地理信息学院，上海 200092； 2. 国土资源部地学空间信息技术重点实验室，成都 610059；

3. 空间信息和定位导航上海高校工程中心，上海 200241)



基于一机双天线站间单差的周跳探测与修复

王明华1,2， 王解先1， 董大南3， 陈雯3

(1. 同济大学 测绘与地理信息学院，上海 200092； 2. 国土资源部地学空间信息技术重点实验室，成都 610059；

3. 空间信息和定位导航上海高校工程中心，上海 200241)

摘要：基于对短基线单差模型的分析，使用站间载波相位观测值之差的变化率作为周跳检测量，对该量进行数值估算，分析钟跳对该量的影响，从理论上证明该检测量可用于一机双天线单差短基线解算中的周跳探测，并提出相应的周跳探测与修复方法.采用实测数据进行实验分析，结果表明，对于一机双天线短基线数据，该方法不受钟跳影响，能有效探测和修复周跳.

关键词：时钟同步； 一机双天线； 单差模型； 周跳探测； 钟跳

根据各天线是否同步接收数据，一机多天线接收机可以大致分为两种类型.第一种类型的基本思路[1]是不改变全球定位系统(global positioning system,GPS)接收机的结构，通过一个GPS多天线切换开关来连接多个天线，接收机在某一个时刻只接收一个天线的数据.这种一机多天线接收机已经在大坝、桥梁、滑坡等的监测中得到应用[2].第二种一机多天线接收机能同步接收多个天线的数据，这种接收机是一种较为新型的产品，目前应用较多的是双天线接收机，国际上Trimble[3]和Javad[4]等公司在21世纪后推出该类产品，国内司南导航[5]近两年开发出此类产品.由于共用一个接收机时钟，各天线数据保持严格同步，因此两天线间(站间)观测数据求差在消除卫星钟差的同时还能消除接收机钟差，可实现传统双差的效果.双差模型要在星间和站间各求一次差，而采用站间单差模型只在站间求一次差，因此解算时观测方程更多而且观测噪声更小.然而，由于单差模糊度固定等方面问题尚未彻底解决，目前还主要用双差算法以及双差模型所对应的模糊度固定与周跳探测方法等，接收机时钟同步的优势尚未得到充分利用.为发挥该接收机硬件优势，开发基于该类产品的单差算法具有重要意义，而对应的周跳探测方法研究是一项重要的前期工作.

准确的周跳探测是利用载波相位实现高精度定位的前提.目前，已有很多周跳探测方法，概括起来，大致可以分为三大类[6]：基于观测值变化规律的探测方法，如多项式拟合法、高次差法；基于多类观测值组合的探测方法，如M-W组合法，电离层残差法[7-8]；基于观测值估值残差的探测方法,如三差观测值残差法.根据在一些基本观测量上使用的预测、滤波方法的不同，周跳探测方法还可以划分为：基于时间序列的探测方法[9]；基于卡尔曼滤波的探测方法[10]；基于小波变换的方法[11-12];基于灰色预测理论的方法[13]等.尽管各种方法有各自的独特性，但周跳探测的基本思想是一致的，即先构造出一检测量，这一检测量在正常情况下(无周跳)是平滑的，而当周跳出现时，将破坏这种平滑性，因此能够根据平滑性发生破坏的历元和破坏程度推断出周跳发生的位置以及周跳大小.

基于以上分析，研究适用于时钟同步一机双天线的周跳探测方法，关键在于寻找或者构建一平滑性好、对周跳敏感的检测量.通过站间观测值差分来构造周跳检测量，这一检测量虽然能消除与卫星相关的误差，但对于传统类型接收机而言，由于两测站接收机钟差之差对检测量的影响较大(即使两接收机钟的稳定度均达到10-9s·s-1，在1 s时间间隔，由两钟差之差造成的影响最大可达0.6 m左右，对应于L1载波的3周)，检测量平滑性差，无法用于探测、修复小周跳[14].然而，时钟同步一机双天线由于两天线共用时钟，站间差分后理论上不存在接收机钟差的影响，站间差分构造的检测量平滑性大大改善，因此本文拟通过一机双天线观测值站间差分，并以差分值的变化率作为周跳检测量，分析与估算其范围，并证明该检测量用于周跳探测与修复的有效性.

1周跳检测量

1.1单差模型与检测量

GPS载波相位观测方程如下所示：

(1)

式中：i表示测站编号或天线编号(i取1、2)；s表示卫星编号；t表示观测历元；φ为载波相位观测值；ρ为站星几何距离；c为光速值；VRi为接收机钟差；VTs为卫星钟差；N为模糊度；λ为波长值；Vion为电离层延迟量；Vtrop为对流层延迟量；ε为观测噪声以及多路径误差等难以模型化的误差.ε在实际计算时并不知道具体数值，通常是采取一定措施将其限制在一定范围内.

对同一颗观测卫星，在同一观测历元，将两测站载波相位观测值进行求差，即站间单差，得到如下：

(2)

其中，f代表载波频率;各符号下标1,2分别表示天线1与天线2所对应的观测量;Δε(t)=ε1-ε2.

对于时钟同步一机双天线接收机，两天线共用时钟，式(2)右端第二项为0，并且双天线接收机一般应用于短基线(数米至数十米)，两天线相应的电离层与对流层延迟认为高度相关，求差后可基本消除，所以可对式(2)作进一步简化，得如下单差观测方程：

(3)

从式(3)可以看出，对于时钟同步一机双天线接收机，其站间单差就已经消除了卫星钟差和接收机钟差，单差模型可替换传统的双差模型.

1.2检测量数值范围估算

由第1.1节可知，Δφs(t)变化率能作为周跳探测检测量的前提是正常情况下其数值较小，并且在一定范围内，因此，本节先对Δφs(t)在无周跳时的变化率进行估算，给出Δφs(t)变化率的范围估值，再证实Δφs(t)的变化率能作为周跳检测量以及初步分析其周跳探测与修复能力.

(4)

其中t1、t2为相邻两历元时刻.

将式(4)两端取绝对值，并将式(3)代入式(4)得：

(5)

式(5)中ΔΔε=Δε(t2)-Δε(t1)，Δρs(t)为两天线站星距之差，表达式如下：

(6)

Δρs(t)随时间变化的示意图如图1所示.图中，α为两天线的卫星视方向夹角，β为卫星的运动速度方向与卫星至其中一个天线方向之间的夹角.v(t)为卫星运行速度.

图1　站星距差Δρs(t)变化示意图

(7)

式(7)右端第一项(站星距离差变化率)还可以作如下变换：

(8)

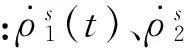
(9)

根据图1所示的几何关系，可得如下关系式：

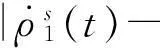
v(t)|cosβ-cos(α+β)|

(10)

因此

(11)

式(11)中v(t)max为卫星最大运行速度，α可根据基线长度及天线至卫星的距离计算出，β根据使|cosβ-cos(α+β)|取得最大值而确定.

估计式(9)右端第一项上界时，从数值最大化方面考虑，本文取卫星最大运行速度为3 500 m·s-1，天线至卫星的距离取20 000 km(为使α值尽量大)，β取π/2-α/2(此时|cosβ-cos(α+β)|取得最大值)，估计的结果如表1所示：

表1　站星距离差变化率上限估值

表1说明，当基线长度不超过15 m时，站星距离差变化率(式(7)右端第一项)不超过0.0137 周·s-1(相应于L1载波)或0.0107 周·s-1(相应于L2载波).当基线长度不超过100 m时，站星距离差变化率不超过0.1 周·s-1.

1.3接收机钟跳对检测量的影响

随着数据采集过程的进行，GPS接收机内部时钟会逐渐漂移，为了使其与GPS时间同步，一般会采取钟跳措施[7，15-16].钟跳会影响测码伪距以及载波相位观测值，对某些周跳探测方法会产生一定的影响.当接收机钟稳定性差，观测过程中可能发生多次钟跳，此时在周跳探测中有效的处理钟跳显得较为重要.

假设某一观测时刻T=t+δt，若发生钟跳，且钟跳值为δt，则将T时刻对应的载波相位观测值记为φs(T)，若未发生钟跳，则将T时刻对应的载波相位观测值记为φ*s(T)，则两者的关系为[15]

(12)

而钟跳对相位观测值差分值的影响如下：

(13)

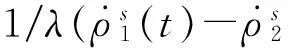
2周跳探测与修复方法

2.1检测量突变类型

图2和图3中,横轴为历元编号，纵轴为周跳检测量的数值.两图中周跳或粗差均发生在第8 051历元.

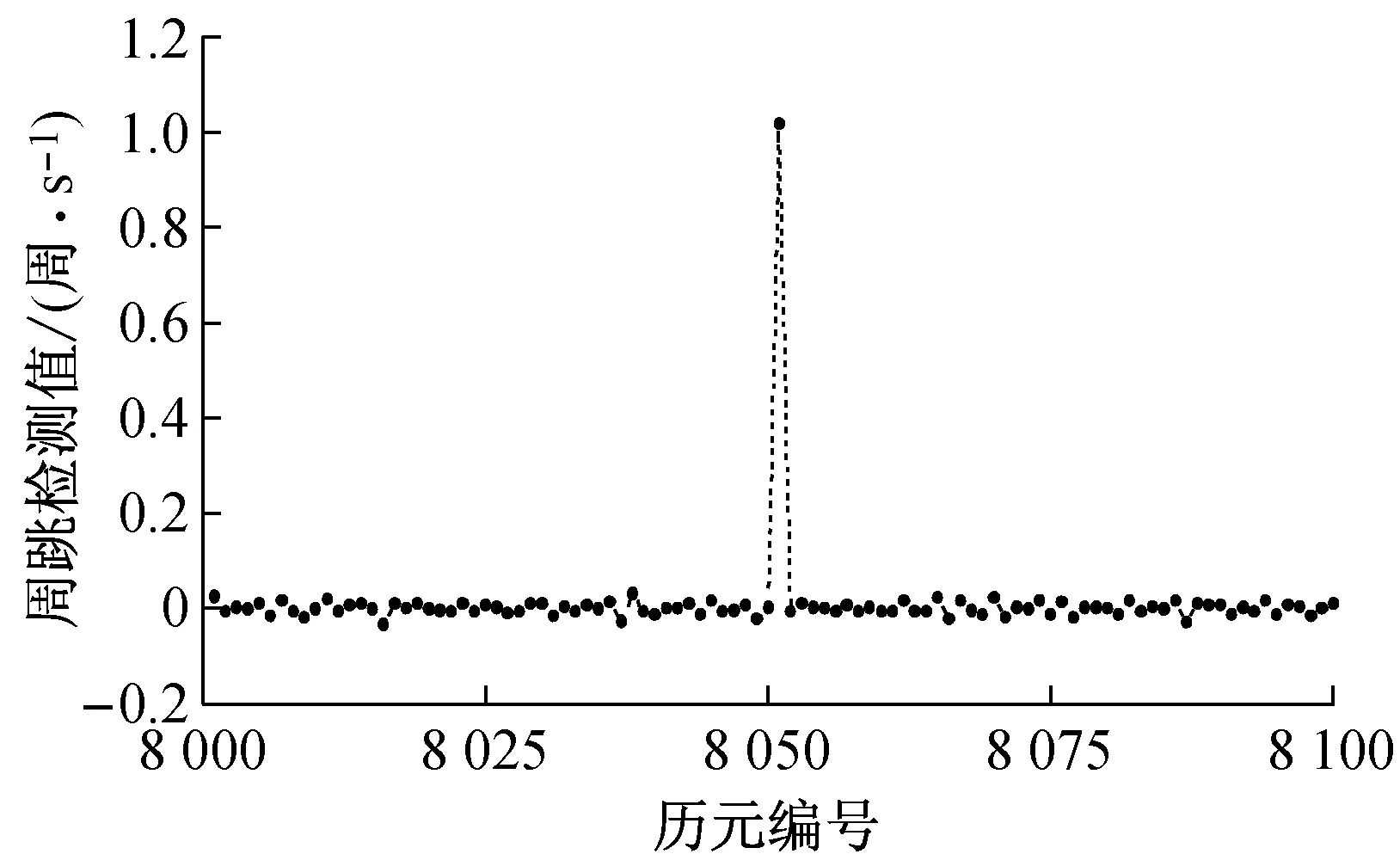
图2　周跳示意图

图3　粗差示意图

2.2周跳探测方法及修复分析

在第2.1节分析检测量突变类型的基础上，确定本文的周跳探测方法，具体步骤为：

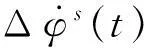
(2)对每颗卫星，从第二历元起计算每一历元周跳检测量的数值T(由式(4)知，第一个历元无法计算检测量)；

(3)判断每一历元检测量的值是否满足T∈(-R,R)条件，若满足条件，则认为正常，若不满足，则认为当前历元检测量发生了突变，继续判断下一历元是否满足T∈(-R,R)条件，若下一历元满足条件，则认为当前历元发生周跳，若下一历元不满足条件，则认为当前历元数据含粗差.

(14)

可探测最小周跳数为满足式(14)n(n为正整数)的最小取值.

本文中，若根据式(14)确定的可探测最小周跳为1周，则可以进行周跳修复，若可探测最小周跳大于1周，则无法准确修复周跳.满足周跳修复条件时(即1/Δt>2R成立时)，当在某历元发生周跳，检测量T∉(-R,R)，此时可取一整数m，使T∈(m/Δt-R,m/Δt+R)，则m即为应修复的周跳数值，m的计算公式如下：

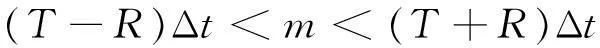
(15)

满足周跳修复条件时，式(15)中m的整数解唯一.

3实验分析

本文实验数据采用天宝BD982时钟同步一机双天线接收机采集，数据采集地点为某教学楼楼顶，两天线相距约12 m，数据采集时间为2014年积日250和251两天，数据采样间隔为1 s.

3.1钟跳影响

第1.3节从估算的角度说明了钟跳对本文周跳检测量的影响较小，可以忽略不计，以下将根据具体实验数据来验证这一结论.对年积日第250 d的数据，选取其中一个天线进行伪距单点定位，计算出接收机钟差值，确定钟跳发生的历元，任意选取其中两个钟跳历元，并计算出两颗卫星在钟跳历元及其前后若干历元对应的检测量数值，结果如图4所示.

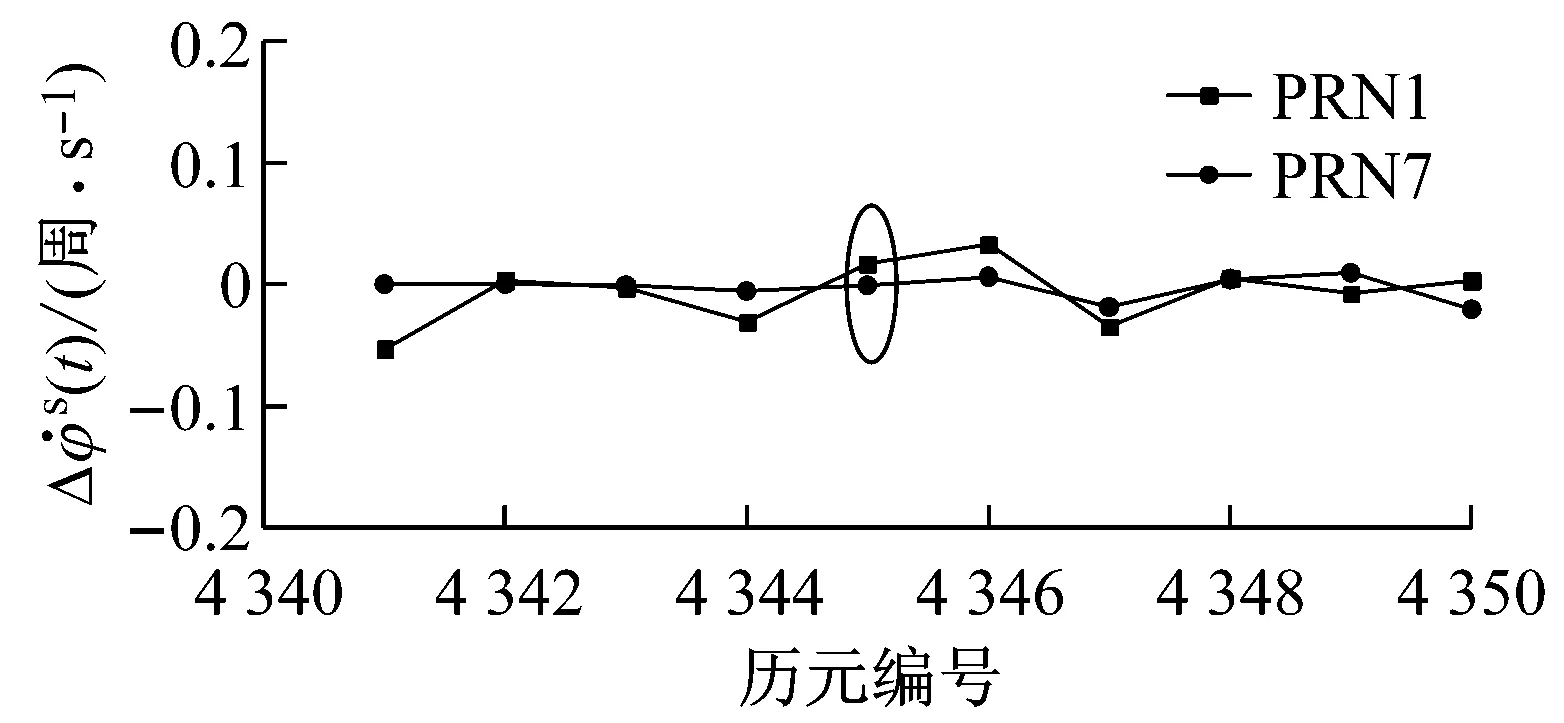
a

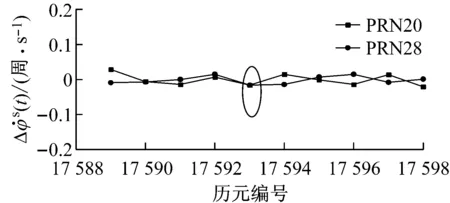
b

图4a中第4 345历元与图4b中第17 593历元均为钟跳发生历元(图中黑色圈所标)，从以上两图看，钟跳的发生并未对1、7、20以及28号卫星对应的周跳检测量造成显著影响，这验证了1.3节的推导结论.

3.2检测量数值统计

以年积日为第250 d的实际观测数据(取L1载波数据)为研究对象，统计无周跳历元检测量的数值上界，结果如图5所示(采样间隔1 s)：

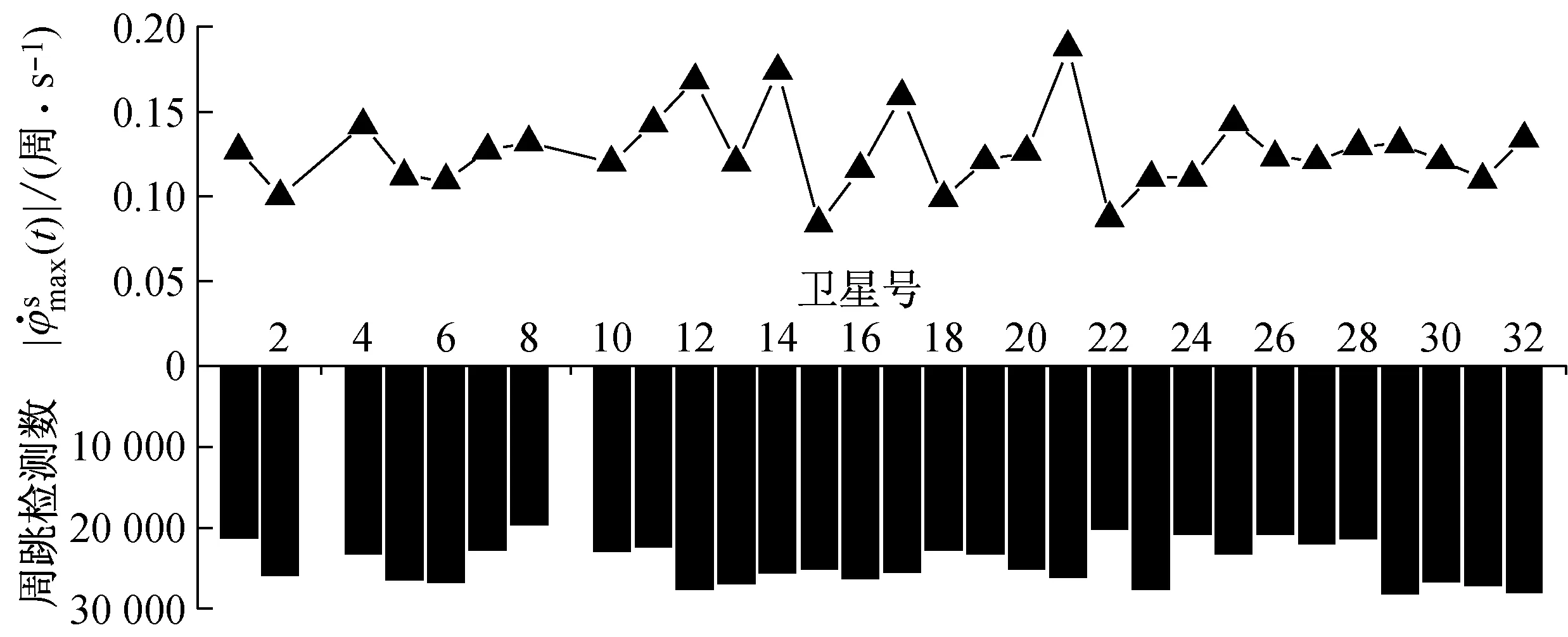
图5　各卫星观测数据最大周跳检测量统计

(1)估计得出的范围是正确有效的；

(2)估计的范围略大于统计的范围，这是因为估计时式(9)右端第一项的估值被放大，并且由于无法准确确定右端第二项|ΔΔε|限值，而将该限值取一个较大的值(例如文中取5cm，实际中可能小于这一数值)，从而导致估计范围偏大.若事先具备一定的先验信息，可确定|ΔΔε|更为准确的限值，则估计的范围也将更加准确.

3.3周跳探测与修复结果

采用年积日第251d的数据(取L1载波数据)，在无周跳的数据中加入一定的周跳和粗差，以此检验本文方法的周跳与粗差探测及修复效果.为检验本文方法对低采样率数据周跳探测与修复效果，将年积日第251d的原始1s采样间隔数据进行重采样，获得15s采样间隔的数据，并进行周跳探测与修复实验.

根据第1.2节的估算方法，估计检验量的正常范围(估计时基线长取12m，|ΔΔε|限值取5cm)，对于采样间隔为1s的数据，其检测量正常范围估值为(-0.273 7,0.273 7),周·s-1，对于采样间隔15s数据，其检测量正常范围估值为(-0.028 5,0.028 5),周·s-1.由式(14)可知，两种采样间隔下的数据均满足周跳修复条件.根据估计的检测量正常范围，进行周跳探测与修复，结果如表2所示.

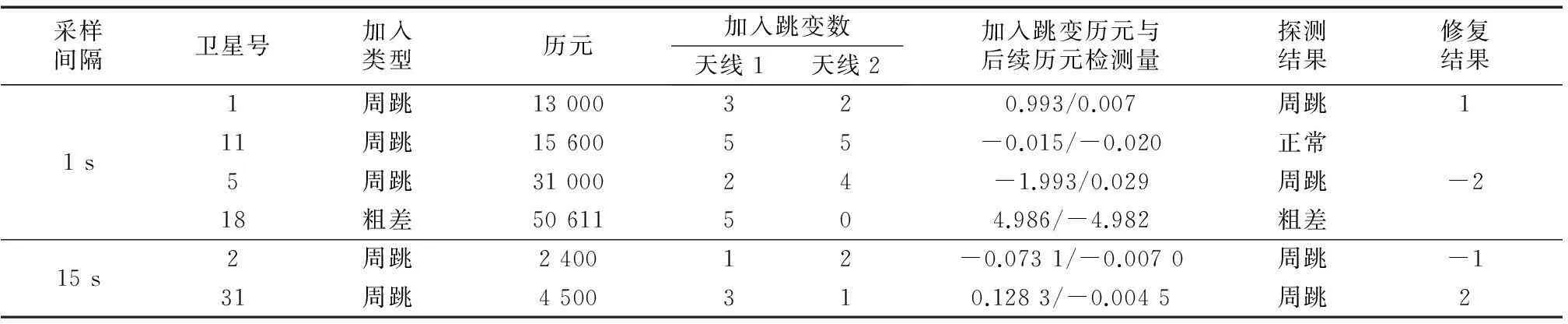
表2　周跳探测及修复实验结果

表2中第4列“历元”表示从该历元起加入跳变，例如13 000表示从第13 000历元起加入跳变.第7列“加入跳变历元与后续历元检测量”为加入跳变的历元以及其后续一个历元的检测量的值(周·s-1)，根据这两个值可以判断是否发生周跳或粗差.第8列“探测结果”为本文方法判断的跳变类型.第9列“修复结果”为根据本文周跳修复方法确定的周跳值.

对于1 s采样间隔数据，1号卫星从13 000历元起天线1加入3周跳变，天线2加入2周跳变，根据式(3)知，其对Δφs(t)的理论影响值为1周.1号卫星检测量值如图6所示.

图6　1号卫星检测量

从1号卫星对应的第7列数据“0.993/0.007”，可知在第13 000历元检测量发生突变(0.993∉(-0.273 7,0.273 7))，而第13 001历元正常(0.007∈(-0.273 7,0.273 7))，判断在第13 000历元发生周跳.且根据式(15)(此时T=0.993,R=0.273 7,Δt=1)可计算出应修复的周跳值m为区间(0.719 3,1.266 7)中的整数，因此求得m为1，与理论值相同.5号卫星与1号卫星情况相似.11号卫星，由于从第15 600历元起对两天线加入相同的周跳值，其对Δφs(t)并无影响，因此不判断为周跳.18号卫星第7列“4.986/-4.982”，即第50 611历元4.986∉(-0.273 7,0.273 7)，第50 612历元-4.982∉(-0.273 7,0.273 7)，因此判断第50 611历元数据中有粗差，这一判断结果也与理论值一致.

对于15 s采样间隔数据，其检测量的正常范围为(-0.028 5,0.028 5)，周跳修复时R值取0.028 5，Δt值取15，对2号与31号卫星的探测与修复结果均正确.

4结语

本文基于时钟同步一机双天线数据构建的周跳探测检测量平滑性好，有效避免了钟跳的干扰，周跳的修复与后续单差模糊度固定相对应.经实测数据验证，周跳探测与修复的效果较好，能有效探测和修复1周周跳，该方法原理简单，易于程序实现.虽然，随着基线增长以及采样间隔增大，本文方法的周跳探测与修复能力会有所下降.然而，当前时钟同步一机双天线接收机主要用于短基线应用，而且接收机均能接收高频数据(采样间隔小)，因此本文方法在时钟同步一机双天线接收机应用领域可普遍适用.

参考文献:

[1]Ding X L, Chen Y Q, Huang D F,etal. Slope monitoring using GPS: a multi-antenna approach [J]. GPS World, 2000(3): 52.

[2]何秀凤，华锡生，丁晓利,等. GPS一机多天线变形监测系统[J].水电自动化与大坝监测，2002，26(3):34.

HE Xiufeng, HUA Xisheng, DING Xiaoli,etal. Development of GPS multi-antenna based deformation monitoring system [J]. Hydropower Automation and Dam Monitoring, 2002, 26(3):34.

[3]Trimble Co. Ltd. Trimble's BD982 dual-antenna receiver designed for specialized apps [J]. GPS World, 2010, 21(4): 25.

[4]Javad GNSS, Inc. Satellite differential positioning receiver using multiple base-rover antennas [P]. US: 2012/0139784 A1, 2012-02-08.

[5]ComNav Technology Ltd. ComNav OEM board reference manual[EB/OL]. [2014-01-15]. http://www.comnav.cn.

[6]李征航，张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉：武汉大学出版社，2009.

LI Zhenghang, ZHANG Xiaohong. New techniques and precise data processing methods of satellite navigation and positioning[M]. Wuhan: Wuhan University Press, 2009.

[7]Blewitt G. An automatic editing algorithm for GPS data[J]. Geophysical Research Letters, 1990, 17(3):199.

[8]王维，王解先，高俊强. GPS周跳探测的方法研究 [J]. 武汉大学学报：信息科学版，2010, 35(6):687.

WANG Wei, WANG Jiexian, GAO Junqiang. Cycle slip detection of GPS data[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6):687.

[9]滕云龙，师奕兵，郑植. 时间序列分析在周跳探测与修复中的应用 [J]. 宇航学报，2011, 32(3):543.

TENG Yunlong, SHI Yibing, ZHENG Zhi. Time series analysis and its application in detection and correction of cycle slip[J]. Journal of Astronautics, 2011, 32(3):543.

[10]刘伟平，郝金明，汪平，等. Kalman滤波在周跳探测与修复中的应用 [J]. 大地测量与地球动力学，2009, 29(6):101.

LIU Weiping, HAO Jinming, WANG Ping,etal. Study on cycle slip detection and repair by use of kalman filtering [J]. Journal of Geodesy and Geodynamics, 2009, 29(6):101.

[11]蔡昌盛，高井祥. GPS周跳探测及修复的小波变换法 [J]. 武汉大学学报：信息科学版，2007, 32(1):39.

CAI changsheng, GAO jinxiang. Cycle-slip detection and correction of GPS data by wavelet transform[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1):39.

[12]黄丁发，卓健成. GPS相位观测值周跳检测的小波分析法 [J]. 测绘学报，1997, 26(4):352.

HUANG dingfa, Zhuo jiancheng. Wavelet analysis for cycle slip detection and reconstruction of GPS carrier phase measurements [J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(4):352.

[13]王成，王解先. 单频非差相位观测值的周跳探测与修复方法 [J]. 同济大学学报：自然科学版，2012,40(9):1393.

WANG cheng, WANG Jiexian. Cycle slip detection and correction of single frequency un-differenced phase observation[J]. Journal of Tongji University: Natural Science, 2012, 40(9):1393.

[14]李征航，黄劲松. GPS测量与数据处理 [M]. 2版. 武汉：武汉大学出版社，2010.

LI zhenghang, Huang jingsong. GPS Surveying and Data Processing [M]. 2nd ed. Wuhan: Wuhan University Press, 2010.

[15]Kim D, Langley R B. Instantaneous real time cycle-slip correction for quality control of GPS carrier-phase measurements [J]. Navigation, 2002, 49(4): 205.

[16]张成军，贾学东. 接收机钟跳对GPS定位的影响及探测方法 [J]. 测绘通报，2009(12):7.

ZHANG Chengjun, JIA Xuedong. The influence and detection method of receiver clock jumps on GPS positioning [J]. Bulletin of Surveying and Mapping, 2009(12):7.

Detecting and Repairing Cycle-slip for Clock-Synchronized Dual-antenna Global Positioning System Data based on Single-differencing between Antennas

WANG Minghua1,2, WANG Jiexian1, DONG Danan3, CHEN Wen3

(1．College of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China；2. Key Laboratory of Geo-special Information Technology of the Ministry of Land and Resources, Chengdu 610059, China；3. Engineering Center of Shanghai Municipal Education Commission for Space Information and Global Navigation Satellite System, Shanghai 200241, China)

Abstract：Based on the algorithm of single-differencing for short baseline, this paper adopts the rate of phase-differencing between two antennas as the indicator of cycle-slip detection. We estimated the normal range of the rate and examined the effect of clock jump on it. Our theoretical analysis demonstrates that this indicator is able to detect cycle-slip effectively. A numerical method for detecting and correcting cycle-slip is provided. The experiments with real short baseline data from the clock-synchronized dual-antenna receiver show that this method is valid in detecting and repairing the cycle slips, and it is immune to the disturbance of clock jumps.

Key words：clock synchronization; dual-antenna receiver; single-differencing algorithm; cycle-slip detection; clock jump

文献标志码：A

中图分类号：P228

通讯作者：董大南(1947—)，男，国家“千人计划”入选者，教授，博士生导师，主要研究方向为空间大地测量与地球物理.

基金项目：上海市科委科技创新行动计划重大项目(13511500300)；国家自然科学基金(41174023；61372086)；国土资源部地学空间信息技术重点实验室开放基金项目(KLGSIT2013-13)

收稿日期：2015-05-17

第一作者： 王明华(1983—)，男，博士生，主要研究方向为GNSS数据处理.E-mail：wmhua@126.com

E-mail：dndong@cs.ecnu.edu.cn