上证指数波动性的实证研究———基于EGARCH模型

孙林科

（福建师范大学，福建 福州 350108）

上证指数波动性的实证研究
———基于EGARCH模型

孙林科

（福建师范大学，福建 福州 350108）

衡量一个国家股票市场风险指标的关键在于股指的波动性，这对股市甚至整个宏观经济有着重要的影响。本文以上证指数2004年01月02日～2016年2月29日的日收益率的波动情况为数据样本，利用EGARCH模型进行实证分析。

上证指数；波动率；EGARCH模型；杠杆效应

一、引言

证券市场的波动是投资者、企业和监管部门，甚至每一个中小股民都深切关注的话题，同时学者们也希望能更好地刻画股指乃至个股票价格的波动，以使投资者能更加清晰地认识到自己面临的风险和应获得的风险溢价，从而提高整个证券市场的效率。

目前，我国证券市场依然处于成长期，股票指数的波动性也高于发达国家成熟市场。2008年金融危机导致全球股市暴跌，为了刺激经济复苏，发达国家纷纷采取措施挽救经济，股市也呈现出修复性上涨。但中国股市却背道而驰，在金融危机之前就出现连续暴跌，在其他国家股市上涨的时候，在2012年出现了四年来的新低，成为全球股市表现最差之一。因此，研究上证指数波动，如何更好地衡量股指波动对股票投资人和中国经济的影响十分重要。

二、文献综述

国外证券市场的发展相对成熟，经历了更多的股市大波动，对于股票市场的波动性，聚类性和持续性是其最显著的特征。诸多实证结果表明GARCH模型已经能反映大多数金融产品价格的波动性，之后GARCH又被推广为EGARCH模型、TGARCH模型和PGARCH模型等组成GARCH族。

国内的学者对此类模型研究较晚，在汇率、股指期货方面有所突破。骆殉、吴建红（2009）运用2003--2007年之间的1069个美元兑人民币汇率日值，应用GARCH模型进行分析，证实了我国外汇市场确实存在ARCH效应，且GARCH模型能够较好地拟合汇改后的人民币汇率数据；林德钦（2014）运用对创业板指数波动率进行实证分析时通过大量的实验证明发现AR（1）-GARCH（1，1）模型对创业板指数波动率的预测更为有效；魏正元，张鑫，赵瑜（2015）采用高频金融数据进行分析发现偏t分布的R-GARCH（1，2）模型更适合上证380的实证分析，同时精确衡量的收益风险。

在研究上证指数时主要运用EGARCH模型，通过对模型的数据样本做效应分析和检验，确定上证指数收益率使用哪种模型，然后设计合理科学的模型，再使用模型进行实证分析，给出结论和投资的股市政策建议。

三、模型简介

GARCH模型的定义为：

其中，ht是εt的条件异方差，在模型中为了保证ht为正就必须使得琢i，茁i为正。因为条件方差方程中待估参数均取非负值，其约束条件很强，会限制条件方差时刻变化的特性，所以我们选择更为有效的EGARCH模型。

EGARCH模型的定义为：

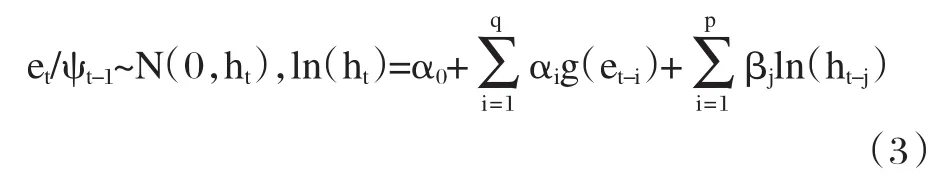
整理之后的EGARCH（p，q）模型常用的方差表达式为：

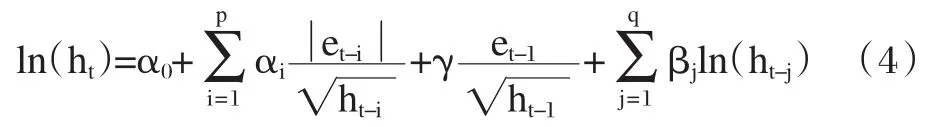
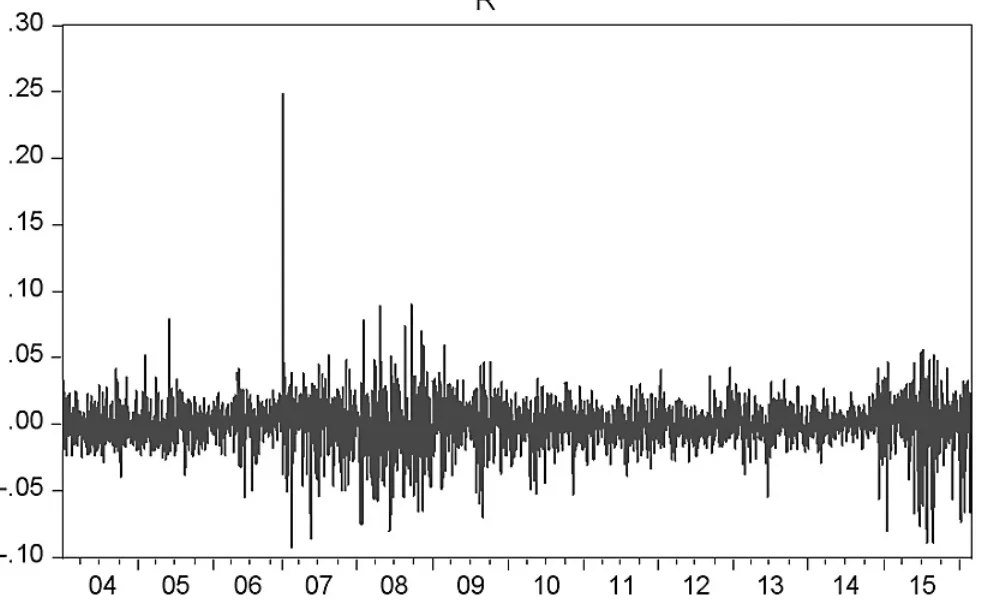
图1 上证指数日收益直线图

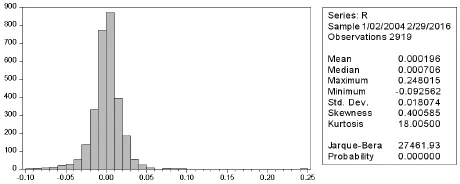
图2 上证指数日收益直方图

图3 自相关系数以及偏自相关系数

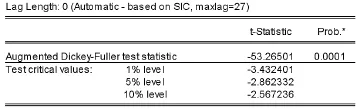
图4 ADF检验的结果

四、实证分析

1、数据处理以及特征

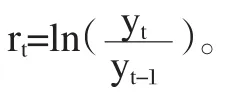
从图1和图2可以看出波动的聚集现象，波动在一段时间内很小，在其他的一段时间里非常大，说明误差项可能具有条件异方差性。在所选样本序列中包含的2920个数值的均值为0.000196小于中位数，说明右偏。偏度s=0. 400585，K=18.005，说明收益率分布具有尖峰的特征，同时收益分布图的左右两端出现观测值，说明具有拖尾特征。

2、ARCH效应分析和检验

滞后一阶和滞后二阶的值都较大，认为不具有自相关性。从滞后三项开始，值明显减小，认为三阶以上存在自相关性。

（1）平稳性检验。为了确定rt的平稳性，对其进行平稳定性检验，结果如图4。在1%的显著水平下，收益率rt的ADF统计量为-53.26501远远小于临界值-3.4318，p值几乎为0，说明rt有一个单位根的概率几乎为0，可以认为具稳定性。

（2）异方差性检验。从图1、图2中可以看出，rt的样本分布具有聚类特征，从统计的角度来说，rt序列具有异方差性。下面用ARCH检验来检验序列的异方差性，结果如下：

F统计量为14.55079，P值几乎为0，说明模型显著，观察值R2为14.48845，P值几乎为0，说明拒绝ARCH模型残差项不存在异方差性的原假设，即所选上证综合指数收益率样本存在明显的异方差性。综合上述对上证指数收益率样本序列的ARCH效应（平稳性、自相关性、异方差性）的分析检验，有理由认为使用GARCH模型来描述收益率的波动性是合理的。

3、模型构造

我们发现GARCH模型的另一个缺陷是要求估计参数为正，但一般来讲估计出来的参数不符合这个过于苛刻的限定。在EGARCH模型中，在表达式中并不要求估计参数一定要为正，EGARCH模型的参数可以由最大似然估计给出。假定Zt服从广义误差分布，密度函数为：

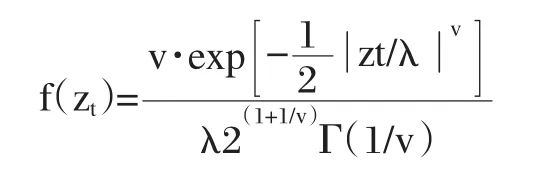
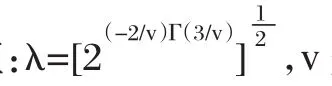
EGARCH模型在实际应用中常用EGARCH（1，1）的条件方差表达式为：

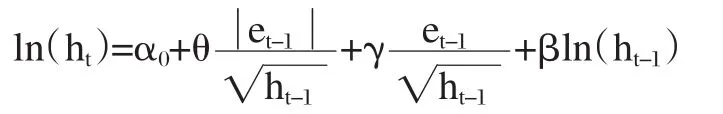
4、模型的确定以及结果分析

在ARMA（2，1）基础上建立EGARCH模型，我们分别使用了EGARCH（1，0）、EGARCH（0，1）、EGARCH（1，1）、EGARCH（2，1），经过多次拟合比较实验数据发现使用EGARCH（1，1）模型估计较为合适，估计的结果为：

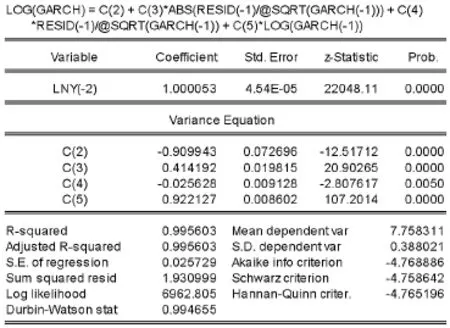
图5 EARCH（1，1）的参数估计结果

上证指数的均值方程：ln（ht）=1.000053ln（ht-2）+et

上证指数的方差方差为：LOG（GARCH）= -0.909942740208+0.414191700579*ABS（RESID（-1）/@ SQRT（GARCH（-1）））-0.0256277858309*RESID（-1）/@SQRT（GARCH（-1））+0.922127445135*LOG（GARCH（-1））

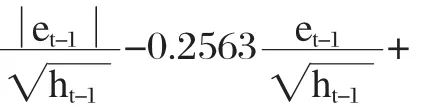
从模型的表达式中可以看出，当一个好的信息冲击对条件方差的对数有一个0.41419-0.02563=0.38856倍的冲击，当一个坏的信息冲击对条件方差的对数有一个0.41419+0.02563=0.43982倍的冲击，说明上证指数显示的杠杆效应是利空消息的冲击比利好消息的冲击更大一点，说明在这段时间内，股市投资人整体上是投机性较强的。

五、结论与策略分析

1、主要结论

从上证指数符合ARCH效应可以推断出其波动的趋势特征为“尖峰厚尾”和聚类特征，通过股指的自相关和偏自相关的分析可以得出波动具有长期拖尾的特点，即上证A股对于利空利好消息具有持久性反应。在拟合时由于GARCH模型的局限性，采用在ARMA基础上建立EGARCH模型较为准确，同时上证A股的杠杆效应使得中国股市存在较大的风险，股民的投资心态和市场的成熟度有待提高。

2、策略分析

国外的证券市场中多为机构投资者，专业的投资机构通常都属于理性的风险厌恶型，我国的证券市场中以个人投资者为多，多属于非理性风险偏好型，看不到股市的泡沫，缺乏规避风险的能力。另外，由于监管部门不完善的监督制度导致一些机构操纵股价，从股市中疯狂套利，使得中小股民损失惨重。这些原因都导致研究分析的杠杆效应是利空消息对股市带来的冲击大于利好消息。

在金融市场中的交易行为，虽然有着独立性的规定，但现实中投机者使用各种方法与外部获得相关，股市中的“跟风”现象反映到波动率上，即为波动率的聚类特征。受到国民经济持续高速增长、新的改革政策出台等利好消息的影响，股指会持续走高；受到清理不良资产、公安部追查恶意卖空、熔断机制等利空消息影响，股指会迅速暴跌，这一系列的现象表明中国股市在走向成熟的道路上困难重重，对每一位投资人的培养任重道远。

[1] 骆殉、吴建红：基于GARCH模型的人民币汇率波动规律研究[J].数理统计与管理，2009，28（2）.

[2] 林德钦：创业板指数波动率预测效果比较研究——基于GARCH族模型[J].金融教学与研究，2014（1）.

[3] 魏正元、张鑫、赵瑜：上证380 高频指数数据已实现GARCH（1，2）模型的风险测量[J].重庆理工大学学报（自然科学），2015（5）.

[4] 周茂华、刘骏民、许平祥：基于GARCH族模型的黄金市场的风险度量与预测研究[J].国际金融研究，2011（5）.

[5] 高铁梅：计量经济学分析方法与建模（第二版）[M].清华大学出版社，2009.

（责任编辑：徐悦）