“导数在研究函数中的应用”教学设计
○教学研究○
“导数在研究函数中的应用”教学设计
王刚陶煜瑾
(江苏省梅村高级中学,214112)
一、教材解读
“导数在研究函数中的应用——单调性”是苏教版《普通高中课程标准实验教科书》数学选修2-2第一章“导数及其应用”的内容.本节是在学生学习了导数的概念、计算、几何意义的基础上学习的内容.学好它既可加深对导数这一概念的理解,又可为深入理解导数的工具性打下基础.由于学生在高一已经掌握了单调性的定义,并能用定义和图象法判定在给定区间上函数的单调性,所以,本节课应该通过初等方法与导数方法在研究函数单调性中的比较,使学生体会到导数法的有效性与一般性,体会高中教材引入导数工具研究函数单调性的必要性.
二、目标定位
根据以上分析,结合《高中数学课程标准(实验稿)》及《江苏省高中数学课程标准教学要求》,本节课确立的教学目标为:
(1)理解导数与单调性的关系,初步掌握用导数法研究函数的单调性;
(2)体会导数方法在研究函数单调性中的有效性与一般性;
(3)感受数学自身发展的一般规律.
教学重点探索导数与单调性的关系及利用导数求函数的单调区间.
难点导数与函数单调性关系的探索过程.
三、教学方法
本节课运用“问题解决”课堂教学模式,采用发现式、启发式的教学方法.通过问题激发学生求知欲,使学生主动参与教学实践活动,在教师的指导下发现、分析和解决问题,总结规律,培养积极探索的科学精神.
四、教学手段
本节课采用多媒体课件等辅助手段以加大课堂容量,通过数形结合,使抽象的知识直观化,形象化,以促进学生的理解.
五、过程设计
1. 创设情境,引出课题
(播放名曲:渔舟唱晚)
问题1气温的变化与我们的生活息息相关,在数学中,我们可以利用函数这一重要的数学模型来研究客观世界的变化.例如,我们可以通过建立气温与时间的函数关系来研究气温的变化趋势.请观察图1中,气温关于时间有怎样的变化趋势?
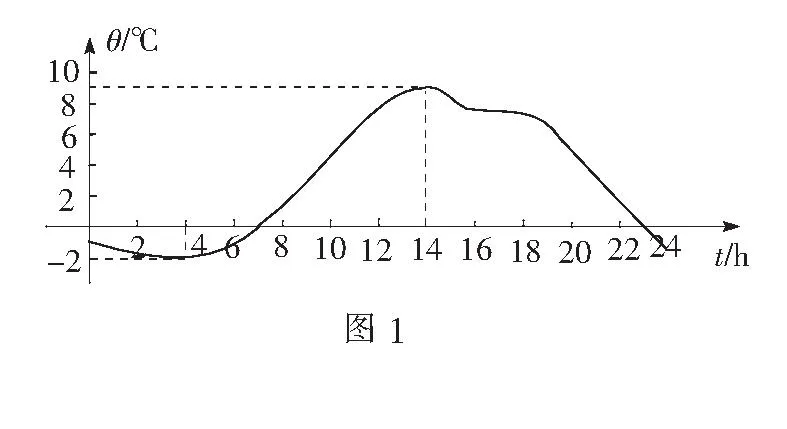
问题2从图1中可以看出,气温随时间的变化有着明显的上升与下降的变化趋势.那么,对于函数图象的这种上升与下降的变化趋势,我们可以用前面所学的哪种知识来加以刻画呢?
设计意图以上案例是必修1函数单调性的引入情境,也是选修2-2导数及其应用章头引言案例.通过该情境,试图沟通必修1与选修2-2在研究函数单调性中的联系.
问题3导数作为函数的变化率刻画了函数变化的趋势,而函数的单调性也是对函数变化趋势的一种刻画.那么,既然它们都是刻画函数变化趋势的数学模型,它们之间又会存在怎样的联系呢?我们能否用导数这一工具来研究函数的单调性呢?
这就是本节课的课题(板书“导数在研究函数中的应用——单调性”).
设计意图这是一个总领整个课堂的问题,试图唤醒学生的原认知结构,打通原有知识之间的联系,引出本节内容.
问题4导数与函数的单调性究竟有什么联系?
著名数学家波利亚曾说过:解决一个数学问题,应该先回到定义.
设计意图为研究导数与函数单调性的关系提供一种研究方法.
2. 师生探究,建构数学
回顾单调增函数的定义.
问题5请同学们观察x2-x1与f(x2)-f(x1)的符号之间的关系.

设计意图定义是数学的根本.通过研究定义从另外一个角度阐述它的含义:说明对区间I上“任意”两点的割线斜率大于零则函数单调递增,这为研究导数与函数单调性关系做好铺垫.
问题7通过几何角度,我们发现割线的斜率与函数的单调性有着紧密的联系.那么,我们如何与导数联系呢?导数的几何意义是什么?
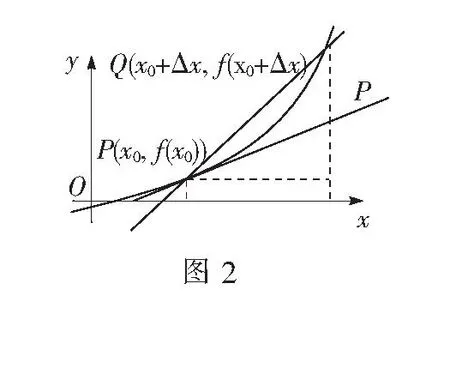
问题9你能从几何角度来解释该定义吗?
设计意图定义是数学的根本,通过研究定义,说明当P,Q两点无限逼近时,割线斜率逼近切线斜率.直观感受割线的斜率是沟通导数与单调性的桥梁(如图3).
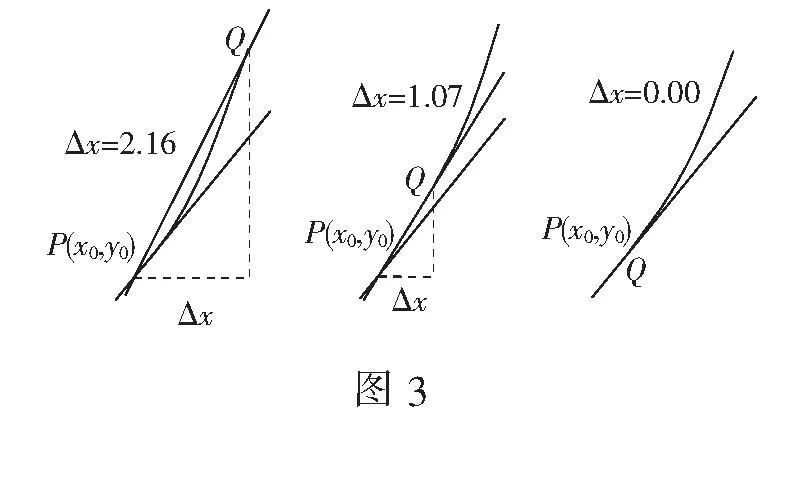
问题10回到刚才的实验,你能发现什么?割线与曲线在点P附近随着Δx→0有着怎样的现象?
(随着点Q沿曲线向点P运动,割线PQ在点P附近越来越逼近曲线,当点Q无限逼近P点时,割线PQ最终成为在点P附近最逼近曲线的直线切线l)
直观感受切线是点P附近最逼近曲线的直线.
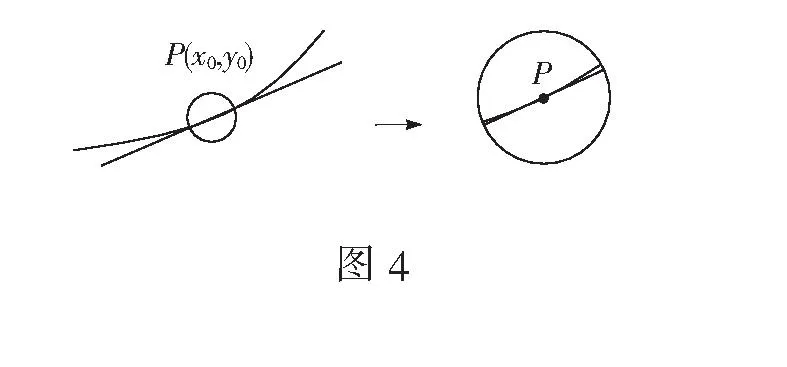
(如图4,放大点P附近的图象,我们可以发现切线与曲线是重合的,此时,我们可以用直线来代替曲线)
导数的本质思想:“以直代曲”,通过这种思想,我们可以将曲线的问题转化到直线上去.例如,在点P附近,我们可以用切线的斜率来刻画曲线经过点P时的上升或下降的“变化趋势”.
问题11f′(x0)______时,曲线经过点P时有上升趋势?
f′(x0)______时,曲线经过点P时有下降趋势?
问题12若点P处的导数符号刻画的是曲线f(x)在点P0处的上升(下降)趋势,那么我们如何用导数来刻画函数在一个区间上的单调性呢?
问题13类比用“任意”两点的割线的斜率来刻画函数的单调性,请思考:
任意x∈(a,b)有______,则函数f(x)在(a,b)上单调递增.
任意x∈(a,b)有______,则函数f(x)在(a,b)上单调递减.
设计意图教材是施教的根本.本段通过课本上的“以直代曲”来解释导数是函数的“瞬时变化率”这个抽象的概念;通过由一点的变化趋势到一个区间的变化趋势,完成对f′(x0)>0到f′(x)>0的解释.
总结导数与函数单调性的关系如下:
一般地,我们有下面结论:
对于函数y=f(x),
如果在某区间上f′(x)>0,那么f(x)为该区间上的增函数;
如果在某区间上f′(x)<0,那么f(x)为该区间上的减函数.
问题14为什么我们要引进导数这一工具来研究函数的单调性呢?
设计意图试图说明导数法在研究函数单调性时的有效性和一般性.
下面我们通过实例来体会导数法在研究函数单调性的有效性和一般性.
3.尝试运用,深化理解
例1确定函数f(x)=x2-4x+3的单调区间.(教师板书)
例2确定函数f(x)=x3-3x的单调减区间.(进行分组竞赛)
设计意图通过教师板演例1,示范用导数求解单调区间的过程;通过例2的学生分组竞赛,说明导数法研究函数单调性的有效性.
例3确定下列函数的单调区间.
(1)f(x)=2x3-6x2+7;
(2)f(x)=xlnx.
设计意图通过学生板演,进一步完善用导数求函数单调性的步骤;并通过实例说明两个注意点:单调区间中不能用“∪”、单调区间为定义域的子区间.通过例3(2)说明导数法在研究函数单调性中的一般性.
总结导数求函数单调区间的步骤:
(1)求函数y=f(x)的定义域;
(2)求导数f′(x);
(3)解不等式f′(x)>0(f′(x)<0);
(4)以上解集在定义域内的部分为单调增(减)区间.
例4请用导数证明f(x)=sinx-x在区间(0,π)上是减函数.
设计意图通过实例,说明导数能简单明了地证明函数的单调性,同时也印证了导数法研究单调性的一般性.
问题15请思考该函数在区间(-π,0)、(-π,π)上的单调性?
问题16请思考该函数在区间(-π,π)上导函数的符号?
问题17结合以上问题判断,函数单调递递减时,f′(x)<0一定成立吗?
问题18结合书本思考题判断,函数单调递增时,f′(x)>0一定成立吗?
结合生活实例"骑自行车"的位移函数单调递增时的两种情况:一是瞬时速度始终大于零;二是瞬时速度大于等于零(即可以出现在前进过程中某些时刻的瞬时速度为零这种情况).
设计意图由实例说明f(x)单调递减(增)时,f′(x)<0(f′(x)>0)不一定成立.
4. 回顾反思,提炼升华
总结本堂课解决的两个问题:
(1)如何用导数来研究函数的单调性(由直观的“形”到抽象的“数”);
(2)为什么要用导数来研究函数的单调性(由特殊的“实例”到一般“结论”).
让学生感受从直观到抽象,从特殊到一般的数学知识的发展规律.
问题19你现在能画出例3(1)函数的图象了吗?
问题20观察该函数图象,思考点f′(0)与f′(2)的值,并思考这两个点的特殊之处.
设计意图通过实例,引出下一节的主要研究方向:极值.
本节课的设计在2015年江苏省青年数学教师优质课评比中获得一等奖,但本节课在教学过程中也存在着一些遗憾.例如,由于时间的关系,例4的作用没能彻底的发挥,没能通过例4在R上的图象说明由函数的单调性判断导数的符号时可以由无数个点处导数为零,但这些点又必须是离散的.

