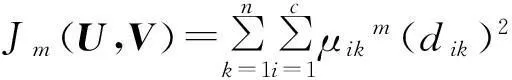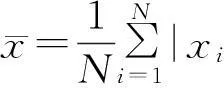粒子群差分扰动优化的聚类算法研究

米　捷，张　鹏，于海鹏

(1.河南工程学院 计算机学院，河南 郑州 451191；2.南召县电业局，河南 南阳 474650)



粒子群差分扰动优化的聚类算法研究

米捷1，张鹏2，于海鹏1

(1.河南工程学院 计算机学院，河南 郑州 451191；2.南召县电业局，河南 南阳 474650)

摘要：通过对大数据优化聚类分析，实现了机械设备的工况监测和故障诊断，提出了一种基于粒子群差分扰动优化的数据模糊C均值聚类改进算法，利用粒子群种群进化的差异度逐渐变小的聚集原理，求得符合分类属性模式的有限数据集特征，使用关联维特征提取方法得到时频聚类交叉项，结合模糊C均值聚类算法，把适应度最小的粒子群个体进行差分进化处理，实现大数据信息流的特征融合和优化聚类.仿真结果表明，采用该算法进行大数据聚类处理，数据聚类中心具有较好的聚焦能力，受到的旁瓣干扰较小，避免陷入局部最优，降低了误分率，在工况识别等领域具有较好的应用价值.

关键词：大数据；聚类；模糊C均值；粒子群

随着计算机信息处理技术的快速发展，人类进入了大数据时代.大数据是通过云计算和云存储方式加工和处理数据，在信息库中，需要对大数据进行有效的挖掘和分类，为数据的特征分析和识别提供前提和基础.大数据的聚类分析就是通过提取数据的规则性信息特征并进行分别，达到物以类聚的效果.优化的数据聚类算法提高了数据处理和信息加工的效率及系统反应的实时性，减少了运算开销，受到了专家的广泛重视[1].

对大数据优化聚类的原理是通过提取数据信息之间的相似性特征并进行特征区分和分类处理，常见的数据聚类算法主要有数据网格层次聚类算法、数据特征风格聚类算法、模糊C均值聚类算法、基于分布式网格粒子群调度的聚类算法等[2].各种聚类算法在不同的应用环境中各有优点，其中基于网格层次的聚类算法分为融合法和分裂法，适合于特征空间维数较高的数据聚类，对聚类中心矢量选择的灵活性较好，但缺点是反复调整聚类的目标状态函数实现收敛，导致计算量较大.K-means聚类算法在数据出现小扰动干扰下，得不到全局最优解，稳定性较差[3].对此，Dunn提出了模糊C均值算法(Fuzzy C-means，FCM).FCM聚类算法利用数据特征之间的模糊性，通过对数据特征之间非此即彼关系的分析，使数据聚类中心不受数据次序的影响，提高了数据的聚敛能力，但FCM算法的缺陷是对初始值聚类中心敏感，容易陷入局部最优解，导致数据聚类的精度不高[4-6].针对上述问题，利用粒子群种群进化的差异度逐渐变小的“聚集”现象，进行大数据聚类中心的差分进化扰动，提出了一种基于粒子群差分扰动优化的大数据模糊C均值聚类改进算法.首先，进行了大数据信息流时间序列模型的构建，对大数据信息流进行特征融合处理，以此为基础，采用粒子群差分扰动方法实现聚类中心的确定和计算，最后通过仿真实验进行了性能验证.

1数据分布结构分析和大数据时间序列模型

1.1大数据的分布式结构分析

为了实现对大数据的优化聚类，首先需要分析大数据在云存储系统中的分布式结构模型.设大数据库的分布式调度的概念格结点G1=(Ma1,Mβ1,Y1)，G2=(Ma2,Mβ2,Y2)，调整聚类中心矢量，两个数据库访问时刻t和t+τ相互关联的初始化聚类中心满足G1⊆G2⟺Y1⊆Y2，令A={a1,a2,…,an}为大数据特征矢量的模糊聚类中心，采用大数据信息流预处理特征序列训练集的属性集，令B={b1,b2,…,bm}为海量数据库特征挖掘的属性类别集，在给定大数据分布的权重指数下，ai的属性值为{c1,c2,…,ck}.需要构建数据库的矢量空间，在矢量空间中进行特征信息流分析，把有限数据集合X分为c类，通过数据预处理和筛选，寻找符合特征模式的有限数据集特征，使用关联维特征提取方法得到时频聚类交叉项，实现数据表示.

把云存储数据库中的有限数据集合X分为c类，得到大数据分布式结构下的属性类别集信息增益表达式：

(1)

(2)

Gain(A)=Info(B)-InfoA(B)，

(3)

式中：A和B分别表示大数据的数据特征类别，pi表示数据信息增益特征分布在A类属性的概率，Info()表示取信息熵并进行卷积运算，计算第i个结点的数据目录，采用广义似然比检验方法对数据特征进行匹配和融合，表示为

C=min{max(Ci)}，

(4)

(5)

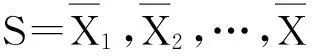
1.2大数据信息流的时间序列分析和预处理

在上述构建的大数据分布式结构模型中，对大数据信息流采用非线性时间序列分析方法进行信息融合和特征提取，在分布式云存储系统中，采用滑动时间窗口采样方法，提取大数据信息流的时间序列为{x(t0+iΔt)}, 其中的i=0,1,…,N-1，分布空间的微簇记为CF=〈F,Q,n,RT1,RT2,RW〉，数据流滑动窗口总数为n，设X和Y为类判别属性集合，在云存储系统中，设t时刻的时序窗口平均测度ε满足2-λt<ε，其中的λ>0，大数据聚类的矢量特征状态空间的相轨迹状态表达式为

X=[x(t0),x(t0+Δt),…,x(t0+(K-1)Δt)]=

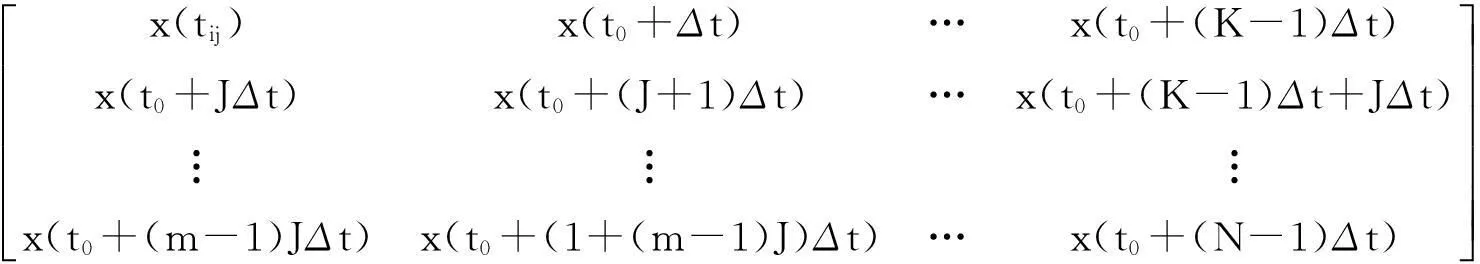
(6)

式中：x(t)表示数据的分布式结构下数据流微簇时间序列，J是相似度特征向量的时间窗函数，m是目标聚类特征空间的最小嵌入维数，Δt为采样时间间隔.进一步，采用粒子群进化方法进行数据的滤波抗干扰预处理.假设在D维大数据聚类搜索空间中有m个粒子组成一个种群，结合FCM聚类算法，得到数据流在聚类过程中的分集聚敛目标函数为

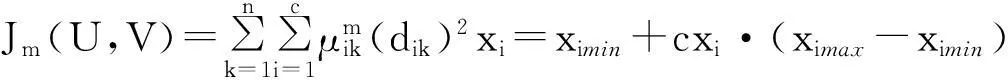
(7)

式中：m为权重指数，xi为聚类中心的第i个矢量， ximax为最大聚敛半径，ximin最小聚敛半径，dik为样本xk与Vi的聚类中心距离.采用欧氏距离计算，结合粒子滤波对聚类特征信息流进行抗干扰信息融合处理，提高了聚类算法的抗干扰能力.

2粒子群差分扰动优化及大数据聚类算法的改进

2.1粒子群差分扰动优化

在进行了大数据聚类的数据结构分析和时间序列模型构建的基础上，对大数据聚类算法进行改进.算法改进的原理如下：为了使数据聚类算法的粒子群差分扰动的全局搜索能力与局部搜索能力达到平衡，利用Logistics混沌映射对粒子群进化种群的聚类中心矢量进行优化搜索，把混沌扰动量引入有限数据集合的粒子群进化种群中，弥补了传统的FCM算法对初始聚类中心有较大敏感性的缺陷.

利用粒子群差分扰动优化聚类进行算法改进的优势体现在：

(1)根据混沌差分进化算法的全局搜索性寻找大数据FCM聚类中心的最佳值，随着聚类中心的更新，把混沌扰动量引入进化种群当中，选出初始最优和全局最优个体，此时算法的寻优能力得到了有效提高；

(2)为了反映数据类群的多样性特征，产生一个随机矩阵作为初始种群，采用粒子群差分扰动序列Logistics混沌映射加入种群中，载入到种群个体中的扰动变量得到最优的适应度值，提高了数据的聚类准确度;

(3)在迭代过程中，为了避免算法过早地进入局部极值部分的点，将粒子群差分扰动理论引入算法中，利用混沌序列的均匀遍历特性和差分进化算法的高效全局搜索能力，有效地克服了算法对初始聚类中心较大的敏感性.

算法的具体实现过程描述如下：利用粒子群种群进化的差异度逐渐变小的“聚集”现象，进行大数据聚类中心的差分进化扰动.假设具有均匀遍历性的大数据分布式数据集为X，由m个粒子构成一个种群，满足最优目标函数下的粒子个体搜索有限数据集

X={x1,x2,…,xn}⊂Rs，

(8)

式中：第i个粒子的当前聚类中心的特征向量xi=(xi1,xi2,…,xiD).在大数据特征空间中，采用协方差搜索方法得到梯度下降方向的数据集合中最优聚类粒子权值

(9)

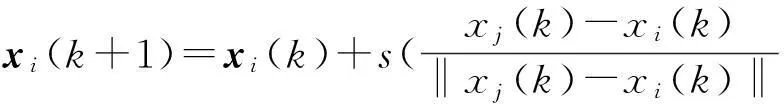
(10)

对于含有n个样本的有限数据集，样本xi(i=1,2,…,n)的聚类中心扰动矢量为

xi=(xi1,xi2,…,xis)T.

(11)

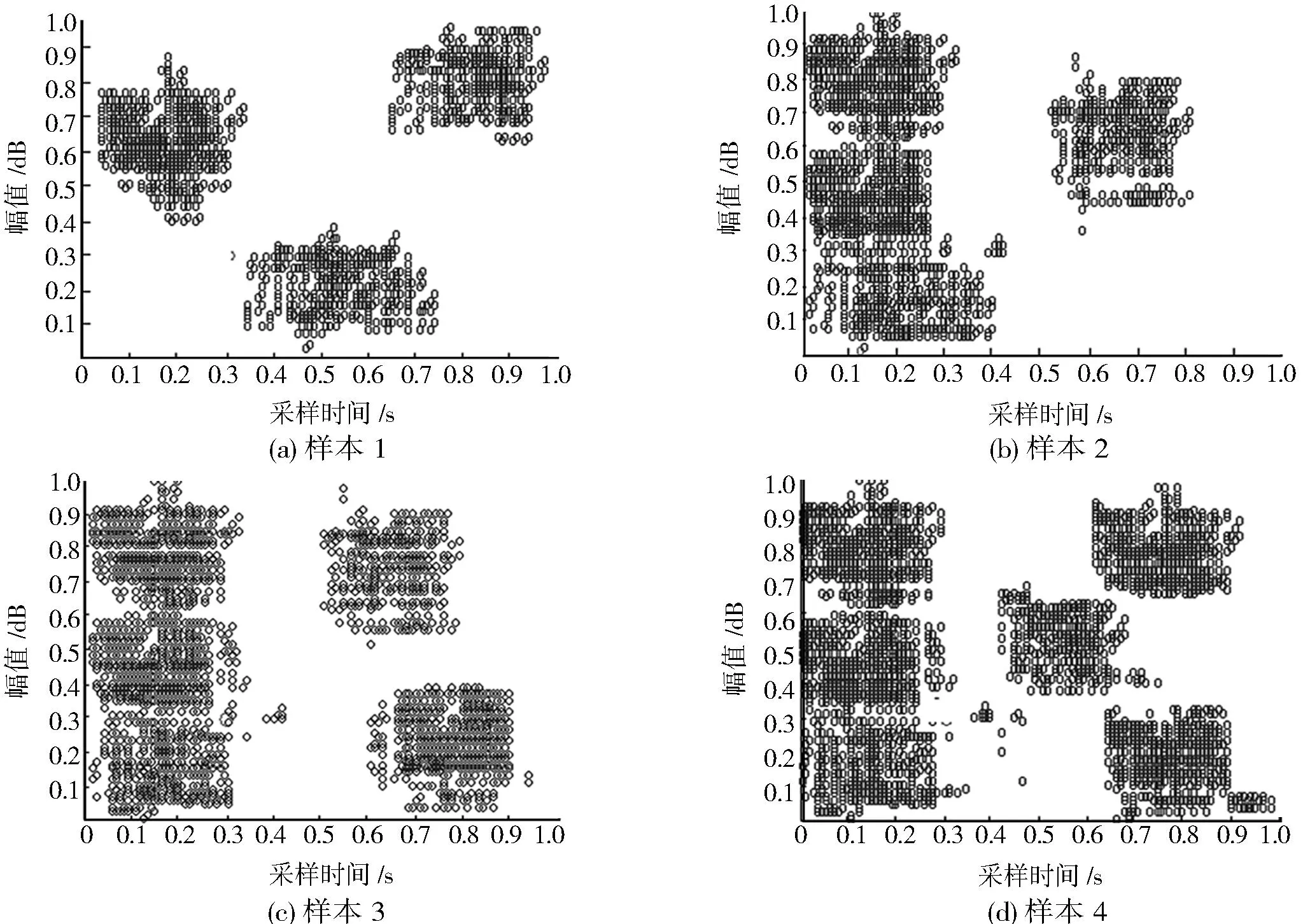
对大数据聚类控制模型进行相位合成，把有限数据集合X分为c类，其中1

V={vij|i=1,2,…,c,j=1,2,…,s}.

(12)

根据个体最优和全局最优解得到第i个聚类中心矢量，从而得到标准粒子群优化下的模糊划分矩阵

U={μik|i=1,2,…,c,k=1,2,…,n},

(13)

式中:c为差分进化的步数，μik为种群类的分岔李雅普诺夫泛函集.为了反映数据聚类过程中粒子群的多样性特征，结合FCM聚类算法，通过定义得到粒子群差分扰动下的聚类目标函数为

(14)

式中:m为聚类包络向量振荡时的极大值，(dik)2为样本xk与Vi的测度距离，用欧氏距离表示为

(dik)2=‖xk-Vi‖2.

(15)

进一步计算大数据聚类的数据类群适应度值为

(16)

采用粒子群差分扰动产生一个初始隶属度矩阵，载入到种群个体中的扰动变量为

xn,G=xn,G+Δxi,

(17)

式中:Δxi为最优个体的迭代步长增量.利用梯度下降信息得到扰动范围NP个混沌序列分量

xn+1=4xn(1-xn),n=1,2,…,NP.

(18)

获取大数据聚类中心稳定阶段前的全局最优点，加入NP个扰动变量的混沌分量：

Δxi=a+(b-a)xn,n=1,2,…,NP.

(19)

为了使大数据聚类算法的粒子群差分扰动的全局搜索能力与局部搜索能力达到平衡，避免陷入约束条件，设置门限值Nth，当Neff

(20)

考虑全局优化问题，在搜索的后期定位适应度最小的个体，并计算粒子群差分扰动个体经历过的最好位置pi=(pi1,pi2,……,piD).通过上述设计，在粒子群差分扰动优化下，使大数据聚类的中心在xi和xj处达到收敛，避免陷入局部最优.

2.2改进算法的实现流程

通过粒子群差分扰动，利用粒子群种群进化的差异度逐渐变小的聚集原理，进行大数据聚类中心的差分进化扰动.根据FCM算法更新模糊分类矩阵，采用粒子群差分扰动方法实现聚类中心的确定和计算，进行数据优化聚类，改进算法的具体流程如下：

(1)初始化大数据聚类中心，计算粒子群种群一定的速度Vi=(υi1,υi2,…,υiD)T和位置Xi=(xi1,xi2,…,xiD)T，对粒子群进行当前位置的更新处理，产生一个随机矩阵作为初始种群，选出初始最优个体和全局最优个体，提取第j个粒子移动的采样均值

(21)

(2)按照差分进化(differential evolution,DE)算法进行粒子群扰动分解，计算第i个粒子全局优化扰动下的聚类中心概率

(22)

式中:xk为第k个动态惯性权重，a为聚类中心的控制参量.

(3)设定相空间搜索维度为m，比较粒子群惯性权重系数，如果满足mf<ξ,则进行第(4)步；如果mf>ξ，则转入第(5)步.

(4)根据不同数据聚类任务，把适应度最小的个体进行差分进化处理，将扰动序列加入粒子群种群中产生模因组信息素矩阵，矩阵大小为c×D维，聚类中心采用归一化处理，收敛到(0,1).若数据集为m，令Aj(L)作为聚类中心，其中j=1,2,…,k.根据Logistic混沌映射形式，聚类矢量特征序列分量

xn+1=4xn(1-xn),n=1,2,…,NP.

(23)

(5)在大数据环境下，对若干样本数据进行归一化处理，调整适应度函数，在分类器中实现数据优化聚类，其中大数据归一化处理过程为

(24)

通过上述处理，以适应度最优解作为最终结果输出，结合对大数据信息流进行特征融合处理的结果，采用粒子群差分扰动提高了对聚类中心的收敛性能和数据聚类的精度.

3仿真实验与结果分析

为了测试本算法在实现大数据优化聚类中的性能，进行仿真实验.采用人工数据集和Web云存储数据库中的DDR3 2014实验数据集进行测试.DDR3 2014实验数据集分为4组样本集合，每类样本属性集有102 498个样本,人工数据集为某大型纺织机械系统工况监测分析专家数据库中的数据样本.设粒子数种群规模为Ns=200,500,700,1 000,对于每一个粒子，通过比较其适应度与群体最优适应度值的大小,根据群体适应度方差得出大数据聚类中心的分布式衰减因子λ=0.25;按照最近邻法则，确定数据集中的聚类划分半径，得出云存储数据库中的中心节点的聚类空间半径R=16;对于每一个粒子，比较它的更新位置和速度，得出群体最优适应度值，把数据聚类的数据点随机划分为某一类，得出粒子位置的阈值μ=10;数据采样样本的时间间隔为0.13s.采用文献[7]给出的虚假最近邻点法，进行相空间搜索维度的最小嵌入维数的计算，得出数据聚类特征空间的维度为30.根据群体适应度方差，设定参量Gmax=30，D=12，c=3，NP=30，扰动范围β=0.001，个体的适应度值T=5，群迭代次数为100，粒子群规模为20，差分进化的阈值为[0.4，0.9]，加速因子为2，粒子群的交叉概率取值为[0,1].采用Web云存储数据库中的DDR3 2014实验数据作为分析样本，得到4个数据库分析样本的聚类结果,如图1所示.

图1　Web数据采样样本大数据聚类结果Fig.1　Data clustering results of Web data samples

图2　人工样本数据采集时域波形Fig.2　Time domain waveform of artificial sample data

从图1可见，采用本算法进行大数据聚类，通过提取数据集的属性特征，采用粒子群差分扰动进行聚类中心估算，实现了4组数据集的特征优化分类，有效降低了误分率.为了进一步验证本算法在实现模式识别和智能诊断方面的应用性能，以实际工作环境中采集的某大型纺织机械系统工况监测分析专家数据库中的数据为分析样本进行数据聚类分析，实现工况模式识别和智能诊断，得到不同数据采集通道上的时域波形,如图2所示.

以上述采集的工况数据为测试样本集，输入本设计的数据聚类系统中进行分析.为了对比算法性能，分别采用本算法和传统算法通过10 000次MonteCarlo运算，得到了大数据聚类中心特征分布结果,如图3所示，从图3可见，采用本算法，聚类中心具有较好的聚焦能力，受到的旁瓣干扰较小，通过粒子群差分扰动抑制了干扰向量，随着数据特征向量的增大，避免了在局部极值点收敛，聚类中心的收敛性较好，有效解决了聚类中心陷入了局部最优的问题.

为了定量分析算法的性能，以大数据聚类的误分率为测试指标，采用本算法和传统算法得到的性能对比结果如图4所示.由图4可知，采用本算法数据聚类的误分率最小、精度较高，提高了状态监测和模式识别的精度，性能优越.

图3　大数据聚类中心特征分布结果Fig.3　Feature distribution results of large data clustering center

图4　性能对比Fig.4　Performance comparison results

4结语

通过大数据优化聚类实现模式识别和状态监测，提出了一种基于粒子群差分扰动优化的大数据模糊C均值聚类算法.研究结果表明，采用该聚类算法能有效提高数据聚类的精度、降低误分率，无论是在云存储环境下的Web数据挖掘还是在实际环境下的纺织机械工况监测等领域，都具有较好的应用价值.

参考文献：

[1]吴涛,陈黎飞,郭躬德.优化子空间的高维聚类算法[J].计算机应用,2014,34(8):2279-2284.

[2]辛宇,杨静,汤楚蘅,等.基于局部语义聚类的语义重叠社区发现算法[J].计算机研究与发展,2015,52(7):1510-1521.

[3]文天柱，许爱强，程恭.基于改进ENN2 聚类算法的多故障诊断方法[J].控制与决策,2015,30(6):1021-1026.

[4]陶新民，宋少宇，曹盼东，等.一种基于流形距离核的谱聚类算法[J].信息与控制,2012(3):307-313.

[5]LIAOLC,JIANGXH,ZOUFM,etal.Aspectralclusteringmethodforbigtrajectorydataminingwithlatentsemanticcorrelation[J].ChineseJournalofElectronics,2015,43(5):956-964.

[6]XINY,YANGJ,TANGCH,etal.Anoverlappingsemanticcommunitydetectionalgorithmbasedonlocalsemanticcluster[J].JournalofComputerResearchandDevelopment,2015,52(7):1510-1521.

[7]李钢虎,李亚安,贾雪松.水声信号的混沌特征参数提取与分类研究[J].西北工业大学学报,2006，24(2):170-173.

Research of data clustering algorithm based on particle swarm differential perturbation optimization

MI Jie1, ZHANG Peng2， YU Haipeng1

(1.CollegeofComputer，HenanUniversityofEngineering，Zhengzhou451191，China;2.NanzhaoCountyElectricPowerBureau，Nanyang474650，China)

Abstract:Through the analysis of large data optimization clustering analysis, the fault diagnosis of mechanical equipment is realized. An improved algorithm for large data fuzzy C means clustering based on particle swarm optimization and differential perturbation optimization is proposed. By using the clustering principle of the population evolution of particle swarm optimization, the finite data set of classification attributes is obtained. Using correlation dimension feature extraction method and FCM clustering algorithm, the population of the adaptive degree is different. Simulation results show that the proposed algorithm is used in large data clustering, and the data clustering center has a good focusing capability, and the side lobe interference is small, which can avoid falling into local optimum, and it can reduce the error rate.

Key words:large data; clustering; fuzzy C means; particle swarm optimization

中图分类号：TP391

文献标志码：A

文章编号：1674-330X(2016)01-0063-06

作者简介：米捷(1981-)，女，河南郑州人，讲师，主要从事计算机应用研究.

基金项目：河南省教育厅科学技术研究重点项目(16A520004)

收稿日期：2015-10-15