基于灰色GM(1，1)模型的河南省老年人口系数预测

万丽颖

(湖北大学 数学与统计学学院, 湖北 武汉 430000)



基于灰色GM(1，1)模型的河南省老年人口系数预测

万丽颖

(湖北大学 数学与统计学学院, 湖北 武汉 430000)

摘要：河南省老年人口绝对量大，位居全国各省之首，分析河南省人口老龄化趋势对经济发展有重要的意义.基于《河南省统计年鉴(2001—2013年)》老年人口系数的数据，采用灰色GM(1，1)模型对老年人口系数进行预测并运用残差检验和后验检验的方法对模型进行检验，结果显示预测的精度并不高.因此，对模型进行改进，采用二次平滑改进的GM(1，1)模型对老年人口系数进行预测，预测结果表明，未来十年内河南省65岁及65岁以上老年人口系数每年都会不同程度上升，故老龄化趋势逐渐上升.最后，对老龄化现象提出了一些对策和建议.

关键词：河南省；GM(1，1)模型；老年人口系数；老龄化

灰色系统理论是在1982年首次提出的，该理论专门研究社会经济现象中小样本、贫信息的不确定系统，目前使用最广泛的灰色预测模型是关于数据预测的一个变量、一阶微分的GM(1，1)模型[1-4].查阅《河南省统计年鉴(2001—2013年)》数据[5]，试图在2000—2012年河南省65岁以上老年人口系数的基础上利用改进的GM(1，1)灰色模型建立河南省老年人口系数预测模型，以期对后10年河南省的人口老龄化趋势做出预测并提出相应的对策[6-8].

1灰色GM(1，1)模型

设时间序列X(0)有n个观察值：X(0)(i)=[X(0)(1),X(0)(2),…,X(0)(n)] X(0)的1-AGO(一次累加生成算子)序列为

X(1)(k)=[X(1)(1),X(1)(2),…,X(1)(n)]，

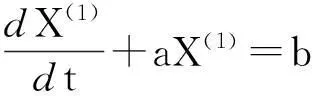
式中：a为发展灰数，b为内生控制灰数，利用最小二乘法可得参数向量

(a,b)T=(BTB)-1BTY.

求解微分方程，可得预测模型：

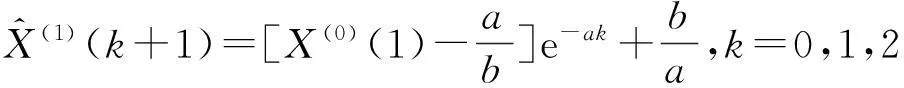
最后，根据公式X(0)(k)=X(1)(k)-X(1)(k-1)可得X(0)的模拟值.

2模型的检验

2.1残差检验

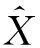
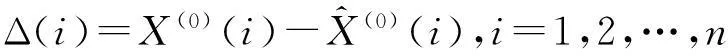
2.2后验检验

计算模型的方差比值C和小误差概率P：

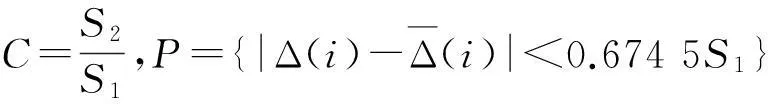
式中:S1为原始序列标准差，S2为绝对误差序列标准差,

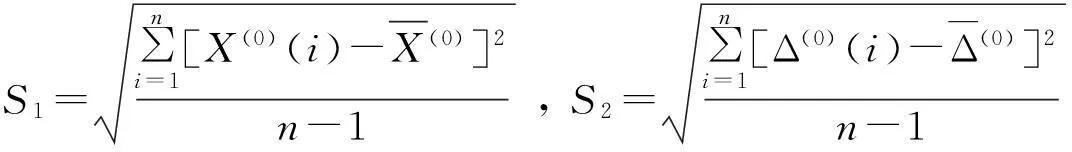
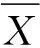
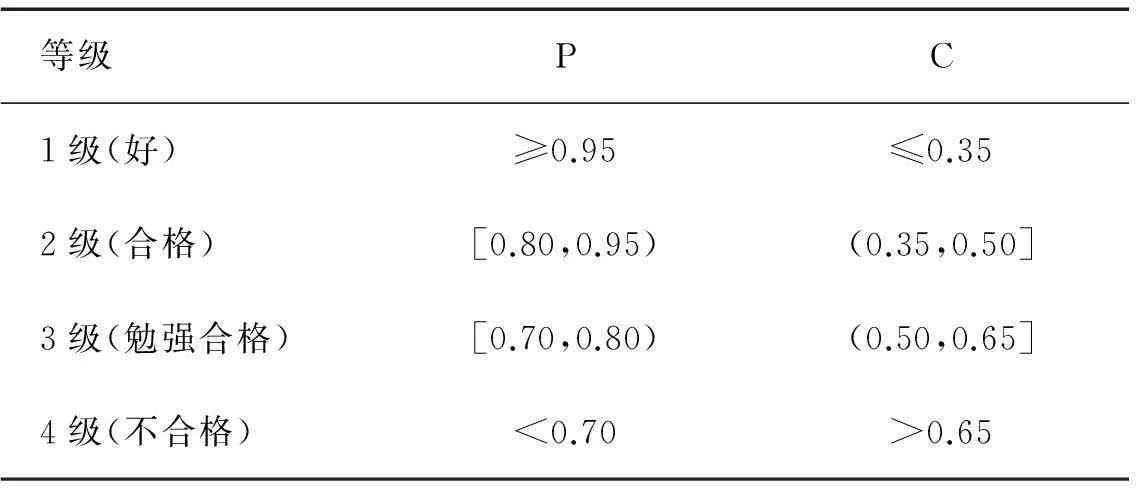
表1　精度检验等级

若是残差检验和后验检验均通过一定的标准，则所建立的模型适合所研究的问题，对未来预测的可信度和精确度较高.

3灰色GM(1，1)模型的平滑改进

典型灰色预测模型GM(1，1)是一种单变量指数增长模型，它具有精度高、所需样本少、计算简便、可检验等优点，但当预测对象不是严格指数持续增长时，模拟误差较大，相应的预测精度会比较低.二次指数平滑可以构造出与原始序列数学期望相同但方差却比原始序列小的新序列，新序列的规律性增强，与灰色GM(1，1)模型结合能够大大提高预测精度，进而可以拓展灰色预测方法的应用范围[10].二次指数平滑的公式为

S′(i)=λX(0)(i)+(1-λ),S″(i)=λS′(i)+(1-λ)S′(i-1),

(1)

3.1河南省老年人口系数的二次指数平滑

人口老龄化程度是随时变化的，另外由于人口数量庞大、流动性强，无法获得精确的数据，这些都属于灰色系统的范畴，所以利用改进的灰色GM(1，1)模型对河南省老年人口系数进行预测.

选择河南省2000—2012年65岁及以上的老年人口系数作为模拟GM(1，1)模型的样本数据，根据样本数据的走势发现其大致呈现指数形式，但短期有较大的波动，指数走势不明显.因此，对原始数据序列进行二次指数平滑，重新生成波动较小的新序列.根据公式(1)对2000—2012年的原始数据进行指数平滑并得到新序列(λ设为0.8)：

S″(i)=[S″(1),S″(2), S″(3), …, S″(13)].

(2)

根据公式(2)得到的数据见表2.根据公式(1)还可以得到还原的预测值序列,见表3.

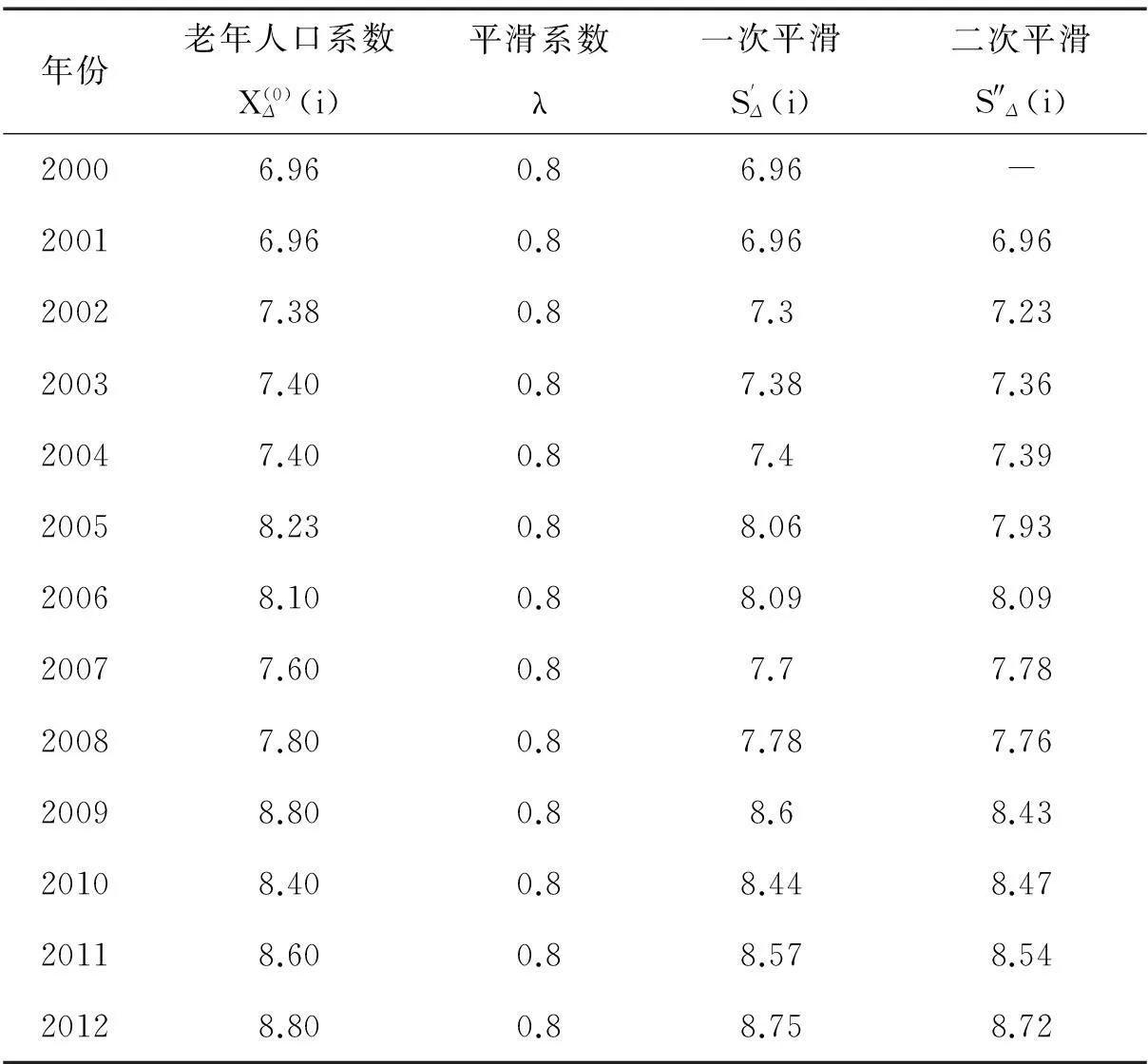
表2　指数平滑新序列

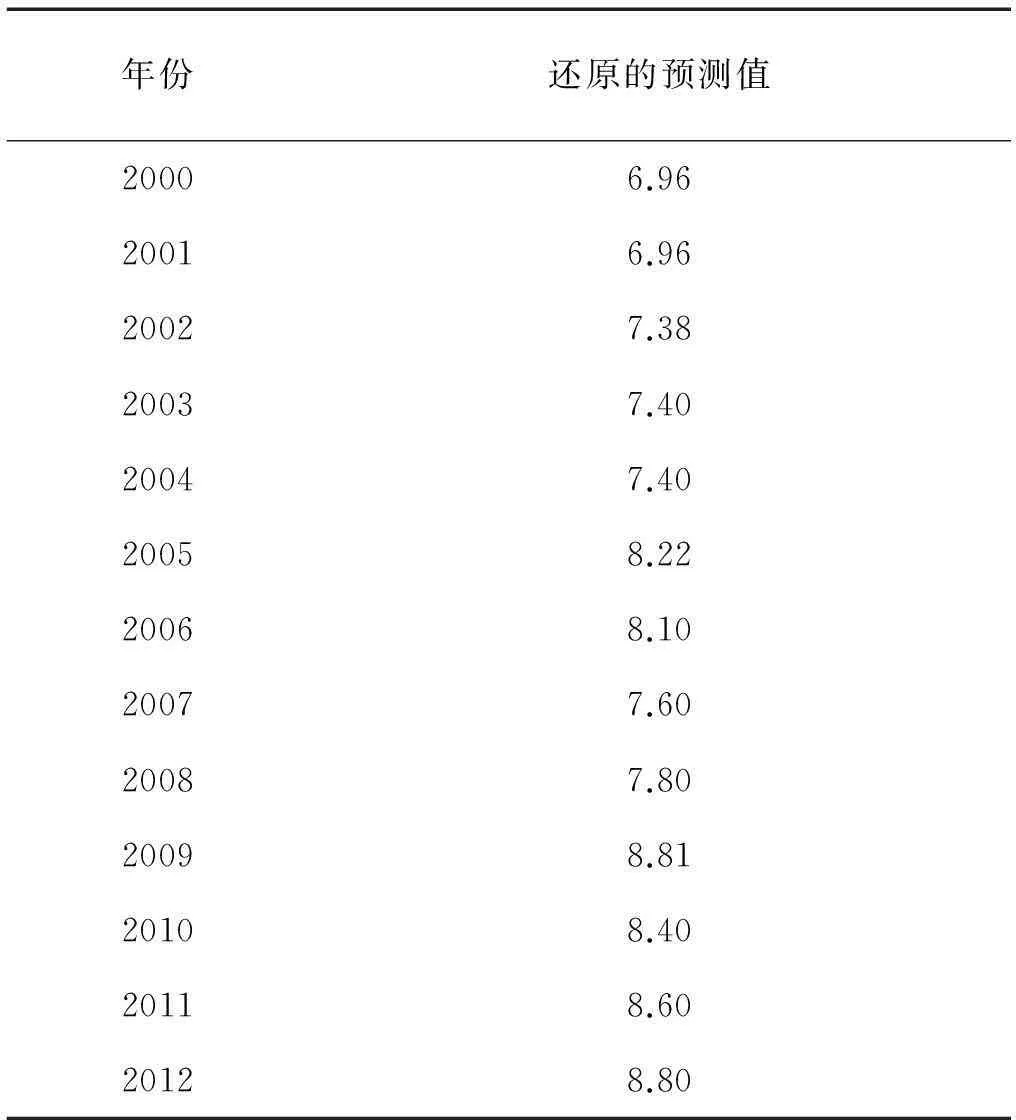
表3　还原的预测值序列

3.2GM(1，1)模型的估计与检验

(1)GM(1，1)估计

对指数平滑的新序列S″(i)作一次累加得到1-AGO序列：

X(1)(i)=[X(1)(1),X(1)(2),X(1)(3),…,X(1)(13)],

根据紧邻均值生成公式：

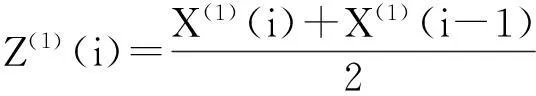
生成紧邻均值序列：

Z(1)(i)=[Z(1)(2),Z(1)(3),Z(1)(4),…,Z(1)(13)],

构造数据矩阵B和数据向量Y，得到参数序列的最小二乘估计为

(a,b)T=(BTB)-1BTY=(0.02,6.88)T.

因此，得到GM(1，1)的白化方程为

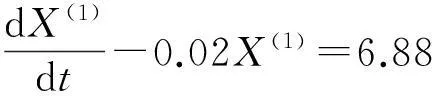
进而得到GM(1，1)离散响应函数为

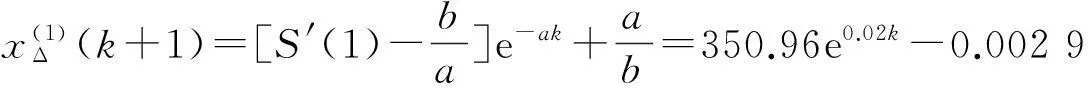
结合S″Δ(1)=S″(1)， 根据公式

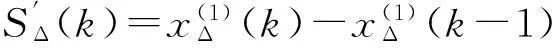
(3)

累减还原生成序列S″(k)的模拟序列S″Δ(k)，模拟序列S″Δ(k)的值见表4.

表4　模拟序列值

(2)GM(1，1)估计结果与检验

根据公式(3)生成2000—2012年的模拟序列S″Δ(k)，预测2013—2023年的数值，并且对模拟序列和预测数据进行指数平滑还原，进而可以进行残差检验，模拟结果及检验结果见表5.

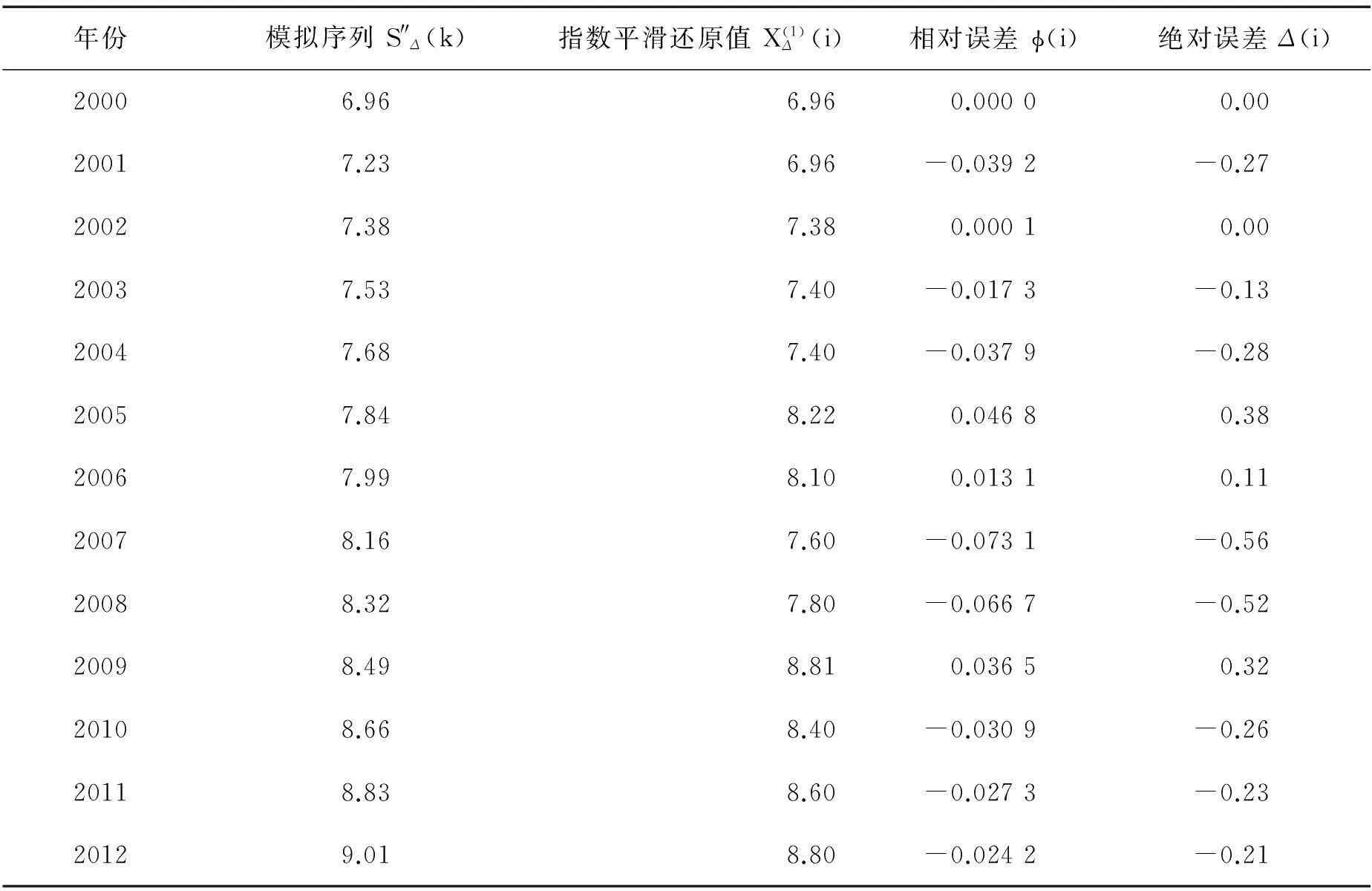
表5　模拟与预测结果

从表5可以看出模拟值只有2007年和2008年的相对误差较大，都大于5%，而其他年份的模拟值的相对误差均小于5%，2002年和2006年的相对误差仅为0.01%和1.31%，平均模拟值的相对误差为1.69%，可见就各样本点而言，二次指数平滑GM(1，1)的模拟效果很好.为了进一步检验模型的整体精度，对模型进行后验检验，根据后验检验的计算方法得到以下结果：

S1=0.654 5， S2=0.284 2， C=0.434 2， P=1.87.

参照精度检验要求可知,后验差比0.350.95，精度属于1级(好).因此,总体上来看模型的拟合效果较好，精度基本达到1级.

4改进的灰色GM(1，1)对老年人口系数的预测

GM(1，1)模型的估计参数a=-0.02<0.3且检验精度达到1级.因此,模型可用于中长期预测，可信度较高.2012年之后的10年，河南省65岁及65岁以上的老年人口系数预测数据见表6.

表6　2012年之后10年的老年人口系数预测

从表6可以看出，2012年之后的10年内，河南省65 岁及65岁以上的老年人口系数每年都在上升，到 2023年将达到11.23%以上，老龄化程度越来越严重.查阅河南省统计年鉴，2013年和2014年全省60岁及65岁以上人口占全省人口总数的比例分别为9.1%和9.4%，上述2013年和2014年老年人口系数的灰色预测值分别为9.2%和9.38%，误差均控制在1%以内，可见模型的预测效果很好.

5结论

河南省人口基数大，老年人口规模将不断壮大,日益增多的老年人口社会抚养和社会照料问题日趋突出.面对严峻的人口老龄化形势，探索既符合社会经济发展水平又切实可行的养老对策，是河南省向前发展的必经之路，也是重中之重,所以要做到科学地认识人口老龄化，大力发展生产力，增强承受人口老龄化的物质力量，逐步建立国家、集体、家庭与个人相结合的社会养老保障体系，走家庭养老与社会养老相结合之路.因此，要完善政策框架，实施积极的养老政策；建立和完善老年护理保险体系；大力发展养老服务业；积极推动城镇化建设，改善农村的养老现状.

参考文献：

[1]刘笠萍.河南省人口老龄化的现状、特征及对策[J].河南商业高等专科学校学报，2004,17(3):73-75.

[2]王献芝.河南省人口老龄化的对策研究[J].河南教育学院学报：哲学社会科学版，2004,23(1):65-67.

[3]王振华.河南省人口老龄化趋势及社会养老保险体系构建[J].经济经纬，2004,5(5):78-79.

[4]王佳.人口老龄化背景下的养老服务产业发展对策研究——以河南省为例[D].武汉：武汉科技大学，2011.

[5]河南省统计年鉴2001—2013年[EB/OL].http：//www.ha.stats.gov.cn.

[6]王小春,王忠莉.河北省人口老龄化趋势预测及对策研究[J].保定学院学报，2013,26(3):26-30.

[7]谢婧,盛利,施学忠.河南省人口老龄化发展趋势预测[J].郑州大学学报：医学版，2008,43(2):289-291.

[8]谢明柱,査奇芬.基于GM(1，1)改进模型的我国农村人口老龄化预测[J].长江论坛，2013,4(4):42-45.

Predication of the coefficient of elderly population in Henan province based on the gray GM(1,1) modle

WAN Liying

(SchoolofMathematicsandStatistics,HubeiUniversity,Wuhan430000,China)

Abstract:The elderly population in Henan province is large, at the top of all the provinces in China. Analyzing the trend of population aging plays an important role in economic development. In this paper, based on the data of Henan statistical yearbook from 2000 to 2012, firstly the grey GM (1, 1) model is adopted to the prediction of coefficient of aging population, and the residual test and posterior test method are used to test the model. The results show that the prediction accuracy is not high, so we try to improve the model, and predict the coefficient of elderly population using the second smooth improved GM (1，1) model. The predicted results show that in the next decade the coefficient of elderly population aged more than 65 and 65 years old will rise in various degree every year, the trend of population aging in Henan province is rising gradually. Finally, I put forward some countermeasures and suggestions for aging phenomenon.

Key words:Henan province; GM(1,1)model; coefficient of elderly population; aging

中图分类号：F222.1

文献标志码：A

文章编号：1674-330X(2016)01-0058-05

作者简介：万丽颖(1990-)，女，河南郑州人，硕士研究生，主要研究统计学及其应用.

收稿日期：2015-11-16