基于扩散模型的京津冀地区空气污染研究

单　欣，朱家明，陆　玉，计　萍

(安徽财经大学 统计与应用数学学院, 安徽 蚌埠 233030)



基于扩散模型的京津冀地区空气污染研究

单欣，朱家明，陆玉，计萍

(安徽财经大学 统计与应用数学学院, 安徽 蚌埠 233030)

摘要：综合分析京津冀地区的空气污染指标数据，首先建立正交因子模型，利用SPSS软件找出京津冀地区主要的污染源及其污染参数，其次结合具体案例分别建立单污染源和多污染源的扩散模型，使用Matlab软件编程，描述了其对周围空气污染的动态影响规律及空气污染浓度的时空梯级分布.

关键词：空气污染；主成分分析；正交因子模型；污染源扩散模型；Matlab

如今，雾霾作为主要的环境污染已经引起了全世界的关注.雾霾天气的形成主要是人为因素造成的，如汽车排放尾气、工厂排放废气和燃放烟花爆竹等，再加上气温低、风力小等自然条件导致污染物不易扩散.本研究以京津冀地区为例,寻找空气污染的主要污染源并建立空气污染的扩散模型.

1数据的获取及假设

本研究的数据来自2015年第十二届五一数学建模联赛B题[1].为了便于解决问题，提出如下假设：①API指标真实可靠，所给数据具有参考统计意义；②单污染源气体初始泄漏时可看作在空中某一点向四周等强度的瞬时释放，在与风向垂直的三维坐标的两个方向上y轴和z轴呈正态分布；③初始时刻污染气体内部温度呈均匀分布，扩散过程忽略热传递、热对流和热辐射；④整个扩散过程中风速的大小与方向保持不变，污染气体的扩散服从扩散定律，即单位时间通过单位法向量面积的流量与它的浓度梯度成正比；⑤假设分析研究的时间段内没有重大的异常天气发生.

2主要污染源及其污染参数的研究

2.1研究思路

根据京津冀地区的数据分析，利用SPSS软件建立正交因子模型[2]，通过污染物因子矩阵可得因子得分函数，由此分析主要的污染源.用主成分分析法将京津冀地区的主要污染物划分为两个层次，利用Matlab软件编程[3]以描述京津冀地区主要污染物的分布情况[4].

2.2正交因子模型

假设污染源由共性因子Fn确定， χ1，χ2，…，χp为可观测指标且E(χi)=μi， εi为X的特殊因子，建立正交模型：

X-μ=AF+ε,

式中:矩阵A为因子的载荷矩阵，aij为第j个因子在第i个指标上的载荷.

首先,将原始数据进行标准化处理[5]，通过相关矩阵R计算特征值和特征向量L.其次,根据累计方差贡献率M来确定因子个数m，累计方差贡献率

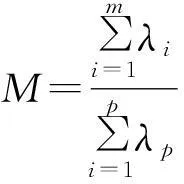
污染物总方差分解表见表1.

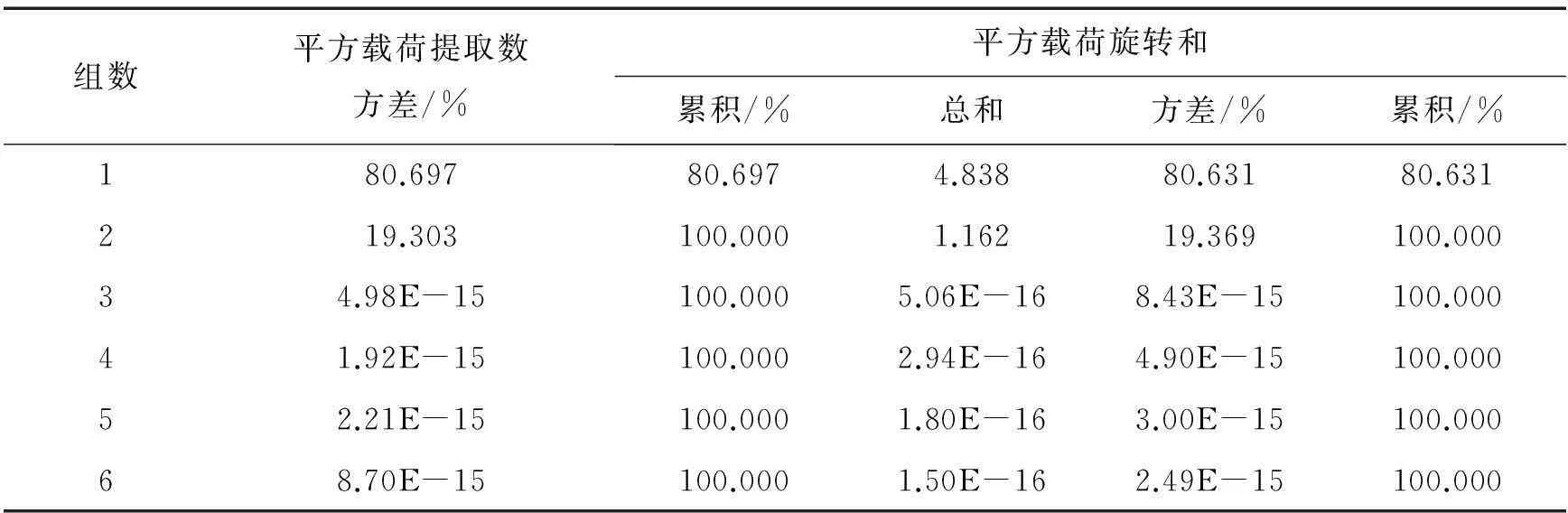
表1　污染物总方差分解表

然后,求得因子载荷矩阵，使用方差最大法对因子载荷矩阵进行正交变换，得出因子得分函数

βj1， βj2， …，βjp中的最大值所对应的污染源为影响因子j的主要污染源[6].污染物因子矩阵见表2.

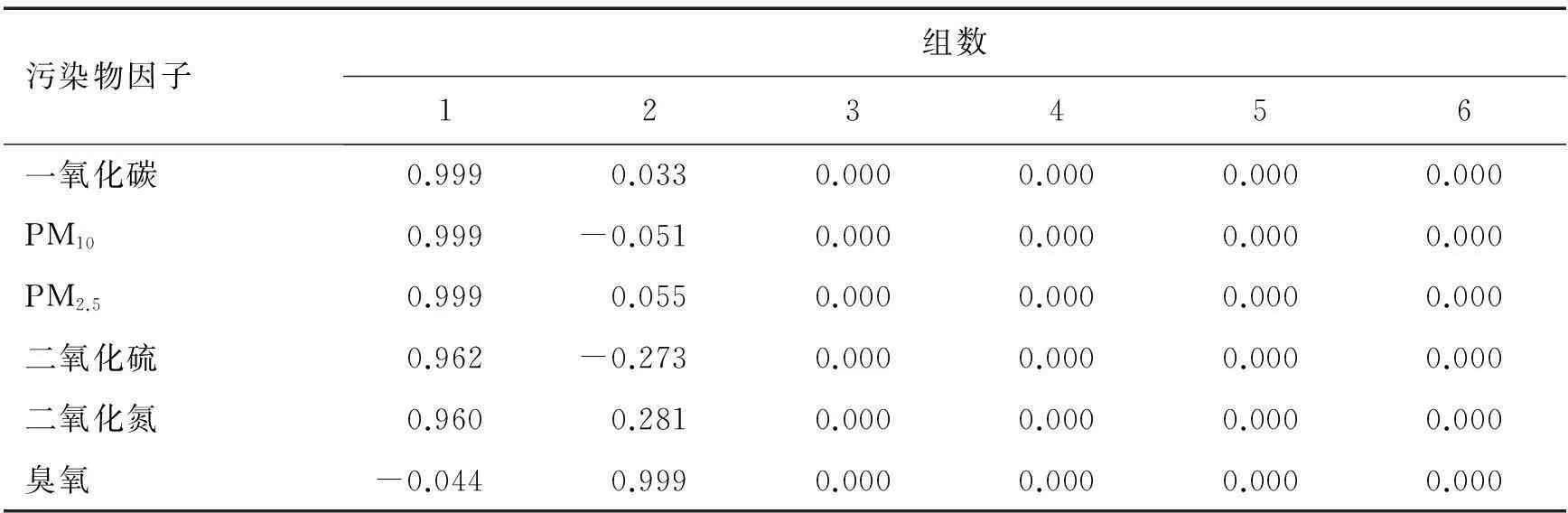
表2　污染物因子矩阵

由表2可知，各个污染物之间的关联性较强，由污染物因子矩阵可得因子得分函数：

F1=0.999[PM2.5]+0.999[PM10]+0.999[NO2]+0.962[SO2]+0.960[CO]-0.044[O3],

由此可知，PM2.5、PM10、二氧化氮、二氧化硫、一氧化碳是京津冀地区的主要污染源.

F2=0.33[PM2.5]+0.051[PM10]+0.055[NO2]+0.273[SO2]+0.281[CO]-0.999[O3]，

由此可知，臭氧是京津冀地区的主要污染源.

综上所述，PM2.5、PM10、二氧化氮、二氧化硫、一氧化碳和臭氧是京津冀地区的主要污染源，可用主成分分析法将其分为一次污染物和二次污染物，前者包括PM2.5、PM10、二氧化氮、二氧化硫、一氧化碳，后者包括臭氧.

用Matlab软件分别绘出北京、天津、石家庄3个城市5种污染气体随时间的变化图，data1～data5分别为PM2.5、PM10、一氧化碳、二氧化氮和二氧化硫的气体质量浓度，具体结果见图1至图3.

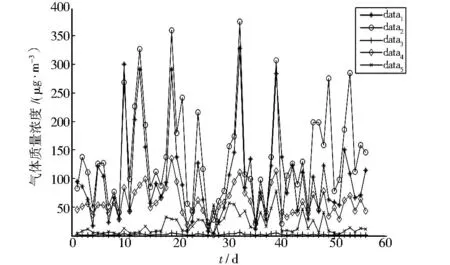
图1　北京污染物分布Fig.1　Distribution of pollutants in Beijing

图2　石家庄污染物分布Fig.2　Distribution of pollutants in Shijiazhuang

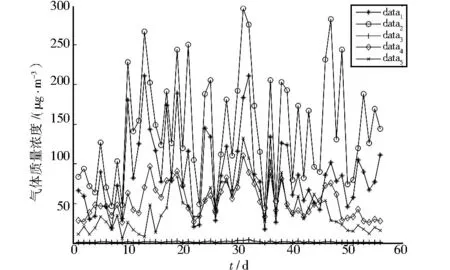
图3　天津污染物分布Fig.3　Distribution of pollutants in Tianjin

由3张趋势图可知，二氧化硫对时间变化最不敏感，PM2.5与PM10对时间变化均较敏感，正好与下面的主成分分析法得到的结果契合.

3污染气体浓度的变化规律

3.1研究思路

假定无风的情况下污染源在大气中匀速向四周扩散的速度为s，建立污染源周边不同距离、不同时段污染物质浓度的预测模型.该问题采用的污染源扩散是点源连续扩散模型，首先在理想的状态下将环境视为一个没有边界的空间，建立单污染源扩散模型，利用质量守恒定律和二阶偏微分方程来描述污染气体浓度的变化规律[7].

图4　单污染源气体的变化规律Fig.4　The change rule of the single pollution source gas

3.2单污染源扩散模型的建立

单污染源气体的变化规律[8]如图4所示.

假设释放时刻记为t=0,释放点选为坐标原点，t时刻无穷空间中(x,y,z)的气体浓度记为C(x,y,z,t).根据假设4，单位时间通过单位法向量面积的流量

q=-σ*gradC，

式中：σ为扩散系数，grad表示梯度，负号表示由浓度高向浓度低的地方扩散.设考察空间域为Ω，Ω的体积为V，包围Ω的曲面为S，S的外法线向量为n,则在[t,t+Δt]内通过Ω的流量

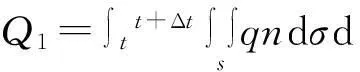
而Ω内放射性气体的增量

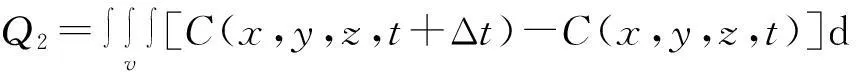
由质量守恒定律可知Q1=Q2,根据曲面积分的奥氏公式可以得到：

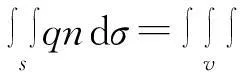
式中div是散度.由此不难得出：

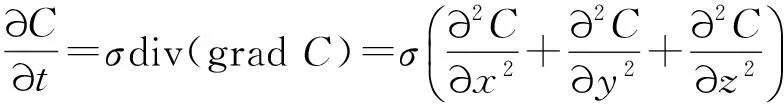
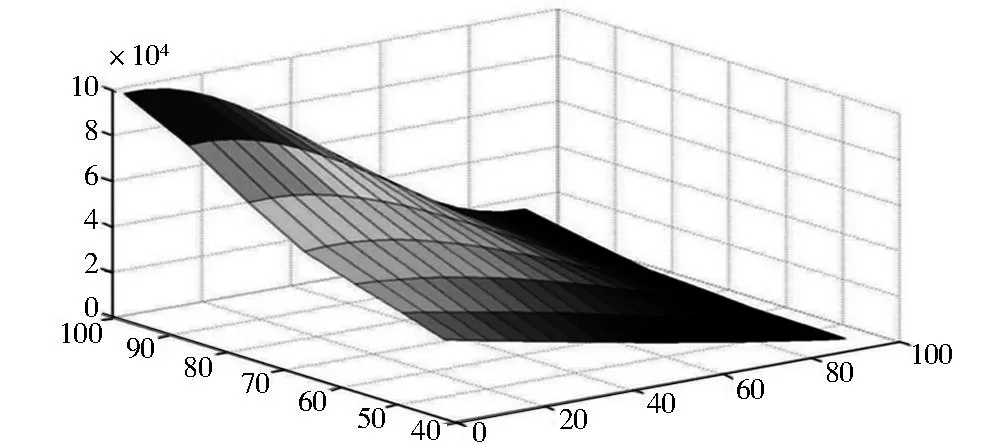
图5　PM2.5扩散模拟图Fig.5　PM2.5 diffusion simulation

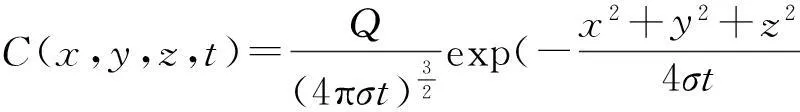
假设风向为东南方,风速为 40km/h,衰减系数为 0.000 01,有效高度为 50m,PM2.5初始质量浓度为各监测点的最高值,利用Matlab模拟[10]可得到PM2.5扩散模拟图.以北京某一监测点为例，结果见图5和表3.由模型结果统计出距离监测点的各个距离段的PM2.5平均减少量,结果见表4.

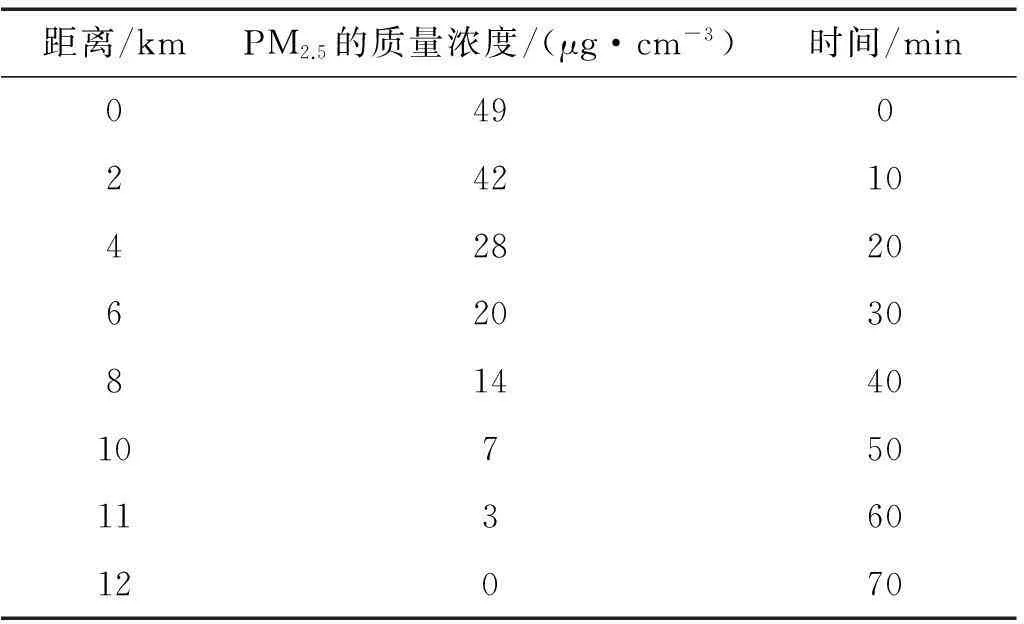
表3　距离对PM2.5质量浓度的影响

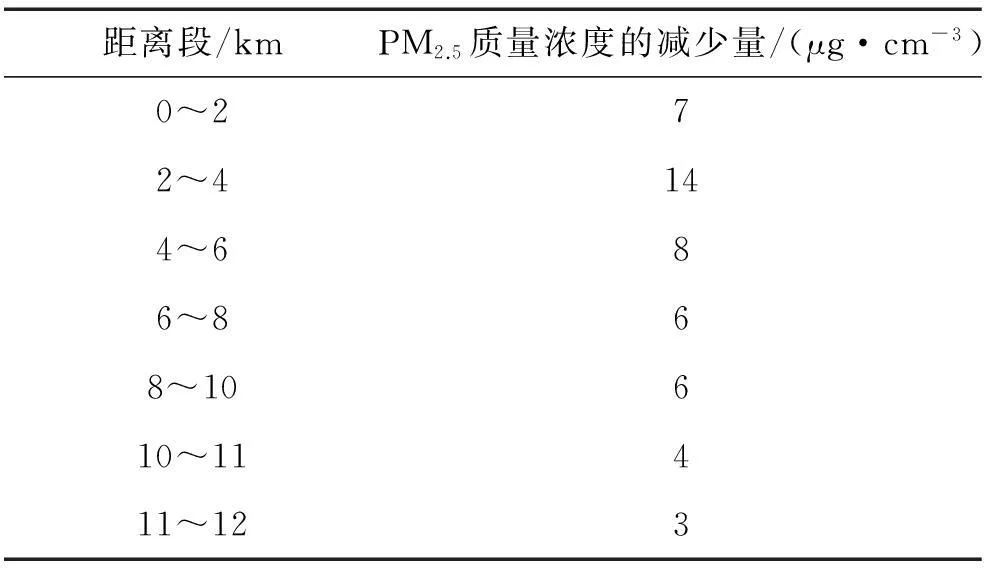
表4　距离监测点各个距离段的 PM2.5质量浓度的平均减少量

由表4可以看到,PM2.5的衰减速度随着与监测站点之间距离的增加先变快后变慢.

4空气污染浓度的时空梯级分布

4.1研究思路

建立多污染源空气污染扩散模型，可根据各个污染源的线性叠加将每一个污染源看作对整个地区空气污染的“贡献”[11].以北京地区为例，利用Matlab软件编程建立线源扩散模型和多污染源空气污染扩散模型来分析空气污染浓度的时空梯级分布.

4.2多污染源扩散模型的建立

首先，建立线源扩散模型，以汽车交通流污染物的线源扩散模型为例.

假设汽车排放的污染物是个无限线源，可以直接采用大气环境质量的线源扩散模型作为汽车流污染物的线源扩散模型，其中污染物的源强采用计算公式[12]

Q=∑Qi=∑EFm×qm×B，

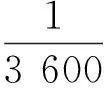
其次，建立多污染源扩散模型.对一个地区的环境空气质量进行评价，一般需要计算研究区域中各个点上的年日平均浓度，要在一个地区多年风向等因素的基础上，将上式进行一定改进，可得到多个污染源的应用模型，该区域的年日平均浓度

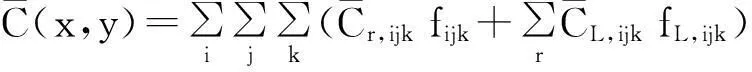
(1)

图6　各污染源对接受点的污染浓度的贡献Fig.6　The contribution of each pollution source to the pollution concentration of the receiving point

以北京地区汽车尾气污染源为例，各污染源对接受点污染浓度的贡献示意图见图6.

首先，假设机动车类型为轿车、微型车、吉普车、中型车并且所有类型的机动车数量是相等的.然后，以北京为例，描述不同道路的车流量及污染物排放情况，见表5与表6.

表5不同道路的车流量及其相关变量

Tab.5Different road traffic flow and related variables

道路长度/km时速/(km·h-1)距市中心距离/km车流量/(辆·h-1)二环32.758430068四环65.380827023六环187.6801724560

表6　不同道路排放源强情况

图7　不同环路不同时间点的空气污染浓度Fig.7　Air pollution concentrations at different times and different time points

根据以上数学模型和北京地区空气污染物的数据可以得到北京市二环路、四环路和六环路在8时、12时和21时空气污染浓度的梯度，见图7.

根据图7，结合表5和表6可以得出离市中心越近的道路空气污染浓度越高并且在高峰期8时左右空气污染浓度达到最大值，21时的空气污染浓度也偏高，相比较而言，12时的空气污染浓度较低.

5结语

结合京津冀地区的具体案例，通过单污染源和多污染源污染物扩散模型的研究，描述了其对周围空气污染的动态影响规律及空气污染浓度的时空梯级分布，模型可推广应用于农业上的花粉传播、工业上有害气体的扩散、工业材料的渗透与融合等方面的研究.

参考文献：

[1]2015年第十二届五一数学建模联赛B题[EB/OL].http://www.saikr.com/cumcm/2/2476.html.

[2]张文波，陈红艳.实用数据统计分析及SPSS 12.0应用[M].北京：人民邮电出版社，2006.

[3]胡守信，李伯年.基于Matlab的数学实验[M].北京：科学出版社，2004.

[4]周兆源，张时煌.京津冀地区气象要素对空气质量的影响及未来变化趋势分析[J].资源科学，2014(1):191-199.

[5]任建标.数据、模型与决策[M].北京：中国财政经济出版社，2004.

[6]杨桂元，黄己立.数学建模[M].合肥：中国科学技术大学出版社，2008.

[7]姚丽萍，王远飞.基于MPI的大气污染扩散模型的并行计算研究[J].计算机工程,2005(22)：54-57.

[8]牛文胜,孙振海.大气扩散模式的简要回顾[J].气象科技,2000(2):1-2.

[9]邬毅敏.基于GIS的大气点源污染高斯烟羽扩散模拟研究[D].上海：华东师范大学，2010.

[10]张韵华.MATHEMATICA符号计算系统实用教程[M].合肥:中国科学技术大学出版社，1998.

[11]吴建国.数学建模案例精编[M].北京:中国水利水电出版社，2005.

[12]黄汉明，刘幕仁，韩仲志，等.城市交通汽车尾气扩散与分布建模仿真[J].云南大学学报：自然科学版，2005，27(5A)：256-261.

Air pollution in Beijing-Tianjin-Hebei region based on diffusion model

SHAN Xin, ZHU Jiaming, LU Yu, JI Ping

(InstituteofStatisticsandAppliedMathematics,AnhuiUniversityofFinanceandEconomics，Bengbu233030,China)

Abstract:Aiming at the problem of air pollution, comprehensive analysis is carried out for air pollution index data of Beijing, Tianjin and Hebei province. firstly the orthogonal factor model is set up, using SPSS software to identify the main pollution sources and pollution parameters in Beijing, Tianjin region. Secondly, a single pollution source and multi pollution source diffusion model are established combined with the specific case, using Matlab software programming. The model describes the dynamic impact of the surrounding air pollution and air pollution concentration of time and space.

Key words:air pollution; principal component analysis; orthogonal factor model; pollution source diffusion model; Matlab

中图分类号：O212.4

文献标志码：A

文章编号：1674-330X(2016)01-0052-06

作者简介：单欣(1993-)，女，河北沧州人，本科生，研究方向为经济统计.通信作者：朱家明(1973-)，男，安徽泗县人，副教授，研究方向为应用数学与教学建模.E-mail:zhujm1973@163.com.

基金项目：国家自然科学基金(11301001);安徽财经大学教研项目(acjyzd201429)

收稿日期：2015-10-27