柱体绕流的CIP方法模拟

赵西增，付英男，张大可

(1. 浙江大学 海洋学院，浙江 杭州 310058; 2. 国家海洋局第二海洋研究所 卫星海洋环境动力学国家重点实验室,浙江 杭州 310012)



柱体绕流的CIP方法模拟

赵西增1，2，付英男1，张大可1

(1. 浙江大学 海洋学院，浙江 杭州 310058; 2. 国家海洋局第二海洋研究所 卫星海洋环境动力学国家重点实验室,浙江 杭州 310012)

摘要：柱体绕流和流致振动现象是一个复杂的工程问题，利用自主研发的CIP-ZJU模型，对低雷诺数(Re<300)圆柱和方柱绕流问题开展了数值模拟。模型在直角坐标系统下建立，采用紧致插值曲线CIP方法作为流场的基本求解器离散了Navier-Stokes方程，基于多相流的理论实现流-固耦合同步求解，利用浸入边界方法处理固体边界。模拟结果与文献结果进行比较，二者吻合情况较好。通过引入压力阻力项和摩擦阻力项，分析了Strouhal数、阻力系数、升力系数等参数随雷诺数的变化情况。结果表明，圆柱绕流与方柱绕流在水动力参数的变化规律上存在多处差异。

关键词：柱体绕流；CIP方法；Navier-Stokes方程；浸入边界法；Strouhal数

钝体绕流，特别是柱体绕流问题在工程实际中经常遇到，如风吹过高层建筑物、海水流过石油钻井平台、海流流经海洋立管等。其共同的特点是，在一定雷诺数范围内，粘性流体流过柱体结构物时，会发生边界层的分离，进而对结构物产生周期性作用。因此，准确计算出流体对柱体结构的作用荷载及其在荷载作用下的动力响应，具有重要的科学价值和工程意义。

许多学者采用试验方法和数值模拟方法开展了钝体绕流问题的研究。Tritton[1]在实验室内通过观察石英试管的弯曲度得到Re在0.5～100范围内圆柱绕流的阻力，与理论值吻合良好。Kawaguti等[2]对Re在1～100圆柱绕流问题进行了数值模拟，并考虑了压力和摩擦力对阻力的贡献，结果表明压力阻力项在阻力中占有主导地位。Rajani等[3]利用二阶精度的中心差分格式对对流方程进行离散，对圆柱绕流进行了二维和三维数值模拟，将两者的涡脱频率和升力系数进行对比，发现大于某一临界雷诺数时，二维结果偏大，三维效应不可忽略。方柱绕流也是钝体绕流的一种典型形式。Okajima[4]研究了不同类型的矩形柱体的涡旋脱落频率，并指出Strouhal数是雷诺数的函数。Sohankar等[5]引入二阶精度的Van Leer迎风格式对对流项进行求解，指出Re>50时会有稳定的卡门涡街产生。Breuer等[6]将格子玻尔兹曼方法(lattice Boltzmann method，LBM)和有限体积法 (finite volume method，FVM)分别应用到二维方柱绕流数值模拟中，两种方法的计算结果显示了较好的一致性。Sen等[7]利用有限元方法(finite element method，FEM)对Re<150时的方柱绕流进行二维数值模拟，发现最初的分离点是在基点处而不是在后角点处。潘小强等[8]利用Fluent分别模拟了二维圆柱和方柱绕流的流场情况，结果表明同样雷诺数的圆柱和方柱绕流，圆柱绕流更易得到稳态非定常解。周云龙等[9]采用FVM模拟了二维圆柱和方柱的流动分离状态，发现两者最大的不同点在于分离点的不同，圆柱绕流没有固定分离点而方柱绕流固定分离点在其前后角点处。不同柱体绕流过程中的水动力特性的差异，仍未明朗，这将是本文工作的重点。

本文采用自主研发的CIP方法模型[10-11]，通过浸入边界方法处理流-固耦合问题，对不同雷诺数(Re<300)的圆柱绕流和方柱绕流问题进行数值模拟，并通过与文献结果的比较验证模型的有效性。为了得到稳定的流场信息，本文采用了与传统差分格式不同的高阶格式CIP方法对N-S方程进行了离散，该方法通过对网格内结点函数值及其导数值联立，实现了三阶精度的差分求解对流方程，具有格式稳定和低耗散性的特点；同时，在直角网格系统内，通过引入浸入边界方法，有效处理了流-固耦合问题，可有效避免动态网格系统中的大量信息交换，保证了模型的计算效率，为进一步模拟运动物体做好准备。本文将从多个角度分析圆柱绕流与方柱绕流的区别。

1数学模型的建立

1.1控制方程

本流场模型以二维N-S方程为控制方程，其矢量形式为

(1)

(2)

为了把CIP方法应用于对流方程，对方程(2)取空间导数，可得到

(3)

模型在直角笛卡尔系统下建立，采用多相流理论处理固-液的相互作用，满足下面的控制方程：

(4)

式中：m=1, 2,φ1为液体相，φ2为固体相，在一个网格内满足φ1+φ2=1。固体相的处理基于浸入边界方法得到，将在下面的部分给出解释。网格内的流体特性可用下式来表示：

(5)

式中：λ为密度ρ或者粘性系数μ。

1.2数值方法

1.2.1CIP方法

CIP方法是Takewaki等[12]于20世纪80年代中期提出并发展起来，用于求解双曲型偏微分方程的一种有效的数值计算方法。其基本原理是基于空间网格点的变量值及其空间导数值，利用三次多项式进行插值近似，反演出网格单元内部变量的真实信息，得到三阶精度的显式格式。为了更好地解释CIP方法，考虑简单的常系数一维对流方程：

(6)

式中：u为大于零的常数。此类偏微分方程可用不同差分方法求解。下面将给出CIP方法的工作原理。图1(a)～(c)给出了一阶迎风差分方法的工作原理，对于一阶差分格式来说，它利用直线的方式联立相邻两个节点的信息来工作，而忽略了网格内部的信息，导致较大的数值耗散。为了真实再现网格内部的信息，有必要求助高阶差分方法，而对于常规高阶差分的建立需要更多的网格点的信息。CIP采用一种独特的方式，在一个网格内实现了高阶差分格式，通过利用空间网格点的变量值及其空间导数值，来描述该网格内的信息，可真实再现网格内的信息。

通过对方程(6)求关于x的偏导，得到如下的空间导数方程：

(7)

(8)

在n+1时刻的单元格剖面函数fn+1可以通过将n时刻的剖面函数fn平移-u△t得到，函数f和g的时间演变可以通过下面的拉格朗日变换得到

(9)

图1　CIP方法的基本原理Fig. 1　Principle of CIP method

图2　半拉格朗日方法的CIP格式Fig. 2　CIP method of semi-Lagrangian format

(10)

CIP方法采用一种独特的方式，在一个网格内实现了高阶差分格式，使得本文的数值模型可以应用于复杂流动问题的模拟，这也是本文所采用的差分方法与其他方法的不同之处。

1.2.2时间积分

采用分步算法对动量方程进行时间积分。首先忽略扩散项和压力项，只考虑对流项的中间速度；其次求解扩散项；然后求解压力方程，计算下一时间步的压力；最后考虑压力梯度项，计算速度的最后值。设△t为时间步长，在t=n△t到t=(n+1)△t时刻的计算时间内，具体的时间积分过程如下：

1) 对流项(I)：

(11)

通过CIP方法[13]可得到方程的解：

(12)

式中：‘*’为对流项计算结束后的中间时间标志。

2)非对流项(I):

扩散项的计算：

(13)

扩散项的时间离散采用显示格式，中间速度可表示为下面的形式：

(14)

其中,方程(14)的空间离散采用中心差分格式。

3)非对流项(II):

压力和速度的匹配:

(15)

通过对方程 (15)第一行公式取散度，并引入连续方程，可得到如下形式的泊松方程：

(16)

泊松方程的求解通过SOR迭代得到。

考虑动量方程的压力梯度项，计算速度的最终值，计算式为

(17)

根据式(4)、(5)和(18)更新界面和网格内流体信息，然后返回到步骤1，这样就完成了整个计算过程，一直到设定的步骤结束。

1.2.3固体边界处理

采用浸入边界法(immersedboundarymethod)[14]处理固体对流场的影响:

(18)

式中：ufn+1为在欧拉坐标体系中通过式(17)计算得到的“局部”流场速度；Ubn+1为通过拉格朗日方法得到的固体速度[15]，本文中柱体静止，固体的速度设定为零；un+1为二者耦合作用的“整体”速度，这样就得到了流-固耦合流场的求解。上述方法也可称为固体体积流-固耦合处理方法。基于浸入边界方法的流-固耦合技术，采用固定网格，在计算过程中无需更新网格，可保证模型的高效率，使得模型在处理大位移的流固耦合计算中具有强大优越性。本文采用的方法具有较易实施的优势，方便模型向三维拓展。

1.3参数定义

升力Fl为

(19)

式中：Re为雷诺数,Cd为阻力系数,Fd为阻力,Cl为升力系数,St为Strouhal数,上角标p和v分别表示由于压力和摩擦力所产生的阻力或升力，Sij=(∂ui/

∂xj+∂uj/∂xi)/2。

1.4数值模型

计算区域及网格划分如图3和图4所示。圆柱与方柱的特征长度均为D=1m，上游边界距离柱体中心7.5D，下游边界距离柱体中心22.5D，两侧边界距离柱体中心均为7.5D。为了捕捉柱体周围的复杂流动，柱体近壁面采用细网格。

图3　圆柱、方柱绕流计算区域示意图Fig. 3　Sketch of the computational domain

图4　圆柱、方柱绕流网格示意图Fig. 4　Sketch of the computational mesh

1.5边界条件和初始条件设置

计算流场的边界条件以及初始条件设置如下：初始条件：初始设定一个从左向右的速度场，u=U0，v=0；其中，u、v分别为x、y方向的速度；初始压力场都设定为零。边界条件：来流边界保持为均匀来流速度U0；出口边界条件，开边界；柱体表面边界条件：无滑移边界，即un=0；两侧壁面：自由滑移边界。

2模型验证及数据分析

2.1网格收敛性分析

为验证模型的有效性及网格收敛性，采用三套网格对Re=100时圆柱绕流进行模拟。三种网格从网格1到网格3，最小网格分别为0.04、0.02和0.01m，模拟结果如表1所示。由于网格1的网格尺寸较大，Cd值与文献结果相差较为明显，而网格2与网格3误差较小。考虑到计算效率和精度，选择网格2对下文其他工况进行模拟。

2.2圆柱绕流参数分析

下面对Re=1～300的圆柱绕流进行模拟，结果如表2所示。从表中可看出，Re<50时，没有漩涡脱落，St数为零。

表1　网格数据及主要参数对比

表2不同Re圆柱绕流主要参数结果

Table 2Main parameters of flow around a cylinder at differentRe

ReCdSt113.4—54.53—103.11—202.18—301.81—401.59—501.470.131601.440.139801.370.1571001.330.1661201.320.1751401.3250.1821601.3150.1852001.3250.1922501.330.1993001.350.206

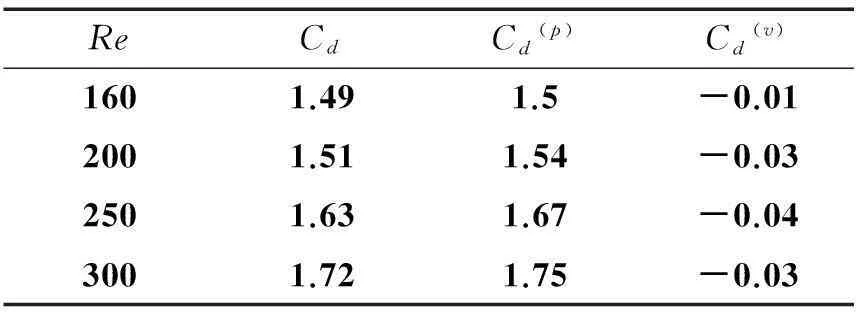
图5给出了圆柱绕流主要水动力参数随Re的变化情况。在Re<40时，没有漩涡脱落为层流状态，如图5(a)所示在开始段Cd骤减，主要是因为4

图5　主要参数随Re的变化Fig. 5　The variation of main parameters vs Re

图6给出了50100时由于考虑到实际情况的三维效应，数模的二维结果会高估St数。主波长λ为卡门涡街一侧前后2个涡之间的距离，如图7所示，λ与St数的关系可近似表示为λ/D=1/St[22]。由图可知随着Re的增大，λ呈单调下降趋势，卡门涡街漩涡之间的距离越来越小。

2.3方柱绕流参数分析

下面将对Re<300情况下的方柱绕流进行模拟，结果如表3所示。与圆柱绕流结果类似，本文模拟出的结果在Re<50时显示没有漩涡脱落，依旧为层流，St数值为零；而在Re=50时，不稳定状态首次显现，伴随有漩涡脱落，流动转化为非层流，说明在Re=40～50，漩涡开始脱落，与Sohankar等[23]通过数值模拟测得的Re=52较为接近。

图6　Strouhal数和主波长λ随Re的变化曲线Fig. 6　The variation of Strouhal number and primary wavelength vs Re

图7　主波长λ示意图Fig. 7　Sketch of primary wavelength

Table 3Main parameters of flow around a cylinder at differentRe

ReCdSt114.1—54.85—103.28—202.33—301.95—401.74—501.6250.116601.5650.126801.510.1361001.490.1431201.480.1471401.4850.151601.490.152001.510.1432501.630.1363001.720.136

图8　主要参数随Re的变化Fig. 8　The variation of main parameters vs Re

ReCdCd(p)Cd(v)1601.491.5-0.012001.511.54-0.032501.631.67-0.043001.721.75-0.03

与圆柱绕流类似，在Re<40时，是层流状态。图8(a)给出了Cd、Cd(p)、Cd(v)的变化，可发现整体趋势相同，最后近似发展为3条平行的直线，与Sen等[7]在2100时，与毕继红等[25]的结果相差较小，与其他文献相差较大，其中的影响因素较多，像离散方法不同、计算域的大小、边界条件设置的不同均可导致计算结果的误差。在Re≈140时，阻力系数达到极小值，此时分离点由后角点处转移到前角点处(本文将此时定义为“转折点”，方便后文叙述)，使得方柱侧面受力发生变化，导致Cd(v)的合力方向发生变化，在Re<140时，Cd(v)数值为正；而如表4所示，在Re>140时，Cd(v)数值为负，方向发生了变化，这也是方柱绕流与圆柱绕流最大的区别之一。由图8(c)可看出方柱绕流中，压力阻力项仍然占有主导地位，且随着雷诺数的增大，摩擦阻力项相比于压力阻力项基本可以忽略。从图8(d)中可以看出在Re≈140时，升力系数的增长率逐渐减小，这也是分离点变化导致的结果，过了转折点之后，升力系数的增长率变大，结果与现有文献吻合良好。从图8(e)可看出St数的变化趋势与现有文献基本一致，在转折点处达到最大值，而数值方面的误差可能由多种原因导致，Breuer等[6]指出阻塞比的增加会导致St数的增大。主波长λ的变化与St数相反，先减小再增大，在转折点处的主波长达到最小。

2.4圆柱与方柱绕流参数对比

为了清晰说明圆柱绕流与方柱绕流的区别，将结果中的重要参数进行对比。

图9给出了圆柱、方柱绕流主要水动力参数随Re的变化曲线。由图9(a)可以看出，Cd mean随Re的变化趋势大体一致，在Re<10时，Cd mean随Re的变大急剧减小，然后趋于平稳，且方柱的阻力系数大于圆柱，这是两者形状不同所导致的。两者在Re≈140～150达到极小值，此时方柱的分离点由后角点转移到前角点，方柱摩擦阻力的方向发生变化，而圆柱没有此现象发生，其分离点只围绕一点往复运动，且摩擦阻力保持为正值，方向不变。图9(b)给出了圆柱和方柱Cl max随Re的变化曲线。在Re<150时，两者的大小基本一致，经过转折点之后，方柱的升力系数显著增大，大体呈线性增长，分离点在前角点时，方柱两侧面将受到附面涡的作用，使得升力增大，而圆柱不存在此现象，升力系数变化相对平稳。图9(c)给出了圆柱和方柱St随Re的变化曲线，圆柱的St随着Re的增大呈单调上升趋势，而圆柱的St先增加，在转折点处到达极大值，后随着Re的增大而减小。方柱的St值一直小于圆柱的St值，这也说明方柱的漩涡脱落频率比圆柱的漩涡脱落频率小。图9(d)给出了圆柱和方柱λ/D随Re的变化曲线。可看出，圆柱绕流的主波长随着Re的增大而单调下降，而方柱绕流的主波长先随着Re的增大先下降再上升，在转折点附近到达极小值，且方柱绕流的主波长一直大于圆柱绕流的主波长。

图9　圆柱绕流与方柱绕流参数对比Fig. 9　Comparison between flow around a cylinder and a square cylinder

图10(a)、(b)给出了圆柱、方柱阻力和升力系数振幅随Re的变化。可看出，升力系数的振幅比其对应的阻力系数的振幅大一个数量级，两者均随着Re的增大而增大，且在方柱绕流的转折点之前，圆柱和方柱的阻力升力系数振幅大体一致，转折点之后，方柱的阻力升力系数振幅显著增大，圆柱的变化依旧平缓，且方柱的振幅大于圆柱的振幅。图10(c)给出了Cd(p)/Cd(v)随Re的变化曲线，可看出Cd(p)相比于Cd(v)一直处于主导地位，且随着Re的增大越明显。圆柱绕流Cd(p)/Cd(v)随Re呈线性增长，而方柱绕流Cd(p)/Cd(v)随Re呈非线性增长，随着Re的增加，变化率越来越大，且在方柱绕流中，Cd(p)的主导地位相对圆柱绕流要明显。

图10　主要参数随Re编号曲线Fig. 10　The variation of main parameters vs Re

3结论

本文利用自主研发的CIP-ZJU模型，对低雷诺数(Re<300)圆柱和方柱绕流问题开展了数值模拟。模型在直角坐标系统下建立，采用紧致插值曲线CIP方法作为流场的基本求解器，离散了Navier-Stokes方程,利用浸入边界方法处理固体边界，基于多相流的理论实现流-固耦合同步求解。分别分析了圆柱和方柱绕流的绕流水动力特性，并将两者的主要水动力参数进行比较，得出如下结论：

1)圆柱和方柱绕流的Cd在Re≈140～150达到极小值，此时方柱的分离点由后角点转移到前角点，方柱的摩擦阻力的方向发生变化，而圆柱没有此现象发生，其分离点只围绕一点往复运动，且摩擦阻力保持为正值。

2)圆柱绕流的Cd(p)、Cd(v)均为正值，而方柱绕流在转折点之后，由于分离点的变化，导致摩擦阻力的合力方向发生改变，Cd(v)变为负值。

3)方柱绕流的St值一直小于圆柱绕流的St值，说明方柱的漩涡脱落频率比圆柱的漩涡脱落频率小。相反方柱绕流的主波长大于圆柱绕流的主波长。

4)圆柱绕流与方柱绕流升力系数的振幅比其对应的阻力系数的振幅大一个数量级，两者均随着Re的增大而增大，且在方柱绕流的转折点之前，圆柱和方柱的阻力升力系数振幅大体一致，转折点之后，方柱的阻力升力系数振幅显著增大，圆柱的变化依旧平缓，且方柱的振幅大于圆柱的振幅。

本文的计算结果与文献结果吻合良好，验证了此方法的可行性，为进一步探讨柱体形状对绕流阻力的影响，开展流致振动等研究打下良好基础。

参考文献：

[1]TRITTON D J. Experiments on the flow past a circular cylinder at low Reynolds numbers[J]. Journal of fluid mechanics, 1959, 6(4): 547-567.

[2]KAWAGUTI M, JAIN P. Numerical study of a viscous fluid flow past a circular cylinder[J]. Journal of the physical society of Japan, 1966, 21(10): 2055-2062.

[3]RAJANI B N, KANDASAMY A, MAJUMDAR S. Numerical simulation of laminar flow past a circular cylinder[J]. Applied mathematical modelling, 2009, 33(3): 1228-1247.

[4]OKAJIMA A. Strouhal numbers of rectangular cylinders[J]. Journal of fluid mechanics, 1982, 123: 379-398.

[5]SOHANKAR A, DAVIDSON L, NORBERG C. Numerical simulation of unsteady flow around a square two-dimensional cylinder[C]//Proceedings of the Twelfth Australasian Fluid Mechanics Conference，1995.

[6]BREUER M, BERNSDORF J, ZEISER T, et al. Accurate computations of the laminar flow past a square cylinder based on two different methods: lattice-Boltzmann and finite-volume[J]. International journal of heat and fluid flow, 2000, 21(2): 186-196.

[7]SEN S, MITTAL S, BISWAS G. Flow past a square cylinder at low Reynolds numbers[J]. International journal for numerical methods in fluids, 2011, 67(9): 1160-1174.

[8]潘小强, 袁璟. CFD软件在工程流体数值模拟中的应用[J]. 南京工程学院学报: 自然科学版, 2004, 2(1): 62-66.

PAN Xiaoqiang, YUAN Jing. Numerical simulation of engineering fluid by using CFD software[J]. Journal of Nanjing institute of technology: Natural Science Edition, 2004, 2(1): 62-66.

[9]周云龙, 邓冬, 刁成东,等. 方柱绕流和圆柱绕流旋涡脱落的数值模拟[C]//中国工程热物理学会2008多相流学术会议论文集. 青岛, 2008: 086020.

ZHOU Yunlong, DENG Dong, DIAO Chengdong et al. Numerical simulation of vortex shedding from a square and circular cylinders[C]// Conferences of multiphase flow of Chinese Society of Engineering Thermophysics. Qingdao, 2008: 086020.

[10]赵西增. 一种自由面大变形流动的CFD模型[J]. 浙江大学学:工学版, 2013, 47(8): 1384-1392.

ZHAO Xizeng. CFD modeling of distorted free surface flow[J]. Journal of Zhejiang university: engineering science, 2013, 47(8): 1384-1392.

[11]ZHAO Xizeng, YE Zhouteng, FU Yingnan, et al. A CIP-based numerical simulation of freak wave impact on a floating body[J]. Ocean engineering, 2014, 87: 50-63.

[12]TAKEWAKI H, NISHIGUCHI A, YABE T. Cubic interpolated pseudo-particle method (CIP) for solving hyperbolic-type equations[J]. Journal of computational physics, 1985, 61(2): 261-268.

[13]YABE T, XIAO Feng, UTSUMI T. The constrained interpolation profile method for multiphase analysis[J]. Journal of computational physics, 2001, 169(2): 556-593.

[14]PESKIN C S. Flow patterns around heart valves: A numerical method [J]. Journal of computational physics, 1972, 10(2): 252-271.

[15]HU Changhong, KASHIWAGI M. Two-dimensional numerical simulation and experiment on strongly nonlinear wave-body interactions[J]. Journal of marine science and technology, 2009, 14(2): 200-213.

[16]WILLIAMSON C H K. Defining a universal and continuous Strouhal-Reynolds number relationship for the laminar vortex shedding of a circular cylinder[J]. Physics of fluids, 1988, 31(10): 2742-2744.

[17]SCHLICHTING H, GERSTEN K, KRAUSE E, et al. Boundary-layer theory[M]. Berlin: Springer, 1968.

[18]余化军. 圆柱和方柱绕流及矩形柱涡激振动的二维数值模拟分析[D]. 天津: 天津大学, 2011: 17.

YU Huajun. Two dimensional numerical analysis of flow over a circular and square cylinder and vortex-induced vibration of rectangular cylinder[D]. Tianjin: Tianjin University, 2011: 17.

[19]吕林. 海洋工程中小尺度物体的相关水动力数值计算[D]. 大连: 大连理工大学, 2006: 66-67.

LYU Lin. Numerical simulations for the hydrodynamics of small scale objects in ocean engineering[D]. Dalian: Dalian University of Technology, 2006: 66-67.

[20]ZDRAVKOVICH M M. Flow around circular cylinder[M]. Oxford: Oxford Science Publications, 1997.

[21]HE J W, GLOWINSKI R, METCALFE R, et al. Active control and drag optimization for flow past a circular cylinder: I. oscillatory cylinder rotation[J]. Journal of computational physics, 2000, 163(1): 83-117.

[22]VOROBIEFF P, GEORGIEV D, INGBER M S. Onset of the second wake: dependence on the Reynolds number[J]. Physics of fluids, 2002, 14(7): 53-56.

[23]SOHANKAR A, NORBERG C, DAVIDSON L. Low-Reynolds-number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition[J]. International journal for numerical methods in fluids, 1998, 26(1): 39-56.

[24]GERA B, SHARMA P K, SINGH R K. CFD analysis of 2D unsteady flow around a square cylinder[J]. International journal of applied engineering research, 2010, 1(3): 602-610.

[25]毕继红, 余化军, 任洪鹏. 静止方柱和圆柱绕流的二维数值分析[J]. 三峡大学学报: 自然科学版, 2012, 34(1): 41-45.

BI Jihong, YU Huajun, REN Hongpeng. Two dimensional numerical simulation of flow over a static square cylinder and a static circular cylinder[J]. Journal of China Three Gorges university: natural sciences, 2012, 34(1): 41-45.

Numerical simulation of flow past a cylinder using a CIP-based model

ZHAO Xizeng1，2, FU Yingnan1, ZHANG Dake1

(1. Ocean College, Zhejiang University, Hangzhou 310058, China; 2. Second Institute of Oceanography, SOA State Key Laboratory of Satellite Ocean Environment Dynamics, Hangzhou 310012, China)

Abstract：Flow past a cylinder and the flow-induced vibration phenomenon are complex engineering problems. We developed a CIP-ZJU (constrained interpolation profile-Zhejiang University) model to study the flow past circular and square cylinders for Reynolds numbers Re< 300. The model was established in the Cartesian coordinate system, using the CIP method as the base flow solver to discretise the Navier-Stokes equations. The fluid-structure interaction was treated as multiphase flow, with liquid and solid phases solved simultaneously. We used an immersed boundary method to deal with the boundary of the solid body. We then compared our computations with available results and obtained good agreements. By introducing pressure and viscous drags, we analyzed the variations in the Strouhal number, drag coefficient, and lift coefficient with the Reynolds numbers. Results show that the variations of the dynamic characteristics differ between the flows past circular and square cylinders.

Keywords：flow past cylinder; CIP method; Navier-Stokes equation; immersed boundary method; Strouhal number

中图分类号：O352

文献标志码：A

文章编号：1006-7043(2016)03-297-09

doi:10.11990/jheu.201411003

作者简介：赵西增(1979-), 男, 副教授, 博士生导师；付英男(1990-),男，硕士研究生.通信作者：付英男, E-mail:fyn_zju@163.com.

基金项目：国家自然科学基金资助项目(51209184, 51479175).

收稿日期：2014-11-02.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160104.1427.002.html

网络出版日期：2016-01-04.