山区高墩大跨度连续刚构桥稳定性与参数影响分析

唐峰，李德建

(1.中交四公局第二工程有限公司,北京 101149；2.中南大学 土木工程学院，湖南 长沙 410075)



山区高墩大跨度连续刚构桥稳定性与参数影响分析

唐峰1，李德建2

(1.中交四公局第二工程有限公司,北京 101149；2.中南大学 土木工程学院，湖南 长沙 410075)

摘要:以山区某高速公路高墩大跨度连续刚构桥为工程实例，对其在最高墩阶段、最大悬臂阶段和成桥阶段的线弹性稳定性进行计算，找出稳定安全系数最低的阶段。在此基础上，对其进行非线性稳定分析，讨论非线性因素对稳定性的影响，探讨相关参数如混凝土强度等级、桥墩纵向尺寸、双肢薄壁桥墩间距、系梁设置、基础刚度对稳定安全系数的影响，并得出结论，研究成果可为高墩大跨度连续刚构桥的设计与施工提供参考。

关键词：高墩；大跨度；连续刚构桥；稳定性；施工阶段；非线性

近年来，随着高速公路建设不断向山区延伸，我国高墩大跨度连续刚构桥得到很大发展，建造技术已达到世界领先水平，并进一步向薄壁、高墩、大跨方向发展，这使得稳定问题日益突出，若处理不当，桥梁结构可能会发生整体或局部失稳而使结构丧失承载力[1-4]。因此，有必要对高墩大跨度连续刚构桥的稳定性进行研究，以保证结构的安全。尤其是对高墩大跨度连续刚构桥各典型施工阶段进行分析，找出稳定性最不利施工阶段，并对其进行弹塑性稳定性分析，得出其真实的稳定安全系数，用以指导设计和施工，就显得尤为重要。本文以布林大桥为工程背景分析高墩大跨度连续刚构桥的线弹性稳定以及非线性稳定，并对稳定的影响参数进行讨论。布林大桥为贵州山区跨越山区峡谷的一座高墩大跨度连续刚构桥，跨径布置为105 m+200 m+105 m，最高墩为1号墩，其墩高为127.6 m 。主墩墩身采用双肢变截面矩形空心墩，肢间净间距850 cm，纵向每肢外侧均按200∶1放坡，横向根据墩高采用分段放坡形式，从上到下分别采用80∶1和50∶1共2种坡率。空心墩壁厚90 cm，且壁厚沿墩高保持不变。桥梁总体布置见图1，1号墩构造见图2。

图1　布林大桥桥型布置图Fig.1 Layout drawing of Bulin Bridge

图2　1号高墩构造图Fig.2 Structure diagram of No.1 pier

1线弹性稳定分析

1.1有限元模型的建立

利用大型桥梁专业分析软件Midas-civil的空间梁单元模型对布林大桥的3个典型阶段的线弹性稳定进行分析，即最高墩的自体稳定性、最大悬臂阶段的稳定性和成桥阶段的稳定性。

布林大桥的主墩采用C55混凝土，主梁采用C60混凝土。模型中的边界条件按如下处理：

最高墩阶段：墩底与承台固结，墩顶自由。

最大悬臂施工阶段：墩底与承台固结，墩顶与箱梁底固结，最大悬臂两端自由。

成桥阶段：主墩墩底与承台固结，墩顶与箱梁底固结，边跨梁端约束为铰结，即约束其竖向、横向的线自由度和横向转角自由度，释放其他方向的自由度。

计算分析时考虑恒载(一期恒载以及二期恒载)、活载、施工荷载和纵桥向以及横桥向的静风荷载的组合。

1.2最高墩阶段的线弹性稳定计算

对布林大桥127.6 m高墩达到最大墩高时的线弹性稳定问题进行分析，考虑以下3种工况。

工况1：自重；

工况2：自重+横向风荷载；

工况3：自重+顺桥向风荷载。

通过Midas-civil的线弹性屈曲分析，得到布林大桥达到最高墩阶段的线弹性稳定安全系数和对应的屈曲模态如表1所示。

表1最高墩阶段的线弹性稳定安全系数及对应的屈曲模态

Table 1 Linear elastic stability safety coefficient and buckling mode at the stage of completion of pier construction

计算工况安全系数λ对应的屈曲模态工况122.53纵向屈曲工况222.53纵向屈曲工况322.52纵向屈曲

从表1可以看出，3种工况的第1类线弹性稳定安全系数都大于4，根据受压柱结构弹性稳定安全系数的规定[5]，该阶段的稳定性满足规范要求，在各种工况下的屈曲模态都表现为纵向屈曲。

1.3最大悬臂阶段的线弹性稳定计算

计算荷载：1)桥墩自重；2)由于浇筑误差，引起一侧主梁自重增加4%，另一侧减少4%；3)挂蓝、施工机具和现浇块件的动力效应，一端取1.2，另一端取0.8，挂蓝自重取800 kN;4)挂蓝一侧跌落，取动力放大系数为2；5)施工材料堆放荷载，取一悬臂承受8.5 kN/m的竖向均布荷载，并在其端头作用200 kN的竖向集中力，另一悬臂空载；6)横桥向风荷载；7)顺桥向风荷载。

当挂蓝正常工作时，计算以下3种工况的稳定性。

工况1：1)+2)+3)+5)

工况2：1)+2)+3)+5)+6)

工况3：1)+2)+3)+5)+5)

当挂蓝跌落时，计算以下3种工况的稳定性。

工况4：1)+2)+4)+5)

工况5：1)+2)+4)+5)+6)

工况6：1)+2)+4)+5)+7)

计算结果如表2所示。

表2最大悬臂阶段线弹性稳定安全系数及对应的屈曲模态

Table 2 Linear elastic stability safety coefficient and buckling mode at the stage of the largest cantilever

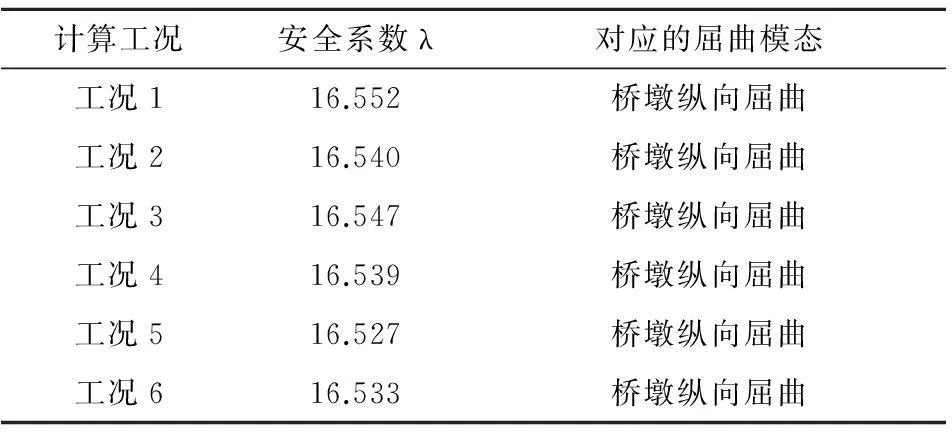
计算工况安全系数λ对应的屈曲模态工况116.552桥墩纵向屈曲工况216.540桥墩纵向屈曲工况316.547桥墩纵向屈曲工况416.539桥墩纵向屈曲工况516.527桥墩纵向屈曲工况616.533桥墩纵向屈曲

从以上结算结果可以看出，最大悬臂阶段的稳定安全系数较最高墩阶段降低了27%左右，但稳定安全系数仍然远大于4。

1.4成桥阶段的线弹性稳定计算

成桥阶段的稳定分析考虑的荷载有：自重、二期恒载和汽车活载。

计算以下2种工况。

工况1：自重+二期恒载

工况2：自重+二期恒载+全桥满布汽车活载

计算结果如表3所示。

表3成桥阶段线弹性稳定安全系数及对应的屈曲模态

Table 3 Linear elastic stability safety coefficient and buckling mode at the stage of completion of the whole bridge

计算工况安全系数λ对应的屈曲模态工况118.02桥墩纵向屈曲,主梁竖向弯曲工况217.50桥墩纵向屈曲,主梁竖向弯曲

从表3可知，全桥合龙完成后，结构的约束增强，成桥阶段的稳定安全系数均较最大悬臂阶段大，该阶段也具有足够的稳定安全系数。

从以上3个典型阶段的线弹性稳定分析可知，最大悬臂阶段在工况5荷载作用下的稳定安全系数最小，故以下的非线性稳定分析及稳定性影响参数分析均是以此工况下最大悬臂阶段为讨论分析的。

2非线性稳定分析

结构的线弹性稳定计算是基于结构的刚度较大，荷载引起的位移较小且结构的本构模型为线弹性模型这样一个假定进行的。但是对于高墩大跨连续刚构桥，其薄壁空心墩的刚度较小，在重力、施工荷载、风荷载及初始缺陷的作用下，墩顶可能会发生较大的偏位，部分材料可能已经进入弹塑性状态或已达到极限强度，这时结构的稳定性分析应考虑几何非线性和材料非线性的影响。

2.1零缺陷作用下几何非线性稳定计算

假定材料为线弹性，利用Midas-civil建立空间梁单元，对最大悬臂阶段的几何非线性稳定进行计算，计算结果如表4所示。

表4　几何非线性稳定安全系数

从以上计算结果可以看出，计入几何非线性后，稳定安全系数的变化幅度在10%以内，这说明结构的刚度较大，几何非线性对稳定的影响不大，这主要是由于假设的材料为弹性所引起的。

2.2初始缺陷作用下几何非线性稳定计算

对于高墩而言，混凝土浇筑的实际位置与理论位置难免存在一定的误差，而在日照温差的影响下，高墩也会发生一定的变形，因此，考虑这些因素的影响，高墩的初始缺陷是必然存在的。特征矢量屈曲模态可以认为是最接近于实际屈曲模态的预测值，因此本文采用以特征向量为依据的方法给结构施加初始缺陷[6]。本文考虑最大初始缺陷分别为0.1，0.3和0.5 m进行几何非线性稳定计算。计算结果如表5所示。

表5初始缺陷对几何非线性稳定的影响

Table 5 Influence of initial defects on geometrical nonlinear stability

初始缺陷大小/m00.10.30.5稳定安全系数15.1315.0214.8114.62稳定安全系数变化量/%0-0.70-2.10-3.40

从以上计算结果可以看出，考虑初始缺陷后，几何非线性稳定安全系数都发生不同程度的降低，但降低幅度不大，几何非线性的稳定安全系数仍较大，这座桥具有足够的几何非线性稳定安全系数。

2.3双重非线性稳定分析

本文的混凝土非线性本构关系采用国内外广泛采用的Hognestad公式，其具体表达式为：

(1)

图3　C55混凝土的本构关系Fig.3 Constitutive relation of C55 concrete

考虑双重非线性，利用Midas-FEA的空间实体单元对布林大桥在最大悬臂阶段的稳定性进行计算，迭代的方法采用收敛性较好的修正的牛顿拉普森法，以位移收敛标准进行计算。由于第1类稳定特征值屈曲荷载是结构第2类稳定临界荷载的上限[7]，可以作为双重非线性稳定分析的给定荷载，因此本节计算荷载取1.3节工况5的20倍。布林大桥在计算发散前的最大荷载加载系数为0.15，所以考虑双重非线性后，布林大桥的稳定安全系数为0.15×20=3。可见，考虑双重非线性后的稳定安全系数大于2.5，根据受压柱结构弹塑性稳定安全系数的规定[5]，满足规范要求。

从以上计算结果可以看出，布林大桥考虑材料非线性后，结构的稳定安全系数发生大幅度的下降，为考虑几何非线性结果的19.8%，为线弹性稳定安全系数的18.2%。因此，为得到结构真实的极限承载力，应考虑双重非线性，对第二类稳定问题进行计算分析。

3稳定性的影响参数分析

3.1混凝土强度等级对稳定性的影响

布林大桥高墩采用的是C55的混凝土，考虑C40，C50和C60不同标号的混凝土进行分析，讨论混凝土强度等级对稳定性的影响。计算结果如表6所示。

表6混凝土强度等级对稳定性的影响

Table 6 Influence of different strength grades of concrete on stability

混凝土强度等级C40C50C55C60第1类稳定安全系数15.1416.0716.5316.76稳定安全系数变化量/%-8.40-2.8001.40

从表6的计算结果可以看出，随着混凝土的强度等级的提高，稳定系数增大，但随着混凝土标号的增大，稳定安全系数的增幅趋缓，从C55变化到C60，稳定系数仅增大了1.4%，且高标号的混凝土还会带来现场浇注麻烦，结构的脆性增大等问题。因此，对高墩来说，从稳定性角度出发，当混凝土标号达到C50以上后，追求更高标号的混凝土是没有必要的。

3.2桥墩纵向尺寸对稳定性的影响

布林大桥最高墩纵向尺寸变坡率从墩顶到墩底采用200∶1，现采用不同的纵向变坡率讨论纵向尺寸对稳定性的影响，增加180∶1和250∶1共2种变坡率进行讨论分析,墩底的纵向尺寸从原来的5.276 m变为5.418 m和5.021 m。计算结果如表7所示。

表7　桥墩纵向尺寸对稳定性的影响

从表7可以看出，随着纵向尺寸的增大，桥墩的稳定系数也增大，纵向尺寸在原设计尺寸0.5 m左右范围内变化，其对稳定系数的影响也较有限，稳定系数的变化值在10%以内。

3.3双肢薄壁桥墩间距对稳定性的影响

连续刚构双肢薄壁墩间距的设计通常是从使得桥墩能够抵抗施工过程中可能出现的最大不平衡弯矩来考虑的[8]。为讨论双肢薄壁墩的间距设置在满足抗弯刚度要求的前提下对稳定性的影响，采取几种不同的桥墩间距进行稳定计算。布林大桥双肢薄壁墩的中心间距为12.5 m，现增加10.5，11.5和13.5 m这3种间距进行讨论计算。计算结果如表8所示。

表8双肢薄壁桥墩间距对稳定性的影响

Table 8 Influence of distance between two thin-walled piers on stability

双肢薄壁桥墩间距/m10.511.512.513.5第1类稳定安全系数16.0716.3016.5316.55稳定安全系数变化量/%-2.80-1.3000.10

从表8的计算结果可以看出，随着双肢薄壁墩间距的增大，稳定系数也增大。但各种间距下，稳定安全系数相差不大，因此，从稳定性及经济性角度考虑，双肢薄壁墩的间距在满足抗弯刚度要求的前提下，不宜取得过大。

3.4系梁设置对稳定性的影响

为分析系梁设置对稳定性的影响，设置不同的系梁个数对稳定性进行计算。

布林大桥的系梁的设置情况分为以下4种。

情况1)：未设置系梁；

情况2)：在距墩顶30 m的空心墩横隔板处设置1道系梁；

情况3)：在距墩顶58和62 m的空心墩横隔板处各设置1道系梁(布林大桥的实际情况)；

情况4)：在距墩顶30，58和62 m的空心墩横隔板处各设置1道系梁。

计算结果如表9所示。

表9　系梁设置对稳定性的影响

从表9计算结果可以看出，通过设置系梁都可以提高其稳定安全系数。在墩的中间设置1道系梁，对稳定安全系数的提高较大；但另一情况，即在靠近墩顶的地方设置1道系梁，其对稳定性影响较小，这说明系梁设置的位置，对稳定性有较大影响。与在墩的中间设置1道系梁相比，设置2道系梁并没有显著提高高墩的稳定安全系数，这说明当高墩的纵向刚度大到一定程度之后，设置更多的系梁是没有必要的。

3.5基础刚度对稳定性的影响

前面的计算都假定基础的刚度很大，忽略基础变形对稳定的影响，将墩底节点直接固结。为讨论基础刚度对稳定性的影响，下面对考虑桩-土作用的最大悬臂阶段的稳定性进行计算分析。本文采用分层文克尔弹簧模型[9-11]，将桩基础进行有限元离散，在单元节点上建立弹簧支撑，模拟桩周土对桩单元的约束。弹簧的刚度按《公路桥涵地基与基础设计规范》(JTG D63—2007)上的m法进行计算。

布林大桥最大悬臂阶段考虑桩土作用的有限元模型如图4所示。桩顶节点与承台底节点刚性连接，桩底节点固结，在桩的其他节点加上相应的水平弹簧约束。

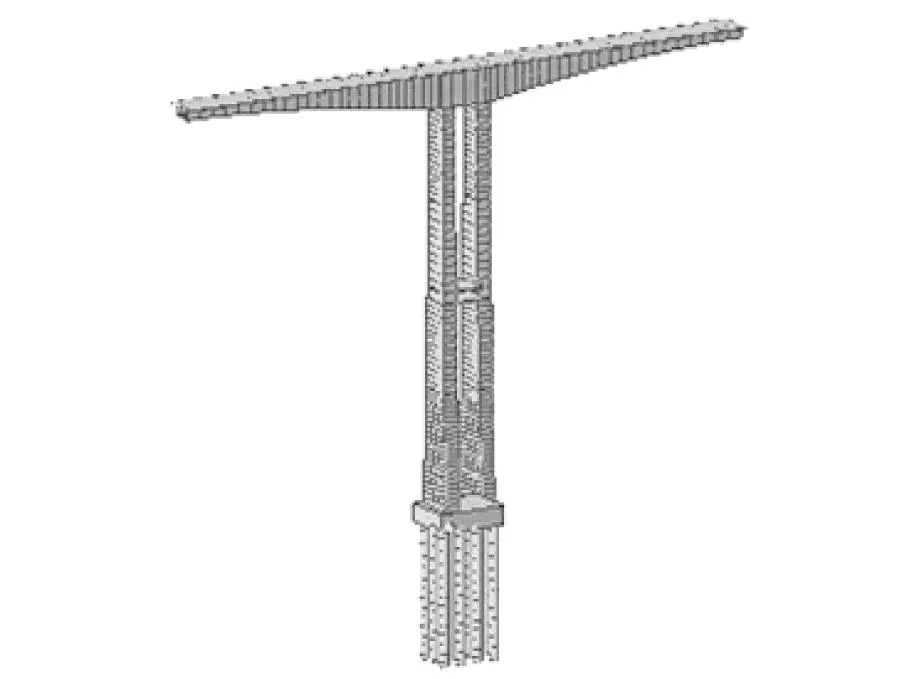
图4　考虑基础刚度的有限元模型Fig.4 Finite element model considering foundation stiffness

计算结果如表10所示。

表10　基础刚度对稳定性的影响

从表10的计算结果可以看出，基础刚度对稳定安全系数也有一定程度的影响，计入基础刚度后，线弹性稳定安全系数降低了12%。当进行初步设计时，可以不考虑基础刚度的影响，采用墩底固结的方式进行计算，快速得到初步的结果。而进行施工图设计时，应计入基础变形对结构的影响，精确计算连续刚构桥的内力和稳定性。

4结论

1)通过对布林大桥在最高墩阶段、最大悬臂阶段和成桥阶段的第1类线弹性稳定分析可知，最大悬臂阶段的稳定安全系数最小，应对其作重点分析。

2)与线弹性稳定相比，考虑几何非线性后，结构的稳定安全系数变化不大，说明桥的刚度较大，几何非线性对其稳定影响较小。同时，初始缺陷对桥梁的几何非线性稳定的影响也较小。

3)考虑材料非线性之后，结构的稳定安全系数发生了大幅度的降低。因此，为得到结构真实的极限承载力，仅进行结构的线弹性屈曲分析或几何非线性稳定分析是不够的，应进行双重非线性分析。

4)混凝土强度等级、桥墩的纵向尺寸、双肢薄壁墩的间距、系梁设置的个数及位置、基础刚度等对稳定性都有一定的影响。通过对结构稳定的影响因素进行分析探讨，得出了一些有益结论，可对高墩大跨连续刚构桥的设计和施工提供参考。

参考文献：

[1] 马保林.高墩大跨连续刚构桥[M].北京：人民交通出版社,2001.

MA Baolin. Long-span continuous rigid-frame bridge with high piers[M].Beijing:China Communication Press,2001.

[2] 陈骥.钢结构稳定理论与设计[M].北京：科学出版社,2011.

CHEN Ji.The theory and design of the structure stability of the steel[M].Beijing:Science Press, 2011.

[3] 郭梅.高墩大跨连续刚构桥稳定性分析[J].西安公路交通大学学报,1999,19(3):31-35.

GUO Mei. Stability analysis of long-span continuous rigid-frame bridge with high piers[J]. Journal of Xi’an Highway Communication University,1999, 19(3):31-35.

[4] 陈怀勇，汤兆新，陈胜利.高墩连续刚构桥稳定性分析[J].交通标准化，2010(6)：83-84.

CHEN Huaiyon, TANG Zhaoxin, CHEN Shengli. Stability analysis of high pier continuous rigid frame bridge[J].Communications Standardization, 2010(6)：83-84.

[5] JTG/T D65-01—2007,公路斜拉桥设计细则[S].

JTG/T D65-01—2007, Design specification for highway cable stayed bridge[S].

[6] 赖炼，白光耀.大跨度钢管砼拱桥考虑初始几何缺陷对极限承载力影响的计算机模拟[J].广西大学学报(自然科学版)，2006，31(增)：323-326.

LAI Lian, BAI Guangyao.The whole computer simulation process for initial geometry defects affect ultimate bearing capacity of concrete-filled steel tubular arch bridges[J]. Journal of Guangxi University(Natural Science Edition),2006，31(Suppl)：323-326.

[7] 黄海彬.高墩大跨连续刚构桥静力极限承载力及抗风性能研究[D].长沙：中南大学，2011.

HUANG Haibin. Research on static ultimate bearing capacity and wind-resistance performance of long-span continuous rigid-frame bridges with high piers[D].Changsha:Central South University,2011.

[8] 徐君兰，顾安邦.连续刚构桥主墩刚度合理性的探讨[J].公路交通科技，2005,22(2)：59-62.

XU Junlan, GU Anbang. Discussion of rationality of rigidity of continuous rigid-frame bridge[J]. Journal of Highway and Transportation Research and Development, 2005,22(2)：59-62.

[9] 刘钊，谭皓，文武松，等.连续刚构桥的群桩基础计算模型研究[J].桥梁建设，2005(5)：1-4.

LIU Zhao,TAN Hao,WEN Wusong.Research of calculation models for group pile foundation of continuous rigid-frame bridge[J].Bridge Construction, 2005(5)：1-4.

[10] 谌启发.虎跳门大桥桩基等效模拟计算[J].桥梁建设，2000(1)：69-71.

CHEN Qifa. Equivalent analog calculation for pile foundation of hutiaomen prestressed concrete continuous rigid-frame bridge[J].Bridge Construction, 2000(1)：69-71.

[11] 彭富强，李德建. 基于柔度系数求解桥梁桩基对桥墩约束刚度的有限元数值分析[J].铁道科学与工程学报，2012，9(2)：62-65.

PENG Fuqiang, LI Dejian. FEM numerical analysis of elastic bearing rigidity of pile foundation based on inverse deduction of flexibility coefficient [J]. Jounal of Railway Science and Engineering, 2012,9(2)：62-65.

(编辑阳丽霞)

Stability of long-span continuous rigid-frame bridge withhigh piers in mountain areas in different construction stage andrelevant parameter influence analysis

TANG Feng1，LI Dejian2

(1. Second Engineering Co.Ltd of CCCC Fourth Highway Engineering Co.Ltd, Beijing 101149,China;2.School of Civil Engineering, Central South University, Changsha 410075,China)

Abstract:On the background of a long-span continuous rigid-frame highway bridge with high piers in mountain areas, linear elastic stabilities were analyzed at the stages of completion of pier construction,the largest cantilever and completion of the whole bridge for finding the minimum stability safety coefficient , respectively. On this basis, nonlinear stability of the bridge was analyzed and the influences of nonlinear factors on stability were discussed. The influences of different parameters such as the concrete strength grade, longitudinal dimension of the pier, distance between the twin thin-walled piers, tie beam installation and foundation rigidity on stability were explored, and then some useful conclusions were drawn. The results can provide some references for the design and construction of long-span continuous rigid-frame bridge with high piers.

Key words:high pier; long-span; continuous rigid-frame bridge; stability; construction stage; nonlinearity

中图分类号：U443.22

文献标志码：A

文章编号：1672-7029(2016)03-0506-06

通讯作者：唐峰(1979-)，男，湖南邵阳人，高级工程师，从事桥梁工程施工与管理工作；E-mail：p30560632@qq.com

基金项目：湖南省交通科技计划项目(201022)

收稿日期：2015-10-28