空轨列车系统横向运动稳定性研究

李忠继，林红松，颜华，杨吉忠

(中铁二院工程集团有限责任公司，四川 成都 610031)



空轨列车系统横向运动稳定性研究

李忠继，林红松，颜华，杨吉忠

(中铁二院工程集团有限责任公司，四川 成都 610031)

摘要:采用多体动力学理论建立60自由度空轨列车系统动力学模型，模型考虑橡胶轮胎-轨道非线性相互作用特性，抗横摆减振器及空气弹簧等悬挂系统的非线性特性。利用等效线性化方法对非线性特征进行线性化形成单轨列车系统线性模型，通过系统根轨迹分析研究空轨列车系统稳定性。通过数值积分求解非线性模型的动态响应，基于此对空轨列车稳定性开展研究。结果显示：抗横摆减振器阻尼在10～1 000 kNs/m范围变动时，车体横摆阻尼比为0.6%～11%，为保证系统稳定，抗横摆减振器阻尼取值应大于200 kNs/m，以确保车体横向摆动能够快速收敛。轮轨游间对转向架的横向摆动和横向加速度有显著影响，特别是当游间较大时，转向架通过和驶出曲线时将会产生较为显著的横向冲击振动，其横向振动频率与车体横摆频率相同。在轨道设计中应尽量不设置较大的轮轨游间，在必须设置时应该确保抗横摆减振器具有足够阻尼，并对导向轮轮胎刚度进一步优化，以便减弱转向架和轨道梁间的冲击振动。

关键词：空轨列车；稳定性；抗横摆减振器；轮轨游间

空中轨道列车系统(简称空轨)是一种城市快捷轨道交通系统，轨道位于列车上方，由钢铁或水泥立柱支撑，转向架在轨道梁内行驶，列车通过悬挂系统吊挂在转向架下。作为一种新型中型运量的轨道交通系统，可以作为大型城市轨道交通系统的补充力量，也可以作为中小型城市的主干交通力量。空轨源于德国，在日本得到了进一步发展。Boehm等[1-2]综述了德国多特蒙德的空轨系统的组成、运行方式和主要特点；张静波等[3-8]综述了日本及其他国家悬挂式单轨列车系统的发展和应用情况；Meisinger等[9-10]建立了空轨车辆的4自由度模型，通过频响分析和数值仿真研究了车体在直线上受到周期性轨道激励下的动态响应。研究认为当激励频率高于系统固有频率时抗横摆阻尼采用无阻尼方式更优。但其未对车辆系统的稳定性和系统在低频激扰下的动态响应开展研究。由于空轨列车线路中存在很多小半径曲线，会对车辆系统横向方向产生较大激扰，且在实际中可能受到横风作用，因此有必要开展空轨列车系统的横向稳定性研究，这对车辆悬挂参数设计，轨道曲线设置及线路抗风设施设计都具有重要意义。本文采用多体动力学理论建立60自由度空轨列车系统动力学模型，模型考虑橡胶轮胎-轨道非线性相互作用特性，抗横摆减振器及空气弹簧等悬挂系统的非线性特性。利用等效线性化方法对非线性特征进行线性化形成单轨列车系统线性模型，通过系统根轨迹分析研究空轨列车系统稳定性。利用数值积分方法求解非线性模型的动态响应，基于此对空轨列车非线性稳定性开展研究。研究结果可为空轨系统的轨道和列车设计提供理论支撑和优化设计依据。

1研究方法和计算模型

1.1研究方法

空轨车辆的不稳定现象主要表现为列车在通过曲线、道岔或受到横风扰动等情况时车体横摆运动不能快速收敛，以及导向轮和导向轨间出现较大冲击振动等。悬挂式单轨车辆横摆稳定性研究的主要目的是研究车辆系统参数与系统稳定性的关系，确定系统的稳定域，分析系统在运行过程中的振动特征。常用的稳定性分析方法可以分为线性方法和非线性仿真方法。线性方法是将车辆系统模型线性化，通过求解系统的根轨迹来判断车辆系统的稳定性。非线性仿真方法可以计算系统在受到外部激扰时的动态响应，通过分析车辆系统运动衰减过程，确定系统振动的收敛速度和最大加速度等。在单轨列车系统中抗横摆减振器阻尼及导向轮和导向轨间隙对横向稳定性有重要影响，抗横摆阻尼特性决定了车体横摆运动的收敛速度，导向轮和导向轨间隙对轮轨冲击振动有显著影响。本文建立60自由度空轨列车系统动力学模型，通过线性和非线性方法研究系统的稳定性，及其与抗横摆阻尼和轮轨间隙的关系。

1.2计算模型

空轨车辆轨道系统由转向架、悬挂系统、车体和轨道梁组成，转向架包含驱动轮、导向轮、驱动电机、齿轮箱和构架。齿轮箱通过弹性节点和一系弹性橡胶块与构架连接，电机吊挂于构架两端，并通过传动轴与齿轮箱相连。驱动轮安装于齿轮箱两侧，与轨道梁走行面接触主要承担车辆系统的垂向力。导向轮水平安装于齿轮箱前端两侧，与轨道梁的导向面接触，起导向作用。导向轮和驱动轮均为实心橡胶轮胎。整个转向架在轨道梁内运行。构架下方伸出轨道梁，通过一可绕轨道方向摆动的铰连接摇枕，摇枕和构架之间装有抗横摆减振器。车体通过空簧吊挂与摇枕上，另外在车体和摇枕之间还安装了横向减振器、垂向减振器和牵引拉杆，图1为其结构简图。利用多体动力学计算软件UM建立车辆系统模型，如图2。模型将车辆系统考虑为多刚体系统，共包含25个刚体，60自由度。由于导向轮和驱动轮均为实心轮胎且在运行中侧倾角度较小，故采用Fiala轮胎模型来描述驱动轮、导向轮和轨道梁的相互作用关系。

表1　空轨列车系统自由度

图1　空轨车辆结构简图Fig.1 Simple figure of sky train

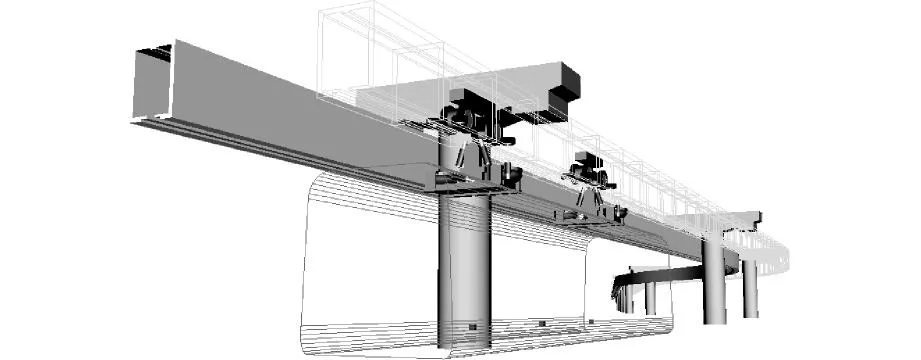
图2　空轨车辆动力学模型Fig.2 Dynamics model of sky train

1.3模型非线性特征

1.3.1轮轨非线性

本文研究的空轨车辆转向架装备有驱动轮和导向轮，驱动轮和导向轮均为实心橡胶轮。本文采用基于弹性地基梁理论的Fiala 轮胎模型来描述驱动轮和导向轮的力学行为。考虑轮胎和轨道出现间隙情况。轮胎和轨道间的法向力Fz为

(1)

其中：kz(·)为实心橡胶轮胎的法向非线性刚度函数；Δr为轮胎法向挠度；dz为实心橡胶轮胎的阻尼；VΔr为轮胎的垂向变形率。

轮胎纵向力为，

(2)

其中，

(3)

μ=μ0+(μ2-μ0)s

(4)

(5)

式中：sx为纵向蠕滑率；sy为纵向蠕滑率；cx为纵向蠕滑刚度；μx为静态摩擦因数;μ1为动态摩擦因数。

轮胎横向力为，

(6)

(7)

(8)

(9)

轮胎滚动阻力为

(10)

式中，rt为轮胎环形半径。

1.3.2抗横摆减振器非线性

抗横摆减振器的主要作用是抑制车体横摆，提高列车的运动稳定性和乘坐舒适性。抗横摆减振器的非线性特征是决定空轨列车系统稳定性的基本的参数。由于抗横摆减振器带有橡胶节点，因此抗蛇形减振器的动态行为可以用Maxwell模型(如图3)进行描述，阻尼力F可以表示为

(11)

图3　减振器的Maxwell模型Fig.3 Maxwell model of damper

2横摆稳定性线性分析

分析抗横摆减振器阻尼在10～1 000 kN·s/m范围内变动时，空轨车辆系统的模态频率～阻尼比轨迹图，如图4。可见车体的浮沉、横移、横摆等主要车体模态均在1.5 Hz以下，车辆系统横向主要模态阻尼比均高于5%。但当抗横摆减振器阻尼取10 kN·s/m时，车体横摆阻尼比小于5%，系统不稳定。随着抗横摆减振器阻尼增加，车体横摆阻尼比逐渐增加，当减振器阻尼取1 000 kN·s/m时，车体横摆模态阻尼比为11%左右。据线性分析结果可知：为保证车辆系统的稳定性，抗横摆减载减振器阻尼至少要应取到200 kN·s/m。否则车辆在运行过程中将会出现显著的低频横向摆动，且难于收敛，会使乘坐舒适性恶化。

图4　频率阻尼比轨迹Fig.4 Root locus of sky Train system

3横摆稳定性仿真分析

3.1横摆减振器的影响

为进一步分析不同横摆阻尼下，车辆系统的动态性能，计算抗横摆减振器阻尼取10，50，100，150和300 kN·s/m时，车辆以30 km/h的速度，通过半径50 m的曲线时的动态响应。图5为车体横向位移和加速度的时间历程，可见随着抗横摆阻尼的增加车体在通过曲线后低频晃动收敛速度会加快，当横摆减振器阻尼不足时，其通过曲线后的低频晃动非常显著，这与线性分析结果相吻合。车体通过曲线时的加速度主要成分为向心加速度。图6和图7为构架横向加速度及导向轮导向力。可见抗横摆阻尼对构架横向位移、横向加速度影响较小。但随着抗倾摆阻尼的增加，导向力会有所减小，其主要原因是车体横摆减弱。

(a)车体横向位移；(b)车体横向加速度图5　空轨车辆结构简图Fig.5 Displacement and acceleration of carbody

3.2轮轨游间的影响

计算轮轨单侧游间取 -2，0，2，4 m时车辆通过半径50 m曲线时的动态响应。图8～10分别为不同轮轨游间情况下车辆车体横向振动加速度、构架加速度和导向力的计算结果。可见轮轨游间对车体的横摆影响不显著，但其对转向架的横向摆动和横向加速度有较大影响，特别是当游间较大时，转向架通过和驶出曲线时将会产生明显的横向冲击振动，其横向振动频率与车体横摆频率相同。可推定当轮轨设置游间且横摆阻尼不足时转向架的这种横向振动也将难于收敛。因而在轨道设计中应尽量不设置较大的轮轨游间，在必须设置时应确保抗横摆减振器有足够的阻尼，且应对导向轮轮胎刚度进一步优化，以便减弱转向架和轨道梁间的冲击振动。

(a)构架横向位移；(b)构架横向加速度图6　构架横向位移和加速度Fig.6 Displacement and acceleration of frame

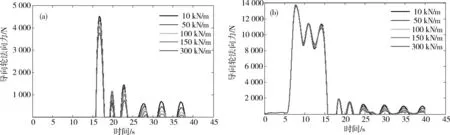
(a)一位转向架左前导向轮；(b)一位转向架右前导向轮图7　导向轮轮轨法向力Fig.7 Normal fore of steering wheel

(a)车体横向位移；(b)车体横向加速度图8　车体横向位移和加速度Fig.8 Displacement and acceleration of carbody

(a)车体横向位移；(b)车体横向加速度图9　构架横向位移和加速度Fig.9 Displacement and acceleration of frame

(a)一位转向架左前导向轮；(b)一位转向架右前导向轮图10　导向轮轮轨法向力Fig.10 Normal fore of steering wheel

4结论

1) 采用多体动力学理论建立60自由度空轨列车系统动力学模型，模型考虑橡胶轮胎-轨道非线性相互作用特性，抗横摆减振器及空气弹簧等悬挂系统的非线性特性。利用等效线性化方法和非线性仿真方法研究了系统稳定性;

2) 抗横摆减振器阻尼在10～1 000 kN·s/m范围变动时，车体横摆阻尼比为0.6%～11%，为保证系统稳定，抗横摆减振器阻尼取值应在大于200 kN·s/m，以确保车体横向摆动能够快速收敛;

3) 轨游间对对转向架的横向摆动和横向加速度有显著影响，特别是当游间较大时，转向架通过和驶出曲线时将会产生较为显著的横向冲击振动，其横向振动频率与车体横摆频率相同;

4) 在轨道设计中应尽量不设置较大的轮轨游间，在必须设置时应该确保抗横摆减振器具有足够阻尼，并对导向轮轮胎刚度进一步优化，以便减弱转向架和轨道梁间的冲击振动。

参考文献：

[1] Boehm E, Frisch H. The new operating system of the H-train in dortmund[J]. Verkehr und Technik,1994, 47(10): 465-470.

[2] Rahier H W, Scharf P. Sicherheitstechnische Prüfung der fahrerlosen kabinenbahn des flugha-fens duesseldorf[J]. Signal und Draht, 2002, 94(10):20-22.

[3] 张静波. 三菱悬挂型单轨铁路[J]. 世界轨道交通, 2005:13-13.

ZHANG Jingbo.MITSUBISHI suspended Monorail[J]. World Rail transit, 2005:13-13.

[4] 蒲全卫,陈喜红,陶功安,等.悬挂式独轨列车转向架[J]. 机车电传动, 2015(2):90-93.

PU Quanwei, CHENG Xihong, TAO Gongan, et al. Bogie of hanged-type monorail vehicle[J]. Electric Drive for Locomotives， 2015(2):90-93.

[5] 李芾,许文超,安琪.悬挂式单轨车的发展及其现状[J].机车电传动,2014:16-20.

LI Fu, XU Wencao, An Qi. Development and current status of suspended monorail vehicle[J]. 2014:16-20.

[6] Thwaite M. The george bennie railplane and hugh fraser airrail systems of transport[J]. Trans Newcomen Soc, 2005(75):37-84.

[7] Giesen U, Müller S. Die fahrzeuge des H-Bahn-Systems universität Dortmund[J]. Verkehr und Technik, 1983,36(10): 371-382.

[8] 齊藤勝.湘南モノレール江の島線の概要[J].新都市,1970,24(4):55-59.

Saito Katsu Shonan. Monorail line outline[J]. New Urban, 1970,24(4):55-59.

[9] Meisinger R. Dynamic analysis of the dortmund university campus sky train[J]. Schriftenreihe Georg Simon Ohm Fachhochschule Nürnberg, 2006:3-8.

[10] Meisinger R. Analysis of the lateral dynamics of a sky train with periodic track irregularities[C]// Proc of the Second International Conference on Dynamics, Vibration and Control, Beijing, China， 2006.

(编辑阳丽霞)

Study on the lateral motion stability of sky train system

LI Zhongji, LIN Hongsong, YAN Hua, YANG Jizhong

(China Railway Eryuan Engineering Group Co.LTD, Chengdu 610031, China)

Abstract:The dynamic model of sky train with 60 degrees of freedom was set up according to the theory of multiple body dynamics. The nonlinearity of tire track interaction, anti-swing damper, and air spring were considered in the model. The linearity model of sky train was formulated through making the nonlinearity model linear with the equivalent linearization method. The dynamic response of vehicle system was calculated to study the stability of sky train system. The results show that the swing damping ratio of vehicle is in the range of 0.6～11%, -when the damp of anti-swing damper is in the range of 10～1000kNs/m. The anti-swing damper damping value should be greater than 200kNs/m, in order to ensure that the lateral swing of the car can quickly converge for the stability of the system. The tire track clearance has a significant effect on the steering swing and lateral acceleration of bogie. Especially, when the clearance is large and the bogies go through or exits the curve sector, there will be more significant impact vibration. The impact frequency is the same as the one of carbody swing. Therefore, the overlarge wheel/rail clearance should not to be set. If the clearance is necessary, the anti-swing damper should have enough damping, and the tire stiffness of steering wheels need to be optimized for weakening the impact vibration between the bogie and the track beam.

Key words:sky train；stability；anti-swing damper；wheel / rail clearance

中图分类号：TP391

文献标志码：A

文章编号：1672-7029(2016)03-0564-06

通讯作者：李忠继(1983-)，男，河北赤城人，工程师，博士，从事车辆轨道动力学研究；E-mail：lizhongji4321@foxmail.com

收稿日期：2015-09-14