路基沉降的加权组合预测方法研究

许明明，徐彬，曾浩中

(1.宁波市公共交通客运管理局，浙江 宁波 315040；2.宁波市铁路建设指挥部，浙江 宁波 315040；3.同济大学 土木工程学院，上海 200092)



路基沉降的加权组合预测方法研究

许明明1，徐彬2，曾浩中3

(1.宁波市公共交通客运管理局，浙江 宁波 315040；2.宁波市铁路建设指挥部，浙江 宁波 315040；3.同济大学 土木工程学院，上海 200092)

摘要:基于路基沉降实测数据对沉降进行预测是一种常用的施工质量管理方法，然而单一预测模型往往可靠度不高。对此，通过系统分析当前常用的3种路基沉降预测模型，在此基础之上，对这3种方法的预测结果赋予不同的权值，进而加权求和得出最终沉降值，旨在减小预测结果的随机性，提高预测精度。研究结果表明：预测数据可靠度要优于单一模型，对比类似组合算法，在保证计算精度的基础上，计算效率也有了显著提升。

关键词：路基沉降；加权；组合预测

利用路基沉降的实测数据对路基沉降进行预测是一种实用的沉降趋势分析方法[1]，但是，无论采用哪种预测模型，都无法绝对准确反映路基沉降的真实情况，因为不同的模型关注的侧重点不同，所以计算结果会存在很大差异。所以一种常见的思想就是将2种或2种以上的算法组合起来[2-3]，以期减小预测结果的随机性，提高预测精度。对此，国内外学者作了大量研究。James等[4]以Logistics分布与遗传算法模型组合以预测路基短期沉降； Track[5]基于小波分析与神经网络法对轨道路基短期沉降作了预测；韩晋等[6]以神经网络修正灰色模型的残差；陈善雄等[7]以3点预测法改进指数曲线；魏春培[8]提出一种指数曲线与灰色预测的等权组合预测模型；李谆等[9]以三次样条插值处理GM(1，1)模型。但是以上算法或者是单一的对某种预测算法的改进，而并没有综合2种算法的优势[5,7,9]；或者以2种预测算法的嵌套实现预测，虽计算精度得以较大提高，但同时计算次数将呈几何级数倍增，从而导致计算效率大大下降，难以满足工程实际的需要[4,6,8]。因而一种思想便是采用加权组合的预测方法，将常用多种预测模型通过加权组合的方式结合起来[3]，以期减小误差的同时又不至于使计算量急剧增加。对此，本文首先用3种常用的路基沉降预测理论分别预测某一时间点的沉降，然后通过计算方差以一定的方法对这3个预测结果赋予不同的权值，进而减小预测的随机性，提高预测精度，既能综合各个常用路基沉降预测算法的优势，减小计算误差。同时，由于采用了加法结构将3种算法组合，不会使计算次数成倍增加，从而保证了计算效率。

1常用路基沉降预测算法综述

根据现有文献资料的分析总结[10]，当前路基沉降预测主要存在3种方法：曲线拟合法、灰色预测法和人工神经网络法。

1.1曲线拟合法[11]

该方法具有较为长久的应用历史，采用曲线拟合的方法对历史监测数据进行拟合，将曲线外部延伸以期求出后期的沉降量。曲线拟合的方法有很多，常用的有双曲线法与对数曲线法，2种方法计算效率与计算精度相差不大。此方法虽简便易行，但是容易存在较大的误差，尤其是当路基沉降的数据随时间波动较大时。本文采用双曲线法作为组合算法的一部分，具体计算公式为：

(1)

式中：yt为t时刻的路基沉降预测值；y0为初始路基沉降量，a和b为参数，由实测样本数据的最小二乘拟合计算。

1.2灰色预测法

灰色系统理论自诞生以来，在预测领域取得了重大的进展。灰色预测是将一组历史数据序列进行累加，再对累加序列采用一定方式进行逼近，将逼近模型作为预测模型从而实现预测[12]。在路基沉降预测中采用的是GM(1，1)模型。

此模型所需样本数据比较少，预测较为准确，精度较高，但是其精度受数据离散程度影响较为明显。GM(1，1)模型的解为：

(2)

1.3人工神经网络法[13]

人工神经网络法某个函数的自变量和因变量分别作为输入和输出，用高维非线性映射的方式表达函数关系而非数学表达式，非常适合处理非线性问题。因此通过建立沉降影响参数与沉降量之间的非线性关系，以实现预测。通常用以预测的是BP神经网络法，本文以文献[14]中的理论，对路基沉降预测问题建立模型，具体方法简要叙述如下。

采用网络结构为1×3×1的BP人工神经网络，并根据特定时间与对应沉降值形成训练样本，即隐含层选用3个神经元，1个时间输入对应1个沉降输出。网络的主要训练参数为：期望误差最小值为0.085，最大循环次数为30 000，设置学习速率为0.001，传递函数隐含层选用对数激活函数，输出层选为线性激活函数；当训练次数达到最大或者误差小于最小期望误差，训练停止，此时得出的预测值即为最终预测值。

人工神经网络法适合预测离散程程度较大的数据，但若想取得较为满意的预测精度，必须增大循环。次数，这会造成计算效率下降，采用这种算法往往计算效率和计算精度无法兼顾。本文之所以采用30 000次的循环次数，是因为要考虑一般PC的计算能力，但有时计算精度无法保障，故需组合以其他算法以提高预测精度。

2路基沉降的加权组合预测算法

由于单一预测算法精度容易受样本数据的影响，譬如当地质条件与气候条件均较好时，路基加载-沉降过程大致呈指数规律发展，此时无论用哪种预测算法都能取得较为满意的预测效果 (视样本数据多少选择具体算法)。但若气候环境变化较大，或者土体结构复杂，则沉降速率有时无规律可循，则单一预测算法可能会造成较大偏差。然而通常情况下，气候因素和地质因素均不理想，为保证预测结果的可靠性，考虑将这3种常用预测算法用加权的方式组合起来，具体方法如下。

2.1权值推导

记某一路基沉降预测问题的3种预测方法依次为f1，f2和f3(其中f1代表双曲线法，f2代表GM(1，1)模型，f3代表人工神经网络法)。对此，构造组合预测模型：

(3)

式中：ft代表t时刻的组合预测模型的预测值；fit代表第i种预测模型在t时刻的预测值；Ki代表第i种预测算法的权重，且有：

(4)

(5)

其中：

(6)

ei为第i种方法的均方差，且：

(7)

2.2预测步骤

根据以上分析，总结本文加权组合预测算法流程如图1所示。

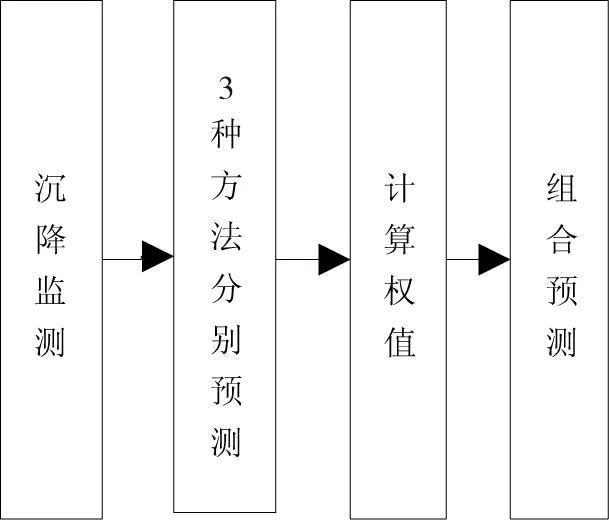
图1　预测算法流程Fig.1 Process of prediction method

具体步骤如下：

1)采取合适方法对路基沉降进行监测；

2)分别用3种常用预测方法对沉降数据进初步预测；

3)根据3组预测数据分别计算每种预测方法的权值；

4)根据权值以公式(3)对路基沉降进行最终预测。

3预测实例分析

3.1宁波绕城高速某处路基沉降预测

宁波绕城高速地处东南沿海地区，气候潮湿，降水量大，这种气候条件容易对高速公路路基土体产生影响，施工期间地基易产生沉降，为保证施工效率及控制工后沉降，有必要对施工路段进行沉降监测。现每相距100 m在路基断面中央埋设沉降盘，施工期间进行了为期0.5 a的沉降监测。现以监测时间30～170 d的15组沉降数据为例，取前10组数据为样本，用组合预测方法，预测出后5个监测时间点的数据。将实测值与预测值对比如图2所示。

由图2可见，该处路基沉降呈较为明显的沉降-固结变化规律，随着时间测推移，沉降速率趋于平缓，同时预测曲线大致反应了实际路基沉降的变化规律，证明采用本文算法可以达到较好的预测效果。将3种常用预测算法与类似组合预测方法与本文方法对比，结果如表1所示。

图2　宁波绕城高速某处沉降预测效果图Fig.2 Results of settlement prediction of a point in Ningbo beltway

由表1可见，由于本例沉降监测数据具有一定的规律性，离散程度较小，所以单一预测算法的预测精度均在5%以内，预测效果较好。采用加权组合预测法，能在此基础上进一步减小误差，使得相对误差均值仅为0.65%。对比文献[8]0.61%的预测精度相当接近，但计算时间仅为182 s,对比文献[8]效率大大提高。

3.2沪杭高速上海段某处路基沉降预测

沪杭高速上海段位于长江下游，属于典型的软土地区，这类地基特点便是强度低，压缩量较高，沉降量大。因此，为保证车辆通行安全，在通车之日起便对该高速公路进行了大量的沉降监测。以K168+540处的沉降数据为例，进行预测分析，在该处路基断面埋设沉降板与传感器，每隔一周记录一次沉降数据。现取7～98 d共14组监测数据，以前9组数据为预测样本，分别用3种方法对路基沉降进行预测，预测出后5个监测时间点的数据。将实测值与预测值对比如3.2沪杭高速上海段某处路基沉降预测沪杭高速上海段位于长江下游，属于典型的软土地区，这类地基特点便是强度低，压缩量较高，沉降量大。因此，为保证车辆通行安全，在通车之日起便对该高速公路进行了大量的沉降监测。以K168+540处的沉降数据为例，进行预测分析，在该处路基断面埋设沉降板与传感器，每隔一周记录一次沉降数据。现取7～98 d共14组监测数据，以前9组数据为预测样本，分别用3种方法对路基沉降进行预测，预测出后5个监测时间点的数据。将实测值与预测值对比如图3所示。由图3可见，由于该处地质条件的特殊性，路基沉降的变化并不具有明显的函数规律性，类似于这种数据，采用单一模型，则不可避免的产生较大误差[15],因此适合应用组合预测算法进行预测。图3中预测曲线仍能较好反映路基沉降的变化趋势。将3种常用预测算法与类似组合预测方法与本文方法对比，结果如表2所示。由表2可见，由于本例沉降监测数据离散程度较大，曲线拟合方法和灰色预测法预测效果均不理想。采用加权组合预测法，能够减小相对误差，使得相对误差均值缩减为2.86%。对比文献[8]中2.77%的预测精度接近，但计算时间仅为146 s,对比文献[8]效率大大提高。

图3　沪杭高速上海段某处沉降预测效果图Fig.3 Results of settlement prediction of a point in Shanghai-Hangzhou high-speed Shanghai segment

3.3宁波市兴宁路某处路基沉降预测

宁波市兴宁路位于城市中心地区，道路表面用沥青铺设，车流量大。由于夏季气温高，会造成沥青融化，进而引起路基沉降。为保障通车安全，故每年需要在高温时期期(6～9月期间)对该道路路基沉降进行监测(每隔5 d，采用单点沉降计测量)。现取2014年7～8月60 d期间12组监测数据，，以前7组数据为预测样本，分别用3种方法对路基沉降进行预测，预测出后5个监测时间点的数据。将实测值与预测值对比如图4所示。

由图4可见，由于气温条件变化不定，路基沉降的变化并不具有明显的函数规律性，采用单一模型，则会产生较大误差[15]，因此适合应用组合预测算法进行预测。图4中预测曲线仍能较好反映路基沉降的变化趋势。将三种常用预测算法与类似组合预测方法与本文方法对比，结果如表3所示。

由表3可见，同样，由于本例沉降监测数据离散程度较大，曲线拟合方法和灰色预测法预测效果均不理想。采用加权组合预测法，能够减小相对误差，使得相对误差均值缩减为0.88%。对比文献[8]中0.82%的预测精度接近，但计算效率大大提高。

表1　宁波绕城高速某处路基沉降不同方法预测效果对比

表2沪杭高速上海段某处路基沉降不同方法预测效果对比

Table 2 Prediction results by different comparison for subgrade settlement of a point in Shanghai-Hangzhou expressway Shanghai segment

预测方法时间/d 双曲线法 灰色预测法 人工神经网络 本文方法 文献[8]方法 预测值/mm误差/%预测值/mm误差/%预测值/mm误差/%预测值/mm误差/%预测值/mm误差/%实测沉降/mm70116.532.38134.1212.36112.235.98116.282.59115.862.94119.3777117.023.39137.6313.63116.254.02117.143.29122.210.90121.1284118.032.56136.0312.30129.036.52125.213.37129.036.52121.1391118.249.84136.764.29130.280.66135.973.68130.780.27131.1498118.7613.48137.130.10136.730.39139.191.40132.913.18137.27误差均值/%-6.33-8.54-3.11-2.86-2.77-计算耗时/s0.250.871451464493-

表3　兴宁路某处基沉降不同方法预测效果对比

图4　兴宁路某处沉降预测效果图Fig.4 Results of settlement prediction of a point in Xingning road

4结论

1)详细分析了常用路基沉降预测方法的优势与局限性，对合理选择沉降预测方法提供了一定的参考。

2)提出了一种加权组合的预测方法，给出了权值计算的公式，对减小计算结果的随机性，提高预测精度具有一定作用。并且这种加权组合的思想亦可广泛应用于类似预测问题中。

参考文献：

[1] 曾鼎文，吴浩中.优化的非等时距灰色模型在湖南高速公路基沉降预测中的应用[J].公路工程, 2013,38(4): 269-272.

ZENG Dingwen, WU Haozhong. Application of optimization unequal time-interval gray model in forecast of subsidence of embankment settlement of expressway[J]. Highway Engineering, 2013，38(4): 269-272.

[2] 梁承翔，尹建军.垄茶高速公路土石混填路基沉降分析[J].公路工程,2014,39(5): 270-273.

LIANG Chengxiang, YIN Jianjun. Study on settlement character of stone embankment in Longcha highway[J]. Highway Engineering, 2014,39(5): 270-273.

[3] 付宏渊.路基沉降计算影响因素及预测方法研究[J].中外公路，2007,27(5)：53-55.

FU Hongyuan. Research on the calculation influencing factors and prediction method for subgrade settlement[J].Journal of China & Foreign Highway，2007,27(5)：53-55.

[4] James, George E. Results of subgrade[J]. Practice Periodical on Structural Design and Construction,1997,2(3):105-117.

[5] Track B. Expressway subgrade settlement prediction[J]. Journal of Protective Coatings and Linings,2007:24(7):18-28.

[6] 韩晋，杨岳，陈峰，等.基于非等时距加权灰色模型与神经网络的轨道不平顺预测[J].铁道学报，2014,36(1):81-87.

HAN Jin，YANG Yue，CHEN Feng，et al. Prediction of track Irregularity based on non-equal interval weighted grey model and neural network[J]. Journal of China Railway Society,2014,36(1):81-87.

[7] 陈善雄，王星运，许锡昌，等.路基沉降预测的三点修正法[J].岩土力学，2011，32(11)：3355-3360.

CHEN Shanxiong, WANG Xingyun, XU Xichang，et al.Three-point modified exponential curve method for predicting subgrade settlements[J]. Rock and Soil Mechanics , 2011，32(11)：3355-3360.

[8] 魏春培.高速公路路基沉降的组合预测研究[J].科技资讯，2012，12(14)：60-61.

WEI Chunpei. Highway subgrade settlement of combination Forecasting[J]. Science and Technology Information, 2012，12(14)：60-61.

[9] 李谆，金鼎沸.基于三次样条插值和GM(1，1)模型的路基沉降预测[J].公路工程，2015，40(2)：221-226.

LI Zhun, JIN Dingfei. Prediction of highway sudgrade based on cubic spline interpolation and GM(1,1) model[J]. Highway Engineering, 2015，40(2)：:221-226.

[10] 许嵬.常用路基沉降方法分析对比[J].湖南交通科技，2013，39(3)：36-39.

XU Wei. Methods commonly used contrast subgrade settlement[J]. Hunan Traffic Science and Technology, 2013，39(3):36-39.

[11] 金亮星，李小刚.泊松曲线法在填海造地道路软基沉降预测中的应用[J].铁道科学与工程学报，2013，10(5)：52-56.

JIN Liangxing, LI Xiaogang. Application of posson curve method in the prediction of road soft foundation settlement for land reclamation[J]. Journal of Railway Science and Engineering. 2013，10(5)：52-56.

[12] 刘思峰，谢乃明.灰色系统理论及其应用[M].北京：科学出版社，2011.

LIU Sifeng, XIE Naiming. Grey system theory and its applications[M]. Beijing：Science Press, 2011.

[13] 韩力群.人工神经网络教程[M].北京：北京邮电大学出版社，2006.

HAN Liqun. Artificial neural networks tutorial [M].Beijing: Beijing University of Posts and Telecommunications Press, 2006.

[14] 陈亭.综合神经网络法及双曲线拟合法预测软基沉降[J].路基工程，2008(5)：151-153.

CHEN Ting. Integrated neural network and hyperbolic fitting soft ground settlement prediction [J]. Subgrade, 2008(5)：151-153.

[15] 叶观宝，司明强，赵建忠,等.高速公路路基沉降预测的新方法[J].同济大学学报，2003, 31(5)：540-545.

YE Guanbao, SI Mingqiang, ZHAO Jianzhong, et al. New prediction method on final settlement on expressway[J]. Journal of Tongji University, 2003, 31(5)：540-545.

(编辑蒋学东)

Research on weighted combination prediction methodfor subgrade settlement

XU Mingming1, XU Bin2, ZENG Haozhong3

(1. Ningbo Public Tromgport Administration Stration, Ningbo 315040 ,China;2. Ningbo Railway Construction Headquarters， Ningbo 315040, China;3. School of Civil Engineering , Tongji University, Shanghai 200092, China)

Abstract：To predict the subgrade settlement basing on the original settlement data is a common method for construction quality management. However, the reliability of a single prediction models are often not high. Therefore, this paper analyzed the current three common subgrade settlement prediction model systematicallyand given different weights for the results of these three methods. The final settlement prediction value can be achieved. It is aimed to improve forecast accuracy. In the prediction test, the results show that this method is superior to a single model. Compared with similar combination algorithm, the accuracy can be ensured, but computational efficiency has been significantly improved.

Key words：subgrade settlement; weighed; combined prediction

中图分类号：U416

文献标志码：A

文章编号：1672-7029(2016)03-0463-06

通讯作者：曾浩中(1965-)，男，江苏泰安人，教授，从事岩土力学研究；E-mail:zhz196562@163.com

基金项目：国家自然科学基金资助项目(51078151)；交通部应用基础研究面上资助项目(2011319495090)

收稿日期：2015-08-02