高速列车的节能操纵策略研究

宋文婷，谭觅，蔡文川，范礼乾

(1.北京交通大学 智能系统与再生能源研究中心，北京 100044；2.重庆大学 自动化学院，重庆 400044；3.北京交通大学 轨道交通安全及控制国家重点实验室，北京 100044)



高速列车的节能操纵策略研究

宋文婷1，谭觅2，蔡文川1，范礼乾3

(1.北京交通大学 智能系统与再生能源研究中心，北京 100044；2.重庆大学 自动化学院，重庆 400044；3.北京交通大学 轨道交通安全及控制国家重点实验室，北京 100044)

摘要:以高速列车的节能运行为研究目标，充分考虑列车的牵引特性和运行线路条件，构建定时约束下的列车操纵模型，进而提出针对优化运行速度曲线的节能操纵策略。首先引入组合优化技术，通过遗传算法为子区间搜索最优的速度码组合序列，将模型求解转换为最优化问题，获得列车节能运行的速度操纵范围。然后在此基础上，充分利用线路坡度，提出坡道加速度一次变更原则，并结合列车牵引、巡航、惰性和制动的操纵模式，最后获得能耗最小的运行速度曲线，指导高速列车下一站间的运行。通过京沪线上的站间实例仿真，验证了节能操纵策略的有效性。

关键词：高速列车；节能策略；组合优化技术；遗传算法；坡度

由于高速列车的快速性、舒适性和安全性，高速铁路得到了快速发展，并在交通运输中扮演越来越重要的角色[1]。然而随着高速列车运量的增加和运行距离的延长，其能源消耗总量十分巨大。因此国内外许多学者致力于研究高速列车运行的节能优化问题，期望获得更好的控制策略，使列车在运行过程中能耗最小。现代优化控制理论最早用于此方面的研究，Asnis等[2]以加速度和牵引力作为输入变量，为列车的节能控制寻求最佳解决方案。Howlett等[3-4]建立了适当的列车运行优化模型，并以极小值原理和KuhnTuck方程分别研究了在输入变量为连续和离散2种情况下，列车的最优控制问题。而事实上由于列车自身的结构，连续控制变量并不能始终与实际操作保持一致。随着智能算法的不断发展和成熟，以离散变量为控制输入的研究方式受到更多的关注，模糊控制、预测理论和启发式算法等相继被采用，对应的离散输入控制变量也更符合列车的实际情况。Shoji等[5-6]最早进行了相关的研究，他们将模糊控制和预测理论运用到列车控制，通过总结实际的列车操纵经验，构建了预测模糊列车控制系统。Kawakami[7]为日本的新干线设计了一种动态的牵引节能策略，也采用了预测控制理论。随着我国高铁建设的发展，越来越多的学者开始从事高速列车节能运行的研究[8-12]。并且对于能耗和运行时间的相互关系也有学者进行了探索，以此来决定高速列车的经济运行模式[13]。本文以高速列车的牵引计算为基础，充分考虑列车运行中的各种因素，采用速度编码及组合优化技术，通过遗传算法搜索获得基础节能速度曲线，再利用线路坡度优势来调整列车操纵模式，以降低实际运行能耗，达到高速列车节能运行的目的。

1模型建立

1.1运动方程描述及受力分析

列车在运行过程中需要施加牵引力来产生加速度和克服来源于列车速度和线路条件的阻力，并以相对恒定的速度来维持其运行舒适性和能耗稳定。在长距离的高铁线路运行中，将列车视为一个单粒子个体，其运动过程描述如下：

(1)

(2)

式中：F和B分别是列车运行速度为v时的牵引力和制动力；f0，fg，fr和fs分别是列车运行中的基本阻力，坡度阻力，曲线阻力和隧道阻力；x是列车当前位置；M表示列车的重量，值随列车负载变化。

影响基本阻力的主要因素是列车的运行速度，由Dvis方程给定：

f0=a1+a2v+a3v2

(3)

式中：a1为滚动阻力；一次项a2v是列车的机械阻力；二次项a3v2是列车所受的空气阻力。

附加阻力来源于运行的线路条件，分别表示如下：

(4)

式中：g是重力加速度；hk为运行线路上第k个坡度变化的高度；sk为此线路坡度长度。在上坡时，fg为正值，阻碍列车运行，在下坡时，fg为负值，具有推动列车运行的效果；R为线路曲线半径；LS为隧道的长度。

1.2制动点确定

在建立优化控制模型前先定义区间线路上一个重要位置xb——进站制动点。在遗传算法搜索速度码阶段，列车除了进站采取必要制动外，其余路线上列车运行均采用牵引、巡航和惰行的操纵模式以达到节能目的。本文中我们根据列车停车制动经验给定一个制动减速度ab，并从运行终点反推制动速度轨迹，获得制动距离sb，如图1所示。

图1　停车制动曲线Fig.1 Brake curve

设定车列车载制动点时的运行速度为vb，则由牛顿公式可以得到制动距离sb

(5)

因此，可以计算推出制动点的位置为xb=s-sb，s为两站间的距离。

1.3节能模型建立

根据节能运行目标，高速列车装有再生制动设备，使列车在制动时会反馈能量到电网或车载储能设备，因此在建立能量模型时牵引消耗能量和再生制动获得能量要分步进行计算。根据列车当前的运行位置xi，当xi∈(x0,xb)时，列车处于耗能阶段，此阶段的操纵模式为牵引、巡航和惰行，能耗模型表示如下：

(6)

式中：x0为列车在出发站的起始位置；η为列车牵引效率，与列车运行速度有关[14]。

当xi∈(xb,xs)时，列车处于制动反馈能量阶段，通过制动操纵模式达到进站精准停车，车载再生制动设备可将列车制动产生的动能转化为电能，则此阶段再生制动反馈的能量为：

(7)

式中：Xs是列车进站的运行终点位置;λ是列车制动效率，与列车运行速度有关[11]。

综上所述，列车在2个连续站间运行的总能耗为：

E=E1-E2

(8)

将列车所在位置作为自变量，则其变化范围为(0,xs)，对应的列车运行时间为：

(9)

式中：v(x)和t(x)分别为列车在x处的运行速度和累计运行时间。同时，为保证安全准时运行，列车还要满足各项约束条件。因此建立的节能模型如下：

minE=E1-E2

s.tv(x0)=v(xs)=0,v(xi)< vlimxi

T-Δt≤t(xs)≤T+Δt

(10)

式中：t(xs)是列车总运行时间；Δt是允许时间误差；v(x0)和v(xs)是列车起点和终点速度；v(xi)为列车在线路上第im的运行速度；vlimxi为相应的限速。

2策略分析

从2个层面对高速列车进行节能优化操纵，一是确定其节能运行的速度范围，这部分采用组合优化技术和遗传算法，以速度码的形式，为列车搜索出一条基础节能速度曲线，为了能更充分地利用线路坡度具有的节能优势，因此将此曲线平稳运行阶段的速度增减一定范围后，得到速度的区间为列车实际运行的节能速度范围；二是在节能速度范围内，根据线路坡度进行列车操纵模式的转换，使列车运行达到进一步的节能效果，同时满足各项约束条件。

2.1基础节能速度

2.1.1过程概述

为确定适合的节能运行速度范围，首先确定基于速度码的列车运行基础节能速度，在线路离散过程中，文献[15]提出一种等分线路长度的离散方法，但是由于高速列车运行距离较长以及其线路上频繁的坡度变化，本文将线路长度按坡道离散化，建立子区间，并通过遗传算法为每个子区间搜索一个适合的目标速度。具体概括如下：假设制动点位于第n个坡道，则制动点前的每一个等坡度值的坡道距离为一个子区间，剩余线路整体为一个子区间，则此线路区间集合为(s1,s2,s3，……，sn-1,sn)。速度按等速度差原则离散化为一组目标速度，即为速度码，集合为(v1,v2,v3，……，vm-1,vm)，其中v1为列车空转速度，vm为线路上允许的列车最大速度。组合优化技术就是对子区间和区间速度码进行组合，获得一组最优的速度码组合序列，使列车沿此速度码序列运行产生一条当前能耗最小的速度运行曲线。图2是一个最优速度码序列下对应的速度轨迹示意图。

图2　列车基础指导速度曲线示意图Fig.2 Biagram of the train guidance speed curve

4.发展落后的农村保险业。农业保险的特点是回报率低、赔付率高。在中国保险业商业化经营之后，由于保险公司的生存需求，需要提高保险业务的经济效益，因此农业保险业务量逐渐下滑，发展状态日渐萎缩。在一定程度上，滞后的农业保险致使金融机构对农业及农村企业的风险评估相对的提高，这一原因成为“惜贷”的重要原因之一。农村保险业组织发展滞后性不仅恶化了农村金融原本的供给紧张程度，而且严重阻碍了发展农业现代化和社会主义新农村建设的步伐。

2.1.2遗传算法寻优

遗传算法通过全局并行搜索方式来获得种群中最优的个体，在本文中则是搜索出一组对应能耗最小的速度码序列，这里对列车速度码序列R采用实数编码的方式来表示各种组合情况。具体过程描述如下。

1)种群初始化

编码：根据子区间的划分数目，在染色体上编码n个基因，每个基因的取值范围为实数1～m，对应m级速度码。根据高速列车的牵引特性，将初始子区间和最后制动区间的目标速度设为v1，即在染色体中编码为1，使列车在加速之后能够以恒功率运行，进站做到精准停车，其余子区间的速度码随机产生。

种群产生：根据以上编码机制的定义，随机产生一定数目的染色体形成初始种群P。

2)运行性能指标与适应度

针对生成的每一个速度码序列，计算出列车沿此速度码运行的能耗，并以限速和精准停车等为约束条件，去除无效的速度码序列。在实际中以时间误差允许范围内能耗最小为目标，将性能指标函数定义为

(11)

式中：E为列车在运行区间的能耗；β为时间比重系数。则个体适应度f可以表示为

(12)

式中：A为设定的调整系数。

3)判断是否收敛

当算法达到最大迭代次数，输出结果，否则继续进行下面的操作。

4)遗传操作

选择：以轮赌法选择出相应数目个体，并采用最佳保留选择的操作方式，这样能保证遗传算法终止时得到的最后结果是历代中出现过的适应度最高的个体。

交叉：设定一个交叉概率Pc，随机选出父辈中交叉的个体并进行两两配对。采用单点交叉方式，得到两条新的染色体：

R1=(R11,R12…R1j,R2j+1…R2n-1,R2n)

R2=(R21,R22…R2j,R1j+1…R1n-1,R1n)

(13)

变异：同样设定一个变异概率Pm，随机确定发生变异的染色体，采用单点变异的方式随机确定一个变异的基因，在满足约束的条件下修改该点值为任意值。

5)更新

种群中个体完成以上操作，得到新一代个体，返回步骤2)。

2.2运行推荐速度

通过基础节能速度确定了列车节能运行的速度范围，主要有2方面优势：一是列车在一个比较节能的速度上下限约束内，可以充分利用线路坡度，以惰行操纵模式再次降低运行能耗。二是列车在相对比较小速度波动范围内运行，避免了因较大运行速度调整给乘客带来的不舒适性。在这层速度优化过程，中间平稳阶段可能存在少量部分制动的操纵模式，制动反馈能量可忽略不计。

2.2.1坡道分类和加速度一次变更原则

本文中，我们根据线路坡度对高速列车运行产生的作用，对线路坡道进行分类，因此可以分为以下3种类型：阻力坡道: fg>0，坡道坡度具有阻碍列车运行的作用，可以通过牵引使列车保持匀速或加速运动状态。推力坡道：fg<0，坡道坡度具有推动列车运行的作用，在此坡道上应尽可能的惰行，以充分利用坡道势能，从节能的角度考虑是有很大优势的;平道：fg=0，适用于列车加速为后面惰行做准备。

根据列车司机操作经验，坡度是改变列车运行状态的主要参考依据，并且不同坡度上的实际操纵是研究节能问题的关键，为给出具体的节能操纵模式，提出坡道加速度一次变更原则。本文中，已知坡道起始处的速度，坡道一次加速度变更原则即是列车在坡道起始处根据此区间的坡道类型进行恒定的加速或减速运动，达到速度限制后列车匀速运行至坡道终点，或者坡道距离较短时，列车一直保持某个加速度运动状态，即一个坡道上列车加速度变化最多为一次。这样不仅降低了能耗计算的复杂度，同时也有利于节能策略的实施。

2.2.2节能操纵

高速列车在两站间运行共分为3个阶段，初始加速阶段、平稳运行阶段和停车制动阶段。列车在初始加速阶段和停车制动阶段基本按照基础节能速度曲线运行，以保证列车以较低能耗加速到平稳运行速度，并在进站期间完成精确停车。中间平稳运行阶段是列车主要的运行阶段，占用大部分运行时间，因而此阶段的节能操纵是列车节能优化的重点。根据坡道的节能操纵策略，列车速度调整方法以图3为例。

图3　列车速度调整曲线Fig.3 Adjustment train speed curve

在节能运行速度范围内，列车以坡道类型作为操纵模式的选择依据。列车在平道OA上以恒定加速度运行，并且由于此段距离较短，列车低于上限速度条件下可一直加速到坡道终点。若平道距离较长，列车提前达到运行速度上限，则在此时列车的操纵模式转换为巡航。在上坡坡道AB上，对列车施加部分牵引力使之保持匀速运动状态，为下坡惰行做准备。在下坡坡道BC上，列车充分利用坡道坡度优势，采用惰行模式达到节能操纵的目的，但是由于此坡道距离较长，列车在坡道中间达到运行速度下限，因此转换为巡航模式运行到坡道终点。若此坡道坡度较陡，也可能存在采用惰行模式使列车速度增加，这种情况下列车速度达到运行速度上限时准换为巡航模式。在中间运行阶段的每个加速坡道上，通过搜索每个合理的加速度值，可以达到节能性和准时性的目标。

3实例仿真

本文中，以京沪线上的枣庄站到徐州站间的线路为研究实例，此段路线全长65 km，运行时间为18 min，允许时间误差为30 s，区间限速情况为200到350 km/h。高速列车为动力分散性动车组CHR3，以4动4拖的机构组成，车辆模型数据见表1。

表1　CHR3列车参数

在遗传算法中，设置种群的规模为200，交叉和变异的概率分别取0.8和0.008，算法迭代次数为300次。图4为运用遗传算法优化得到的速度码及列车按此速度码运行得到的基础节能速度曲线。这条速度曲线保证了列车运行时间，并且通过合理安排速度达到了一定的节能效果，但是坡道节能优势还没有充分利用。在基础节能速度基础上，通过下坡惰行节能，进一步得到列车运行的推荐速度，图5为最终的仿真结果，包括列车限速和实际运行速度，列车在中间稳定运行阶段根据坡道进行速度调整，在制动阶段先通过部分制动使列车速度由平稳阶段降低到最终制动前所需的速度。列车的运行总能耗为1 788.6 kWh，运行时间为1 063 s，可以满足时间的要求。图6是牵引功率和线路坡度的对照图，可以清楚的看到列车在中间运行阶段，通过下坡采用惰行的操纵模式，不消耗能量，从而降低了列车整体运行能耗。在最后停车进站过程，由于采用再生制动方式，牵引功率变为负，表示为再生制动反馈的能量。

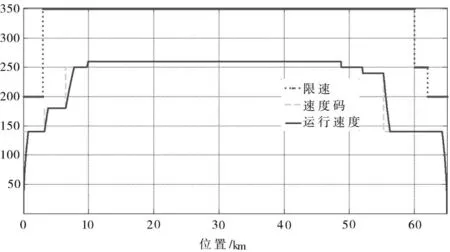
图4　列车基础节能速度曲线Fig.4 Fundamental energy-saving speed curve

图5　节能策略下的列车速度曲线Fig.5 Train speed curve with energy-saving strategy

图6　坡度和牵引功率变化情况Fig.6 Varieties of gradient and traction power

为了说明本文节能操纵策略的有效性，将列车正常行驶的运行能耗作为对比，这里列车以最大牵引力加速到一个适当速度，保持匀速运行，最后采用制动模式减速。图6是列车以相等于节能策略中的运行时间获得的速度轨迹，总运行能耗为2 045.7 kWh。图7为此运行过程中牵引功率随坡度信息变化情况，可以看到在不采用节能优化策略时，整个运行过程中牵引力都存在，列车进行着耗能。虽然2种运行方式下的平均速度相同，但能耗差别很大。本文提出的操纵策略能在合理的速度范围内充分利用坡度节能12.6%，因此证明了此操纵策略的有效性。

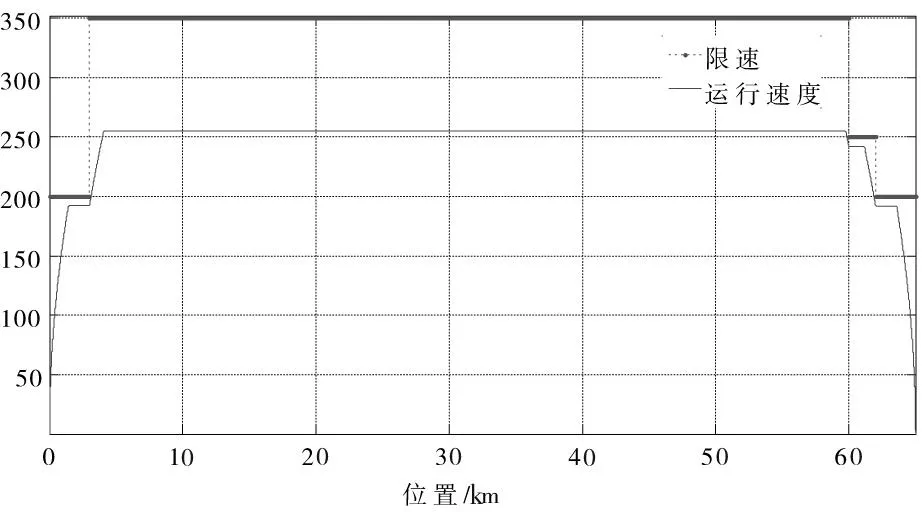
图7　无节能策略的列车速度曲线Fig.7 Train speed curve without energy-saving strategy

图8　坡度和牵引功率变化情况Fig.8 Variation of the gradient and traction power

4结论

1)以高速列车的节能运行为优化目标，建立精准可靠的站间列车操纵模型，考虑高速列车的再生制动及运行线路条件，使列车运行更加符合实际条件。

2)从2个层面提出节能操纵策略，引入遗传算法和组合优化技术为列车搜索出一条基础节能速度曲线，进而给出列车节能运行的速度范围，这种方式避免了一些微分方程和非线性问题的数学计算，同时以搜索速度码的方式获得运行轨迹不需要设置过多的决定参数，简化了解决方案的复杂度。在一个合理的速度约束范围内，充分利用坡道坡度惰行，进一步降低运行能耗，提高了计算的速度，最终获得一条能耗最小的推荐速度曲线。

3)通过实例仿真验证，本文策略能满足限速及时间约束，实现列车定点、精准停车，并且达到节能运行的最终目的，因此本文操纵策略是可行且有效的。

参考文献：

[1] 陈涛. 高速列车运行能耗测算方法及其影响因素量化分析[D]. 北京：北京交通大学，2011: 4.

Chen Tao. Traction energy consumption measuring methods study and quantification analysis on energy impact factors of high-speed train [D]. Beijing: Beijing Jiaotong University, 2011: 4.

[2] Asinis I, Dmitruk A, Osmolovsk II N. Solution of the problem of the energetically optimal-control of the motion of a train by the maximum principle [J]. USSR Computational Mathematics and Mathematical Physics, 1985, 25(6): 37-44.

[3] Howlett P, Pudney P. Energy-efficient train control [M]. New York: Springer Press,1995:79-82.

[4] Howlett P. The optimal control of a train [J]. Annals of Operations Research, 2000, 98(1):65-87.

[5] Shoji M, Yasunobu S, Hirokasu I. Predictive fuzzy control and its application to automatic train operation systems[J]. Analysis of Fuzzy Inference, 1987, 5(12): 59-72.

[6] Oshima H, Yasunodu S, Sekino S. Automatic train operation system based on predictive fuzzy control [J]. International Workshop on Artifitial Intelligence for Industrial Applications, 1998, 76(5): 485-489.

[7] Kawakami T. Integration of heterogeneous systems [C] // Proceedings of the Fourth International Symposium on Autonomous Decentralized Systems, 1993: 316-322.

[8] 王鹏玲，林轩，李跃宗，等. 自适应遗传算法在列车节能优化中的应用[J]. 计算机仿真，2012，29(11)：350-354.

WANG Pengling, LIN Xuan, LI Yuezong, et al. Energy saving train operation optimization with adaptive genetic algorithm [J], Computer Simulation, 2012, 29(11): 350-354.

[9] 刘建强，魏远乐，胡辉. 高速列车节能运行优化控制方法研究[J]. 铁道学报，2014，36(10)：7-12.

LIU Jianqiang, WEI Yuanle, HU Hui. Research on optimization control method of energy‐saving peration of high-speed trains [J]. Journal of the China Railway Society, 2014, 36(10)：7-12.

[10] SU Ruidan, GU Qianrong, WEN Tao. Optimization of high-speed train control strategy for traction energy saving using an improved genetic algorithm [J]. Journal of Applied Mathematics, 2014, 45(8): 45-51.

[11] LI Liang, DONG Wei, JI Yindong, et al, TONG Lang. Minimal-energy driving strategy for high-speed electric train with hybrid system model [J]. IEEE Transactions on Intelligent Transportation Systerms, 2013, 14(4): 1642-1653.

[12] SUN Shiyao, LI Yang, XU Huaiyu. Energy consumption optimization for high-speed railway based on particle swarm algorithm [C] // Proceedings of International Conference on Systems and Informatics, 2012: 34-39.

[13] Hwang H S. Control strategy for optimal compromise between trip time and energy consumption in a high-speed railway [J]. IEEE Transactions on Systems, Man, and Cybernetics A: Systems and Humans, 1998, 28(6): 791-802.

[14] Williamson S, Lukic M, Aliemadi. Comprehensive drive train efficiency analysis of hybrid electric and fuel cell vehicles based on motor-controller efficiency modeling [J]. IEEE Transactions on Power Electronics, 2006, 21(3): 730-740.

[15] KE B R, LIN C L, YANG C C. Optimisation of train energy-efficient operation for mass rapid transit systems [J]. IEEE Intelligent on Transport Systerms, 2012, 6(1): 58-66.

(编辑蒋学东)

Research on energy-saving operation strategy for high-speed train

SONG Wenting1, TAN Min2, CAI Wenchuan1, FAN Liqian3

(1. Center for Intelligent Systems and Renewable Energy, Beijing Jiaotong University, Beijing 100044, China;2. School of Automation, Chongqing University, Chongqing 400044, China;3. State Key Laboratory of Rail Control and Safety, Beijing Jiaotong University, Beijing 100044, China)

Abstract：The energy-saving running of high-speed train was taken as a research target, in which the train traction characteristic and railway conditions were fully considered. The train operation model was established under the constraint of fixed time, and an energy-saving operation strategy for optimizing the speed curve was proposed. At first, combination optimization technique and genetic algorithm were introduced to search the optimal combination sequence of speed codes for subsections, thus the model solution problem was transformed into an optimization problem and the energy-saving operation range of train speed was determined. Then on the basis of this, the principle of changing acceleration one time on a slope was proposed to make full use of the energy-saving advantage of a slope, in tandem with traction, cruise, coast and braking operation modes. Finally, the running speed curve with minimal energy consumption was obtained, which guided the train running between the two successive stations. In order to verify the effectiveness of the proposed strategy, operation of CHR-3 on high-speed railway was simulated.

Key words：high-speed train; energy-saving strategy; combination optimization technique; genetic algorithm; gradient

中图分类号：TB24

文献标志码：A

文章编号：1672-7029(2016)03-0423-07

通讯作者：蔡文川(1978-)，男，重庆人，博士研究生，从事高速列车安全与控制的研究；E-mail：wchcai@bjtu.edu.cn

基金项目：国家自然科学基金重点资助项目(61134001)；国家自然科学基金青年科学基金资助项目(61203124)

收稿日期：2015-08-11