考虑轮对柔性的车轮疲劳寿命研究

吴正习，石广田

(兰州交通大学 机电工程学院，甘肃 兰州 730070)



考虑轮对柔性的车轮疲劳寿命研究

吴正习，石广田

(兰州交通大学 机电工程学院，甘肃 兰州 730070)

摘要:以CRH2型动车组拖车车轮为研究对象，建立考虑轮对柔性的车辆系统刚柔耦合动力学模型，利用有限元法和Palmgren-Miner准则对车轮的疲劳寿命进行研究。利用有限元软件ANSYS建立轮对的有限元模型并生成轮对子结构模型；利用多体动力学分析软件SIMAPCK建立包含柔性轮对的车辆系统刚柔耦合动力学模型，得到轮对的动力学响应和受到的动荷载时间历程，并与车辆系统多刚体动力学模型的结果对比；基于名义应力和Palmgren-Miner准则对车轮的疲劳寿命进行研究。研究结果表明：考虑轮对柔性的车辆系统动力学模型能够得到更准确的车轮受到的动载荷时间历程；车轮首先发生疲劳破坏的部位发生在辐板和轮辋以及轮毂过度处，属非比例多轴疲劳破坏，并首先在辐板表面形成裂纹并逐渐向内扩展；车轮的疲劳寿命远大于设计要求的使用年限，大部分未磨耗的到限的车轮经探伤处理后可以回收再利用。

关键词：疲劳寿命；有限元法；柔性轮对；刚柔耦合动力学模型

铁道车辆部件当中，车轮是承载条件最为恶劣的部件之一，事实证明车轮的疲劳失效会引发灾难性的后果。因此，在设计初期对其疲劳寿命进行研究显得尤为重要。由于车轮形状和所受荷载的比较复杂，采用实验的方法对其疲劳寿命进行评估费用较高，因此采用合理高效的仿真方法准确地对车轮的疲劳寿命进行预测无疑是经济的。目前，汽车等行业已逐步将多体系统动力学分析手段引入到产品结构疲劳设计，部分代替耐久试验，取得了显著的成果和经济效益[1-3]。在动力学仿真分析中，是否考虑轮对结构的柔性对其本身的动力学性能和所受荷载分析有显著的影响[4]。目前，国内外学者已经在轮轨噪声、车辆横向稳定性、轮轨接触力等方面的研究中考虑轮对的柔性。刘韦等[5]研究了考虑轮对柔性对轮轨力和车轮磨耗的影响；缪炳荣等[6]提出了结合多体动力学和有限元法对结构进行疲劳寿命仿真的方法并以车体列举了算例；徐传来等[7]选择了Crossland准则、Dang Van准则、Sine准则和Kakuno-kawada准则对辐板孔区域的疲劳强度进行了研究。在此，本文首先建立考虑轮对柔性的车辆系统刚柔耦合动力学模型，以准确地获得车轮所受到的载荷时间历程，然后采用有限元的方法分析车轮在载荷时间历程作用下的应力分布，最后利用Palmgren-Miner损伤累计规则对其疲劳寿命进行研究，以缩短轨道车轮的开发周期和成本。

1车轮疲劳强度校核

采用有限元软件ANSYS对车轮进行疲劳强度校核；首先考虑轮轴过盈配合对车轮疲劳强度的影响，确保设计模型符合标准疲劳强度要求。其次，获取车轮应力分布云图。

1.1轮轴过盈配合分析

以CRH2高速动车组拖车轮对为研究对象。其轴重为12.5 t,车轮采用UIC标准材料R8T钢，轮对的材料属性及有限元模型采用的单元类型如表1 所示，轮对的有限元模型如图1所示。

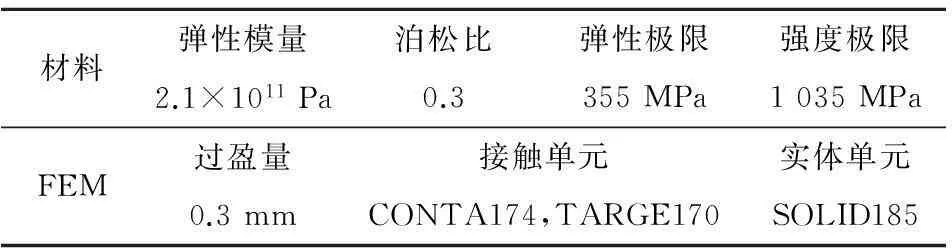
表1　轮对材料和有限元模型单元类型

图1　轮对有限元模型Fig.1 FEM of wheelset

在ANSYS中对轮对过盈配合引起的应力分布进行分析，如图2所示。图2(a)为Von_Mises应力分布，最大应力为311.73 MPa，出现在距轮毂边缘外侧10 mm处，小于RT8钢材料的弹性极限，过盈配合能满足连接强度要求。图2(b)显示过盈装配在轮轴接触面上产生的法向应力为66.924 MPa，在后文的疲劳强度校核中将按照预应力来处理[8]。

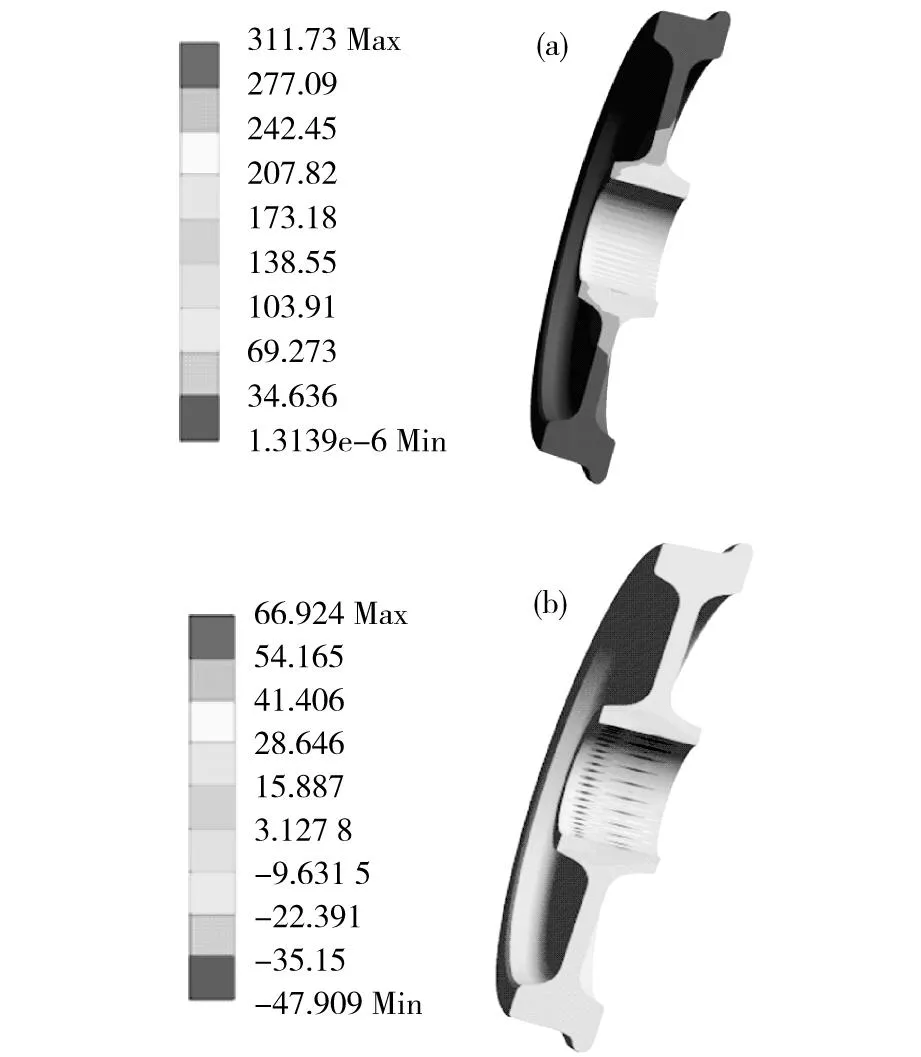
MPa(a) Von_Mises应力分布；(b)法向应力分布图2　0.3 mm过盈配合分析结果Fig.2 Stress distributions of wheel with 0.3 mm interference fit

1.2疲劳强度校核

依照欧洲标准委员会颁布的EN 13979-1-2003[9]中规定的车轮强度校核时所需要的载荷参量和加载位置施加载荷，如图3和表2所示。分别按照直线、曲线和道岔3种工况对车轮进行校核[10]，分析结果如图4所示。图4(a)为直线工况下车轮的应力分布，结果显示最大Von_Mises应力为15.155 MPa，出现在车轮内侧辐板与轮辋的过渡部位。图4(b)为曲线工况下车轮的应力分布，结果显示最大Von_Mises应力为98.433 MPa，出现在车轮外侧辐板与轮毂过渡部位。图4(c)为道岔工况下车轮的应力分布，结果显示最大Von_Mises应力为69.335 MPa，出现在车轮内侧辐板与轮毂的过渡部位。上述3种工况的动应力范围均小于车轮许允动应力范围，最大Von_Mises应力小于车轮材料的弹性极限，说明车轮的设计满足疲劳强度要求。

图3　不同工况的加载位置Fig.3 Load positions under different conditions

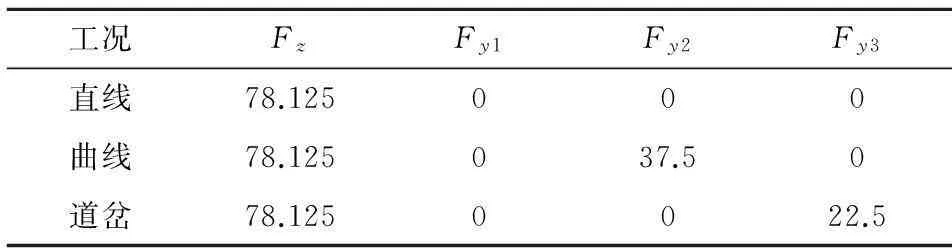
kN

单位：MPa(a) 直线工况下应力分布；(b) 曲线工况下应力分布；(c) 道岔工况下应力分布图4　3种工况下疲劳强度校核Fig.4 Fatigue strength cheecked under three conditions

2车辆系统动力学模型

建立刚柔耦合车辆动力学模型时，首先利用ANSYS对轮对进行子结构分析以提取柔性体信息；然后，将轮对的柔性体信息导入多体动力学软件SIMPACK中[11-12]，建立柔性轮对的刚柔耦合动力学模型。为了体现考虑轮对柔性对车轮所受荷载和动力学响应的影响，将建立车辆的多刚体动力学模型。对仿真结果进行对比分析。

2.1轮对子结构分析

ANSYS和SIMPACK分别用节点和标志点坐标表示柔性体形变，利用Block Lanczos法缩减轮对的质量矩阵、刚度矩阵和自由度以生成轮对子结构模型，提取轮对的质量矩阵和刚度矩阵等柔性体信息。轮对子结构模型如图5所示，共132个主节点，396个主自由度。

图5　轮对子结构模型Fig.5 Substructure model of wheelset

2.2多体动力学建模

根据CRH2拖车的动力学参数建立车辆系统动力学模型，并将轮对的柔性体信息导入定义轮轨接触关系，柔性轮对与构架通过表示一系悬挂装置的线性弹簧阻尼相互作用[13]，轮对的动力学方程为

(1)

式中：{F0}为载荷向量；[M]，[K]和 [C]分别为柔性轮对的质量矩阵、刚度矩阵和阻尼矩阵。将柔性轮对的动力学模型以子结构的方式导入构架模型中，然后构架再以子结构方式导入车辆模型中，至此就建立了轮对为柔性的车辆系统刚柔耦合动力学模型。建立的车辆系统刚柔耦合动力学模型如图6所示。

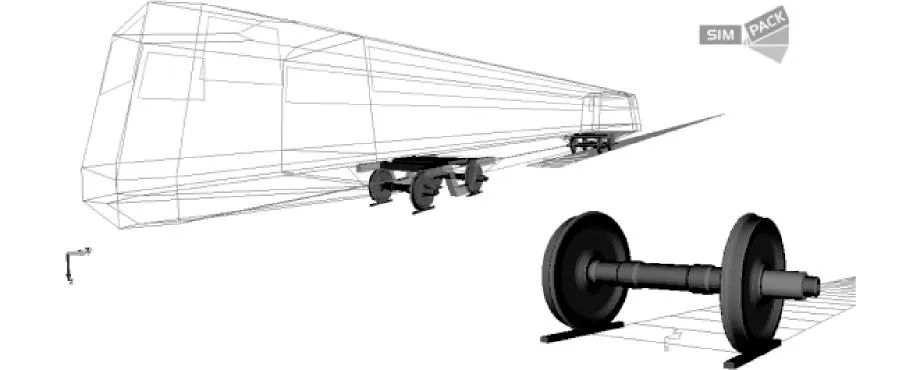
图6　柔性轮对的车辆系统刚柔耦合模型Fig.6 Rigid-flexible coupling dynamics mode of vehicle with flexiable wheelsets

模拟2种模型以运营速度在设定好的轨道上运行，以德国低干扰谱作为轨道激励[14-15]，图7是车速为200 km/h时，车辆系统动力学模型分别为多刚体动力学模型和刚柔耦合动力学模型时轮对的垂向和横向振动加速度。从图7(a)可以看出，柔性轮对的垂向振动加速度最大值几乎是刚性轮对的2倍，柔性轮对的横向振动加速度的最大值也明显大于刚性轮对的。这说明考虑轮对的柔性对其自身的动力学响应有显著的影响，在分析轮对和车轮的动力学问题时考虑轮对的柔性是非常有必要的，也更符合实际情况，因此采用考虑轮对柔性的动力学结果研究车轮的疲劳寿命更加符合实际情况。

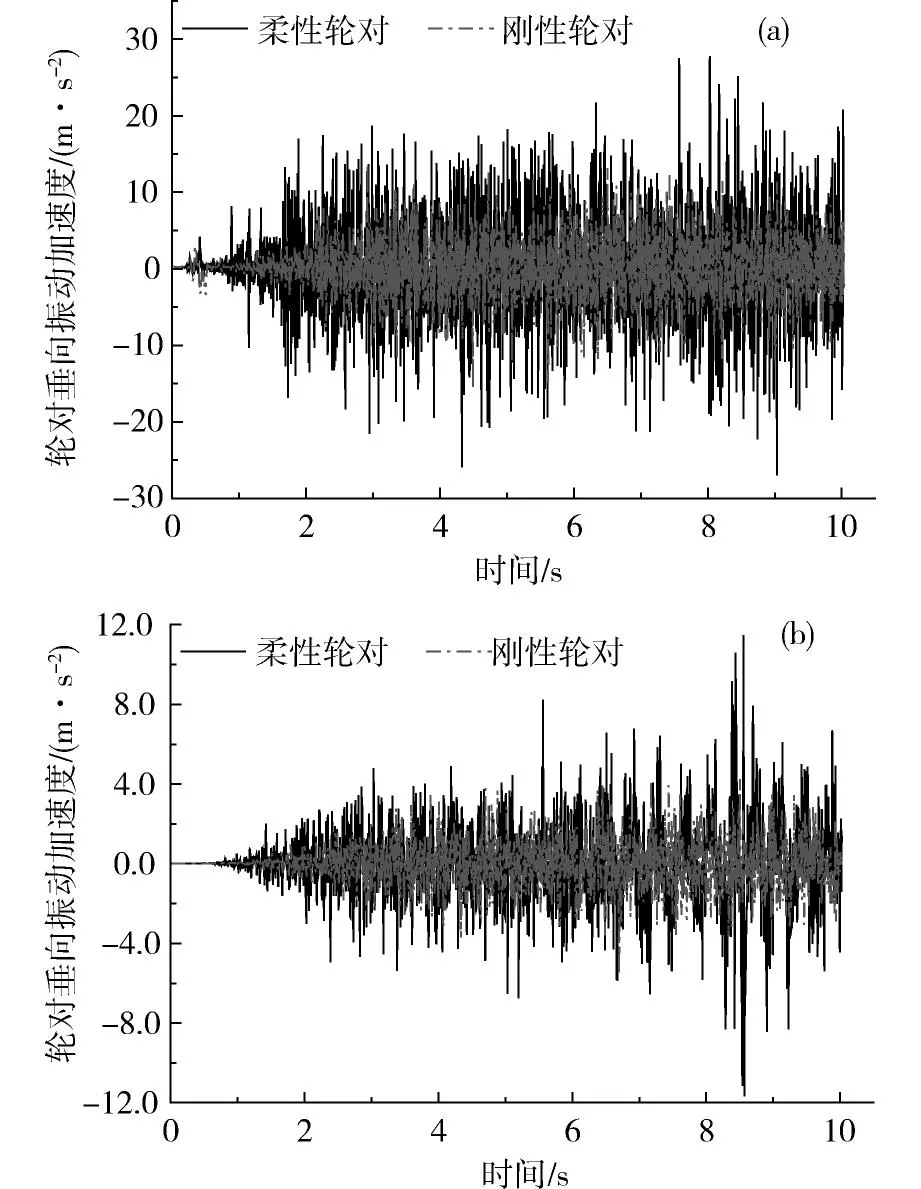
(a) 轮对垂向振动加速度；(b) 轮对横向振动加速度图7　轮对振动加速度对比Fig.7 Comparison of vibration acceleration of wheelset

2.3载荷时间历程

通过上述建立的车辆系统刚柔耦合动力学模型可以得到车轮受到的垂向动荷载和横向动荷载，以用于分析车轮疲劳寿命。由于高速动车组在运营过程中多数时间是在直线和常用曲线上行驶，所以本文取2种典型工况下车轮受到的动荷载分析车轮的疲劳寿命。工况1：直线段，车辆250 km/h的速度运行；工况2：常用的半径为6 000 m的曲线段(包括250 m的缓和曲线)，车辆以以200 km/h的速度运行。图8给出了2种工况下一位外侧车轮所受的垂向动荷载和横向动荷载时间历程。

(a) 直线工况；(b) 曲线工况载图8　车轮载荷时间历程Fig.8 Time historys of loads applied on wheel

3车轮疲劳寿命分析

采用雨流计数法对车轮受到的载荷时间历程进行循环计数，以将其不规则的应力或应变的历程转换为等效的常幅循环[16]；然后，根据图4的车轮应力分布云图，基于名义应力结合Palmgren-Miner准则研究车轮的疲劳寿命。由于车轮的自振频率大于线路激扰频率和车辆系统的固有频率，在这种情况下可以近似认为车轮上各点的响应振幅动应力放大系数接近1，响应的相位差接近0。 这样输入车轮的动载荷与其动应力响应之间是同相位同频率的，其幅值之比为定值，即静载荷与静应力应变之间的比例系数。因此计算车轮上各点的应力应变响应时可采用线性叠加原理，整个应力范围的总损伤可以通过每个应力范围的应力产生的损伤求和计算，计则车轮的损伤的数学公式为：

(2)

式中：(Nf)i是导致车轮结构疲劳失效的循环数；ni是每个应力范围下的循环数；ns是总应力范围循环数。根据车轮材料R8T钢的S-N特性曲线，用Goodman经验公式对其进行修正。采用基于有限元应力分析的结构安全因子疲劳寿命分析，以获得车轮危险点的疲劳寿命计算结果。先求得每种工况下车轮的损伤量，然后将各工况下的损伤量乘以各工况的比重，求和后再取倒数就得到车轮的疲劳寿命，可以表达为：

(3)

式中：i为各工况；n为工况总数；Di为第i工况运行所产生的损伤量；Pi为第i工况所占的比重，L为构件的寿命。车轮在的寿命分布云图如图10所示，表3为曲线工况和直线工况下下前10个危险节点的寿命结果。图10(a)为曲线工况下车轮寿命分布云图，图10(b)为直线工况下寿命分布云图。

从图10可以看出，车轮的疲劳破坏首先发生在轮毂和轮辋与辐板过渡区域，曲线工况下发生破坏的载荷循环数为1.43×107次，直线工况下为5.94×107次。假设该车辆运营区间内直线与曲线之比为1.3∶1，每个工况下损伤最大、寿命最短的位置代表了各工况下整个车轮的寿命，根据每个工况所占的比例按照公式(3)得到车轮的总寿命为4千万km以上。

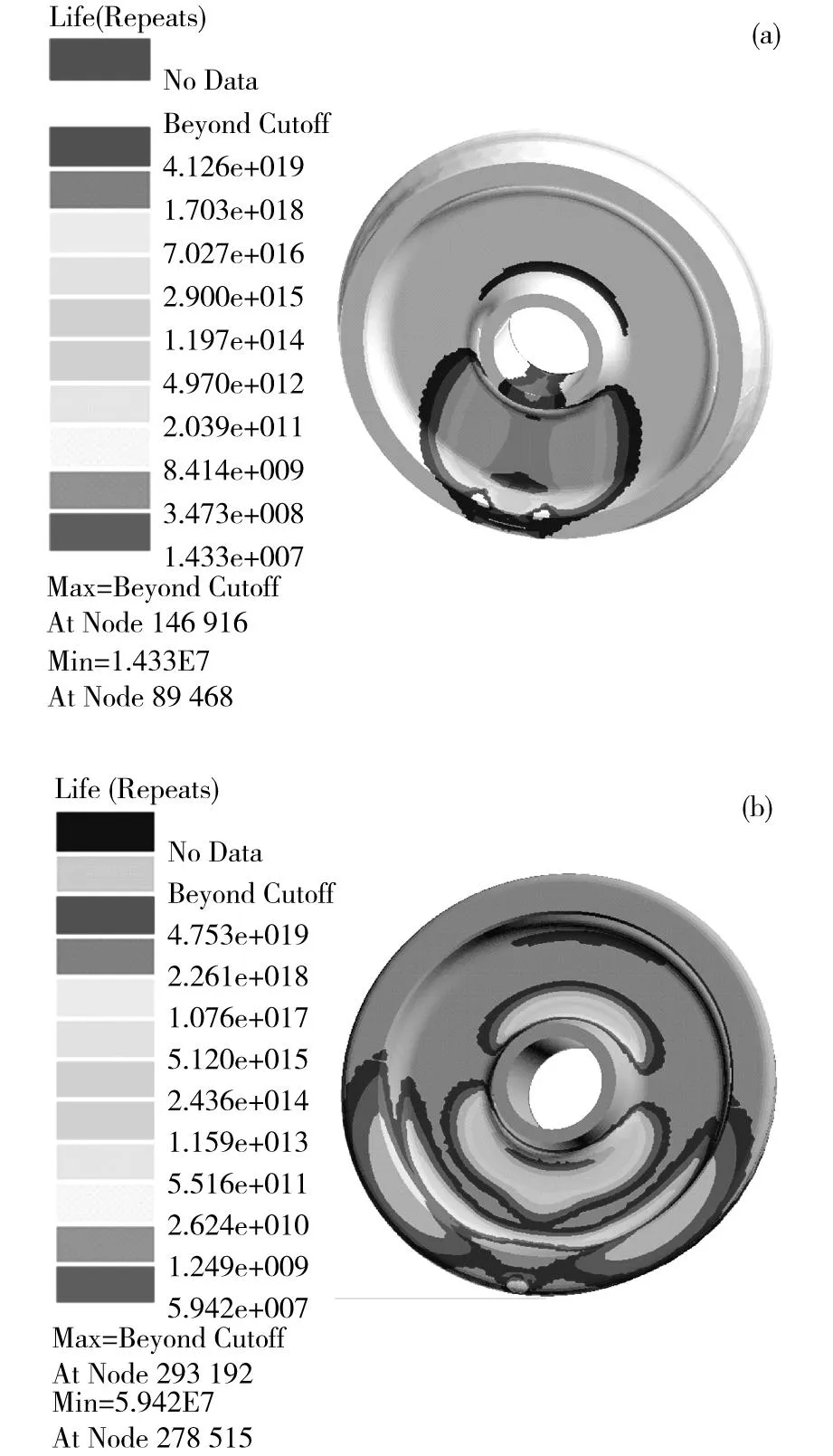
(a) 曲线工况寿命云图；(b) 直线工况寿命云图图10　车轮疲劳寿命云图Fig.10 Fatigue life distribution of wheel

按照CRH2型车每年运行40万 km，运营25 a计算，车轮的疲劳寿命远大于设计要求的使用年限。所以，在车轮踏面经过磨耗需要镟修时，采用经济型镟修法能有效增多车轮的镟修次数，提高车轮的行驶里程。另外，从仿真结果来看，车轮的设计寿命远大于实际规定的使用年限，所以，已经退役的车轮中，如果不是磨耗到限，经过探伤后无裂纹的，其实是可以回收再利用的，以免资源浪费。

利用二轴比的标准偏差可以表征车轮的应力载荷是否成比例；当二轴比标准偏差的值较小或接近于0时，代表比例载荷，否则为非比例载荷。从表3中名义二轴比的值来看，车轮大部分区域的名义二轴比接近于0，为单轴应力状态。在轮辋和辐板过度区域都处在严重的二轴状态，属于非比例多轴状态。在过渡区域的表面上，二轴比为负，裂纹萌生的最大剪应力平面。在初期，裂纹主要在表面扩展，随后转化为最大主应力的法线方向，即A型裂纹。所以在对车轮进行探伤时，应该重点关注辐板和轮辋以及轮毂的过度区域。

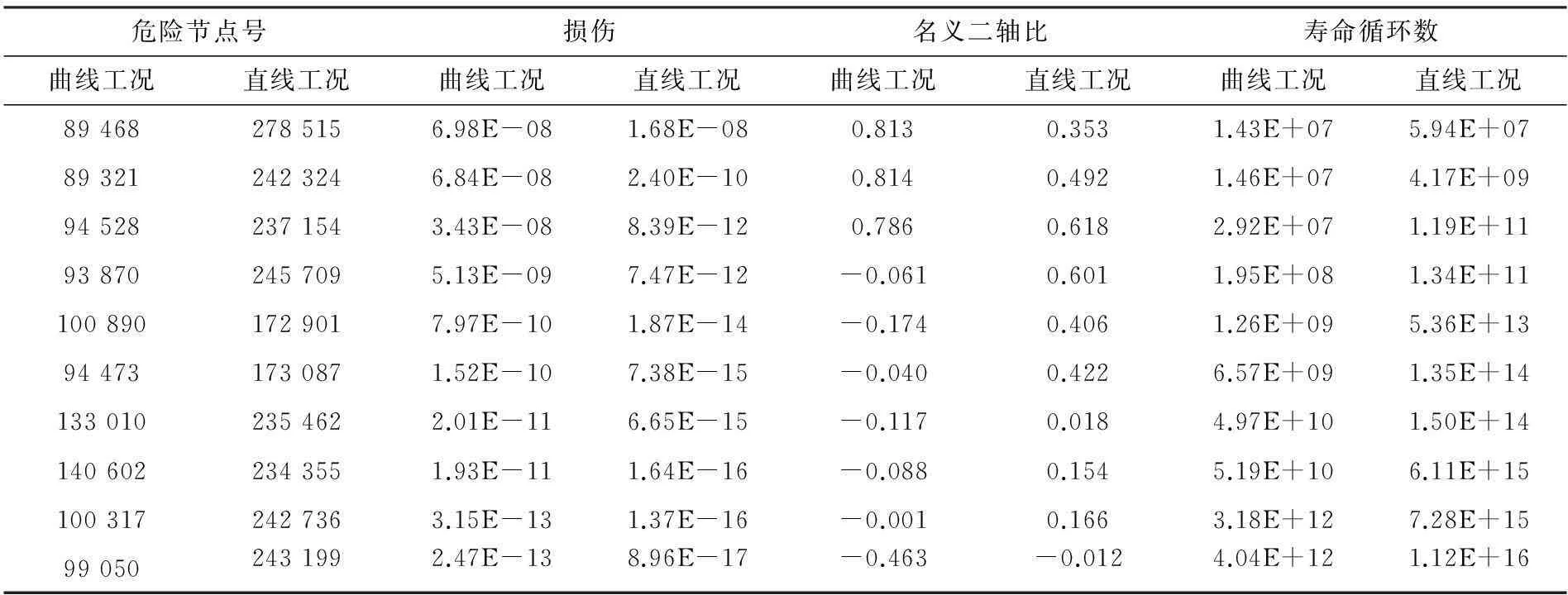
表3　前10个危险节点的计算结果

4结论

1)考虑轮对的柔性，建立了刚性轮对的刚体系统动力学模型和柔性轮对的刚柔耦合模型。通过对比发现，柔性轮对的振动加速度远大于刚性轮对的，因此在分析车轮的疲劳寿命时，建立考虑轮对柔性的车辆系统动力学模型以获取车轮动载荷时间历程，是非常有必要的。

2)利用有限元法和Palmgren-Miner准则，对车轮的疲劳寿命进行分析，结果表明车轮的疲劳寿命远大于设计要求的使用年限。所以大部分未磨耗的到限的车轮经探伤处理后可以回收再利用。建议采用经济型车轮踏面镟修法能有效提高车轮的镟修次数和行驶里程，避免资源浪费。

3)通过名义二轴比数据分析，得出车轮首先发生疲劳破坏的部位发生在辐板和轮辋以及轮毂过度处，该处为车轮的最薄弱部位，属非比例多轴疲劳破坏，并首先在辐板表面形成裂纹并逐渐向内扩展。

参考文献：

[1] Luo R K, Gabbitasb L, Brickle B V. Fatigue life evaluation of a railway vehicle bogie using an integrated dynamic simulation[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1994, 208(2):123-132.

[2] Stefan Dietz, Helmuth Netter, Delf Sachau. Fatigue life perdiction of a railway bogie under dynamic loads through simulation[J]. Vehicle System Dynamics, 1998, 29(6): 385-402.

[3] SU Hong. Automotive CAE durability analysis using random vibration approach[C]// MSC 2nd Worldwide Automotive Conference. Dearborn: MI, 2000: 43-56.

[4] Juren A, Ingi K, Gunter S. Simulation of a railway vehicle's running behaviour: how elastic wheelset influence the simulation results[J]. Vehicle System Dynamics, 2004, 41(Suppl 1): 242-251.

[5] 刘韦, 马卫华, 罗世辉,等.考虑轮对弹性的车轮振动及轮对多边形化对轮轨力影响的研究[J]. 铁道学报, 2013, 35(6):28-34.

LIU Wei, MA Weihua, LUO Shihui, et al. Research on influence of wheel vibration and wheel pologonization on wheel-rail force in consideration of wheelset elasticity[J]. Journal of the China Railway Society, 2013, 35(6): 28-34.

[6] 缪炳荣, 张卫华, 肖守讷, 等.基于多体动力学和有限元法的车体结构疲劳寿命仿真[J]. 铁道学报, 2007, 29(4):38-42.

MIAO Bingrong, ZHANG Weihua, XIAO Shoune, et al. Carbody fatigue life simulation based on multibody dynamics and FEM[J]. Journal of the China Railway Society, 2007, 29(4):38-42.

[7] 徐传来, 米彩盈. 高速动车组动力轮对车轮疲劳强度研究[J]. 计算机仿真, 2014, 31(6):158-163.

XU Chuanlai, MI Caiying. Fatigue strength of wheel of high-speed EMU power wheelset[J]. Computer Simulation, 2014, 31(6):158-163.

[8] 胡宝义. 动车组车轮和车轴强度分析[D].北京:北京交通大学, 2008:1-91.

HU Baoyi. Wheels and axles strength analysis of electric multiple unit[D]. Beijing: Beijing Jiaotong University, 2008:1-91.

[9] BS EN 13979-1-2003. Railway application wheelset and bogies-monoblock wheels-technical approval proceedure-part1: Forged and rolled wheels[S]. European Committee for Standardization, 2003.

[10] 梁红琴, 赵永翔, 杨冰,等.高速动车组拖车车轮疲劳强度研究[J]. 机车电传动, 2013, 2:18-20.

LIANG Hongqin, ZHAO Yongxiang, YANG Bing, et al. Fatigue strength analysis and check of high-speed EMUs trailer wheel[J]. Electric Drive for Locomotives, 2013(2): 18-20.

[11] 万鹏.考虑轮对弹性时车辆系统动力学建模与仿真分析[D]. 成都:西南交通大学, 2008:1-85.

WAN Peng. Modelling and simulation analysis of vehicle system dynamics in consideration of the elasticity of wheelsets[D]. Chengdu:Southwest Jiaotong University, 2008:1-85.

[12] 杨亮亮,傅茂海,周尚书,等.刚柔耦合理论在铁道车辆中的应用[J].内燃机车, 2012(10):24-28.

YANG Liangliang, FU Maohai, ZHOU Shangshu, HUANG Xiaocui. The Theory of rigid-flexible coupling be used in railway vehicle[J].Diesel Locomotives, 2012(10):24-28.

[13] 王文静, 孙守光，李强.柔性构架的动应力仿真[J]. 铁道学报, 2013, 35(6):44-49.

WANG Wenjing, SUN Shouguang, LI Qiang. Dynamic stress simulation of flexible bogie frame[J]. Journal of the China Railway Society, 2013, 35(6):13-18.

[14] 丁军君, 李芾, 周张义,等.基于车轮磨耗寿命预测的轨道参数研究[J]. 铁道科学与工程学报, 2014, 10(4):13-18.

DING Junjun, LI Fu, ZHOU Zhangyi, et al. Parametric study of the railway based on wheel wear lifetime predication[J]. Journal of Railway Science and Engineering, 2014, 10(4): 13-18.

[15] 高建敏.高速铁路无砟轨道不平顺谱的比较分析[J]. 铁道科学与工程学报,2015,12(4):715-723.

GAO Jianmin. Comparative analysis of power spectrum density of ballastless track irregularities of Chinese high-speed railway[J]. Journal of Railway Science and Engineering, 2015,12(4):715-723.

[16] 吴光强, 李运超, 盛云. 后悬架多轴疲劳寿命预测[J]. 同济大学学报(自然科学版), 2010, 3(6):880-902.

WU Guangqiang, LI Yunchao, SHENG Yun. Multiaxial fatigue life prediction of rear suspension[J]. Journal of Tongji University (Natural Science), 2010, 3(6):880-902.

(编辑阳丽霞)

Fatigue life of railway wheel based on rigid-flexiblecoupling dynamic model of vehicle system

WU Zhengxi, SHI Guangtian

(School of Electromech anical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Abstract:The wheels of the CRH2 trailer are taken as the research object, and a vehicle system dynamic model with flexible wheelsets was established. The finite element method and Palmgren-Miner rule were used to study the fatigue life of wheel. First, the finite element model of wheelset and its substructure model were obtained using finite element software ANSYS. Second, a rigid-flexible coupling dynamic model of vehicle system which contains four flexible wheelsets was established using multi-body dynamics software SIMPACK, andthe time history of loads and the dynamic response applied on the wheelset are obtained. The results were compared with the ones of multi-rigid vehicle system dynamic model. Finally, the fatigue life of wheel were analyzed based on nominal stresses and Plamgren-Miner rule. The results show that the time history of dynamic loads applied on wheels obtained by the vehicle system dynamic model with flexible wheelsets are more accurate ; the fatigue rupture emerges first at the transition between rim and wheel hub and is non-proportional multi-axis destruction. The fatigue life of wheels are longer than designed durable years, so most of wheels which do not reach the limit of abrasion could be recycled after flawdisposition.

Key words:fatigue life; finite element method; flexible wheelset; rigid-flexible dynamic model

中图分类号：U260.33+.1;TP391.9

文献标志码：A

文章编号：1672-7029(2016)03-0557-07

通讯作者：石广田(1962-),男,甘肃天水人，教授,博士,从事轨道交通系统动力学; E-mail:shigt@mail.lzjtu.cn

基金项目：甘肃省财政厅基本科研经费资助项目;兰州交通大学青年科学基金资助项目(2013028)

收稿日期：2015-11-23