基于单应性矩阵剔除SIFT错误匹配点的方法

刘 婷 婷(天津大学 理学院 数学系，天津 300072)



基于单应性矩阵剔除SIFT错误匹配点的方法

刘 婷 婷(天津大学 理学院 数学系，天津 300072)

摘要：根据图像几何变换的单应性矩阵将匹配点一一对应的特点，提出一种基于单应性矩阵的剔除方法.该方法首先利用SIFT进行匹配，得到初始匹配对，进行初步筛选，然后利用相似三角形求出基准单应性矩阵，设定阈值，剔除不满足阈值的匹配点对，最后得到精确匹配点对.通过与RANSAC算法以及结合欧式距离的RANSAC改进算法进行实验比较,该算法具有更高的正确匹配率.

关键词：错误匹配点；单应性矩阵；相似三角形；RANSAC

给定某个场景的一组互相有重叠的局部图像，生成包含着这组局部图像的一幅完整的宽视场图像，称为图像拼接.图像拼接在全景图像的构成、地球卫星照片的合成、3D立体模型的构造、遥感图像处理、医学图像分析和计算机视觉等方面都有很重要的应用[1].图像拼接的主要步骤包括:图像预处理，图像匹配，图像融合.图像匹配是图像拼接的关键环节，直接决定图像拼接的质量与效率.目前图像匹配算法大致分为两大类，第一类是统计匹配方法，主要有平均绝对差度量、均方差度量和基于灰度互相关度量的匹配算法;第二类是基于特征的匹配方法[1].基于灰度的匹配方法不需要对图像进行特征提取，直接利用图像的灰度信息，能够提高估计的精度和鲁棒性，但是计算量较大，且对噪声敏感[2].基于特征的匹配方法是目前主要运用的图像匹配方法，此类方法稳健性强，计算量小，适用于多源图像配准问题.基于不变特征的匹配是近年来图像匹配技术的研究热点.

特征匹配是基于特征匹配方法的关键，目前解决这类问题的方法主要包括图匹配方法[3-4]、谱方法[5-6]和基于局部描述子的方法[7-9]等.近年来，基于局部描述子的方法应用较为广泛.传统的基于局部描述子的方法是基于角点或边缘的匹配，对环境的适应能力差.Lowe总结提出了一种基于尺度空间，对图像放缩、旋转甚至仿射变换具有强鲁棒性的图像局部特征描述子—SIFT[7](Scale Invariant Feature Transform，尺度不变特征变换，简称SIFT)，SIFT是实际问题中应用最为广泛的局部特征描述子.

在大多数情况下，SIFT都可以得到满意的匹配结果.然而，当图像间具有相似结构时，SIFT匹配就会产生大量的错误匹配点.这些错误点的存在对图像匹配和图像拼接的效果有直接影响.因此，研究如何剔除SIFT的错误匹配点具有重要意义.

RANSAC(RANdom Sample Consensus，随机采样一致性)方法是由Fischler和Bolles于1981提出的鲁棒方法.RANSAC[10]目前常用于剔除错误匹配点，但仍不能完全剔除错误匹配点.此外，由于算法本身带有随机性，一旦样本点选取错误将导致剔除错匹配点的效果变差，可能导致图像处理后续步骤的失败.Kasar T提出了一种改进算法[11]，利用欧式距离比值对初始的特征点对进行筛选，提高了匹配精度，但仍然存在大量错匹配点，RANSAC算法执行效率仍比较低.特征点的检测与匹配是图像匹配的基础，图像匹配以及图像拼接效果的保障是足够的特征点与较高的正确匹配率.

本文提出了一种剔除错误SIFT匹配点的方法，在剔除“一对多”类型误匹配点的基础上，首先根据三角形的相似性[12]选取正确基准点，由基准点估计基准单应性矩阵，根据单应矩阵投影后的对应点之间的欧氏距离是否满足阈值来剔除错误匹配点.该方法与RANSAC以及结合欧式比值的RANSAC相比，筛选后的匹配点中正确的匹配点所占比例更高，同时避免了RANSAC中的随机性造成不好的实验结果.

1SIFT特征点检测及匹配算法

SIFT是 1999 年由 Lowe 正式提出的一种基于尺度空间的图像局部特征描述方法，并在 2004 年被加以完善. 利用 SIFT 算法提取图像局部特征主要包括 4 个步骤:尺度空间极值点检测、特征点精确定位、特征点方向分配、特征点描述.具体步骤如下[7]：

1)尺度空间极值点检测.利用一系列尺度因子乘以高斯函数对原始图像进行滤波，建立尺度空间，通过对图像尺度空间进行下采样，建立图像的高斯金字塔;然后，将高斯金字塔的相邻层相减，得到图像的高斯差分金字塔.利用上下相邻尺度的图像求取局部极值来确定候选极值点.

2)特征点精确定位. 利用尺度空间函数D(x,y,σ)的泰勒展开式来对DoG(Difference-of-Gaussian，高斯差分)空间中的极值点进行精确定位[7].为了提高 SIFT 特征点的稳定性，候选特征点被检测出来以后，还需要经过进一步的处理，以除去那些对比度低的极值点和边缘响应点.

3)特征点方向分配. 利用关键点邻域某一范围内像素点的梯度方向分布特性为每个特征点指定一个主方向，然后相对于此方向来生成特征向量.每个特征点包含位置、尺度和方向等三方面的信息，由此确定一个SIFT特征区域.

4)特征点描述.首先将图像的坐标轴旋转至特征点的主方向，然后对每个特征点使用共16个种子点来描述，形成128维的SIFT特征描述子.

SIFT特征点的匹配从本质上来讲是高维空间中特征向量的最近邻搜索问题.基本SIFT匹配方法有穷举搜索、局部敏感哈希(Locality-Sensitive Hashing,LSH))和最优节点优先(Best Bin First,BBF).在SIFT算法的实际应用过程中, SIFT特征点的匹配是最重要的步骤之一.

由于SITF特征描述子只利用了特征点的局部信息，当待匹配的图像中存在相似的结构时，那些散落在这些相似结构中的特征点所对应的局部信息具有很高的相似性，若此时仅利用这些局部信息进行匹配，很容易产生误匹配[13].如果匹配的SIFT特征点中包含大量错误匹配点，直接进行图像处理的后续步骤将会产生错误结果，或者直接影响实验效果，因此剔除错误匹配点就至关重要.

2剔除错误匹配点的算法

2.1“一对多”错误匹配点

SIFT的错误匹配点有一种特殊类型的错匹配，也是一种常见的错匹配是“一对多”(或“多对一”)的类型[12].即一幅图像中的某一个特征点与匹配图像中的两个或多个特征点匹配.若约束一个特征点只能与一个特征点对应，便可去除“一对多”类型的特征点.图1中展示了剔除“一对多”类型错误匹配点的前后对比图(只用圆圈标注了部分错匹配点).

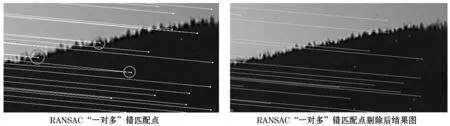
图1　“一对多”错匹配点剔除前后对比图

2.2基于单应性矩阵的剔除方法

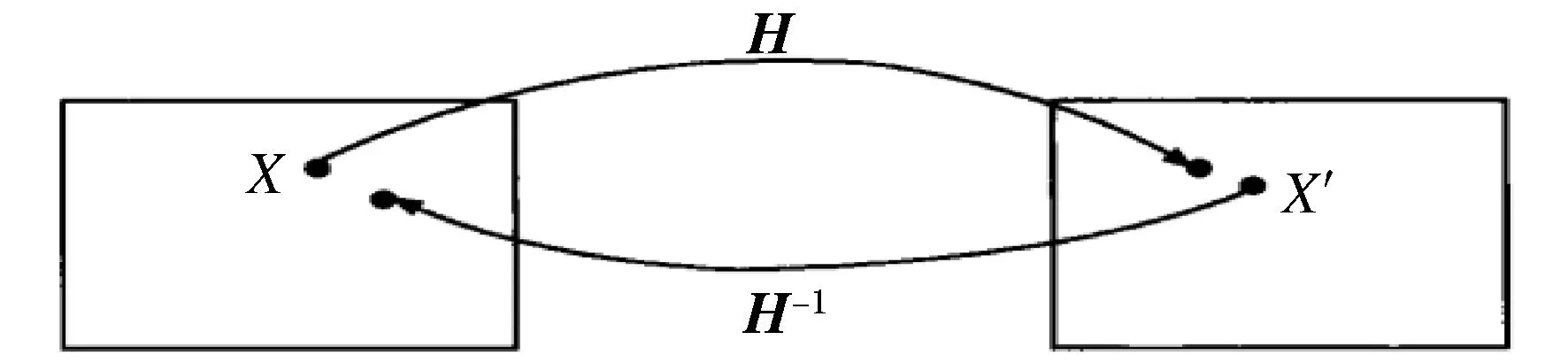
给定两幅有重叠区域的图像I和I′上的两点x和x′，H是两幅图像变换的单应矩阵，则有x′·Hx，其中“·”表示成比例相等.估计单应性矩阵只需4对对应点即可求出[14]，但精确度较低.对应点对越多，单应性矩阵估计越精确.

该算法的步骤是在剔除“一对多”类型的错匹配点的基础上进行的.在较大畸变不存在的情况下，正确匹配点之间可近似利用同一单应矩阵对应匹配点(近似对应)，而错误匹配点与正确匹配点之间变换的单应矩阵是不同的.此外，多个正确的匹配点在基准图和观测图中的相对位置都是固定的，任意的三个正确匹配点在观测图中形成的三角形和对应点在基准图中形成的三角形是相似的(近似满足)[12]，如图2所示.

图2　正确匹配点形成的相似三角形

基于上述特点，本文提出基于单应性矩阵剔除SIFT错误匹配点的算法，具体算法如下:

1)利用STFT算法检测特征点，并进行匹配；

2)剔除匹配点中“一对多”类型的错误匹配点；

3)利用正确匹配对应点形成相似三角形的特点选取出正确匹配点对(至少4对)[10]：

对任意一对匹配点Ri、Si，利用k-d树找到相邻的两对匹配点Ri+1，Ri+2,Si+1,Si+2,判断三角形RiRi+1Ri+2和三角形S1Si+1Si+2对边夹角是否相同，即是否为相似三角形.这里的相似是近似相似，只需对边夹角的余弦值之差小于阈值c.即当对边夹角满足

|cosθ1-cosθ2|

(1)

就认为两三角形相似.其中，阈值c=0.05.如果满足，就保留Ri+1,Ri+2和Si+1,Si+2作为基准点，在剩余匹配点对中继续寻找满足相似三角形条件的匹配点对，直到所有满足相似三角形的正确匹配点对被找到为止；

4)根据已找到的正确匹配点对估计两幅图像几何变换的单应矩阵H，作为基准单应性矩阵.从剩余的匹配点对中找到满足欧式距离小于阈值的正确匹配点对.选择对称转移误差作为距离函数d.

d(x,x′)=‖x-Hx′‖+‖x′-H-1x‖

(2)

其中，x和x′分别为两幅图像中的对应点;‖·‖为两点之间的欧式距离，如图3所示[15].对于一对匹配点Rk,Sk，如果d(Rk,Sk)<δ，则认为Rk,Sk是一对正确的匹配点.否则，将这对匹配点剔除.其中，δ=1.8是根据实验的经验取值.

3实验结果及分析

3.1实验结果

本文进行测试实验的图片来自Groundtruth图形库中的图片，所选取匹配的图像之间不存在较大畸变和视差.图4中两组图像的左中右图分别是采用了RANSAC算法、结合欧式比值的改进的RANSAC算法和本文算法处理后的结果.

在处理器为Inter(R)Core(TM)i5-3470sCPU@2.90GHz，内存为4GB配置的电脑上，运行软件是MATLABR2014a的条件下实验数据如表1所示.

3.2实验结果分析

从上述实验数据中可以得出如下结论:本文的算法在筛选匹配点对的三种算法中，正确率是最高的；RANSAC虽然保留了较多的匹配点对，但是其中仍然存在大量的错误匹配点对；结合欧式距离的RANSAC在时间效率上相比较RANSAC更高，但是正确率仍然很低.

4结语

本文提出了一种基于单应性矩阵剔除SIFT错误匹配点的算法.该算法几乎可以剔除所有的错误匹配点.与RANSAC算法以及结合欧式距离改进的RANSAC算法相比，具有较高的正确匹配率，为图像拼接等后续图像处理奠定了坚实的基础，保证了图像处理的效果.

图3　对称转移误差

图4　三种算法剔除效果对比

所用图片匹配特征点对RANSAC欧式比值+RANSAC本文算法过滤后的特征点对/精确匹配的特征点对/计算时间265115/76/3.9628s70/47/3.3526s137/137/2.4044sColumbiagorge746706/523/11.8571s417/276/7.0536s512/512/353.7531s435408/273/6.2236s248/164/3.9143s269/269/29.1884sYellowstone269202/174/3.9158s121/102/3.2062s197/197/5.6833s486443/354/6.9139s279/197/4.7162s354/354/66.0381s280238/189/4.4375s145/111/3.5660s190/188/7.8277s360305/265/5.6217s192/160/3.7927s273/271/18.3121s

参考文献：

[1]韩晓微. 数字图像融合技术[M]. 沈阳: 东北大学出版社, 2010.

[2]LEWIS J P. Fast Template Matching[C]// Proc of Vision Interface’95, 1995. 120-123.

[3]CAETANO T, MCAULEY J J, LI C,etal. Learning graph matching [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(6): 1048-1058.

[4]BUNKE H, RIESEN K. Recent advances in graph-based pattern recognition with applications in document analysis [J]. Pattern Recognition, 2011, 44(5): 1057-1067.

[5]JAIN V, ZHANG H, KAICK O M. Non-rigid spectral correspondence of triangle meshes [J]. International Journal on Shape Modeling, 2006, 13(1): 101-124.

[6]CARCASSONI M, HANCOCK E R. Spectral correspondence for point pattern matching [J]. Pattern Reconition, 2003, 36(1): 193-204.

[7]LOWE D G. Distinctive image features from scale-invariant keypoints [J]. International Journal of Computer Vision, 2004, 60(2): 91-110.

[8]BAY H, ESS A, TUYTELAARS T,etal. SURF: Speeded up robust features [J]. Computer Vision and Image Understanding, 2008, 110(3): 346-359.

[9]SONG Z L, ZHANG J. Remote sensing image registration based on retrofitted SURF algorithm and trajectories generated from Lissajous figures [J].IEEE Geoscience and Remote Sensing Letters, 2010, 7(3): 491-495.

[10]KIM T J, IM Y J. Automatic satellite image registration by combination of matching and random sample consensus [J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(5): 1111-1117.

[11]KASAR T, RAMAKRISHNAN A G. Block-based feature detection and matching for mosaicing of camera-captured document images[C]// Taibei: IEEE TENCON 2007, 2007. 1-4.

[12]张东兴, 祝明波, 邹建武, 等. 基于相似三角形的SIFT错误匹配点剔除算法研究[J]. 计算机工程与科学, 2012, 34(4): 66-70.

[13]张洁玉, 白小晶, 徐丽燕, 等. 基于空间分布描述符的SIFT误匹配校正方法[J].中国图象图形学报, 2009, 14(7): 1369-1377.

[14]HARTLEY R, ZISSERMAN A. Multiple view geometry in computer vision [M]. London: Cambridge University Press, 2003.

[15]王鑫, 徐立中. 图像目标跟踪技术[M]. 北京: 人民邮电出版社, 2012. 76-77.

Method of eliminate SITF mismatching points based on homography

LIU Ting-ting

(Department of Mathematics, Tianjin University, Tianjin 300072, China)

Abstract：In this paper, a method based on the characteristics of the homograph matrix was presented to eliminate mismatching points. At first, SIFT algorithm was used to extract the feature points and get initial matching. The conduct preliminary screening and calculate the benchmark homograph matrix by using similar triangles. Furthermore, set a threshold value to eliminate matching point pairs that don’t meet the threshold and get accurate corresponding point pairs. Through the contrast experiment with both RANSAC algorithm and improved RANSAC algorithm combined with the Euclidean distance, it was verified the algorithm had higher correct matching rate.

Key words：mismatching points; homograph matrix; similar triangles; RANSAC

中图分类号：TP391

文献标识码：A

文章编号：1672-0946(2016)01-0095-04

作者简介：刘婷婷(1991-)，女，硕士，研究方向：计算机视觉.

收稿日期：2015-04-02.