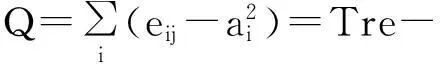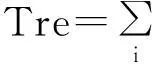一种基于节点重要度的社团划分算法

吴卫江，周　静，李国和

(中国石油大学(北京) 地球物理与信息工程学院，北京 102200)



一种基于节点重要度的社团划分算法

吴卫江，周静*，李国和

(中国石油大学(北京) 地球物理与信息工程学院，北京 102200)

摘要指出了通过挖掘复杂网络中存在的社团结构，可以分析整个复杂网络的拓扑结构和功能，还可以发现网络中隐藏的规律.为了得到最佳社团划分结构，定义了网络的节点重要度矩阵和聚类矩阵，结合图的特征谱平分法和模块度函数，提出了一种基于节点重要度的社团划分算法(CDNIM).通过在空手道俱乐部、海豚关系网络等多个经典数据集上应用，结果表明：该算法能够有效提高发现社团结构的准确率.

关键词复杂网络； 社团结构； 谱平分； 聚类算法； 模块度

Community Partition Algorithm Based on Node Importance

WuWeijiang,ZhouJing,LiGuohe

(China University of Petroleum-Beijing,College of Geophysics and Information Engineering,Beijing 102200,China)

AbstractThis paper points out that through mining the society existed in complex networks, the topological structure and function of complex networks can be analyzed, and the hidden rules can be found either. In order to get the optimal community structure, node importance matrix and clustering matrix are defined, combined the spectral bisection method based on graph and modularity function, an community partition algorithm (CDNIM) based on node importance is proposed. This algorithm is applied in karate club, dolphin networks, and other classical data sets, the result of experiment shows that this algorithm can effectively improve the accuracy of discovering community structure.

Keywordscomplex networks；society structure；spectral bisection method；clustering algorithm；modularity

在现实世界中，存在着各式各样的网络，如科技网、社会网络、生物网等,它们都可以抽象成复杂网络.小世界[1]和无标度[2]特性是研究复杂网络理论的开创性标志，随着人们对复杂网络的研究不断深入，发现复杂网络的另外一个特性，即社团结构[3]特性.复杂网络中的社团结构表征为：存在于单个社团内部的各个节点之间的边较多，分布比较有地域密集性，而社团之间相互连接的边比较少.这种社团结构暗示着同一社团内的节点具有相同的属性或者是有其他相似的方面.对复杂网络进行社团划分，可以更好地了解现实网络中的内部组织结构：依据复杂网络中划分的各个社团的功能，可以推测出整个网络的实际功能；研究网络中某些节点的功能，可以推测在与该节点同一社团内其他节点的功能；研究网络中划分的各个社团之间的联系，可以清晰地认知网络的整体布局.因此，能够有效地挖掘出复杂网络中存在的社团结构，对于现实网络的研究具有非常重要的意义.

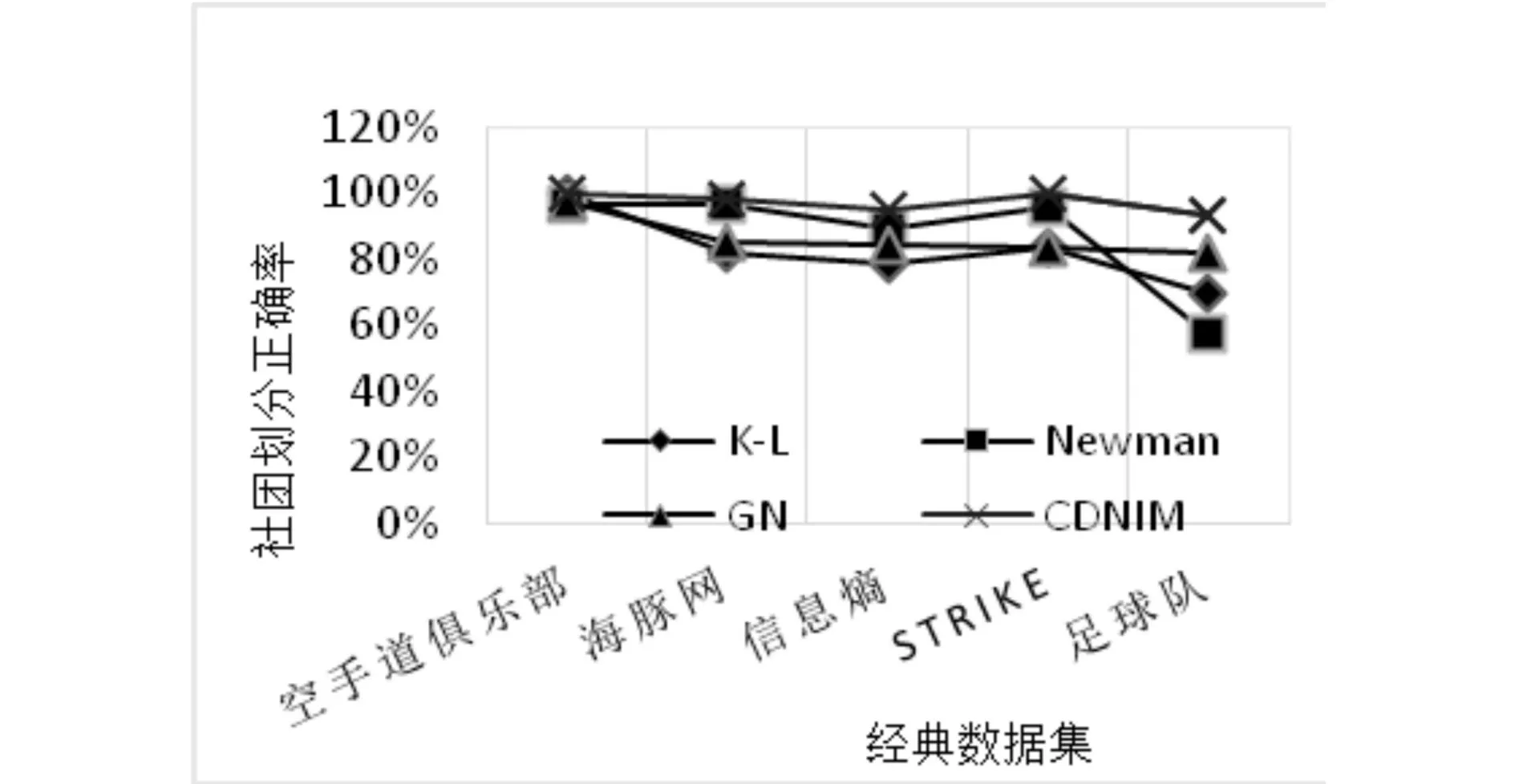
本研究根据谱平分法的启发，定义了网络的节点重要度矩阵，结合聚类分析算法，提出了基于节点重要度的社团划分算法(CDNIM)，用来探测网络中的社团结构.将该算法在经典的数据集上—空手道俱乐部网络、海豚关系网、足球队网络等进行了验证，全部得到了正确的社团划分结果.围绕划分社团的准确率，进一步实验，比较了CDNIM与其他经典的社团发现算法，得出CDNIM算法挖掘复杂网络中的社团结构准确率较高.

1相关定义

在一个无向无权网络G=中，节点集为V，边集为E，节点集V中一对点即对应边集E中的一条边.

定义1：设节点集V={e1,e2,…,en}，令(ei,ej)表示节点ei∈V与节点ej∈V之间的边，边集E⊂{(ei,ej):ei,ej∈V}，那么节点ei的度Di就表示ei的邻居节点的数目，即与该节点连接的其他节点的数目，Di表达式为：

Di=|{(ei,ej):ei,ej∈V;(ei,ej)∈E}|.

(1)

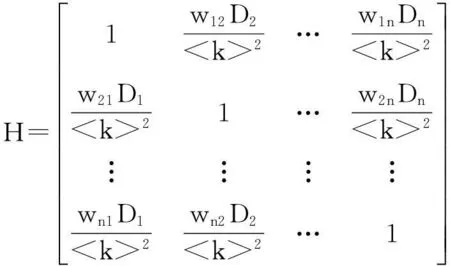
(2)

其中，wij为网络的邻接矩阵中所对应的元素,wij取值为0或1.wij=1，表示网络中的节点i和节点j直接相连；wij=0，表示网络中的节点i和节点j没有直接相连.矩阵中对角线上的元素全部置为1，它表示网络中每个节点对于自身的重要度贡献比值为1.根据定义2，网络的节点重要度矩阵H是网络邻接矩阵的映射.当i≠j时，wij映射成wijDj/2；当i=j时，wij=1.

定义3：为了对网络进行社团划分，将社团划分的问题转化成对网络中各个节点进行k聚类问题.根据谱平分方法的启示，实际上是计算网络节点重要度矩阵H的特征值和特征向量.将节点重要度矩阵H进行行标准化，求其特征值之后将其排序，从中挑选k-1个特征值对应的特征向量((e1,e2,…,ek-1)，其中ei∈Rn,i=1,2,…,k-1)组合成聚类矩阵E.矩阵E的行向量作为n个数据向量形式的待聚类数据.

利用网络的Laplace[5]矩阵进行社团划分是谱平分法[6]的理论基础.网络G的Laplace矩阵L是一个是对称的矩阵，假设矩阵L的n特征向量为0=λ1<λ2<，…,λn，其对应的特征向量为v1

2CDNIM算法

2.1CDNIM算法概述

本文算法定义了节点重要度矩阵H和聚类矩阵E，结合图的谱平分法思想，提出了一种基于节点重要度的社团划分算法(CDNIM).算法CDNIM具体描述如下.

对于一个给定的网络G=，给定一个聚类数目k，基于k-means聚类的复杂网络社团结构探测算法基本步骤如下：

输入：具有n个节点的复杂网络G=，需要划分的社团个数为k；

输出：网络的社团集合S；

(1)计算网络的节点重要度矩阵Hi=wijDi/2；

(2)将节点重要度矩阵H进行行标准化即H1=norw(H)后，求矩阵H1的特征值D和特征向量V；

(3)将特征值排序，选取k-1个特征值所对应的特征向量组成聚类矩阵E；

(4)将聚类矩阵E的行向量作为n个数据向量形式的待聚类数据，调用k-means算法将节点进行聚类.根据聚类得到的划分结果，计算出此时相对应的模块度值Q；

(5)根据以上步骤，可以得到k-1个Q值，社团的最佳社团结构即对应最大的Q值.

2.2网络社团数目k值确定

聚类分析中的k-means算法的k值需要根据经验得到，本文提出的CDNIM算法输入也包含复杂网络中的社团个数k，这里k值需要根据模块度Q值确定.对于一个复杂网络，我们事先并不知道该网络中到底存在多少个社团，更不知道该网络应该被划分成多少个社团才是符合现实情况的.本文算法中的k值可以通过Newman和Girvan提出的模块度函数Q[9]确定，函数Q作为网络划分的一个衡量标准.

综上，网络的社团划分结构决定了模块度的大小，即网络划分的社团结构强度越强，划分质量越好时模块度Q值越大.当CDNIM算法运行结束时，不同的社团划分个数对应不同的模块度Q值，Q值最大时对应的网络社团划分方案就是最佳的社团划分结果，即最佳的k值.

3算法验证及分析

在5个真实数据集上进行实验，验证CDNIM算法的合理性和有效性.实验环境为因特尔酷睿双核P7350处理器，内存2GB，32位Windows 7操作系统，主要编程语言为Java语言以及Matlab编程工具.

3.1实验数据集

(1)Zachary空手道俱乐部.Zachary空手道俱乐部成员关系网络是复杂网络、社团发现技术等领域的典型测试网络数据集，数据集中的各个节点代表俱乐部中的成员，网络中的边代表成员之间的联系[10].网络中的人物关系因为某种原因分裂成了2个小社团.

(2)海豚关系网络.另外一个检测网络社团划分算法的经典数据集是海豚关系网络(Dolphins)[10]，该网络的数据由D．Lusseau 等人提供.网络中的62的节点代表海豚，159条边代表海豚之间有频繁的往来关系.海豚关系网初始分裂为2个社团.

(3)信息熵网络.信息熵网络来自于Martin Rosvall等人的研究，用于研究采用信源和信宿之间的互信息熵最大时所得的复杂网络社团划分算法是否准确.

(4)Strike数据集.Strike数据集描述的是一家锯木厂中不同种族员工之间沟通情况的数据集.该锯木厂的团队领导根据员工之间的沟通频率将网络分为3个社团.

(5)足球队网络.足球队网络中，有115个节点，613条边，节点对应足球队，边表示足球队之间的赛事.这些足球队被分在了12个小组里，每个小组有8～12支球队，在同一小组内的球队之间比赛次数较多.

3.2验证社团个数k值实验结果

表1　CDNIM算法应用在不同的数据集上得到的社团划分个数

3.3CDNIM算法划分足球队网络实验结果

足球队网络中包含12个小组，具体分布见表2.应用本文算法划分足球队网络，网络被划分成k个社团时所对应的模块度值如图1所示.

图1　足球队网络被划分成k个社团时所对应的模块度值Fig.1　Themodularity of that network football is divided intok communities

当网络被划分成12个社团时(即k=12)，模块度达到了最大值，符合实际情况.利用CDNIM算法划分足球队网络的社团结果如表3，总共有8个节点(29,43,59,60,64,91,93,98)划分错误，划分社团的准确率为93.04%.

表2　足球队网络原始数据

表3　CDNIM算法在足球队网络上的社团划分结果

3.4多种社团划分算法实验结果

分别利用经典的社团发现算法(GN算法[12]、K-L算法[13]、Newman快速算法[14])以及CDNIM算法对数据集进行社团划分，社团划分结果的准确率如图2所示.

3.5实验结果分析

从图2中的数据看出，CDNIM社团发现算法划分社团的正确率较高.CDNIM算法通过节点重要度矩阵来表示网络的拓扑结构，在一定程度上，节点重要度矩阵比网络的邻接矩阵更能体现节点间的相互关系.网络中的节点度值越大，那么它对邻居节点的重要度贡献比值就越大.当网络中节点之间有相互连

接时，该节点的度值发生变化，其负载和重要度也会变化，通过与邻居节点之间的传递，形成了重要度贡献关系的拓扑结构.这种网络结构表示作为划分网络社团的基准数据，能够得到更好的划分结果，准确率更高.

图2　不同的算法在5个数据集上的划分结果的准确率Fig.2　The accuracy of different algorithms on five data sets of the partition result

4结束语

本文借鉴了谱平分法的思想，将节点重要度矩阵与k-means算法相结合，提出了一种新的社团划分算法，然后利用一个聚类度量函数—模块度函数来查找出网络中最佳社团的数目，得到网络的最佳社团划分结果.CDNIM社团发现算法在多个经典的数据集上得到了正确的验证，证明了该算法在复杂网络社团发现中的有效性和正确性；通过实验发现，CDNIM社团发现算法与目前较流行的社团发现算法相比，挖掘复杂网络中的社团结构准确率较高.

参考文献

[1]Watts D J, Strogatz S H. Collective dynamics of ″small world″ networks [J]. Nature, 1998, 393(6684): 440-442.

[2]Barabási A L,Albert R Emergence of scaling in random networks[J].Science,1999,286:509-512.

[3]赵之滢，于海，朱志良，等．基于网络社团结构的节点传播影响力分析[J]．计算机学报，2014(04)：753-766．

[4]周漩，张凤鸣，李克武，等．利用重要度评价矩阵确定复杂网络关键节点[J]．物理学报，2012(05)：1-7．

[5]程泽凯，张佳玉．基于节点相似度的社团发现算法[J]．计算机工程与设计，2014(05)：1688-1693．

[6]周林，平西建，徐森，等．基于谱聚类的聚类集成算法[J]．自动化学报，2012(08)：335-1342．

[7]吴建平，宋君强，张卫民，等．计算Fiedler向量的一种高效准确方法[J]．计算机学报，2013(11)：2266-2273．

[8]罗倩．K-means聚类中心的鲁棒优化算法[J]．计算机工程与设计，2015(09)：2395-2400．

[9]沙爱晖，黄树成，李甜．一种基于网络社团结构和模块化函数的聚类算法[J]．计算机应用与软件，2014(04)：274-277．

[10]马菲，,徐汀荣，孙龙．基于三角形的重叠社团发现算法[J]．计算机应用研究，2014(02)：348-350+368．

[11]蔡晓妍，戴冠中，杨黎斌．基于谱聚类的复杂网络社团发现算法[J].计算机科学，2009(09)：49-50+95．

[12]谢锋．基于GN算法的文献聚类方法研究[J]．科技传播，2013(02):194-195．

[13]Hong Jin,Shuliang Wang,Chenyang Li. Community detection in complex networks by density-based clustering[J]. Physica A: Statistical Mechanics and Its Applications,2013(3):9219:.

[14]Amiri B, Hossain L, Crawford J W, et al. Community Detection in Complex Networks:Multi-objective Enhanced Firefly Algorithm[J]. Knowledge-Based Systems, 2013, 46(Complete):1-11.

中图分类号TP181

文献标识码A

文章编号1672-4321(2016)01-0119-04

基金项目国家自然科学基金资助项目(60473125)

作者简介吴卫江 (1971-)，男，副教授，博士，研究方向：数据挖掘，E-mail：allan1226@163.com

收稿日期2015-12-29 *通讯作者周静(1989-)，女，硕士生，研究方向：数据挖掘，E-mail：15101148869@126.com