Parameter identification for SINS coarse alignment based on apparent velocity

MENG Xiang-fei, LI Xin

(School of Electrical and Automation Engineering, Changshu Institute of Technology, Changshu 215500, China)

Parameter identification for SINS coarse alignment based on apparent velocity

MENG Xiang-fei, LI Xin

(School of Electrical and Automation Engineering, Changshu Institute of Technology, Changshu 215500, China)

Traditional dual-vector coarse alignment with apparent velocity has the problems of poor alignment precision and slow convergence rate due to the influence of random noises on inertial sensors. To solve this problem, a new dual-vector coarse alignment method is designed, which uses a new adaptive Kalman filter to estimate the parameters in an apparent velocity model without using the accurate covariance of the measurement noises. Meanwhile, a reconstructed algorithm with recognized parameters is adopted for the dual-vector, which can avoid the collinearity of the dual-vector. Analysis and simulation indicate that, by using this method, the random noises in the measured apparent velocity can be effectively eliminated compared with the traditional dual-vector coarse alignment. Simulation and turntable experiments show that, compared with traditional methods, the proposed method for the coarse alignment can acquire more accurate alignment results with the same alignment time, and can improve the convergence rate with the same alignment accuracy. The turntable tests by the new method show that the yaw error is -0.1391° and the standard deviation is 0.012°.

strapdown inertial navigation system; coarse alignment; adaptive Kalman filter; parameter identification; dual-vector attitude determination

The initial alignment is a critical technique for the strapdown inertial navigation system (SINS)[1]. The precision of the initial alignment determines the positioning precision of the pure inertial navigation. The traditional initial alignment procedure often consists of two consecutive stages: coarse alignment and fine alignment[2]. The current fine alignment methods based on Kalman filter rely heavily on the coarse alignment stage to provide a roughly known initial attitude, otherwise they cannot guarantee a rapid and accurate alignment result[3-4].

There are some coarse alignment methods such as analytical method, inertial frame method, gravitational apparent motion method and so on[5-7]. Among these methods, the dual-vector method based on the apparent velocity is an effective method for initial coarse alignment. However, because of the random noises in the apparent velocity, the performance of the coarse alignment precision was reduced, and it needs prolong alignment time to avoid the collinearity of the dual-vector.

To overcome the flaws of the traditional dual-vector coarse alignment, some methods based on low-pass filter technique are proposed[8], nevertheless, it is difficult to find an available low-pass filter for all environments with complex noise. Then, a method based on recursive least square (RLS) was proposed[9-10], the method analyzed the composition of the truth apparent velocity. With the identified parameters, the new accurate apparent velocity vector was constructed. This method can solve some existent problems in dual-vector coarse alignment. However, it needs the accurate statistical information of the sensor measurements, which can not be obtained easily from the actual system, and the error in the covariance of the measurements noises will reduce the performance of the coarse alignment.

To solve the aforementioned problems, this paper intends to adopt the new Kalman filter to estimate the parameters in the apparent velocity model[11-12]. It is based on the adaptive filter theory, so it does not need to analyze the measurement noises. And the reconstructed algorithm was used to avoid the collinearity of the dual-vector in this paper. The rest of the paper is organized as follows. The reference frame is presented in Section 1. Mechanism of the alignment method based on dual-vector is described in Section 2. Section 3 gives the adaptive Kalman filter for parameter identification and reconstruction algorithm. At last, the test results and conclusion are discussed in Section 4 and Section 5, respectively.

1 Reference frame

The coordinate frames in this paper are defined as:

1) The local level navigation frame (n): an orthogonal reference frame aligned with east-north-up (ENU) geodetic axes.

2) The SINS body frame (b): an orthogonal reference frame aligned within the IMU axes.

3) The earth frame (e): an Earth-centred Earth- fixed (ECEF) orthogonal reference frame.

4) The initial inertial frame (i0): an orthogonal reference frame non-rotating relative to the inertial frame, which is formed by the earth frame at the start-up in the inertial space.

5) The initial body frame (b0): an orthogonal reference frame non-rotating relative to the inertial frame, which is formed by the SINS body frame at the start-up in the inertial space.

2 Mechanism of the alignment method based on dual-vector attitude determination

Based on the chain-decomposition of the direction cosine matrix (DCM), the initial alignment matrix can be described as:

where, ωiedenotes the angular rate of the earth, L denotes the latitude of the IMU, and t is the alignment time.

The rate equation of IMU body frame respect to the initial IMU body frame is:

Therefore, the initial alignment can be completed with equation (1) to (9). However, there are still two problems in the aforementioned method. One is that the random noises in the apparent velocity, and the other is the collinearity of the dual-vector with the short time intervals, these contaminate the alignment results. To avoid the two problems, the adaptive Kalman filter technique was proposed in the next section.

3 Adaptive Kalman filter for parameter identifycation and reconstruction algorithm

To acquire more accurate alignment results compared with the existing methods, a novel method based on the parameter identification is proposed in the next subsection. With the estimated parameters, the new dual-vector can be reconstructed, and the two aforementioned problems can be eliminated effectively.

3.1 Parameter identification model

From the dual-vector coarse alignment, the critical step is how to calculate the apparent velocityb0, which can be obtained by integrating the apparent gravity gb0, it is calculated as:

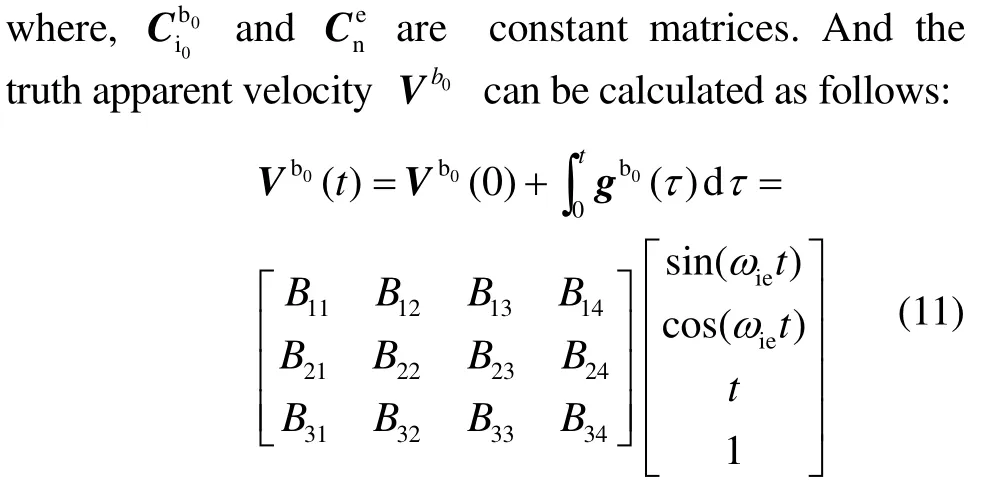
where, B is the parameter matrix which used to construct the apparent velocity, and it is more accurately over the alignment time.

3.2 Adaptive Kalman filter

The RLS method can be used to estimate the parameter matrix, however, it needs the accurate measurement covariance, which cannot be attained easily from the actual system. In this paper, a new Kalman filter is used to estimate the parameters, which is an adaptive filter, so it does not need the accurate statistics of the noises of the measurements. To develop the adaptive Kalman filter, the filter model is constructed, firstly.

1) Filter model

The filter model on the z-axis is given as:

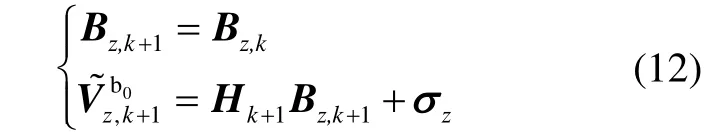
where, Bzdenotes the third line of the parameter matrix,denotes the z-axis element of thewhich can be obtained by equation (5), and σzis the random noise.

2) Adaptive Kalman filter

Adopting to the filter model, the adaptive Kalman filter for parameter identification can be described as:

where, i=x,y,z, ei,kdenotes the i-axis residual error, and Λi,k+1is the i-axis adaptive parameter.

3.3 Reconstruction algorithm

With the adaptive Kalman filter, the parameter matrix B can be obtained accurately over the alignment time, then the new apparent velocity can be obtained by equation (11). To avoid the collinearity ofthe dual-vector, the traditional method needs to prolong the alignment time, because the interval of t1and t2is the decisive factor. To overcome the flaws of the traditional method, with the equation (11), the reconstructed dualvector can be obtained as:

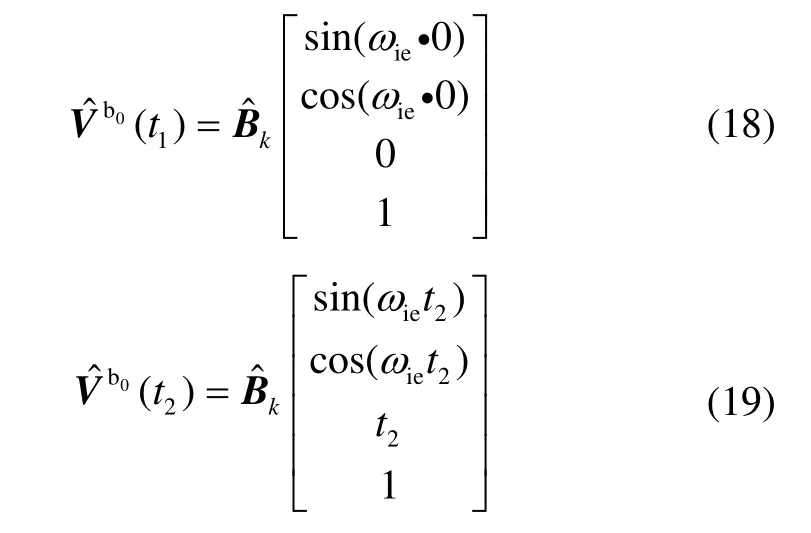
where, t1is always the initial time, so compared with the traditional method where t1is equal to t2/2, the new method has longer interval, and it can avoid the collinear problems effectively.

4 Test results

In order to validate the effectiveness of the coarse alignment method presented in this paper. The simulation and the turntable tests were carried out, and the comparative results with the existing method are given in the next subsection.

4.1 Simulation test

In order to analyze the real alignment results, we design the swaying alignment test to simulate the static ship. The swaying parameters are listed in Tab.1, the inertial sensors parameters are shown in Tab.2, and the initial values of the adaptive Kalman filter are listed in Tab.3.

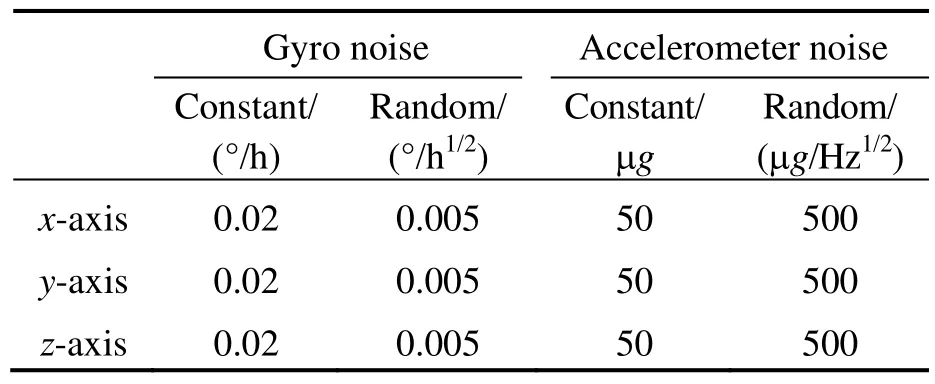
In the simulation test, the update frequency for sensor outputs and alignment solution are both set as 200 Hz, while the statistic frequency for the alignment errors is 2 Hz. After the simulation of 600 s, the apparent velocity errors and the alignment errors are shown in Fig.1 and Fig.2, respectively, and the statistic results are listed in Tab.4.

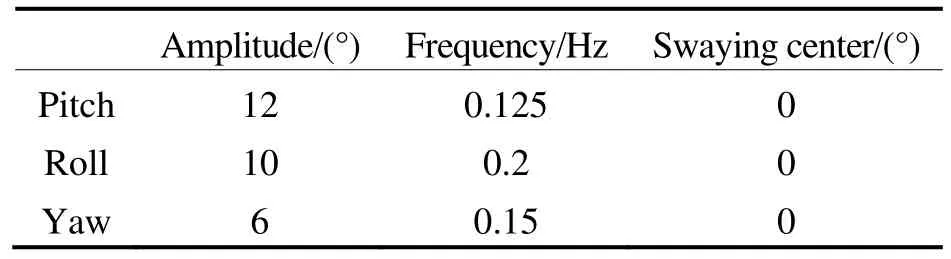
Tab.1 Setting of swinging parameters

Tab.2 Setting of sensor errors

Tab.3 Initial value of adaptive Kalman filter

In Fig.1, the random noises of the apparent velocity are smoothed, with the advantages of the adaptive Kalman filter, the apparent velocity can be obtained accurately, which determines the alignment precision by equation (9). In Fig.2, the alignment errors show that the proposed method obtains the more smoothed results, and the random noises still influence the results of the traditional dual-vector coarse alignment, it also can be founded that the RLS method gives the sub-optimal alignment results. As can be seen in Tab.4, the errors of pitch and roll are close by comparing with the three methods. However, the yaw alignment errors are smaller than the existing method, and with the standard deviations, the proposed method is smaller than the others in the same instant time of the whole alignment. This means the proposed method has more effective performance in yaw alignment errors, and the convergence rate is faster.

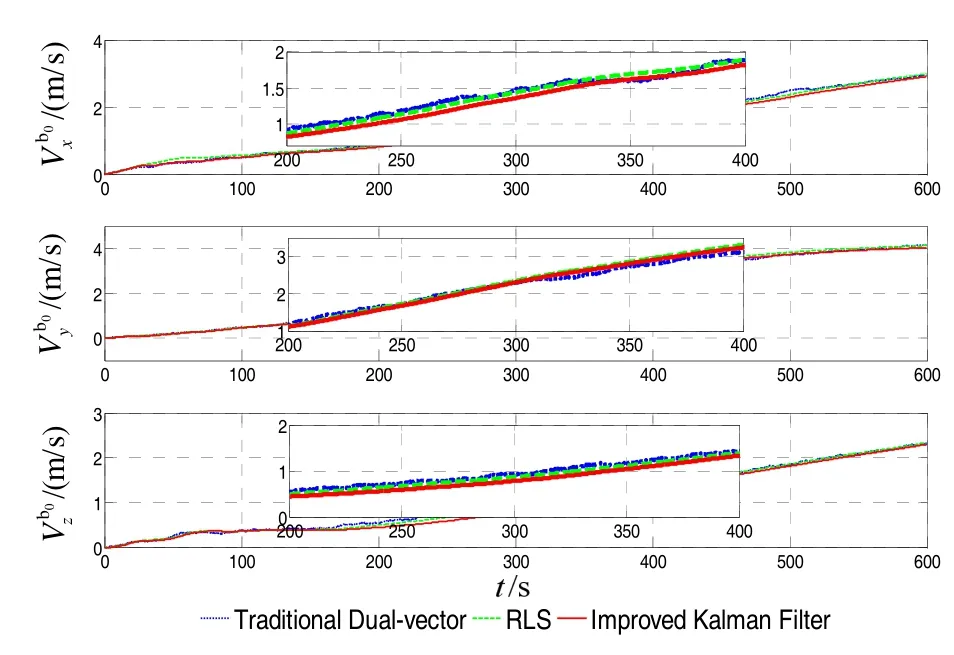
Fig.1 Errors of apparent velocities

Fig.2 Curves of alignment errors

Tab.4 Statistics of alignment errors (°)

4.2 Turntable test

The turntable test is carried out to confirm the proposed methods in the real-time initial alignment. The swaying parameters is set the same as the simulation test (see Tab.1), and the IMU is installed as Fig.3

Fig.3 Turntable and IMU

The alignment results and the statistical information of the alignment errors are shown in Fig.4 and Tab.5, respectively.

In Fig.4, we can find out that there is oscillation in the alignment errors, which matches the real results, and the alignment precision in pitch and roll is close. However, the proposed method has higher performance in yaw.

As amplified figure in Fig.4 and the statistics in Tab.5, the improved Kalman filter method has more smooth results in alignment errors. During the whole alignment process, the means of pitch and roll errors are very close, while the standard deviations of the improved Kalman filter method are slightly smaller than the traditional dual-vector and RLS method. In addition, the means of yaw of the improved Kalman filter method are approximately close to the RLS method, but the deviations of the proposed method are greatly smaller than the other two methods.

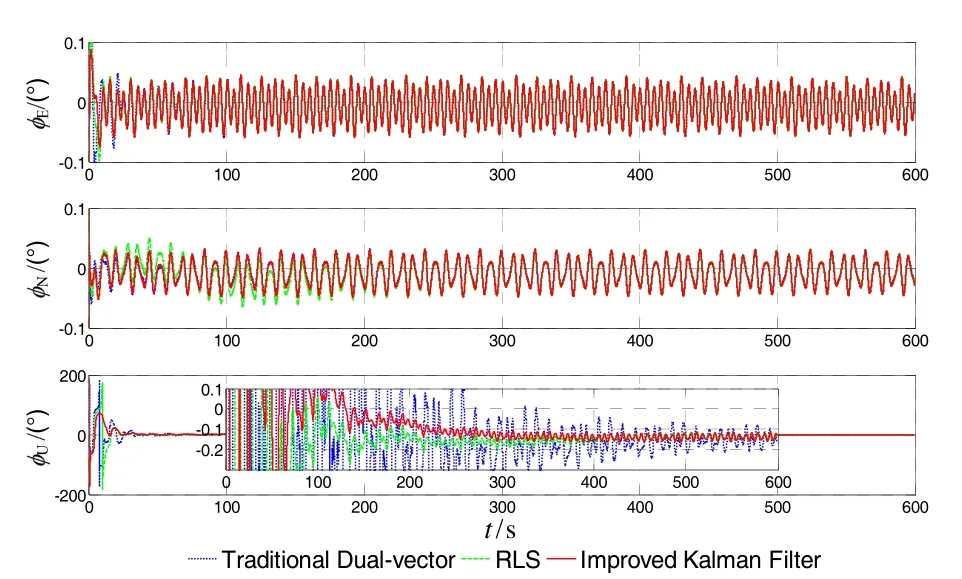
Fig.4 Alignment errors in turntable test

Thus, the conclusion can be obtained: the proposed alignment method with parameter identification and reconstruction can increase alignment accuracy without adding alignment time.

Tab.5 Statistic of alignment errors in turntable test (°)

5 Conclusion

In this paper, a new dual-vector coarse alignment method based on the apparent velocity has been proposed, which adopts the adaptive Kalman filter for parameter identification, and use the effective reconstructed dual-vector to eliminate the two problems in the traditional dual-vector coarse alignment.

Simulation and turntable tests are designed in this thesis, the results indicates that compared with the existing method, the adaptive Kalman filter method has higher performance of the coarse alignment, it mainly shows in alignment accuracy and convergence rate.

[1] Titterton D, Weston J L. Strapdown inertial navigation technology[M]. United Kingdom: Institution of Electrical Engineers, 2004.

[2] Wang Xin-long. Initial alignment for strapdown inertial navigation system on moving and static base[M]. Northwestern Polytechnical University Press Ltd, 2013.

[3] Silson P M G. Coarse alignment of a ship’s strapdown inertial attitude reference system using velocity loci[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(6): 1930-1941.

[4] Li J, Xu J, Chang L, et al. An improved optimal method for initial alignment[J]. Journal of Navigation, 2014, 67(4): 727-736.

[5] Lian J, Tang Y, Wu M, et al. Study on SINS alignment algorithm with inertial frame for swaying bases[J]. Journal of National University of Defense Technology, 2007, 29(5): 95-99.

[6] Qin Yong-yuan, Yan Gong-min, Gu Dong-qing, et al. A clever way of SINS coarse alignment despite rocking ship[J]. Journal of Northwestern Polytechnical University, 2005, 23(5): 681-684.

[7] Li Q, Ben Y, Sun F. A novel algorithm for marine strapdown gyrocompass based on digital filter[J]. Measurement, 2013, 46(1): 563-571.

[8] He Hong-yang, Xu Jiang-ning, Li Jing-shu, et al. Improved fast backtracking alignment approach for strapdown inertial navigation system[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 179-183.

[9] Liu X, Zhao Y, Liu X, et al. An improved self-alignment method for strapdown inertial navigation system based on gravitational apparent motion and dual-vector[J]. Review of Scientific Instruments, 2014, 85(12): 125108.1-125108.11.

[10] Liu X, Zhao Y, Liu Z, et al. A novel self-alignment method for SINS based on parameter recognition and dual-velocity vectors[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(12): 0954410014568798.

[11] Panuska V. A new form of the extended Kalman filter for parameter estimation in linear systems with correlated noise[J]. IEEE Transactions on Automatic Control, 1980, 25(2): 229-235.

[12] Qin Fang-jun, Li An, Xu Jiang-ning. Improved fast alignment method of strapdown INS using bidirectional processes and denoising[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 453-458.

基于参数识别视速度的双矢量粗对准方法

孟翔飞，李 鑫
（常熟理工学院 电气与自动化工程学院，常熟 215500）

针对传统基于视速度双矢量粗对准中，由于传感器随机噪声的影响，存在对准精度差，收敛速度慢的缺点，提出了一种新型自适应 Kalman滤波的参数识别粗对准方法。该方法通过对视速度运动进行建模，设计采用自适应Kalman滤波对模型参数进行参数识别，从而有效地消除视运动中的随机噪声，提高粗对准的精度和收敛速度。由于自适应滤波的特点，新方法不需要对传感器误差进行统计，使其在实际系统中具有更加广泛的应用价值。针对双矢量粗对准的计算特点，设计了一种矢量重构算法，从而尽可能地规避双矢量共线性问题，加快了粗对准的收敛过程。仿真与转台实验表明，与传统方法对比，新方法在相同的对准时间内具有更高的对准精度，在相同的对准精度下，具有更高的收敛速度。转台实验的最终对准精度为-0.1391°，标准差为0.012°。

捷联惯导系统；粗对准；改良Kalman滤波；参数辨识；双矢量姿态确定

U666.1

：A

2016-09-02；

：2016-11-20

江苏省产学研联合创新资金（BY2014075）；江苏高校品牌专业建设工程资助项目（PPZY2015C215）

孟翔飞（1977—），男，副教授，博士，从事导航定位研究。E-mail: mxf0316@163.com

1005-6734(2016)06-0730-06

10.13695/j.cnki.12-1222/o3.2016.06.006