旋转加速度计式重力梯度仪输出解调与滤波

杨 晔，李 达，高 巍

（天津航海仪器研究所，天津 300131）

旋转加速度计式重力梯度仪输出解调与滤波

杨 晔，李 达，高 巍

（天津航海仪器研究所，天津 300131）

重力梯度仪是对地球表面微小重力梯度变化进行连续测量的仪器。由于核心敏感元件加速度计工艺与性能水平限制，以及多环节安装误差等因素导致系统实际输出信号中包含了大量噪声，且信噪比极低，为了能够在强噪声中有效提取真实的重力梯度信号，需在信号解调过程中降低谐波干扰引起的测量偏差。结合误差产生机理，分析比较了不同的解调方法对重力梯度信号解调的影响，明确了合理的信号解调手段。同时，在数据处理过程中增加带通滤波环节，进一步降低动态噪声对系统的影响。结合动态摇摆实验数据的仿真验证结果表明：上述措施对重力梯度仪原始观测数据的噪声抑制具有明显效果，测量偏差在一定程度上得到解决，解调后信号的噪声幅度下降至20%，提高了系统的空间分辨率，具有工程化应用意义。

重力梯度仪；信号提取；带通滤波；同步解调

重力梯度仪是用于测量重力场分布梯度的精密设备，基于Bell Aerospace公司提出的旋转加速度计测量原理的重力梯度仪（后文中简称梯度仪）是迄今唯一实用的近地表动态测量重力梯度仪[1-3]。碍于重力梯度信号的微弱和加速度计性能的限制，梯度仪输出信号的信噪比极低，需后期数据处理进一步提高测量精度[4-6]。由于世界范围内能够从事该技术研究的国家和单位很少，相关技术文献鲜有报道，本文结合科研工作和实测数据来验证方法的有效性，优化重力梯度信号数据处理过程。

1 重力梯度测量原理与存在问题

1.1 测量原理

如图1所示，旋转加速度计式重力梯度仪基于加速度计位置差分测量原理，通过机械旋转的方式将重力梯度张量分量调制到系统旋转频率的二倍频处。加速度计输出与重力梯度张量分量之间的关系可表示为

式中：a1、a2、a3、a4是4个加速度计的输出；R是加速度计检测质心到旋转中心的距离，Γxx、Γyy、Γxy是重力梯度张量分量；ω是旋转装置的旋转角速度。

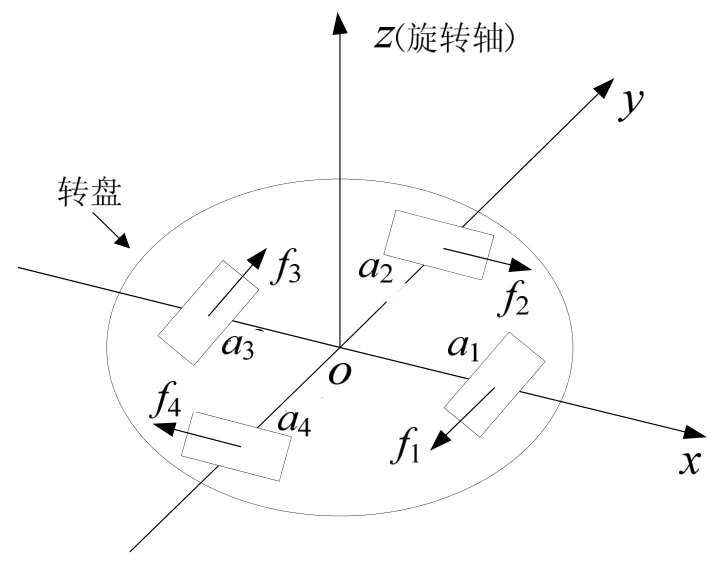
图1 旋转加速度计式重力梯度仪测量原理Fig.1 Measurement principle of rotating accelerometer gravity gradiometer

以往的信号解调方案如图2所示，其中方波解调公式为

式中：Aout(i)是经位置同步的加速度计输出采样值；N是重力梯度仪圆盘旋转半周时采样数据个数；R是旋转半径；π2是将解调值转化为幅值的比例系数。

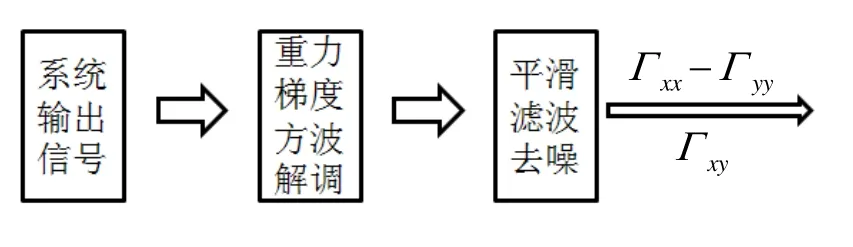
图2 原始重力梯度数据处理框图Fig.2 Flow chart for processing the original gravity gradiometer data

1.2 存在问题

梯度仪在进行水平摇摆试验（摇摆幅度为2°，摇摆周期为20 s）时的典型解调出的信号如图3所示，可以看出在4 892 s由静态开始摇摆时，信号均值出现600E(1E=10-9s-2)的偏差“台阶”，并且原始信号信噪比极低，噪声峰峰值高达10000E，相关数据见表1。

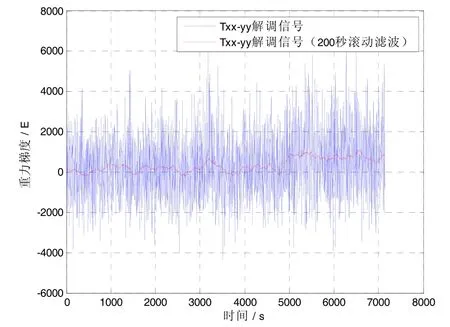
图3 摇摆试验时梯度仪Γxx-Γyy解调信号（方波解调）Fig.3 Demodulation signal of gravity gradiometer Γxx-Γyyin swing test (square-wave demodulation)

表1 摇摆试验梯度信号Γxx-Γyy的均值和标准差(方波解调)Tab.1 Mean values and standard deviations of gravity gradient signals in swing test (square-wave demodulation)

2 梯度仪数据处理方法

在此分析梯度仪在摇摆试验中出现的测量偏差的机理，系统可采用的解调方式主要有方波解调和正弦解调两种，其中正弦解调的公式为

式中：ts是梯度仪的采样时间间隔；分子上的2是将解调值转化为幅值的比例系数。两种解调方式在解调2ω频率上的信号幅频响应对比如图4所示。

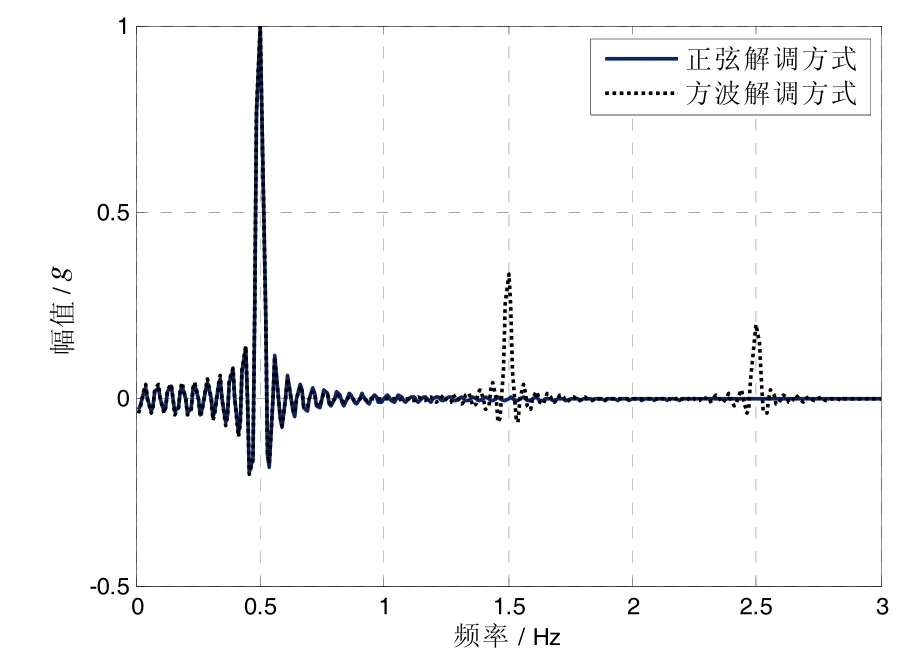
图4 方波解调和正弦解调方式幅频响应对比Fig.4 Comparison on amplitude-frequency responses between square-wave demodulation and sinusoidal demodulation

从图4可以看出，在解调频点附近，两种解调方式效果相当，但在解调频率的奇数倍频处，方波解调方式会引入高频谐波项，而正弦解调方式的结果不被高频谐波项影响。引入一个模拟梯度信号y= sin(2πf1t)+sin(2πf2t )进行仿真验证（其中，f1=2ω，f2=6ω），该信号时域图见图5（T=12ω），解调结果对比见表2。

图5 模拟梯度信号时域图Fig.5 Time domain of simulated gravity gradiometer signal

表2 两种解调方式模拟梯度信号解调结果对比Tab.2 Comparison of two demodulation methods for simulated gradient signals

由此可知，方波解调值会以一定比例引入高频谐波分量，由于摇摆试验中在机械旋转调制频率的高频谐波频点处存在较大噪声耦合，方波解调的方式会将这些谐波频点噪声转化为解调值，汇入梯度信号，导致梯度信号出现测量偏差，而正弦解调值不会受到高频谐波噪声的影响。从图4可以看出，解调频点附近的噪声也会对解调结果产生影响，如果原始数据存在频率差为Δf，幅值为A的噪声项，其对解调值的影响为

式中：k为解调值序号。由式(5)可得解调频点附近的噪声会使解调结果出现等幅的余弦震荡，增加梯度信号噪声，因此需在解调前加入带通滤波环节以提高解调精度。并且由式(4)可知，频率差为Δf噪声项会引起解调结果呈周期为1(2Δf)的余弦振荡，因此解调后对梯度信号低通滤波器截止频率的选择与原始信号带通滤波器的带宽参数息息相关。如果带通滤波器的带宽参数为f，解调后对梯度信号的低通滤波器截止频率必须低于f才有降噪效果。在实际工作中可结合梯度仪自身性能和外部环境噪声水平综合考虑是否对梯度信号进行低通滤波。

3 实验数据处理与结果分析

将同样的摇摆试验数据进行正弦解调，梯度信号如图6所示，相关数据见表3，从中可以看出，梯度信号在水平摇摆试验时的测量偏差可在一定程度上得到解决，偏差幅度从600 E降至20 E。

图6 摇摆试验梯度仪Γxx-Γyy解调信号(正弦解调）Fig.6 Demodulation signal of gravity gradiometer Γxx-Γyyin swing test (sinusoidal demodulation)

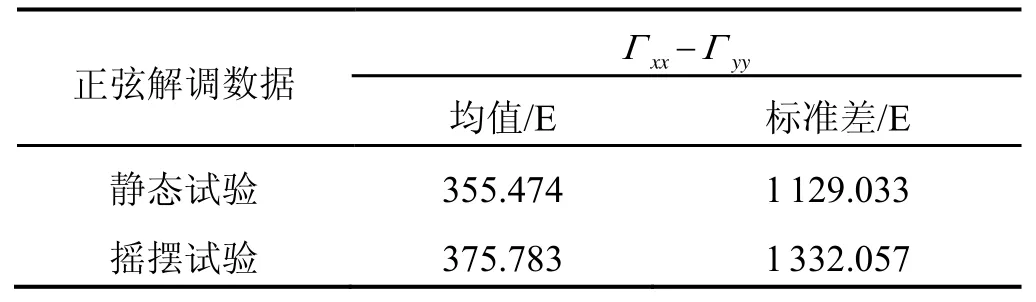
表3 摇摆试验梯度信号Γxx-Γyy的均值和标准差(正弦解调)Tab.3 Mean values and standard deviations of gravity gradient signals in swing test (sinusoidal demodulation)

为进一步验证正弦解调方式的合理性，分别将两种解调方式的解调值与原始数据在2ω(Hz)处的FFT（快速傅式变换）值作比较，其结果见表4。从表4中可以看出，方波解调得到的梯度信号与原始数据在2ω(Hz)处的FFT值相差较大，是由于引入的高频谐波噪声耦合项不稳定导致的，而正弦解调的信号与FFT值一致，因此使用正弦解调方式得到的梯度信号更加接近真实值。

再在解调前对原始数据增加带通滤波环节，根据梯度仪输出信号特征并在考虑仪器测量信息空间分辨率的基础上，在采样频率800 Hz的条件下设计一组合理的带通滤波器参数：中心频率为2ω(Hz)，窗口函数为凯塞窗，带通带宽为0.01 Hz，过渡带带宽为0.005 Hz，滤波器阶数为64 000。将滤波后数据解调得到梯度信号如图7所示，相关数据见表5。可见带通滤波后梯度信号降噪效果明显，梯度信号噪声峰峰值降为1000E左右，标准差降为原来的20%左右。

表4 摇摆试验梯度仪输出信号两种解调方式在2ω(Hz)处FFT值对比Tab.4 Comparison on FFT values of gradient signals at 2ω(Hz) by the two demodulation modes in swing test

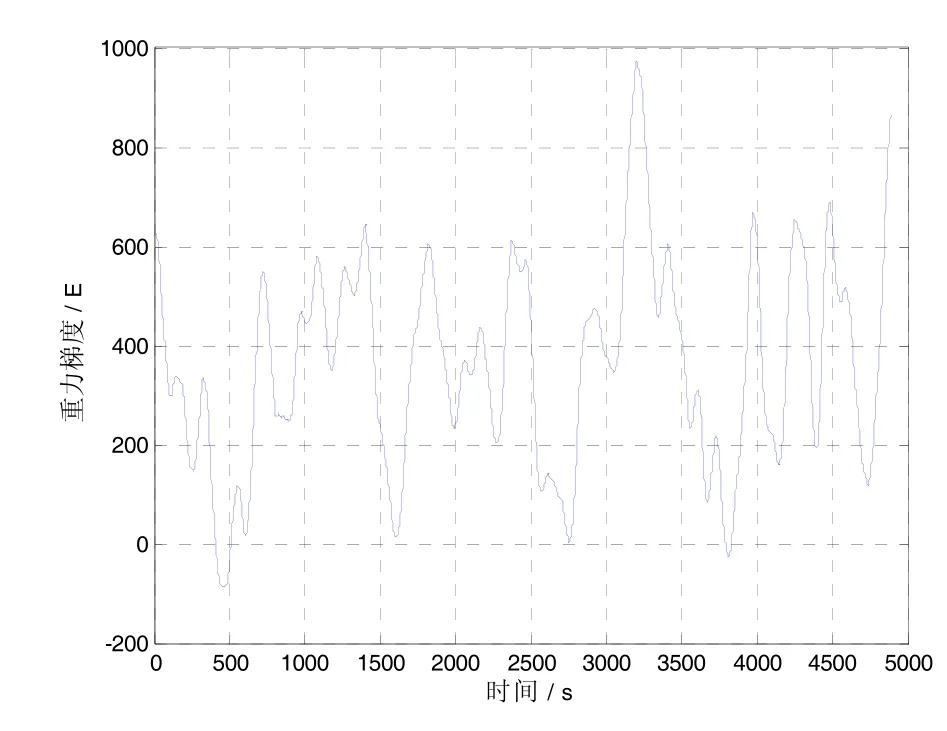
图7 带通滤波后梯度张量Γxx-Γyy解调信号Fig.7 Band-pass filtered gravity gradient tensor Γxx-Γyydemodulation signal

表5 使用带通滤波器后解调效果对比(未平滑处理)Tab.5 Comparison on demodulation effects after band-pass filtering (no smoothing)

在梯度仪实际工作中，即使在解调前增加带通滤波环节，梯度信号噪声仍然很大，仍需对其进行平滑滤波处理。将通过带通滤波器后解调得到的梯度信号与原始梯度信号分别使用 N秒平滑滤波并计算标准差，对比结果如图8所示，相关数据见表6。

从图8中可以看出，在使用带通滤波处理后对解调出来的梯度信号使用100 s以下的平滑滤波处理，其对噪声的抑制效果不明显，如需进一步降噪需进行更长时间的平滑滤波处理，这是由于带通滤波器的通带带宽参数为0.01 Hz造成的。从表6中还可以看出，仅使用带通滤波处理后，解调的梯度信号均值会发生幅值为4E的数据偏移现象，但再经过平滑滤波后偏移现象消失，这是由于在2ω(Hz)上存在信号串扰，这里可以对梯度信号使用平滑滤波的手段消除。

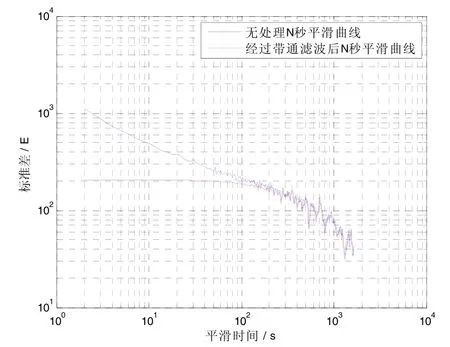
图8 梯度信号N秒平滑曲线对比Fig.8 Comparison on curves of gradient signals before and after smoothing for N seconds

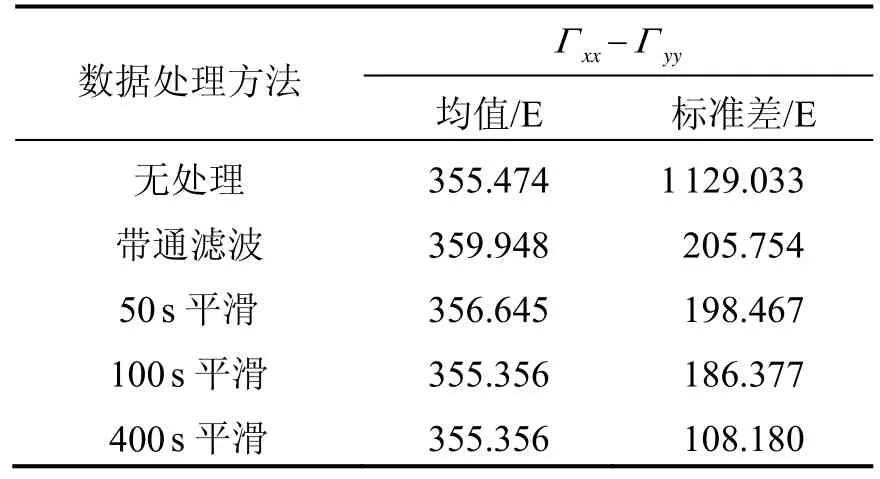
表6 重力梯度不同数据处理方法结果对比Tab.6 Comparison on different data processing methods for gravity gradient data

改进后的重力梯度信号数据处理过程如图 9所示。通过增加带通滤波环节的手段可将梯度信号噪声降至原来的20%左右，达到提高梯度仪测量信息空间分辨率的目的。将解调方式改为正弦解调可以有效地消除测量偏差，提高仪器测量分辨率。

图9 改进后重力梯度数据处理框图Fig.9 Flow chart for processing the improved gravity gradiometer data

4 总 结

本文针对梯度仪输出信号特征，提出一种重力梯度信号提取的有效方法：

1）使用带通滤波器对梯度仪原始输出信号进行滤波，可将重力梯度信号频点外的干扰噪声滤掉；

2）对滤波后的信号用正弦解调代替方波解调，以消除谐波频点处的噪声引起的测量偏差；

3）将解调后的梯度信号进行平滑滤波处理，进一步来提高测量分辨率。

通过采用上述方法对梯度仪原始测量数据进行离线处理，测量偏差可在一定程度上得到解决，同时信号噪声标准差可有效降低到原来的20%，噪声峰峰值降低到1000E，提高了梯度仪的测量精度和测量信息的空间分辨率，为实现高精度动态重力梯度测量提供了一种数据处理的方法。

（References）：

[1] Roberts D R, Chowdhury P J, Lowe S, et al. Airborne gravity gradiometer surveying of petroleum systems under Lake Tanganyika, Tanzania[C]//ASEG-PESA2015. 2015: 1-4.

[2] DiFrancesco D, Meyer T, Christensen A, et al. Gravity gradiometry—today and tomorrow[C]//11thSAGA Biennial Technical Meeting and Exhibition. Swaziland, 2009: 80-83.

[3] Dransfield M H, Christensen A N. Performance of airbornegravity gadiometers[J]. The Leading Edge, 2013, 32(8): 908-922.

[4] Lee J B. FALCON gravity gradiometer technology[J]. Exploration Geophysics, 2001, 32(4): 247-250.

[5] Christensen A N, Dransfield M H, Galder C V. Noise and repeatability of airborne gravity gradiometry[J]. First Break, 2015, 33: 55-63.

[6] 蔡体菁, 钱学武, 丁昊. 旋转加速度计重力梯度仪重力梯度信号仿真[J]. 物探与化探, 2015, 39(S1): 76-79. Cai Ti-jing, Qian Xue-wu, Ding Hao. Signal simulation of gravity gradiometer of rotating accelerometer[J]. Geophysical and Geochemical Exploration, 2015, 39(S1): 76-79.

[7] 刘昱, 张宇, 潘军, 等. 重力梯度测量中光栅角编码器安装误差的影响及分析[J]. 中国惯性技术学报, 2015, 23(1): 6-8. Liu Yu, Zhang Yu, Pan Jun, et al. Influence and analysis of optical angular encoder’s installation error in gravity gradiometry[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 6-8.

[8] O’keefe G J, Lee J B, Turner R J, et al. Gravity gradiometer. US: No.5922951[P]. 1999-10-05.

[9] Van Leeuwen E H, McCracken K G, Lee J B. Airborne gravity gradiometers. US: No.6883372 B2[P]. 2005.

[10] 钱学武, 蔡体菁, 尹航. 一种旋转加速度计重力梯度仪重力梯度解调方法[J]. 物探与化探, 2015, 39(S1): 80-83. Qian Xue-wu, Cai Ti-jing, Yin Hang. A gravity gradient demodulation method for rotation accelerometer gravity gradiometer[J]. Geophysical and Geochemical Exploration, 2015, 39(S1): 80-83.

[11] Moody M V, Paik H J. A superconducting gravity gradiometer for inertial navigation[C]//2004 IEEE Position Location and Navigation Symposium. 2004: 775-781.

[12] 钱学武, 蔡体菁. 旋转加速度计重力梯度仪加速度计标度因数实时反馈调整方法[J]. 中国惯性技术学报, 2016, 24(2): 148-153. Qian Xue-wu, Cai Ti-jing. Real-time feedback adjusting methods for accelerometer scale factor in gravity gradiometer for rotating accelerometer[J]. Journal of Chinese Inertial Technology, 2016, 24(2): 148-153.

Gradient signal demodulation and filtering for rotating accelerometer gravity gradiometer

YANG Ye, LI Da, GAO Wei
(Tianjin Navigation Instrument Research Institute, Tianjin 200131, China)

In rotating accelerometer gravity gradiometer, due to the limitation of the accelerometer’s process and performance level and the effects of various installation errors, there are lots of noises in the system output signal, and the SNRs are extremely low. In order to effectively extract the real gravity gradient signals in strong noises, the measurement errors caused by harmonic interference must be reduced in the process of signal demodulation. Combined with the error generation mechanism, the influences of different demodulation methods on the gravity gradient signal demodulation are analyzed and compared, and a reasonable method of signal demodulation is chosen. Meanwhile, a band-pass filter is added in the data processing process to further reduce the influence of the dynamic noise. Combined with dynamic swing test data, the simulations show that the above measures have obvious effect on the noise suppression of the original gravity data, and the noise amplitude of the demodulated signal is reduced to 20%, which improves the spatial resolution of the system, and has the engineering application value.

gravity gradiometer instrument; signal extraction; band-pass filter; synchronous demodulation

U666.1

：A

2016-10-02；

：2016-11-20

国家高技术研究发展计划（863计划）（2011AA060501）；总装预研项目（51309040702）

杨晔（1968—），男，研究员，硕士生导师，从事导航、制导与控制方面研究工作。E-mail: Liuyuyangye@eyou.com

1005-6734(2016)06-0701-05

10.13695/j.cnki.12-1222/o3.2016.06.001