机抖激光陀螺敏感轴动态偏移误差参数估计与补偿
王 林,吴文启,潘献飞,李 耿
(1. 国防科学技术大学 机电工程与自动化学院,长沙 410073;2. 国防科学技术大学 光电科学与工程学院,长沙 410073)
机抖激光陀螺敏感轴动态偏移误差参数估计与补偿
王 林1,吴文启1,潘献飞1,李 耿2
(1. 国防科学技术大学 机电工程与自动化学院,长沙 410073;2. 国防科学技术大学 光电科学与工程学院,长沙 410073)
针对振动环境下机抖激光陀螺敏感轴产生动态偏移造成惯导系统精度下降的问题,从理论上推导了机抖激光陀螺敏感轴动态偏移误差模型,并结合工程实际建立了简化的误差模型;在此简化误差模型基础上,推导了陀螺敏感轴动态偏移造成的等效陀螺漂移与比力、角速度的耦合关系;将机抖激光陀螺敏感轴动态偏移误差归结为9个待辨识参数,针对该模型中的待辨识参数设计了标定方法,并给出了标定实验设计原则;以姿态误差为观测量进行振动实验对待辨识参数进行估计,振动实验结果表明,在10 min线振动时间内,机抖激光陀螺敏感轴动态偏移误差补偿后,捷联惯导系统纯惯导速度误差减小30%以上。
机抖激光陀螺;敏感轴动态偏移;误差模型;参数标定
机抖激光陀螺以其特有的优势在捷联式惯性导航系统中得到了广泛应用。捷联式惯性导航系统由于与载体直接固联,惯性器件直接敏感载体的运动,因此对惯性器件的性能提出了更高的要求。
影响捷联式惯导系统导航精度的原因很多,除了安装误差、标度因数误差、惯性器件的零位误差外,运载体线振动、角振动造成的动态误差也是很重要的因素。为了减小振动对机抖激光陀螺捷联惯导系统的影响,需要合理设计减振结构[1-4]。在充分减振的基础上,振动环境下惯导系统的精度仍迅速下降,产生了明显的姿态漂移,即使将姿态解算频率提高到 4000 Hz,导航误差仍然没有得到改善。文献[5]中对俄罗斯Cyclone 4运载火箭的机抖激光陀螺捷联惯导系统的随机振动试验测试也表明,振动环境下,激光陀螺可能存在与高频振动分量相关的误差。由于机抖激光陀螺存在活动部件抖轮[6],加速度作用下抖动轴弯曲,形成等效安装偏差,进而产生等效陀螺漂移。
针对这种情况,文献[7-9]重新设计了机抖激光陀螺抖轮的结构,使得单表级激光陀螺在振动环境下的精度有了明显改善,但是没有给出振动环境下系统级精度测试情况。文献[10]理论推导了由机抖激光陀螺抖动轴弯曲变形造成的漂移误差,认为该误差与输入加速度及载体的动态频率成正比,并进行了仿真验证,但没有进一步的实验验证和误差补偿方法。目前公开的文献很少有关于机抖激光陀螺敏感轴动态偏移误差模型的解析分析及其误差参数标定方案。
本文建立了机抖激光陀螺敏感轴动态偏移的理论模型,分析其误差机理,并设计了相关误差参数的标定方法,最后给出了初步的误差补偿实验结果。
1 机抖激光陀螺敏感轴动态偏移误差模型
设机抖激光陀螺捷联惯导系统IMU的x陀螺敏感轴为x轴,y陀螺敏感轴为y轴,z陀螺敏感轴为z轴;设εxy、εxz分别为x陀螺敏感轴绕y轴、z轴转动的形变角;εyx、εyz分别为y陀螺敏感轴绕x轴、z轴转动的形变角;εzx、εzy分别为z陀螺敏感轴绕x轴、y轴转动的形变角。无外部力学环境作用下,以x陀螺敏感轴为基准,εyz0为y陀螺敏感轴绕z轴转动的常值偏角;εzx0、εzy0分别为z陀螺敏感轴绕x轴、y轴转动的常值偏角,则动态情况下敏感轴动态偏移造成的等效陀螺漂移误差模型可表示为

式中:第一项为陀螺敏感轴常值偏角、动态偏移形变角对应的等效安装偏差造成的动态误差,第二项为陀螺敏感轴动态偏移形变角对应的等效圆锥误差。
陀螺敏感轴动态偏移形变角满足以下动力学方程:

式中:Jx=Jy=Jz=J为x陀螺、y陀螺、z陀螺绕其各自敏感轴方向的转动惯量;
Jxy≈Jxz≈Jyx≈Jyz≈Jzx≈Jzy≈J1为x陀螺、y陀螺、z陀螺绕与其敏感轴正交的对称轴的转动惯量;
cxy≈cxz≈cyx≈cyz≈czx≈czy≈c 为陀螺抖轮的侧向形变阻尼;
kxy、kxz、kyx、kyz、kzx、kzy分别为各个陀螺抖轮的侧向刚度,m为陀螺光学本体的质量;
[lxxlxylxz]T、[lyxlyylyz]T、[lzxlzylzz]T分别为x陀螺、y陀螺、z陀螺质心偏离的杆臂参数;
ωdx、ωdy、ωdz分别为x陀螺、y陀螺、z陀螺的抖动角速率。
同一陀螺不同方向的侧向刚度非常接近,可以忽略非等弹性的影响,即:

为便于实际工程应用,对式(2)进行简化,以x陀螺为例进行说明。考虑到x陀螺沿y、z方向形变阻尼的影响,忽略交叉耦合项的影响,同时忽略、的影响(其影响等价于动力学方程的外界输入),只考虑偏心力矩对 x陀螺敏感轴侧向形变的影响。x陀螺的动力学方程可以简化为

假设作用到x陀螺上的等效偏心力矩为正弦力矩Mcos(ωt),由于减振器对高频振动的隔离,实际作用于陀螺的偏心力矩的频谱集中于低频段。鉴于陀螺敏感轴侧向形变的固有频率一般在700 Hz以上[10],则有:


同理,可得y、z陀螺侧向形变的稳态响应近似解。式(2)所示动力学方程的稳态响应近似解为

考虑到式(1)中陀螺敏感轴常值偏角是陀螺安装参数的一部分,可以通过标定消除。忽略非等弹性影响时,陀螺敏感轴动态偏移形变角对应的等效圆锥误差也很小,可以忽略。进一步根据式(7),将式(1)简化为

式(8)即待分析评估的结合机抖激光陀螺敏感轴偏移形变的动态误差补偿简化模型,包含9个待辨识的参数。根据该式,在复杂线振动、角振动环境下,会耦合出等效陀螺漂移误差,造成姿态误差,进而造成速度、位置误差。
2 误差参数标定
在固定位置处,静止一段时间后,继而对惯导系统施以固定频率线振动。机抖激光陀螺敏感轴偏移形变会产生等效陀螺漂移,相对地理系造成的姿态误差微分方程表示为
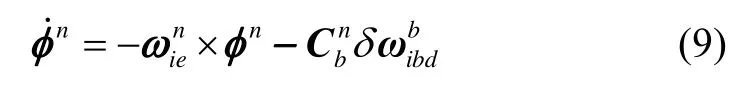
记时刻t0为线振动开始时刻,振动持续时间记为T,则t0+T时刻的姿态误差为

考虑到式(11)右侧包含φn(t)项,采用递推数值积分获得式(11)的数值解,该数值解表示为τ的函数形式。忽略对准造成的姿态误差,即时刻t0的姿态误差记为φn(t0)=0。t0+T时刻线振动结束,惯导静止一段时间进行对准,利用此姿态基准获得t+T时刻的姿态误差观测值:

根据式(11)、(13),设计多组线振动实验,利用最小二乘法实现九个误差参数的标定。
3 实验设计及初步的结果
标定过程需要充分激励误差,不同振动实验条件下,可以对不同的待辨识参数造成的误差进行充分激励。从式(8)可以看出,比力与角速率乘积项耦合,产生等效漂移。据此,可以设计线振动实验对待辨识参数进行标定估计。
线振动实验设计:为了使得惯导系统在线振动条件下同时存在较大的角运动,需要在惯导系统安装底座的下部加装外减振器,之后将系统固联到振动台上;通过调整工装,分别使得惯导系统的X、Y、Z轴冲天,进而分别沿惯导系统的两个水平轴方向、对角线方向进行固定频率线振动实验(图 1所示),这样便实现了陀螺在各个方向误差参数的充分激励。

图1 线振动实验示意图Fig.1 Sketch of the linear vibration experiment
在振幅为2g,频率为20 Hz正弦线振动条件下,按照误差模型和标定方法对某90型机抖激光陀螺捷联惯导系统(图2所示)待辨识参数进行标定,得到未知参数值。每组振动实验按照以下顺序组织:惯导系统首先静止10 min,然后振动10 min,最后再次静止10 min。考虑到t0+T时刻的姿态参考矩阵的航向角误差受等效东向陀螺漂移的影响较大,t0+T时刻的姿态误差参考值只取水平姿态角误差。

图2 线振动实验Fig.2 Linear vibration experiment
在补偿掉加速度计尺寸效应和二次平方项误差的基础上,将辨识得到的参数用于振幅为 2g,频率为40 Hz的正弦线振动实验误差补偿,验证误差模型的补偿效果。图3给出了相应时间段内水平方向加速度、角速率乘积项的积分曲线图4给出了补偿前后速度误差对比曲线。

图3 积分曲线Fig.3 Integral curve

图4 初步补偿结果Fig.4 Preliminary compensation result
线振动时间约为10 min,考察补偿前后的纯惯导速度误差。从图3可以看出,线振动开始后水平方向加速度、角速率乘积项所对应的积分值迅速增大,说明加速度和角速率之间耦合作用明显,造成了相应的姿态漂移。进一步,从图4可以看出,线振动条件下由于加速度和角速率之间的耦合作用,惯导系统速度误差迅速增大,经过补偿后速度误差减小 30%以上,精度改善明显。
4 结 论
机抖激光陀螺敏感轴动态偏移误差是造成振动环境下惯导系统精度下降的重要原因,本文建立了机抖激光陀螺敏感轴动态偏移的误差模型,根据误差模型设计了相应的误差参数标定方法,并探讨了标定实验的组织实施形式。初步的实验结果表明,机抖激光陀螺敏感轴动态偏移误差补偿后,10 min线振动时间内,系统纯惯导速度误差减小30%以上。
(References):
[1] 刘昱, 王伟, 李城锁. 激光陀螺捷联惯导系统 IMU结构模态分析[J]. 中国惯性技术学报, 2012, 20(3): 273-277. Liu Yu, Wang Wei, Li Cheng-suo. Modal analysis for IMU of ring laser gyro strap-down inertial navigation system[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 273-277.
[2] 章博, 任娟. 捷联惯组空间五点减振的振动耦合分析[J]. 宇航学报, 2015, 36(9): 1030-1035. Zhang Bo, Ren Juan. Coupling vibration analysis of spatial-five-point arrangement isolators for strapdown inertial navigation system[J]. Journal of Astronautics, 2015, 36(9): 1030-1035.
[3] Li J L, Fang J C, Ge S S. Kinetics and design of a mechanically dithered ring laser gyroscope position and orientation system[J]. IEEE Transactions on Instrumentation and Measurement, 2013, 62(1): 210-220.
[4] Cheng J C, Fang J C, Wu W R, et al. Optimized design method of vibration isolation system in mechanically dithered RLG POS based on motion decoupling[J]. Measurement, 2014, 48: 314-324.
[5] Zlatkin Y M, Kainoguz A N, Voronchenko V G, et al. Laser SINS for Cyclone-4 launch vehicle[J]. Gyroscope and Navigation, 2013, 4(3): 156-163.
[6] Paul G S. Blazing gyros: the evolution of strapdown inertial navigation technology for aircraft[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 637-655.
[7] Yu X D, Wei G, Long X W, et al. Finite element analysis and optimization of dither mechanism in dithered ring laser gyroscope[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(3): 415-421.
[8] Yu X D, Long X W. Parametric design of mechanical dither with bimorph piezoelectric actuator for ring laser gyroscope[J]. International Journal of Applied Electromagnetics and Mechanics, 2015, 47(2): 305-312.
[9] 赵小宁, 韩宗虎, 郭昕, 等. 椭圆锥动效应对机械抖动激光陀螺振动特性的影响[J]. 中国惯性技术学报, 2015, 23(2): 258-261. Zhao Xiao-ning, Han Zong-hu, Guo Xin, et al. Influence of elliptical coning motion effect on mechanically dithered RLG vibration performance[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 258-261.
[10] Kim K, Park C G. Drift error analysis caused by RLG dither axis bending[J]. Sensors and Actuators, 2007, 133(2): 425-430.
Estimation and compensation for dynamic bending error parameters of mechanical dithered RLG sensitive axis
WANG Lin, WU Wen-qi, PAN Xian-fei, LI Geng
(1. College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, China; 2. College of Optoelectronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)
The dynamic bending error model of mechanical dithered RLG sensitive axis is derived to improve the navigation accuracy of SINS in vibration environment. In view of engineering application, a simplified dynamic bending error model of mechanical dithered RLG sensitive axis is established. Based on the simplified error model, the equivalent gyro drift’s coupling relationships with the specific force and the angular rate are derived, in which the equivalent gyro drift is caused by the dynamic bending errors of gyro sensitive axis. The dynamic bending errors are attributed to nine unknown parameters. To identify these parameters, a calibrate method is designed, and the principle for designing the calibration experiment is presented. Vibration experiments based on attitude error observations are conducted to estimate the unknown parameters, which show that the velocity error is decreased by 30% after compensating the dynamic bending errors within 10 min of linear vibration.
mechanical dithered RLG; sensitive axis dynamic bending; error model; parameter calibration
U666.1
:A
2016-08-06;
:2016-11-29
国家重大基础研究计划资助项目(6132180103-2);专利申请号(201610543153.X)
王林(1987—),男,博士研究生,从事惯性导航系统研究。E-mail: wanglinshanda@163.com
联 系 人:吴文启(1967—),男,教授,博士生导师。E-mail: wenqiwu_lit@hotmail.com
1005-6734(2016)06-0828-04
10.13695/j.cnki.12-1222/o3.2016.06.023

