基于hp自适应伪谱法的组合动力可重复使用运载器轨迹优化
周宏宇,王小刚,崔乃刚,郎 博
(1. 哈尔滨工业大学 航天学院,哈尔滨 150001;2. 国营第六二四厂,哈尔滨 150030)
基于hp自适应伪谱法的组合动力可重复使用运载器轨迹优化
周宏宇1,王小刚1,崔乃刚1,郎 博2
(1. 哈尔滨工业大学 航天学院,哈尔滨 150001;2. 国营第六二四厂,哈尔滨 150030)
针对传统化学火箭难以重复使用、发射成本高的问题,提出了一种水平起飞/降落的新一代可重复使用运载器飞行方案,并对其动力模式设计和上升段轨迹优化方法等关键技术进行深入研究。设计了一种涡轮冲压发动机结合火箭冲压发动机的组合动力模式,建立了发动机推力与高度、马赫数等变量间的耦合模型,根据动力形式将上升段轨迹分为两段并采用全局搜索法确定动力切换的最佳时机。根据分段结果,分别以燃料最省和终端速度最大为指标,利用 hp自适应伪谱法对两段进行轨迹优化设计。该算法基于双层策略求解最优控制问题,兼备伪谱法和有限元法的优点,与打靶法、伪谱法和间接法相比,初值更易选取,收敛速度更快。
hp自适应伪谱法;组合动力;可重复使用运载器;轨迹优化
载人航天的发展历程可分为载人飞船和航天飞机两个阶段。载人飞船发射成本高,发射准备周期长,航天员受到的过载很大,只能一次性使用;航天飞机的助推火箭是一次性的,维护成本高,危险性高,缺少逃生系统。针对上述两种运载方式的不足,各航天强国纷纷提出新的载人航天策略[1],着手设计可重复使用的新一代载人航天运载器,其中,水平起飞/降落的方式是目前的研究热点之一。
动力系统是航天运载器的关键部分,当前飞行器的主要动力装置有涡轮、冲压和火箭等三种形式,它们适用于不同的飞行条件,单一的某种动力形式不能同时实现可重复使用和载人航天任务这两个目标。文献[2]研究了TBCC(涡轮基组合循环发动机)动力装置并联方案,完成了涡扇/冲压发动机的总体性能方案设计,但只适用于0~5 Ma和H=0~30 km的工作范围;文献[3]指出RBCC(火箭基组合循环发动机)包含多个工作模态,具有工作速域宽、空域广的优点,兼具加速和巡航能力,但它必须达到一定速度后才能启用。TBCC和 RBCC发动机有着各自的优缺点和适用环境,若将两者结合形成组合动力发动机,取长补短,便能够在完成航天任务的同时实现运载器的可重复使用。为了充分发挥组合动力的优势,必须确定两种动力模式的最佳切换时机,并据此对不同飞行阶段进行轨迹优化设计,从而获得最大的运载能力。
对于涉及复杂动力形式和复杂高超声速动力学特性的优化问题而言,打靶法、常规伪谱法和间接法等并不适用。文献[4]通过简化动力学模型,利用间接法实现了高超声速飞行器轨迹快速优化,但发动机模型过于简化;文献[5]针对含有复杂约束条件的非线性最优控制问题,提出了改进的高斯伪谱法,但存在初始不易选择,为提高精度必须增加时间节点的缺点。
本文提出了一种TBCC配合RBCC使用的动力模式,并建立了相应的推力、比冲模型,使动力系统在各种飞行状态下都能获得良好的动力性能;然后依据动力形式将飞行轨迹分段,针对不同阶段的动力特性、任务和环境因素选用不同的控制量、约束条件和性能指标,采用hp自适应伪谱法进行分段轨迹优化,并利用全局搜索法确定最佳动力切换时机,提高优化效率;最后进行了仿真验证。
1 动力系统建模
1.1 动力模式
组合推进技术不仅在理论上成立,而且已被工程实践证明是合理可行的[3]。本文采用TBCC与RBCC相结合的动力模式。TBCC实现涡轮/冲压变循环工作过程,能在低速、低空环境下得到良好的推进性能;RBCC将火箭和冲压发动机结合,在空气稀薄处高速飞行时仍能获得良好的推进性能[6]。飞行器在 TBCC的作用下飞行,达到一定高度和速度后切换到RBCC,并最终完成上升段飞行,切换的高度和速度(或马赫数)即为切换时机,分别记为Hqh和Vqh(或Mqh)。
1.2 TBCC发动机模型
对于TBCC发动机,认为推力和比冲是飞行高度和飞行马赫数的函数:

式中:P为发动机推力,Is为发动机比冲,H为飞行高度,Ma为飞行马赫数。
为便于分析,参考常见的TBCC动力特性和参数,通过多项式计算单位捕获面积上的推力和比冲:

1.3 RBCC发动机模型
对于RBCC发动机,推力和比冲是飞行高度、飞行马赫数和火箭发动机秒耗量的函数。

火箭发动机的秒耗量越大,冲压发动机所占比重就越小;若发动机推力越大,则比冲就越小。为了便于分析,将RBCC发动机单位捕获面积上的推力和比冲看作是火箭发动机所占比重的函数:

式中:Tmax为发动机最大推力,Imax为发动机最大比冲,K∈[0,1]表示节流阀(火箭发动机所占比重)。这样就可以通过控制火箭发动机秒耗量(节流阀)来调节推力。本文取Tmax=360 kN,Imax=3000s。
计算出推力和比冲后,分别乘以发动机捕获面积SC即得到实际推力和比冲。
2 数学模型建立
2.1 动力学模型
为便于研究轨迹设计问题,假设飞行器无侧向运动,不考虑地球扁率与旋转,可得飞行器质心运动方程如下:

式中:V为飞行速度大小,m为飞行器质量,α为攻角,g为重力加速度大小,γ为飞行路径角,R为飞行器到地心的距离,X和Y分别为阻力和升力。

式中:q为飞行动压,S为特征面积;cx和cy分别为阻力系数和升力系数。参考常见的高超声速飞行器的气动特征,本文采用多项式计算气动系数:

2.2 优化模型
一般的非线性系统状态方程为如下所示[7]:

式中:x∈Rn为状态变量,u∈Rm为控制变量。边界条件为:
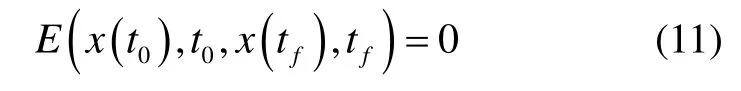
路径约束或控制约束为:

考虑上面的一般非线性系统,优化问题可表述为:在满足状态方程、边界条件和路径约束的条件下,求解控制变量u,使以下性能指标达到极小:
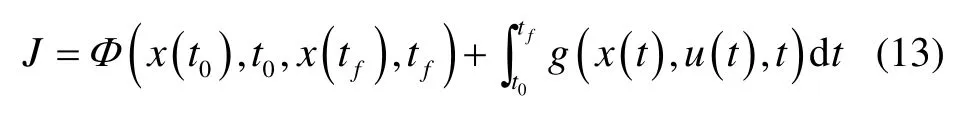
式中:Φ为终端型指标,g为积分型指标。
3 上升段轨迹优化
3.1 hp自适应伪谱法
hp自适应伪谱法将Radau伪谱法与hp型有限元法结合,在一系列离散点上利用全局多项式近似微分方程,将最优控制问题的求解转化为对非线性规划(Nonlinear Programing, NLP)问题[8]的求解。
3.1.1 最优控制问题转化
将最优控制问题的时间区间t∈[t0,tf]划分为K个网格(子区间),并将每个时间区间t∈[tk-1,tk]转换至τ∈[-1,1],即
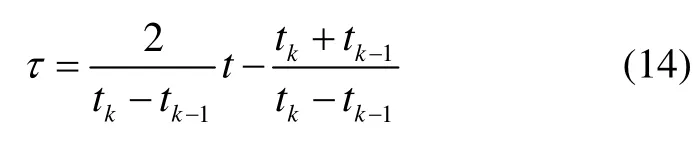
式中:k=1,2,…,K ;tk=tf。
状态量在第k个网格上可近似表示为:

式中:X(k)(τ)为第k个网格上状态量的近似值,表示为τ的函数;Nk为第k个网格上的 Lagrange-Gauss-Radau配点数;τj为第k个网格的节点,当j∈[1,Nk]时,τj为配点,当j=Nk+1时,τj为端点,表示终端时刻;Xj为τj处的状态量的值,Lj为τj处的Lagrange多项式。
结合式(10)和式(15)可得:

只考虑终端型指标,则目标函数可近似表示为:

将不等式约束在第k个网格上用Nk个配点离散化处理:

边界约束条件可近似表示为:

为了保证网格的连续性,需满足:

上述离散过程将最优控制问题转化为非线性规划问题,可以利用SNOPT[9]等软件包进行求解。
3.1.2 hp自适应更新判定准则
在每个网格内设定最大容许误差 εc,如果第k个网格的最大误差,则需对该网格进行重新细化。细化方法有两种:1)增加网格内插值多项式的阶次p(即Nk);2)在网格内插入h个网点,将该网格细分为(h+1)个网格。
当网格需重新细化时,首先要判定应该增加p还是h。设网格内的第i个状态分量的曲率函数为:


3.1.3 更新变量计算公式
若增加p,则新的插值多项式的阶次p1为

式中:p0为更新前的插值多项式阶次,ceil()为正向舍入函数,A为自定义参数。
若增加h,则新增网点数h1为

式中:B为自定义参数。
3.1.4 hp自适应伪谱法计算流程
hp自适应伪谱法计算步骤如下所示,算法流程图如图1所示。具体流程为:
1)按照划分好的网格,将最优控制问题转化为NLP问题,并对NLP问题进行求解;
3)如果rk<rkmax,将网格内插值多项式的阶次增加为p1,否则将网数增加为h1;
4)如果状态量和路径约束的相对误差满足要求,则优化结束,否则返回步骤1)。

图1 hp自适应伪谱法流程图Fig.1 Flow chart of hp-adaptive pseudo-spectral method
从以上过程可以看出,该算法较伪谱法而言,减少了多项式阶次(配点)的增加,进而减小了NLP问题的规模,有利于提高收敛速度;另外,多项式阶次过高会使得输出对输入过于敏感,导致问题病态,该算法恰好可以避免这一点。
3.2 轨迹分段方法
TBCC发动机特性如图2所示,可以看出:在高度20 km以上时,推力随马赫数变化不大,且数值较小,因此Hqh不宜超过25 km;但Hqh过低,大气密度会较大,导致动压很大,不适合RBCC工作,不利于后续爬升,故设定Hqh不低于10 km。
此外,TBCC的工作马赫数一般不超过5。因此,本文将切换参数的范围限定为:10≤Hqh≤25,2≤Mqh≤4。通过分析发动机特性进而缩小切换时机的选择范围,有利于提高计算速度和效率。

图2 TBCC发动机特性Fig.2 Feature of the engine with turbo-based combined cycle
4 仿真分析
4.1 仿真初始条件
采用 hp自适应伪谱法对飞行器上升轨迹进行优化,并采用全局搜索法[10]在之前划定的范围内确定发动机切换状态Hqh和Mqh。
飞行器特征面积63 m2,发动机捕获面积17 m2,TBCC段性能指标为燃料消耗最少,控制变量为攻角α;RBCC段性能指标为终端速度最大,控制变量为攻角α和发动机相对流量K。飞行器初始状态、终端状态,以及搜索出的切换状态如表1所示。

表1 初始及终端运动状态设定Tab.1 Setting of the craft states
对于吸气式高超声速飞行器,为防止发动机熄火,需要将攻角约束在一定范围内,以保证足够的进气量;考虑气动热约束及RBCC工作环境,需要对动压进行约束;出于结构强度的考虑,还需对过载进行约束,具体约束条件见表2。
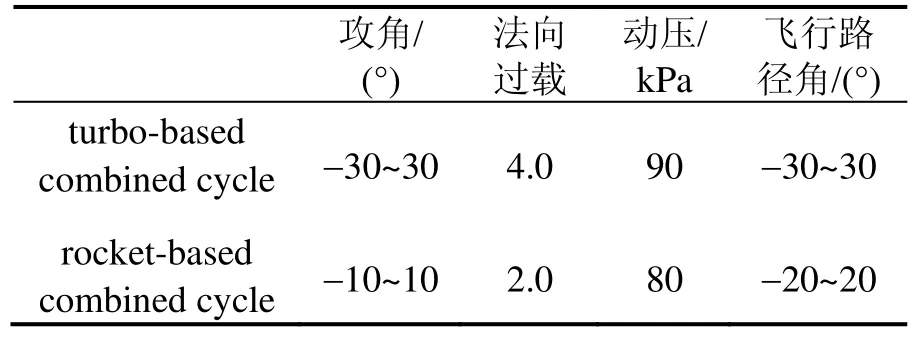
表2 过程约束设定Tab.2 Setting of the course constrains
4.2 仿真结果
TBCC段燃料消耗14 037 kg,飞行108.57 s;RBCC段结束时速度为4 951.53 m/s,飞行300 s。相关仿真结果图像如图3~9所示。

图3 飞行攻角Fig.3 Time history of attack angle

图4 速度变化情况Fig.4 Time history of velocity
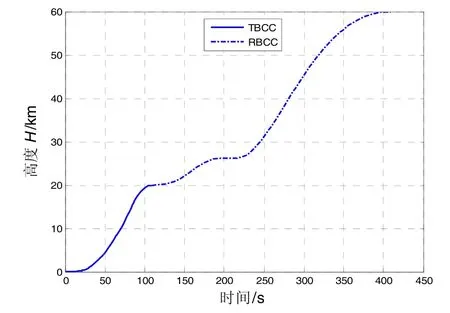
图5 高度变化情况Fig.5 Time history of height

图6 飞行路径角变化情况Fig.6 Time history of path angle
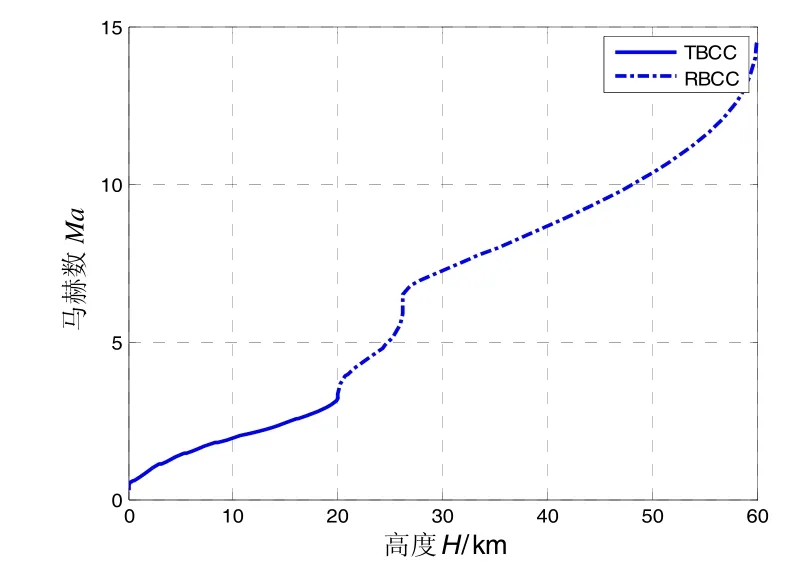
图7 飞行剖面Fig.7 Flight profile

图8 飞行过程变量Fig.8 Time history of course variety

图9 相对流量变化情况Fig.9 Time history of relative flow
从仿真结果可以看出,优化出的轨迹能够满足过程约束、控制约束和终端约束,且结果合理可行。
图3中的攻角在动力切换时发生了突变,这是由于攻角作为控制量在仿真中并未对其连续性进行约束,而法向过载是与攻角有关的量,因此图8中的法向过载也在同一时刻产生了突变。在实际应用中,可以在TBCC段结束时,先通过姿控将飞行器攻角调整至RBCC段的起始攻角,然后再开机。
5 结 论
本文针对载人航天任务未来的发展趋势,设计了一种组合动力模式,并采用优化方法进行了轨迹优化设计。具体如下:
1)对飞行器的动力模式进行了分析、设计,建立了与飞行环境相耦合的发动机模型,更利于轨迹优化设计。
2)为处理复杂优化问题,采用了hp自适应伪谱法,根据不同动力形式将上升段飞行分段并结合各段的特点,分别选取不同的控制量、过程约束和性能指标进行分段优化。
3)为提高优化效率,尽可能提高性能指标,关键在于确定各段之间的切换时机。通过分析飞行器动力特点缩小了切换时机选取范围,然后采用全局搜索法结合hp自适应伪谱法的方法确定切换时机,并据此进行分段优化。
(References):
[1] 孙龙, 刘映国. 2011年世界载人航天发展综合分析[J].载人航天, 2012, 18(1): 92-96. Sun Long, Liu Ying-guo. A comprehensive analysis of the world manned spaceflight development in 2011[J]. Manned Spaceflight, 2012, 18(1): 92-96.
[2] Zhang H J, Liu X G, Guo R W. Design of turbo diffuser for TBCC inlet based on characteristics of turbo mode[J]. Journal of Aerospace Power, 2014(1): 181-191.
[3] 何国强, 秦飞, 魏祥庚, 等. 火箭冲压组合发动机燃烧的若干基础问题研究[J]. 实验流体力学, 2016, 30(1): 1-14. He Guo-qiang, Qin Fei, Wei Xiang-geng, et al. Investigation of several fundamental combustion problems in rocket based combined-cycle engines[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(1): 1-14.
[4] Murillo O. Fast ascent trajectory optimization for hypersonic air-breathing vehicles[C]//AIAA Guidance, Navigation, and Control Conference. 2010: 14-38.
[5] 孙勇. 基于改进 Gauss伪谱法的高超声速飞行器轨迹优化与制导[D]. 哈尔滨工业大学, 2012: 42-46. Sun Yong. Trajectory optimization and guidance of hypersonic vehicle based on improved gauss pseudospectral method[D]. Harbin, China: Harbin Institute of Technology, 2012: 42-46.
[6] Gong C, Chen B, Gu L. Design and optimization of RBCC powered suborbital reusable launch vehicle[C]// AIAA International Space Planes and Hypersonic Systems and Technologies Conference. 2014: 26-47.
[7] Song C, Zhao G, Chen J. Reentry trajectory optimization for hypersonic vehicle based on GPM[C]//Proceedings of the 2012 Second International Conference on Electric Information and Control Engineering. 2012: 1183-1186.
[8] Tohidi E, Lotfi N S. An efficient legendre pseudospectral method for solving nonlinear quasi bang-bang optimal control problems[J]. Journal of Applied Mathematics, Statistics and Informatics, 2012, 8(2): 73-85.
[9] Conte J P. OpenSees-SNOPT framework for finite elementbased optimization of structural and geotechnical systems[J]. Journal of Structural Engineering, 2012, 137 (6): 822-834.
[10] Crouser R J, Schmidt M C, Kelley S, et al. Global pattern search at scale[C]//IEEE International Symposium on Technologies for Homeland Security. IEEE, 2015: 1-6.
Trajectory optimization of reusable vehicle with combined power based on hp adaptive pseudospectral algorithm
ZHOU Hong-yu1, WANG Xiao-gang1, CUI Nai-gang1, LANG Bo2
(1. Department of Astronautics, Harbin Institute of Technology, Harbin 150001, China; 2. Stale-owned Factory No.624, Harbin 150030, China)
In view that traditional chemical rocket is hard to be reused and suffers from high launch cost, a novel flight scheme based on horizontally taking off and landing is proposed, by which a vehicle can be completely reusable. The power mode and the optimization algorithm of the ascend trajectory are designed. A combined power mode of turbo-based combined cycle and rocket-based combined cycle is presented, and the engine model is built based on the relationship between thrust and height/velocity. Then the ascend trajectory is divided into two phases depending on the power mode. A universal searching method is employed to confirm the best opportunity in changing the engine mode, and an hp-adaptive pseudospectral method (HPM) is developed, which takes into account the influences of various constrains and value functions on the results of the universal searching method in different phases. The HPM adopts dual-layer strategy to solve the optimal control problem, and has both the merits of the finite element method and the pseudo-spectral method. The HPM can choose the initial value more easily, and has even faster convergence speed, compared with the shooting method, the pseudo- spectral method and the indirect method.
hp-adaptive pseudospectral; combined power; reusable vehicle; trajectory optimization
V412.4
:A
2016-09-02;
:2016-11-30
国家自然科学基金(61304236)
周宏宇(1991—),男,博士研究生,研究方向为飞行器制导与优化。E-mail: 826867857@qq.com
联 系 人:王小刚(1980—),男,副教授,研究方向为非线性滤波理论及应用。E-mail: wangxiaogang@hit.edu.cn
1005-6734(2016)06-0832-06
10.13695/j.cnki.12-1222/o3.2016.06.024

