基于横向地球坐标的惯性导航方法

王海波，张汉武,，张萍萍，王 军，郝勇帅,

（1. 海军大连舰艇学院 航海系，大连 116018；2. 海军大连舰艇学院 研究生管理大队，大连 116018；3. 海军大连舰艇学院 导弹系，大连 116018）

基于横向地球坐标的惯性导航方法

王海波1，张汉武1,2，张萍萍2，王 军3，郝勇帅1,2

（1. 海军大连舰艇学院 航海系，大连 116018；2. 海军大连舰艇学院 研究生管理大队，大连 116018；3. 海军大连舰艇学院 导弹系，大连 116018）

针对极区经线迅速收敛于极点造成的传统惯导机械编排在极区不适用问题，提出了CGCS2000地球椭球体模型下基于横向地球坐标的惯性导航方法。在构建横向坐标系及伪经纬网的基础上，给出了横向惯导与传统惯导间导航参数的转换关系，推导了横向地理坐标系机械编排，建立了系统误差模型，并以某型船舶为例，通过系统性能的静基座、动基座仿真分析，研究了基于横向地球坐标的惯性导航方法在极区的适用性。仿真分析表明，基于横向地球坐标的惯性导航方法可以克服传统惯导在极区存在的问题，在极点处不存在计算溢出，并可为载体穿越极点时提供高精度的姿态、位置信息，适用于极区。

惯性导航；地球椭球体模型；横向地球坐标；极区

现代导航均以经线作为航向参考基准，位置采用经纬度坐标来表示，而由于经线收敛于极点，使得在极区难以建立相对经线的航向参考基准，为极区导航带来了困难，这也是导致传统惯性导航系统在极区无法定向、定位的原因[1-5]。游动方位惯性导航方法是解决极区导航问题的一种方法，但在近极点区域使用时，存在难以区分游动方位角和经度值等缺陷。这是由经纬度描述载体位置的局限性造成的[6-7]。而格网导航[8]并没有改变极区经线收敛的问题，在近极点区域存在经纬度误差放大的缺点[9]。

为解决传统惯导在极区存在的问题，文献[10]首先提出了横向坐标系。文献[11-12]对横向惯性导航做了详细的分析，并提出了相应的阻尼方案，但地球模型使用的是圆球模型，导航算法带有原理误差。文献[13]也存在地球模型选用圆球的问题。文献[14]选用了WGS-84地球模型，但是其关于横向经纬度的定义较为模糊，导航解算时，必须以传统惯导中解算的相关信息作为中间量，导航解算的思想与格网导航类似[14]。鉴于此，本文选用CGCS2000地球椭球体模型，对基于横向地球坐标的惯性导航方法进行研究。

1 基于横向地球坐标的惯导机械编排

1.1 坐标系与伪经纬网的构建

采用CGCS2000地球椭球体模型，构建横向坐标系及伪经纬网。

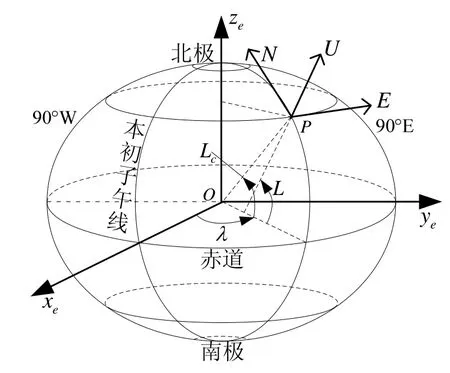
图1 地球坐标系与地理坐标系Fig.1 Terrestrial coordinate and geographic coordinate system

1）横向地球坐标系（E系）。将图1中的地球坐标系（e系）Oxeyeze先绕Oxe轴旋转-90°得到Oxeye′zE，再将Oxeye′zE绕OzE轴旋转-90°得到图2所示的横向地球坐标系OxEyEzE。旋转后得到的横向地球坐标系的OxE轴与Oxeyeze的Oze轴重合，OyE轴与Oxeyeze的Oxe轴重合，OzE轴与Oxeyeze的Oye轴重合。

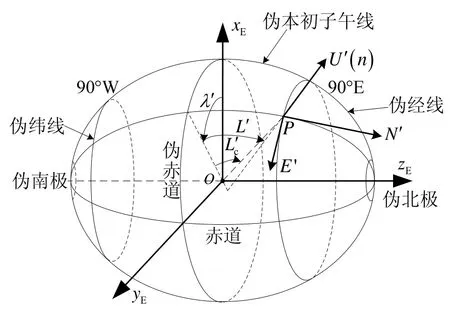
图2 横向坐标系与伪经纬网Fig.2 Transverse coordinate system and false graticules

2）构建伪经纬网。极点处子午线汇聚成一点是引起定向与定位难题的根本原因，为适应极区导航的需要，本文基于横向地球坐标系构建图2所示的伪经纬网，建立横向地球坐标（伪经纬度），其中，90°E与赤道的交点定义为伪北极点N′，90°W与赤道的交点定义为伪南极点S′，0°与180°经线为伪赤道，北半球的90°W与90°E经线构成伪本初子午线。定义伪地轴为通过伪南北极点的直线，伪子午圈（伪子午圈）为地球上通过伪南北极点的平面截地球椭球面所得的平面曲线，而伪纬线圈（伪纬线）则被视为P点处的圆，圆的半径为P点到伪地轴的距离。这样，伪南北极点分伪子午圈所成的半圆伪经线指示伪南北方向，伪纬线指示伪东西方向。定义伪经度λ′为通过P点的伪子午面与伪本初子午面所成的二面角，伪纬度（也叫作伪地理纬度）L′为地球伪子午圈上P点法线n与地球伪赤道平面的夹角。

3）横向地理坐标系（T系）。基于构建的伪经纬线网建立P点处的横向地理坐标系PE′NU′′（伪东北天），其中：PN′与P点处伪经线相切，指向伪北N'；PU′沿P点处伪经线的垂线方向，指向伪天U′；PE′通过右手法则确定，指向伪东E′。

1.2 导航参数转换

当船舶在中低纬度地区航行时，一般仍使用传统惯性导航系统机械编排；当船舶航行至极区时，需将惯导机械编排切换为基于横向地球坐标的惯导机械编排。为使系统机械编排与传统机械编排在全球范围内切换时准确、平稳过渡，需将两种机械编排中的定向定位参数进行精确的转换[12]。

1.2.1 姿态信息的转换

值得注意的是，建立的横向地理坐标系除载体在极点处时为当地水平坐标系，其他情况下，横向地理坐标系的PU′轴与地理坐标系（t系)的PU轴在PN′轴方向上有一夹角1σ，如图3所示。

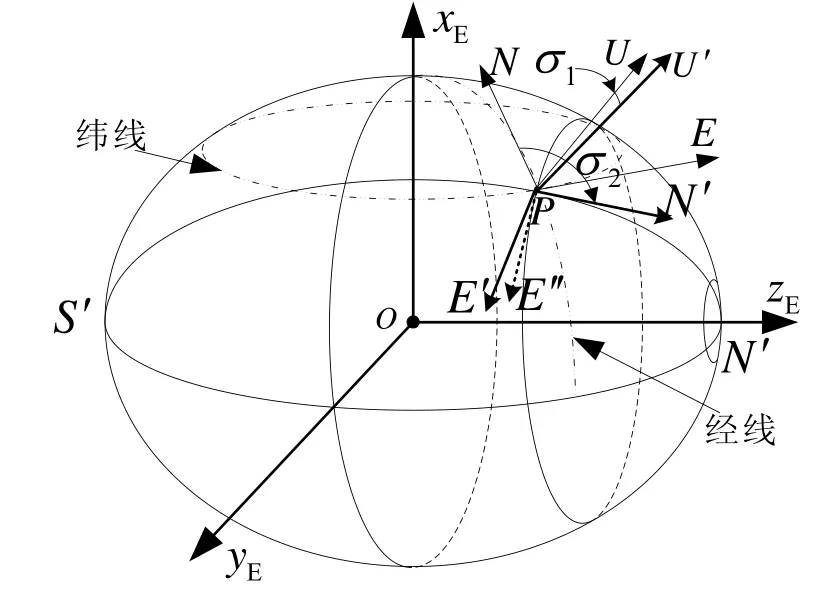
图3 横向地理坐标系与地理坐标系间的关系Fig.3 Relationship between geographic coordinate system and transverse geographic coordinate system

通过三余弦定理求得：

从图3可以看出，地理坐标系变换到横向地球坐标系，经过了两次转动，两次转动的欧拉角分别为2σ、1σ，转动的过程可以表示为

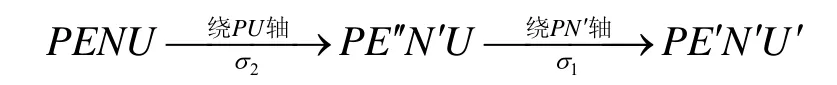
所以，横向地理坐标系与地理坐标系间的变换矩阵为

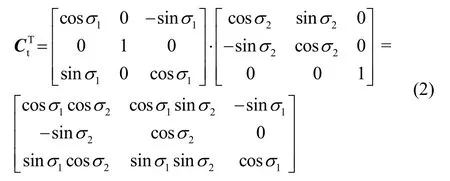
地球坐标系与横向地理坐标系间的变换矩阵为

式(3)中，

根据坐标系间的变换关系，地球坐标系与横向地理坐标系间的变换矩阵也可以表示为

式(6)中，

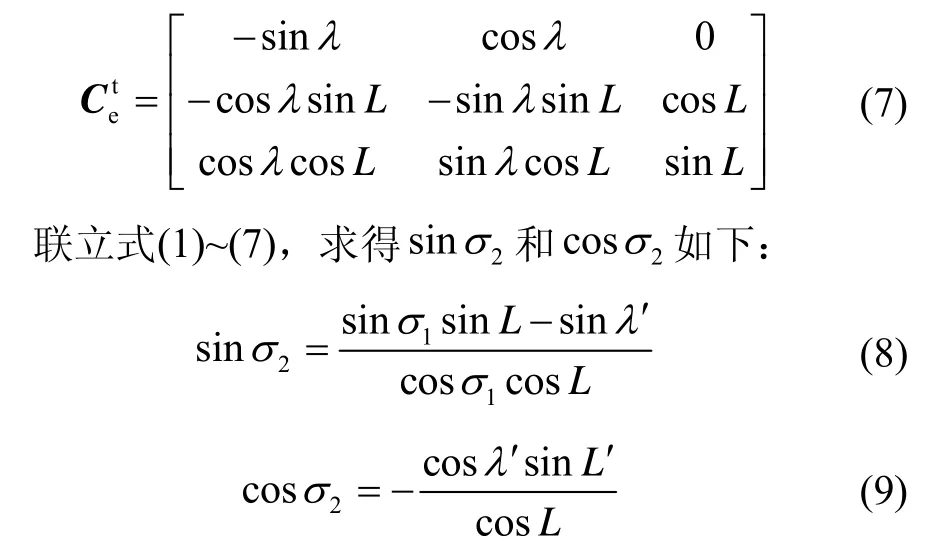
在传统惯导中，姿态矩阵有：

式(10)是关于载体姿态(纵摇角θ、横摇角φ、航向角ψ)的函数，若知道了Ct的元素值，便可计算出ψ、θ、b φ。同理，姿态矩阵CbT是关于载体伪姿态（伪纵摇角θ′、伪横摇角φ′、伪航向角ψ′）的函数，如下：

式(12)由式(2)、式(10)求得：

1.2.2 速度信息的转换

横向地理坐标系中的地速VT与地理坐标系中的地速Vt的转换为

1.2.3 位置信息的转换

记P点到地心的距离OP为ROP，P点相对于地心的位置矢量在e系和E系中的数学矢量分别记作Re、RE，则有：

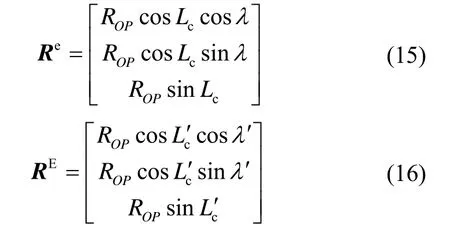
e系中的位置矢量Re转换为E系中的RE，通过下式进行转换：

地理纬度与地心纬度的转换关系为

伪纬度与伪地心纬度的转换关系为

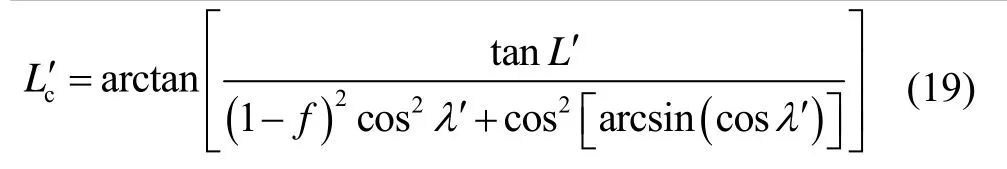
联立式(3)及式(15)～(19)得经纬度与伪经纬度的主值关系：

1.3 横向地理坐标系机械编排

以横向地理坐标系为导航坐标系，机械编排与传统惯导机械编排相比，微分方程形式基本保持不变。

1）伪姿态微分方程

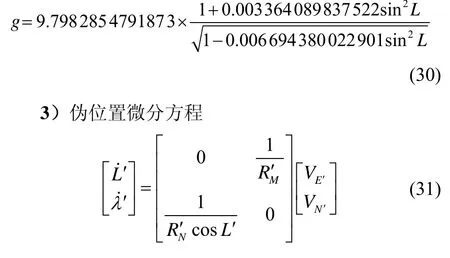
2 系统性能仿真分析

为研究基于横向地球坐标的惯导系统的工作性能，以某型船舶为例，只考虑平静海况下，船舶在地球表面的运动，故屏蔽位置、速度的垂直通道。

2.1 系统误差模型

根据1.3节的机械编排，忽略重力误差并略去二阶小量，只考虑陀螺仪漂移εb以及加速度计零偏∇b，记伪姿态误差角为推导出如下误差方程：

记状态变量为

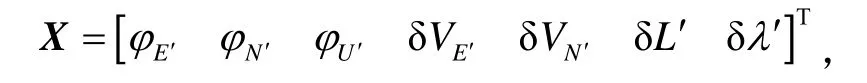
则式(32)中各式可组合为如下单矩阵系统误差方程：

式(33)中：B表示陀螺仪常值漂移和加速度计零偏项；W表示陀螺仪、加速度计随机误差项；F为系统状态矩阵，表示如下：

2.2 系统性能静基座仿真分析

仿真结果如图4所示，从图中可以看出，静基座下水平伪姿态角误差在36h内小于0.6′，伪航向角误差在36h内不超过3.1′且是发散的，水平伪速度误差不超过 3kn，伪经纬度误差不超过 0.02°。因此，静基座下基于横向地球坐标的惯导机械编排在极区提供的位置、姿态精度比较高。同时，可以看到图4的各误差曲线均比较平滑，没有出现跳变现象，说明所研究的系统在地理极点处不存在计算溢出的问题。

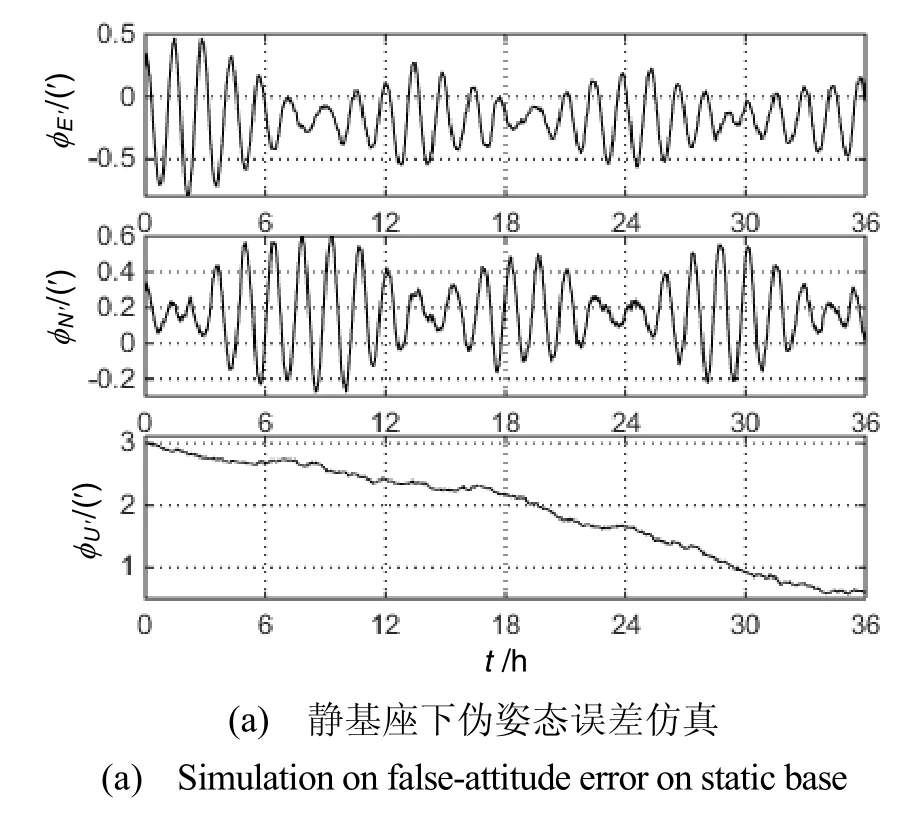
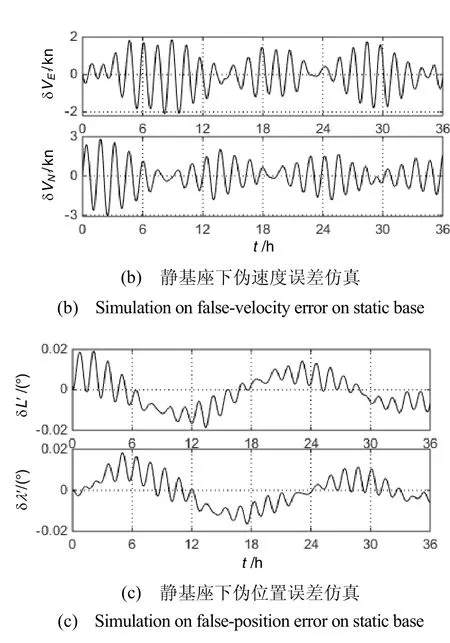
图4 静基座下系统性能仿真Fig.4 Simulation on system performance on static base

2.3 系统性能动基座仿真分析

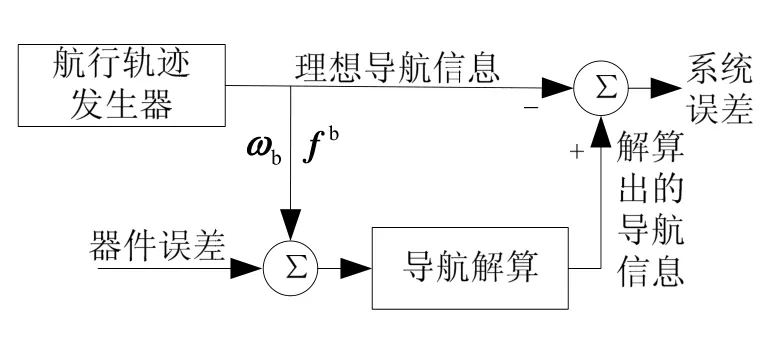
图5 系统动基座仿真方框图Fig.5 Simulation of system on dynamic base

动基座下的系统性能与静基座下的不同，式(33)表示的系统误差方程复杂而且时变。文献[13]只针对载体匀速穿过北极点的条件进行了仿真，不能得到载体复杂运动状态下系统的导航精度。如图5所示，以某型船舶为例，利用轨迹发生器为其规划一条精确的穿越极点的航迹（为简单起见，航迹为沿子午线的一条直线，船舶伪姿态为0），从而获得惯性器件、导航信息的理想输出，同时根据系统误差模型产生惯性器件误差叠加于理想值之上，作为导航解算的输入，进而通过将解算出的导航信息与理想导航信息作差，获得系统误差。仿真参数设置与2.2节相同。船舶航迹规划为：初始位置[89.8°N, 90°W](伪经纬网中的位置[0.2°S′, 0])，船舶运动状态如图6(b)，航行时间为2h，大约航行 1.5h后穿越北极点，停车位置[89.7°N, 90°E](伪经纬网中的位置[0.3°N′, 0])。航迹输出的理想导航信息如图6所示。船舶的理想航迹如图8中虚线所示。

图6 理想导航信息Fig.6 Ideal navigation information

根据规划的航迹得到惯性器件的输出后，考虑惯性器件的误差以及初始伪姿态、初始伪速度、初始伪位置误差并进行导航解算，将解算出的导航信息与理想导航信息作差，得到船舶在平静海况下做复杂运动的系统误差曲线，如图7所示。船舶的实际航迹如图8中实线所示。

图7 动基座下系统性能仿真Fig.7 Error curves of the system on dynamic base

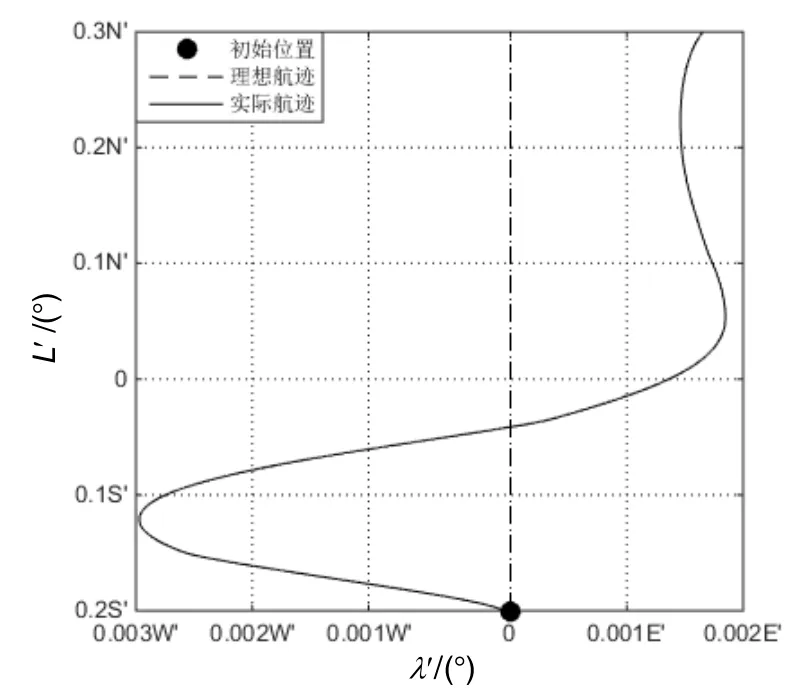
图8 伪经纬网中标示的船舶航迹Fig.8 Ship’s track marked on false graticules

分析图7所示的系统误差曲线可知：在2h内伪纵摇角误差不超过1′，伪横摇角误差不超过0.4′，伪航向角误差不超过3′；伪东向速度误差不超过1kn，伪北向速度误差不超过2.5 kn；伪纬度误差不超过0.02°，伪经度误差不超过0.004°。此外，在船舶航行1.5 h左右穿越极点的过程中，伪北航向误差未发生跳变。由此可见，基于横向地球坐标的惯性导航系统用于极区没有机械编排上的缺陷，而且可以为航行的船舶提供高精度的姿态和位置信息。

3 结 论

针对传统惯导机械编排在极区不适用的问题，选用CGCS2000地球椭球体模型，建立了横向地球坐标系，构建了伪经纬线网，给出了伪经纬度及伪地心纬度的定义，建立了地心纬度与伪地心纬度的联系，将经纬度与伪经纬度进行转换，并推导出地球椭球体模型下基于横向地球坐标的惯性导航系统机械编排。根据机械编排推导出了基于横向地球坐标的惯性导航系统误差模型，对动静基座下的系统性能分别进行仿真分析。仿真结果表明，基于横向地球坐标的惯性导航方法适用于极区导航，并且载体穿越极点时也可提供高精度的姿态、位置信息。

（References）：

[1] Davydenko L. Arctic navigation[J]. Polar Navigation, 2015, 2(1): 173-181.

[2] Li Qian, Ben Yue-yang, Yu Fei, et al. Transversal strapdown INS based on reference ellipsoid for vehicle in the polar region[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7791-7795.

[3] Paturel Y, Lacambre J B, Patin F, et al. Inertial navigation at high latitude: trials and test results[M]. New York: OCEANS-IEEE, 2015.

[4] Zhang Hai-feng, Zhang Li-wei, Wang Xing-ling, et al. Optimization design and error analysis of strapdown inertial navigation system mechanization in polar region [J]. Journal of Chinese Inertial Technology, 2015, 23(6): 701-706.

[5] Yang Shuo, Li Qun, Jiang Shu-ming, et al. A damping method for polar navigation based on grid mechanization [J]. Navigation Positioning and Timing, 2016, 3(5): 27-32.

[6] Andriani S, Lysandros T. Choosing a suitable projection for navigation in the arctic[J]. Marine Geodesy, 2013, 36(2): 234-259.

[7] Wang Xian-wei, Cheng Xiao, Hui Feng-ming, et al. Navigation in fast ice near the Zhongshan Station, Antarctica [J]. Marine Technology Society Journal, 2013, 48(1): 84-91.

[8] Maclure K C. Polar navigation[J]. Arctic, 1941, 2(3): 183-194.

[9] Jorg N. Grid navigation with polar stereographic charts[J]. European Journal of Navigation, 2011, 9(1): 4-8.

[10] Broxmeyer C. Inertial navigation system[M]. New York: McGraw-Hill, 1964.

[11] 李倩, 孙枫, 奔粤阳, 等. 横坐标系捷联惯导系统极区导航及阻尼设计[J]. 系统工程与电子技术, 2014, 36(12): 2496-2503. Li Qian, Sun Feng, Ben Yue-yang, et al. Transversal strapdown INS and damping design in polar region[J]. Systems Engineering and Electronics, 2014, 36(12): 2496-2503.

[12] 李倩, 孙枫, 奔粤阳, 等. 基于横坐标系的捷联惯导系统极区导航方法[J]. 中国惯性技术学报, 2014, 22(3): 288-295. Li Qian, Sun Feng, Ben Yue-yang, et al. Polar navigation of strapdown inertial navigation system based on transversal frame in polar region[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 288-295.

[13] 刘文超, 卞鸿巍, 王荣颖, 等. 惯导系统横向坐标法导航性能研究[J]. 武汉大学学报(信息科学版), 2015, 40(11): 1520-1525. Liu Wen-chao, Bian Hong-wei, Wang Rong-ying, et al. Navigation performance of SINS transverse coordinate method[J]. Geomatics and Information Science of Wuhan University, 2015, 40(11): 1520-1525.

[14] 姚逸卿, 徐晓苏, 童金武. 极区间接横向惯性导航方法[J]. 中国惯性技术学报, 2015, 23(1): 29-34. Yao Yi-qing, Xu Xiao-su, Tong Jin-wu. Indirect transverse inertial navigation algorithm in polar region[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 29-34.

Inertial navigation algorithm for polar region based on transverse terrestrial coordinate

WANG Hai-bo1, ZHANG Han-wu1,2, ZHANG Ping-ping2, WANG Jun3, HAO Yong-shuai1,2
(1. Department of Navigation, Dalian Naval Academy, Dalian 116018, China; 2. Administrative Division for Postgraduates, Dalian Naval Academy, Dalian 116018, China; 3. Department of Missile, Dalian Naval Academy, Dalian 116018, China)

Conventional inertial navigation system (INS) mechanization is not applicable in the polar region due to the polar meridians’ quickly converging to the poles. To solve this problem, an inertial navigation algorithm with CGCS2000 earth ellipsoid model is proposed based on transverse terrestrial coordinate. Firstly, by constructing the transverse coordinate system and the false graticules, the navigation parameters’transfor- mational relation between transverse INS and conventional INS was presented. Then, the mechanization based on the transverse geographic coordinate system was deduced, and the error model of the system was established. Finally, by taking a certain type of ship as an example, the applicability of the inertial navigation algorithm based on the transverse terrestrial coordinate in polar region was studied by simulating and analyzing the system performances under the conditions of static base and dynamic base respectively. Simulation and analysis results show that the algorithm can overcome the above problem, and there is no calculation overflow at the poles. It can also provide high-precision attitude and position information for carriers passing through the poles.

inertial navigation system; earth ellipsoid model; transverse terrestrial coordinate; polar region

U666.1

：A

2016-07-12；

：2016-11-16

国防科研基金（DJYKY2014-077）

王海波（1970—），男，高级工程师，主要从事船舶导航技术研究。E-mail: hldwhb@163.com

1005-6734(2016)06-0716-07

10.13695/j.cnki.12-1222/o3.2016.06.004