Transfer alignment of shipborne aircraft with large misalignment based on rotation vector error model

WANG Zhan-qing, LI Li-hua, LIU Xin, ZHANG Yan-shun

(1. School of Automation, Beijing Institution of Technology, Beijing 100081, China; 2. Detection Guidance and Control Technology, Faculty of Aerospace Engineering, Shenyang Aerospace University, Shenyang 110136, China; 3. School of Instrumentation and Optoelectronic Engineering, Beihang University, Beijing 100191, China )

Transfer alignment of shipborne aircraft with large misalignment based on rotation vector error model

WANG Zhan-qing1, LI Li-hua1, LIU Xin2, ZHANG Yan-shun3

(1. School of Automation, Beijing Institution of Technology, Beijing 100081, China; 2. Detection Guidance and Control Technology, Faculty of Aerospace Engineering, Shenyang Aerospace University, Shenyang 110136, China; 3. School of Instrumentation and Optoelectronic Engineering, Beihang University, Beijing 100191, China )

To realize the rapid alignment of the shipborne aircrafts with large initial heading error, a rotation vector error (RVE) model is deduced. The velocity matching and the velocity plus angular rate matching methods are respectively applied to implement the transfer alignment algorithm. In view of the stability and rapidity of nonlinear filter, a square-root unscented Kalman filter is used to estimate the attitude misalignment. Simulation results shows that the rotation vector error model has higher accuracy compared with the nonlinear phi angle model, and by using the velocity plus angular rate matching method, the transfer alignment of shipborne aircraft inertial navigation system can be accomplished in 50 s, and the horizontal and heading precisions are within 20″ and 1′, respectively. These show that the proposed algorithm can meet the rapidity and accuracy requirements of the transfer alignment.

transfer alignment; shipborne aircraft; rotation vector error model; square-root UKF

The shipborne aircrafts’ viability and the shooting percentage of airborne missile are largely determined by the initial alignment of inertial navigation system in shipborne aircraft, thus the alignment should be accomplished accurately and quickly. There are two fundamental types of alignment process: self-alignment, using gyro compassing techniques, and the alignment of a slave inertial navigation system (SINS) with respect to a master inertial navigation system (MINS)-transfer alignment[1]. Due to the influence of complex marine environment and other interference factors, self-alignment can hardly achieve an acceptable accuracy. In this case, the transfer alignment (TA) is normally used to solve the problem[2-4].

The linearized INS error model has been addressed in numerous papers over the last decades. These models can be classified into the Psi-angle, the Phi-angle, equivalent tilt, or additive quaternion error models according to the attitude error states[5]. However, the random position of shipborne aircraft on the carrier would lead to large misalignment between the MINS and SINS. These linear error models can hardly accurately describe the system error propagation properties in the case with large misalignment errors. SUN Changyue proposed a velocity and attitude error propagation model based on the nonlinear phi angle to deal with large initial attitude errors[6]. Xiong Zhilan deduced the multiplicative quaternion and the additive quaternion based nonlinear error models in rapid transfer alignment[7]. However, there are still some defects existing in these large misalignment models, such as singularity in phi angle model[8], large computation costs in quaternion model.

The Extended Kalman Filter (EKF)[9]and Unscented Kalman Filter (UKF)[10]are the most widely used methods for state estimation of nonlinear models. EKF, based upon the principle of linearizing the process and observation models using Taylor series expansions, exist some shortcomings---the difficulties in determining the Jacobians, errors introduced by linearization. To overcome limitations in the EKF, UKF is proposed, which uses the unscented transformation to approximate the probability distribution by a set of deterministically chosen sample points (sigma points), thus avoids the need to use Jacobians in the algorithm. A major drawback of the UKF is its instability due to the numerical calculation error. The covariance matrices may lose their positive semi-definiteness during the filtering procedure[11].

Based on the above considerations, in this paper we proposed a nonlinear model for the shipborne aircraft system with large misalignment. This alignment method used the differences of velocities and the angular rates between MINS and SINS as the measurements. Furthermore, square-root unscented Kalman filter (SRUKF) is used. Compared with UKF, SRUKF can avoid the error covariance matrix losing its non-negative definite and symmetry[12]. In the following sections, simulations are made under the peaceful and medium sea conditions respectively with various kinds of carrier linear motions.

1 State dynamic model for transfer alignment

The coordinates used in the paper are defined as: earth-centered inertial frame (i), earth-centered earthfixed frame (e), navigation frame (n) which aligned with the directions of east, north and up, calculated navigation frame (n′), body frame of master INS (m), body frame of slave INS (s).

1.1 Rotation vector error model

To get the RVE model for the shipborne aircraft system with large misalignment, we need first to introduce some variables as following.

ΔΦn=[Δφ,Δφ,Δφ]T: Rotation vector error (RVE) between the SINS’s true navigation frame (n) and calculated navigation frame (n′), whereΔφE, ΔφNandΔφUare the components of RVE in E, N and U directions.

Where

The relationship between RVE and AQE is derived as

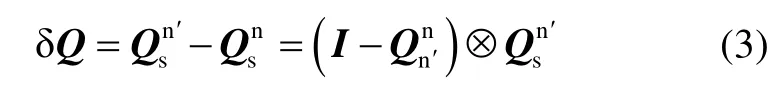
Substituting (1), (2) into (3), we get

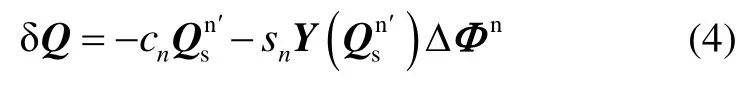
Where

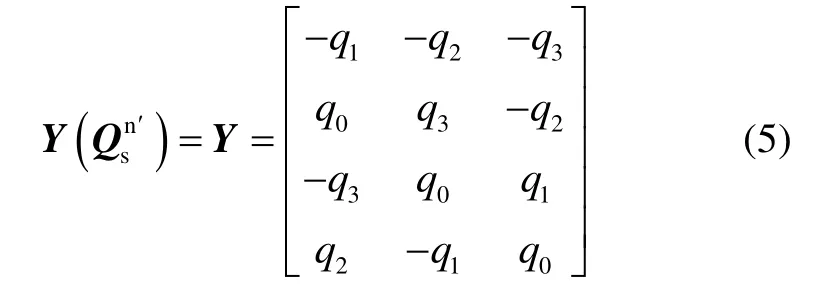
Multiplying both sides of (4) byYT, as YTQsn′=0，YTY=0, so

Differentiating both sides of (6),

Where L, M are represented by

Inserting (4), (8), (11)-(13) into (6), we can get that

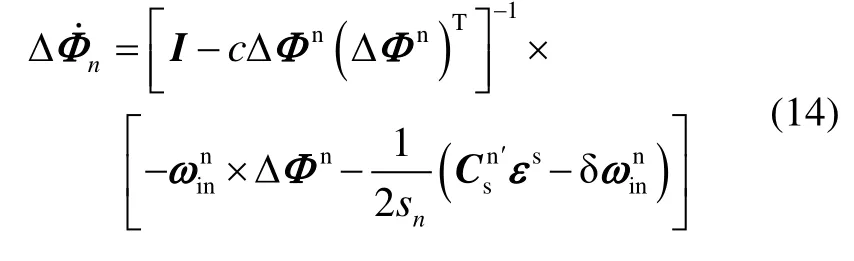
Where

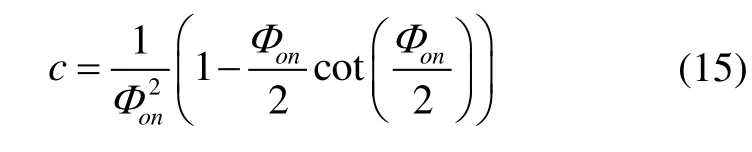
1.2 Velocity error model

Without taking any errors into account, the ideal velocity differential equation of SINS can be expressed as:

Here ∇sis the accelerometer bias in SINS;δωand δωare mainly affected by the positioning error on which the SINS misalignment has little influence, so they can be ignored. Omitting the second order error terms results in the velocity error differential equation (19), we can get that

Where

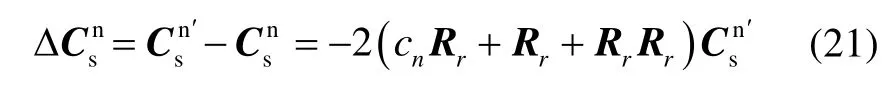
Here Rris defined as

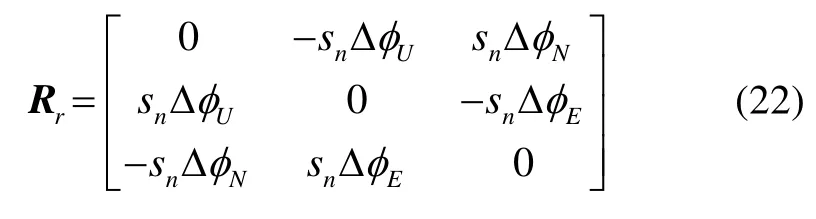
1.3 Measurement model

As for velocity matching, the measurement equation is:

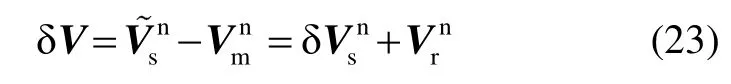
As for angular rate matching, the measurement equation is derived as follows:

2 Design of transfer alignment filter

According to the formulas derived above, the filter can be designed as:

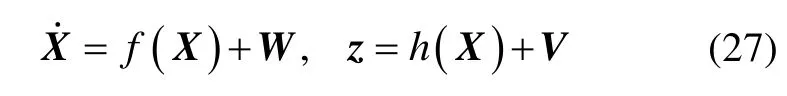
Where Xis the system state vector,fis the system nonlinear function, Wis the system process noise vector, z is the measurement vector, his the measurement function, Vis the measurement noise vector. Here the velocity error, rotation vector error, constant biases of accelerometers and gyros are chosen as the states to be estimated, which are described as:

Furthermore, the system nonlinear function and the measurement function of the transfer alignment filter are:

Since there are rounding errors existing in numerical calculation of UKF, it will damage the estimation error covariance matrix’s non-negative definite and symmetry, and therefore it will affect convergence stability of the filter. To deal with this problem, squareroot unscented Kalman filter is used in the TA to guarantee numerical stability and positive semi-definiteness of the state covariance. SRUKF forms of the UKF make use of three powerful linear algebra techniques, QR decomposition, Cholesky factor updating and efficient least squares. The SR-UKF implementation is as follows and uses the following variable definitions:

1) The constant α determines the spread of the sigma points aroundand is usually set as: 0.0001≤α≤1;

2) β is used to incorporate prior knowledge of the distribution of x, hereβ=2;

Sigma point calculation and time update:

Measurement update equations:

State update equations:

3 Simulation

3.1 Simulation conditions

To simulate the estimation of the misalignment in shipboard environment, the following simulation condition has been setup. It is assumed that the lever arm effect and flexure deformation have already been compensated. The MINS is of high accuracy and considered to have no errors. Assume that the ship sways around the pitch, roll, yaw axis with sinusoidal motion just as formula (36),

Where,θm,γmandψmare the amplitudes of the sway. ωi=2π/Ti(i=p,r,y), here Tiis the period of sways. The values of the corresponding variables are defined in Table 1[13]. The linear motion and error parameters of the sensors are respectively defined in Table 2 and Table 3. Here the sampling period is 0.005 s and the filtering period is 0.01 s.

Tab.1 Sea condition

Tab.2 Linear motion

Tab.3 Sensor error elements of the SINS

Suppose the initial misalignment errors on E, N, and U are 0.5°, 0.5° and 10°, respectively.

3.2 Simulation results

The strapdown INS velocity and attitude error propagation model based on the phi angle approach is the most common way to deal with large initial attitude errors[4]. Here, we compare the RVE model with the nonlinear phi angle (NPA) model proposed in [6]. As the horizontal misalignment angles are small, they can be estimated quickly and accurately with the two models. Table 4 shows the azimuth misalignment estimation errors in different initial azimuth misalignment conditions. It can be seen that the large initial azimuth misalignment is estimated more accurately by using the RVE model than the NPA model. So the RVE model is a better choice to finish the TA of shipborne aircraft.

Tab.4 Azimuth misalignment angle estimation errors in different initial misalignment conditions

As the calculation of Jacobian matrices based on the rotation vector error model is very complicated and the counting amount is huge, here we do not consider about the EKF. Fig.1 shows the estimation error with large misalignment by using UKF method and SRUKF method.

Fig.1 Estimation errors of the misalignment angles based on UKF and SRUKF

It can be seen that the two nonlinear filters both can achieve stable state at 10 s. And the alignment accuracy based on the two methods is nearly the same. However, the numerical stability can be improved and also thepositive semi-definiteness of covariance matrices can usually be guaranteed with the SRUKF. Furthermore, the SRUKF can meet the requirement of accurate and rapid initial alignment of shipborne aircrafts, and also guarantee the numerical stability. So the SRUKF is better than that of UKF in the transfer alignment.

Fig.2-Fig.7 shows the standard deviation estimation (SDE) of the rotation vector errors in different conditions. Tab.5 makes a list of the average standard deviation estimation of rotation vector errors in 30 times simulation.

Fig.2 Standard deviation estimation for rotation vector error of still ship in medium sea condition with velocity matching

Fig.3 Standard deviation estimation for rotation vector error of constant ship in medium sea condition with velocity matching

Fig.4 Standard deviation estimation for rotation vector error of accelerating ship in medium sea condition with velocity matching

Fig.5 Standard deviation estimation for rotation vector error of constant ship in medium sea condition with velocity plus angular rate matching

Fig.6 Standard deviation estimation for rotation vector error of accelerating ship in medium sea condition with velocity plus angular rate matching

Fig.7 Standard deviation estimation for rotation vector error of constant ship in peaceful sea condition with velocity plus angular rate matching

As can be seen in Fig.2 to Fig.4 (corresponding to Tab.5-group I), horizontal rotation vector error with velocity matching can be aligned quickly and accurately. However, the vertical component converges slowly which takes approximately 200 s to achieve the desired accuracy (0.0527°) in the still and constant speed motion. However, the vertical component can be converged faster in accelerative motion as shown in Fig.4 (corresponding to Tab.5-group I-column C). It can be seen that when the ship suddenly accelerates at 20 s, the azimuth misalignment angle is converged in 5 s with the SDE to be 0.0306°. This is because that the maneuver of the ship in a short time improves the observability of the azimuth misalignment angle.

From Fig.5 to Fig.7 (corresponding to Tab.5-group II), it shows that components in three directions can rapidly converge to a high precision with the velocity and angular rate matching. Comparing Fig.5 (corresponding to Tab.5-group II-column A) with Fig.7 (corresponding to Tab.5-group II-column C), we can get that higher accuracy is attainable under more violent swing condition. That is because the observed angular rate is small in the peaceful sea and it will largely affected by the gyro drifts. As a result, the observability of the azimuth misalignment angle will be deduced. The comparison of Tab.5-group I and II shows that the velocity and angular rate matching method is better than that of velocity matching, and can meet the TA requirement of rapidity and accuracy.

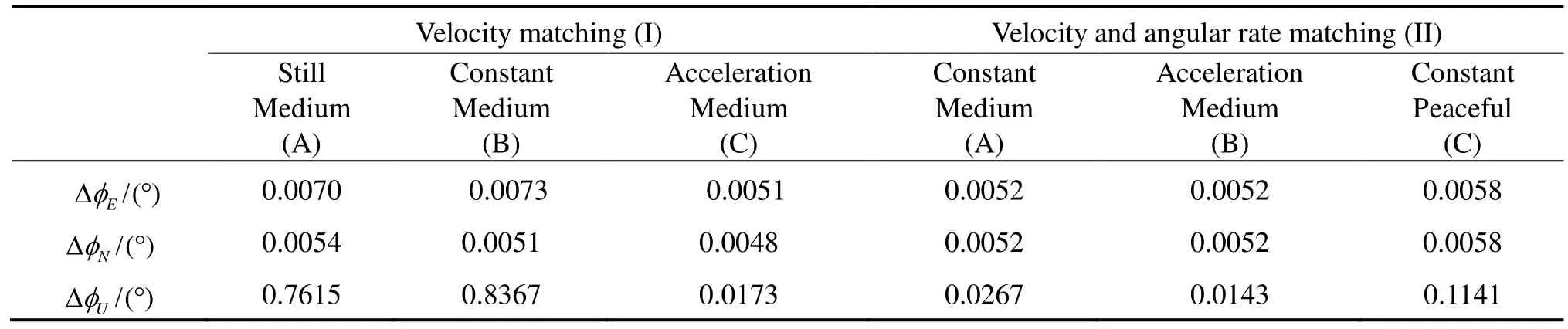
Tab.5 Average standard deviation estimation for rotation vector errors (50 s)

4 Conclusion

To deal with the large misalignment of shipborne aircraft on the carrier, rotation vector error -based nonlinear error equation, measurement model and SRUKF are introduced. Digital simulations are implemented to compare the estimation effect of RVE model with SRUKF under the different sea condition and linear motions. Results demonstrate that velocity and angular rate matching with acceleration motion can achieve the highest alignment accuracy within 10 s. Furthermore, the rotation vector error model has higher accuracy in large heading error estimation than the nonlinear phi angle model. Therefore, in the practical applications, this method can be chosen to complete the TA of shipborne aircrafts’ INS.

[1] Titterton D H, Weston J L. Strapdown inertial navigation technology[C]//2nd edition. USA: AIAA, 2004: 277-301.

[2] Wang Yong-jun, Xu Jing-shuo, Wang Xiao-fei. Improved rapid transfer alignment method for SINS of carrier plane [J]. Journal of Chinese Inertial Technology, 2014, 22(1): 45-50.

[3] Yang Gong-liu, Wang Li-fen, Yuan Er-kai. Rapid transfer alignment of lager misalignment angle for carrier aircrafts [J]. Journal of Chinese Inertial Technology, 2014, 22(5): 597-600.

[4] Lu Yuan, Cheng Xiang-hong. Random misalignment and lever arm vector online estimation in shipborne aircraft transfer alignment[J]. Measurement, 2014: 756-764.

[5] Mao Yu-liang, Chen Jia-bin. Analysis of attitude error models of strapdown inertial navigation system[J]. Journal of Chinese Inertial Technology, 2013, 21(2): 182-185.

[6] Sun Chang-yue, Deng Zheng-long. Alignment of shipborne weapon INS with large initial azimuth uncertainty[J]. Journal of Chinese Inertial Technology, 2008, 16(5): 534-542.

[7] Xiong Zhi-lan, Hao Yan-ling, Sun Feng. Rapid matching alignment algorithm of inertial navigation system based on quaternion[J]. Journal of Harbin Engineering University, 2008, 29 (1): 28-34.

[8] Li Wei, Wang Jin-ling. Effective adaptive kalman filter for MEMS-IMU/Magnetometers integrated attitude and heading reference systems[J]. The Journal of Navigation, 2013, 66: 99-113.

[9] Fang Jiang-cheng, Yang Sheng. Study on innovation adaptive EKF for in-flight alignment of airborne POS[J]. IEEE Transaction on Instrumentation and Measurement, 2011, 60(4): 1378-1388.

[10] Li Jing, Song Ning-fang. Fuzzy adaptive strong trcking scaled unscented kalman fiter for initial alignment of large misalignment angles[J]. Review of Science Instruments, 2016, 87(7): 075118.

[11] Sun Jin, Xu Xiao-Su, Liu Yi-Ting. Initial alignment of large azimuth misalignment angles in SINS based on adaptive UPF[J]. Sensors, 2015, 15: 21807-21823.

[12] JaeHyok K, Mao Xu-chu, Li Shao-yuan. BDS/GPS dual systems positioning based on the modified SR-UKF algorithm[J]. Sensors, 2016, 16: 635.

[13] Liu Xin, Wang Bo, Deng Zhi-hong. Rapid alignment method of INS with large initial azimuth uncertainty under complex dynamic disturbances[C]//Proceeding of the 2012 UKACC International Conference on Control. Cardiff UK, 2012: 1070-1075.

基于旋转矢量误差模型的舰载机大失准角传递对准技术

汪湛清1，李丽华1，刘 昕2，张延顺3

（1. 北京理工大学 自动化学院，北京 100081；2. 沈阳航空航天大学 航空航天学部 探测制导与控制技术实验室，沈阳 110136；3. 北京航空航天大学 仪器科学与光电工程学院，北京 100191）

为实现舰载机大方位失准角条件下的快速传递对准，提出采用旋转矢量误差模型。分别推导了速度匹配和速度加角速度匹配的量测模型。为解决非线性滤波器的稳定性和快速性，提出采用平方根无迹卡尔曼滤波SRUKF来估计失准角。仿真结果表明，旋转矢量误差模型相对于非线性的欧拉角误差模型有更高的估计精度。在海况引起的摇摆运动下，运用速度加角速度匹配方法可以在50 s内完成对准，此时水平精度达到20″以内，航向精度达到1′以内。由此表明所提出的算法可以满足舰载机传递对准快速性和精确性的要求。

传递对准；舰载机；旋转矢量误差模型；平方根无迹卡尔曼滤波

U666.1

：A

2016-09-13；

：2016-11-26

“十二五”装备预研项目（51309040604）

汪湛清（1968—），女，高级工程师，从事嵌入式系统，组合导航与智能导航研究。E-mail: wangzq@bit.edu.cn

1005-6734(2016)06-0723-07

10.13695/j.cnki.12-1222/o3.2016.06.005