《新课标》与《义教版》分数应用题教学异同的实践与研究

诸葛军

【摘要】本人执教六年级多年，今年第一次使用《新课标》教材，对学生进行“用分数解决问题”教学时很发现教学效果很差，联想到两年之内教师还是同一个教师，学生也是同龄的学生，唯一改变的是材。所以笔者试着对《新课标》和《义教版》两种教材进行比较分析，发现这两种教材对分数应用题的编排有较大的差异，从而提出在《新课示》的教材下教学“用分数解决问题”的策略。

【关键词】《新课标》 《义教版》 “分数解决问题” “分数应用题”

【中图分类号】G62 【文献标识码】A 【文章编号】2095-3089（2016）03-0023-03

一、问题的提出

在教学用百分数解决问题（新课标P90例2）时，“例2题目如下：我们原计划造林12公顷，实际造林14公顷，实际造林比计划增加百分之几？”我设想的教学思路是：第一步由分数的简单三类应用题引入，准备题三道①原计划造林120公顷，实际造林是原计划的4/5，实际造林多少公顷？②实际造林120公顷，是原计划的4/5，原计划造林多少公顷？③原计划造林120公顷，实际造林100公顷，实际造林是原计划的几分之几？第二步将分数改成百分数，接着重点教学第三类应用题，从而求让学生回忆求一个数是另一个数的几分之几（百分之几）的应用题的关键在于找出哪两个量相比，第三步引到本节课求一个数比另一个数多（少）百分之几的应用题，也在于找出哪两个量相比，只不过要用多（少）的量和单位“1”相比。

课堂教学片断：

准备题练习五分钟后，师：已经做好的请举手。

生反应：举手的同学寥寥无几。

教师耐着性子再等了片刻，举手的还是那么几位同学，和原来相差无几。

教师循回检查，发现学生解答①②两题的正确率不超过50%。

于是笔者只好调整教学思路，将准备题当着练习课来教学，当教师告诉学生求一个数的几分之几是多少用乘法时，一位平时成绩还较好的女学生怯怯地问了我一句：“老师，为什么求一个数的几分几是多少用乘法？”，听到这一问话，我当时惊呆了，这是最基本的东西，也是第二单元学习的一个重点，这位学生的问话，让人感觉是：这位女生好像从来没有学过分数应用题似的，好像今天是第一节刚接触应用题，（但现实是：用分数解决问题的教学已接近尾声，剩下的教学只不过是百分数的应用而已，而且这还是平时表现比较好的一位女生）分数应用题还是停留在这样的理解基础上，也难怪学生不能正确解答①②类应用题。

二、原因的分析

课后分析：这种情况的出现主要是这几个原因造成的，第一、学生当初在学习“用分数解决问题”时根本就没有很好的掌握这一知识。第二，学生的知识出现了遗忘，而③题正确率较高的原因是由于这段时间学生正在学习百分数的意义和百分率应用题。

再进一步思考，两年前我还是我，学生也是同龄的学生，两年前利用《义教版》教材进行分数应用题教学时一直比较顺利，根本就没有出现过这样的问题，两年后怎么反差如此之大。从而让人想联，这样的问题的出现是不是与新课标的教材有关，笔者用了一个星期的时间将《义教版》教材和《新课标》教材进行了比较，结果发现如下：

《义教版》和《新课标》编排的不同点：

1.数量上比较，义教版这部分应用题共29+31+16+90=166道，新课程共19+13+47=69道，《新课程》从题目数量编排来看，练习题比《义教版》少了一半多，这对于学生技能的形成就少了一道工序。俗话说：“勤能补拙”，作业练习题的减少，这对于还处于形象思维向逻辑思维转化、理解力本来就较差的六年级学生来说，掌握这一类应用题就增加了难度。

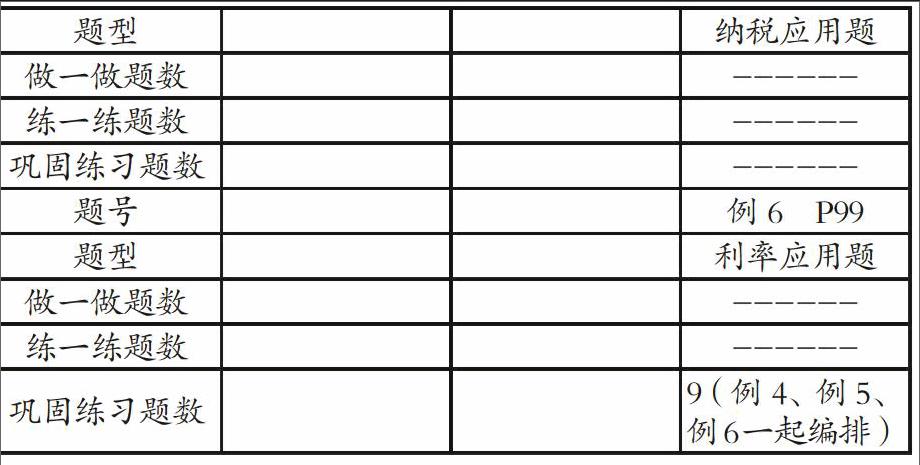
2.编排秩序比较，《义教版》先出现的是百分数应用题，再出现分数乘除应用题，最后出现稍复杂的分数乘除混合应用题。体现了一种由易到难的课程编排理念，比较适合学生的认知规律，掌握起来经比较容易。而《新课程》内容编排以应用为理念，学以致用，学到分数乘法就编入用分数乘法解决问题，进行百分数教学时就编入用百分数解决问题。但这样一来，解决问题的难易度就受到了影响，因为用百分数解决问题相对更容易一些，诸如象税率、利率单位“1”的量是已知的，而分数应用题的真正难点在于求单位“1”的应用题。所以难点应该是第二单元分数除法应用题，这样一来难点就靠前，学生掌握这一部分知识就比较累，正因为这一部分知识没有掌握到位，自然也影响到了后一单元“用百分数解决问题”。

3.难点编排比较，《义教版》的分数应用题的难点是放在第四单元（分数、小数四则运算和应用题）在这一单元里，《义教版》教材前后共安排了90道应用题，这对于学生辨析、区分、理解分数应用题无异有极大的帮助。而《新课标》的难点不是很明确。

三、《新课标》“用分数解决问题教学”的教学策略

策略（一）充分理解分数应用题的内涵和外延。

在进行第二单元（分数乘法）教学时，学生比较容易接受，正确率较高，但学生是否真正理确单位“1”的量，又是另外一回事，所以在进行这一教学环节时，一定要引导学生充分认识单位“1”，要以分析理解为前提，不以学生的作业正确率为唯一指标。让学生真正知道一个数的几分之几的外延和内涵。

策略（二）寻找解答分数应用题的最佳方法。

1.化抽象文字为表象图例。在教学例2“美术兴趣小组有25人，比航模小组多1/4，航模小组多少人？”时，我将教学的重点放在帮助学生理解“比航模小组增加1/4”，在这基础上构画出两者的倍比关系线段图：

有了这样的倍比关系线段图就将原先的抽象文字符号转化成直观形象的图示。这就给解决分数应用题给了很大方便，所以当教师再将已知条件和问题标出后，学生大多能正确计算；

2.优化分数应用题学习的过程。我们学校今年在数学应用题教学时采用了“三想教学法”。一想把谁看成单位“1”；二想数量关系是什么；三想怎样列式；如上段中例2的解题思路为：根据“航模小组增加1/4”把航模小组看作单位“1”（一想）。根据“航模小组增加1/4”转化为航模小组是美术小组的（1+1/4）（二想）。再根据乘法的意义列出方程式或算式（三想）。这种解答思路比较明确，学生比较容易掌握，并运用了对应、转化和代数的数学思想和方法，降低了思维的坡度，对于逻辑思维较差的小学生提供了解题方便。

3.“口诀”明确化。对于思维迟缓的学生则赠送两看口诀“看看单位1，确定乘与除，看看多和少，决定加与减”。有了这两句口诀，思维迟缓的学生也能根据口诀进行仿练，经过长期的训练，这类学生也能掌握分数应用题的解题方法。

策略（三）反复强化，形成动力定型。

巴甫洛夫的“经典条件反射说”和斯金纳的“操作性条件反射说”都将反射和强化作为学习的一个必要过程。斯金纳认为，人和动物的学习行为主要是由操作条件反射构成的，他认为行为之所以发生变化是由于强化作用，强化是塑造行为的有效而重要的条件，所以学生在学生某一个知识点时要及时的“反馈”和强化，从而将这一知识点落到实处（经强化学生能每次都做出正确的反应，使错误率降低限度）。本人认为在进行《新课标》的“用分数解决问题”的教学时，要做好三个强化，第一个强化用在刚进行“用分数解决问题”教学时，这一阶段可以适当增加题目量。（除了《新课标》课本上的习题之外，教师可以自编题目让学生进行练习，最方便最有效的方法是将原来的《义教版》的课本中的题目进行利用） 第二个强化则分解在平时常规的课堂教学中，在平时教学中适时的出几道分数应用题，对这方面知识进化强化。 第三个强化用在进行百分数解决问题教学前，因为这一阶段的教学和“用分数解决问题”是断档的，中间穿插了《圆的认识》教学，对于记忆力差的学生来说，分数应用题已经开始遗忘了，所以在这个时候进行一次完整的分数三类应用题的强化。

参考文献：

[1]邱少华.解应用题的钥匙[M]. 江苏：江苏人民出版.

[2]朱智贤.儿童心理学[M]. 北京：人民教育出版社.

[3]童祥祯.小学数学课堂教学艺术[M]. 北京： 首都师范大学出版社.

[4]程功，陈仙梅.教育心理学[M]. 杭州：浙江大学出版社.