一道全国高中数学联赛不等式题的反证法

胡铭杨（江西省吉安市新干县新干中学）



一道全国高中数学联赛不等式题的反证法

胡铭杨
（江西省吉安市新干县新干中学）

本文旨在针对2015年全国高中数学联赛（A卷）加试中第一题，探讨该不等式证明题的多种解法，给出笔者2015年参赛的个人解法以作为参考。

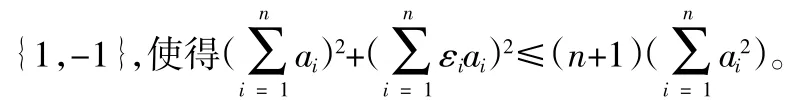
思路：首先，作为一道证明题，我们发现题中所要证明的命题是个存在性命题，正面求证似乎较难突破，我们不妨尝试反证法。

联想竞赛中常见的平均值原理，将其转化为如下命题：

（1）对于ε1，ε2…，εn的每一种对应，记之为Ai（i=1，2，…，2n），显然共有2n种对应。

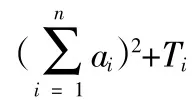
这样，我们通过反证法将原本分散的2n种排列集合成一个整体，省去了特殊情况入手讨论最值的繁难，而是将特殊化为一般。这便是平均值原理的魅力。

有关（4）的证明，观察知每个Ti都可拆开：

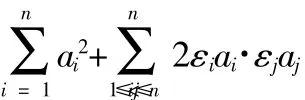
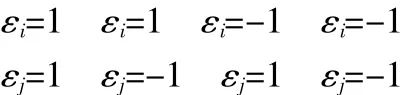
·编辑韩晓