北斗双频组合动对动高精度相对定位新算法
伍劭实,赵修斌,庞春雷,段 荣,仝海波
(空军工程大学 信息与导航学院,西安 710077)
北斗双频组合动对动高精度相对定位新算法
伍劭实,赵修斌,庞春雷,段 荣,仝海波
(空军工程大学 信息与导航学院,西安 710077)
针对动对动相对定位基线矢量实时变化导致整周模糊度浮点解在动态情况下难以快速精确求解的问题,提出了一种北斗双频动对动相对定位算法:对组合双差方程基线向量的系数矩阵进行奇异值分解,并变换组合双差方程以消除基线参量,将变参数估计问题转化为定参数估计问题,然后采用递推最小二乘算法实时推算组合模糊度的浮点解及其协方差矩阵,在此基础上,采用最小二乘模糊度降相关平差法(LAMBDA)搜索和固定组合模糊度。试验结果表明,该方法能够快速准确固定组合模糊度,与单频解算相比,初始化时间用时更短,基线误差在5 cm以内,能较好地适用于动对动相对定位。
北斗导航系统;动对动;奇异值分解;递推最小二乘;双频组合;整周模糊度
动对动高精度相对定位是空中加油、舰载飞机着舰、飞机精密编队飞行等军事应用的核心技术之一,其关键在于动态情况下快速、准确地解算出整周模糊度[1]。当前,一般采用先静态初始化模糊度而后开始运动的方式实现动态高精度相对定位。采用这种方式,一旦发生周跳或卫星信号丢失,就需要静止重新进行初始化,显然在实际军事应用中是不允许的,也就迫切需要寻求模糊度的动态初始化方法。
由于动对动相对定位基线矢量实时变化,使得模糊度浮点解在求解时相比于静态定位更加困难。一般而言,模糊度的浮点解解算可采用最小二乘法、递推最小二乘法、卡尔曼滤波等方法。最小二乘属于批处理算法,计算量大,一般用于对实时性要求不高的静态定位中;递推最小二乘可以实时推算模糊度的浮点解,但其只适用于定参数估计,不能直接用于动对动;卡尔曼滤波对于运动模型的建立要求较高,若状态转移矩阵设计不合理,浮点解的精度就难以满足要求,这将不利于后续的模糊度搜索和固定。 为了满足动态定位对实时性的要求,许多学者尝试从系统模型角度解决这一问题,提出了单历元解算方法,但由于动对动情况下先验信息的局限性,使得单历元解算成功率较低。因此,动对动相对定位始终是国内外研究的热点和难点。
对此,本文从模型和算法两个角度出发尝试解决这一问题,以用于北斗系统动对动相对定位。一方面采用双频组合增强系统模型使得模糊度的求解相比于单频解算更加容易[2],另一方面将奇异值分解和递推最小二乘算法相结合,从而消去基线参数[3-4],将变参数估计问题转化为定参数估计问题,进而达到在动态情况下实时精确推算组合模糊度浮点解及其协方差矩阵的目的,有效实现了模糊度的动态初始化。
1 双频观测量的线性组合
短基线条件下,B1、B2两载波频率上的双差载波相位观测方程分别为

式中:下标“1”“、2”分别表示B1和B2频率;φij为双差载波相位观测量,i、j分别代表第i颗北斗卫星和第j颗北斗卫星;λi(i=1,2)为对应频率的载波波长,l为接收机至卫星的单位矢量;b =(bxbybz)T为基线矢量;Nij为双差整周模糊度; εij为双差测量噪声。
将(1)(2)两式线性组合得到:
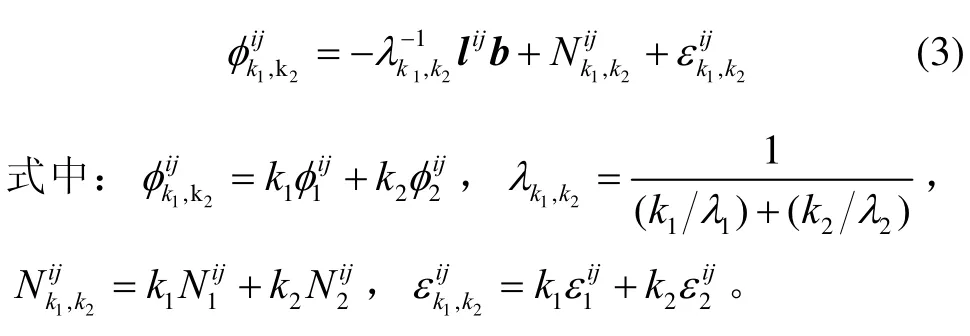
当k1、k2为整数时,也必定是整数。若组合载波波长越长,则相应的组合模糊度也越容易被求解,但由此带来的双差载波相位组合测量值的均方误差也会相应增大[5]。假设 B1、B2两频率的双差载波相位测量值(以周为单位)均方误差互不相关且相等,即σφ1=σφ2=σ,则组合均方误差可表示为

其以m为单位的均方误差为
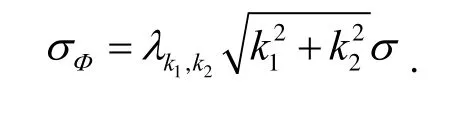
由此可见,应合理选取组合系数k1和k2,使得组合波长尽量长以利于组合模糊度的求解,同时保证组合相位观测量均方误差不至于过大而满足不了相对定位的精度要求。表1给出了经过计算筛选后,波长较长、测量均方误差较小的若干组合。计算时假设σ=0.05。

表1 若干组合观测量的波长及均方误差Tab.1 Wavelengths and mean square errors of several combinations
2 北斗双频动对动高精度相对定位新算法
动对动相对定位时,基线参量b =(bxbybz)T实时变化,随着观测时间的增加,每一历元均会增加3个基线参量,不断变化或者说不断增加的基线参量给问题的求解带来了困难。传统方法是在静态情形下初始化模糊度,当模糊度被正确固定后,其值将不再发生变化,然后即可实现动态相对定位的实时解算[6-7]。由于在实际应用中常常会发生周跳和信号遮挡的情况,在诸如空中加油、飞机精密编队飞行等过程中不可能也不允许再静止下来重新初始化模糊度,因此应考虑模糊度的在航实时解算。对于式(3),考虑将方程中的基线参量消除,采用递推最小二乘算法仅对不随时间改变的模糊度参量实时推算,然后采用LAMBDA算法[8-9]搜索和固定模糊度,从而实现动对动高精度相对定位的实时解算。
2.1 基于奇异值分解的消参方法
假设在m时刻观测到n颗北斗卫星,则根据式(3)可组成n-1个组合双差方程,写成矩阵形式为

式中:


式中:U为(n-1)×(n-1)酉矩阵,V为3×3酉矩阵,∑=diag(σ1,σ2,…,σr),σi(i=1,2,…,r)为矩阵Am的全部非零奇异值。将U分块得到:


由于U为酉矩阵,因此:


式(9)为经过奇异值变换消参后得到的新的组合双差方程,新方程中仅剩下不随时间变化的模糊度参量,此时原来的变参数求解问题转变为定参数求解问题,可采用递推最小二乘实时推算模糊度浮点解及其协方差矩阵。
2.2 基于递推最小二乘的模糊度浮点解实时递推
引理:若A、C、A+BCD均为非奇异方阵,则有如下等式成立:

根据式(9),将前m个历元经过奇异值分解消参后得到的组合双差方程联立:



通过式(13)和式(14)可以实时递推模糊度的浮点解及其协方差矩阵。
2.3 组合模糊度的搜索与固定
得到组合模糊度浮点解N~及其协方差矩阵P之后,可采用LAMBDA算法搜索和固定组合模糊度。
首先建立目标函数[10]:


即可得到组合模糊度最优估计值。
3 试验与分析
在进行实测数据试验的时候发现,当组合测量值的均方误差被放大到大于0.25倍波长以后,组合模糊度浮点解的精度会降低,甚至导致难以固定正确的组合模糊度。根据表1综合考虑组合波长以及组合后的测量均方误差,选择(1,-1)组合进行试验和分析。
3.1 试验条件
为验证本文所提算法的效果,采用基线长度固定情况下动态试验的方法。数据采集时间为 2014年 6月15日20:30,试验地点为学院足球场,两接收机板卡型号均为司南K501,均连接GPS-702-GG型号的双频天线,数据采样率为1 Hz,两天线固定于已知长度的基线两端,并放置于小车前端。试验前测得基线长为3.468 m,取卫星截止高度角为15°,观测到7颗北斗卫星,分别为PRN2、PRN3、PRN5、PRN6、PRN8、PRN9、PRN12,选取仰角最高的PRN3作为参考卫星。先静止观测一段时间,试验将以此作为动态解算的参考,然后绕操场运动,速度约为3 m/s。
3.2 试验过程
先用传统方法解算出B1和B2单频模糊度,并根据组合关系计算出组合模糊度参考值,然后采用本文算法解算(1,-1)组合模糊度。考虑到短时间内观测量之间的强相关性,选取第1个历元和第50个历元计算模糊度浮点解作为初始值,然后采用递推最小二乘算法向后推算30 s,在此基础上采用LAMBDA算法固定模糊度,结果见表2。以21
N为例(其他模糊度解算情况与之类似),组合模糊度浮点解及其整数解求解情况如图1所示。为了比较双频组合解算与单频解算的效果,采用同样的方法解算B1单频模糊度,同样以21
N为例,其浮点解及整数解求解情况如图2所示。图3为根据组合模糊度反解得到的基线长度及基线误差。图4为根据B1单频模糊度反解得到的基线长度及基线误差。

图1 (1,-1)组合模糊度N12,1-1解算结果Fig.1 CalculatedN21of combined integer ambiguity of (1,-1)

图2 B1单频模糊度N21解算结果Fig.2 CalculatedN21of single-frequency integer ambiguity on B1

图3 (1, -1)组合解算基线长度及误差Fig.3 Baseline length and error calculated through combination of (1,-1)

图4 B1单频解算基线长度及误差Fig.4 Baseline length and error calculated on B1
3.3 结果分析
由表2可知,由本文算法解算得到的(1,-1)动态组合模糊度与参考值一致,说明本文算法能够适用于动态双频测量中;比较图1和图2可知,通过本文算法解算模糊度浮点解,其推算过程较为平稳,B1单频模糊度固定正确用时为97 s,组合模糊度固定正确用时为83 s,要稍快于单频解算;由图3和图4可知,基线长度解算结果与试验前所测结果基本一致,但单频解算精度更高,误差为1 cm,相比之下组合测量结果精度稍差,误差在5 cm以内。
对于一般的动对动相对定位应用,5 cm的相对定位精度基本能够满足要求,此时采用(1,-1)双频组合测量,尽管相比于单频测量,其相对定位精度稍差,但组合模糊度初始化用时更短,更能满足动对动的实时性要求。

表2 (1, -1)组合模糊度参考值及试验值Tab.2 Referenced and experimental values of combined integer ambiguity of (1, -1)
4 结 论
本文提出了北斗双频动对动高精度相对定位算法,采用奇异值分解变换组合双差方程以消除基线参量,将变参数估计问题转化为定参数估计问题;然后采用递推最小二乘实时推算组合模糊度的浮点解及其协方差矩阵,在此基础上利用LAMBDA算法进行组合模糊度的搜索与固定。该算法能够较好地解算动态组合模糊度,相比于单频解算,其模糊度初始化时间更短,基线解算误差在5 cm以内,能够较好地适用于动对动相对定位的应用。
由于双频组合测量时,任一频率上的信号出现问题都会影响整个解算过程,因此双频观测量的完好性问题还需进一步研究。
(References):
[1] Jacek P, Pawel W. Assessment of GPS+Galileo and multifrequency Galileo single-epoch precise positioning with network corrections[J]. GPS Solution, 2014, 18(4): 571-579.
[2] 王德军, 熊永良, 刘宁, 等. 宽巷组合及轨迹约束下的列车在轨动态单历元定位算法[J]. 测绘学报, 2014, 43(2): 131-136. Wang Dejun, Xiong Yong-liang, Liu Ning, et al. Train on track kinematic single epoch positioning algorithm based on wide-lane combination and track constraints[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 131-136.
[3] 段荣, 赵修斌, 庞春雷, 等. 改进的GPS整周模糊度动态快速解算[J]. 华中科技大学学报(自然科学版), 2014, 42(9): 54-58. Duan Rong, Zhao Xiu-bin, Pang Chun-lei, et al. Modified algorithm for GPS rapid integer ambiguity resolution[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014, 42(9): 54-58.
[4] 刘宁, 熊永良, 冯威, 等. 单频GPS动态定位中整周模糊度的一种快速解算方法[J]. 测绘学报, 2013, 42(2): 211-217. Liu Ning, Xiong Yong-liang, Feng Wei, et al. An algorithm for rapid integer ambiguity resolution in single frequency GPS kinematical positioning[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 211-217.
[5] 时小飞, 生仁军, 高成发, 等. 基于宽巷模糊度约束的GPS/BDS 动态相对定位[J]. 东南大学学报(自然科学版), 2013, 43(SupⅡ): 446-450. Shi Xiao-fei, Sheng Ren-jun, Gao Cheng-fa, et al. Dynamic relative positioning of GPS/BDS based on wide lane ambiguity[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(SupⅡ): 446-450.
[6] Chen Wan-tong, Qin Hong-lei. New method for single epoch, single frequency land vehicle attitude determination using low-end GPS receiver[J]. GPS Solution, 2012 (16): 329-338.
[7] Teunissen P J G. Integer least-squares theory for the GNSS compass[J]. Journal of Geodesy, 2010, 84(7): 433-447.
[8] Teunissen P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70: 65-82.
[9] Wang Bo, Miao Ling-juan, Wang Shun-ting. A constrained LAMBDA method for GPS attitude determination[J]. GPS Solution, 2009(13): 97-107.
[10] Zhou Yang-mei. A new practical approach to GNSS highdimensional ambiguity decorrelation[J]. GPS Solution, 2011, 15(4): 325-331.
New method for Beidou dual-frequency kinematic-to-kinematic relative positioning
WU Shao-shi, ZHAO Xiu-bin, PANG Chun-lei, DUAN Rong, TONG Hai-bo
(Information and Navigation College, Air Force Engineering University, Xi’an 710077, China)
In kinematic-to-kinematic relative positioning, the floating solution of the integer ambiguity is hard to quickly and accurately be solved in dynamic situations due to the baseline vector’s real-time change. To solve this problem, a novel algorithm is proposed for Beidou dual-frequency kinematic-to-kinematic relative positioning. Firstly, the coefficient matrix of the baseline vectors of combined double-differential equations are decomposed by singular value decomposition, and the combined double-differential equations are transformed to eliminate the baseline parameters, so that the variable-parameter estimation problem is transformed into the constant-parameter estimation problem. Then, the floating solution and the covariance matrix of combined double-differential integer ambiguities are deduced in real-time by Recursive Least Square method. Based on this, the combined integer ambiguities are searched and fixed by LAMBDA algorithm. Experiment results show that, compared to single-frequency solution method, the proposed method takes less time, and the baseline error is within 5 cm, showing that it is suitable for applying in high-precision kinematic-to-kinematic relative positioning.
BeiDou navigation satellite system; kinematic to kinematic; singular value decomposition; recursive least square; dual-frequency combination; integer ambiguity
TN967.1
:A
1005-6734(2016)06-0758-05
10.13695/j.cnki.12-1222/o3.2016.06.011

