内部加强帽形结构轴向压缩吸能特性研究

莫易敏　苏　东　石志华　徐　敏

武汉理工大学，武汉，430070



内部加强帽形结构轴向压缩吸能特性研究

莫易敏苏东石志华徐敏

武汉理工大学，武汉，430070

摘要：通过仿真和落锤试验研究了内部加强帽形结构动态压溃时的吸能特性。首先，从理论上分析内部加强对帽形结构吸能特性的影响；然后，根据仿真结果，对内部加强帽型结构的轴向吸能特性进行了分析，并与无内部加强帽形结构进行了对比；最后进行了试验验证。结果表明：通过改变加强结构，帽形结构的轴向压缩稳定性和吸能特性有了很大的提高，且失效现象得到改善，还有利于结构的轻量化。

关键词：内部加强；帽形结构；吸能特性；轻量化

0引言

一直以来，汽车安全受到人们高度重视，汽车碰撞特别是正面碰撞更是关注的焦点。汽车正碰中通过车身的塑性变形来耗散冲击动能，所以设计出具有较高吸能效率的前纵梁十分有意义。由于成本、节能以及环保等方面是有限制的，故不能一味依靠提高吸能结构的材料特性等方法来提高其碰撞安全性。这促使人们不断对原有结构进行改进和优化，通过适当的结构变化改善其吸能性能。帽形结构通过内部加强可以构成一种很好的碰撞吸能结构，内部加强仅仅是将传统的加强结构进行改进，在使用同样多材料的基础上通过改变结构来提高其吸能特性。许多学者对汽车前纵梁的内部加强进行了研究，刘世龄[1]利用弯矩函数列式讨论了有加强条的薄板弯曲问题；高元明[2]对双室双帽薄壁梁轴向压溃性能进行了研究，其研究结果表明，在双帽型结构中间加焊一层加强板能有效提高其吸能特性。杨笠等[3]将原纵梁内部布置的多个加强板减少为一个，提高了纵梁工艺性；余跃等[4]提出一种等强度贴板加强立柱结构；Zarei等[5]对空心和泡沫填充梁的最大吸能和最大比吸能进行了耐撞性优化研究。

综上可知，为提高帽形结构的吸能特性，前人对加强板和填充内部加强都进行过研究，但很少涉及加强板形式的改变，而内部加强形式的变化对整个帽结构的吸能特性有着非常重要的影响。本文从内部加强结构出发，在折叠单元理论[6-10]的基础上分析加强结构对吸能效率的影响，利用有限元仿真和落锤试验进行试验验证，通过对内部加强结构的优化和设计，提高帽形结构的吸能特性，同时为内部加强结构的设计提供一定的参考依据。

1理论说明

根据Wirzbicki和Abramowicz等给出的理想化机构和分析[6-10]可知，产生轴向压溃的薄壁梁由若干个变形梁单元(super-beam element，SBE)组成，一个梁单元又包括若干个折叠单元(super-folding element，SFE)。划分方法如图1所示[11]。

图1　薄壁梁轴向压溃下的SBE和SFE

在此基础上，对一个折叠单元进行分析，基于对压溃过程的观察，将典型的褶皱发生顺序表示在图2中，它表示了1/4截面的变形过程。这个单元由两种类型的塑性铰组成：水平固定铰(AC、CD)及倾斜移行铰(KC、CG)，倾斜移行铰之间的夹角随着变形的发展而减小。

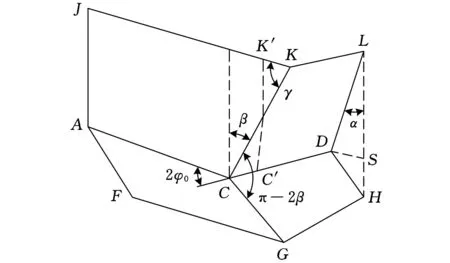
图2　基本褶皱结构几何模型

折叠单元在变形过程中的平均压溃力理论公式[2,12]可以表示为

(1)

(2)

式中，h为板厚；c为SFE单元两边长度AC与CD之和；M0为单位长度的塑性极限弯矩；A1、A2、A3为与折叠单元数目n相关的函数。

I1(φ0)、I3(φ0)的表达式为

(3)

(4)

在式(3)、式(4)中，φ0、α、β、γ所表示的物理意义如图2所示。α、β、γ是折叠单元在变形时的一个过程量。所以平均压溃力的表达式可以写成如下形式：

Fm=f(n,φ0,c,h)

(5)

即平均压溃力是与SFE个数n 、角度φ0、截面边长c、板厚h相关的函数。而在对加强板的研究中将主要考虑截面内折叠单元数目对帽形结构吸能特性的影响。即对内部加强板的设计也主要从截面内的折叠单元数目n入手。

2内部加强帽形结构几何模型

2.1帽形结构

仿真试验所研究的帽形结构为单帽和双帽两种结构。帽形梁因其加工工艺简单等特点在汽车工业中得到了广泛的应用。帽形结构梁通常由金属板焊接而成，其截面形状如图3所示。

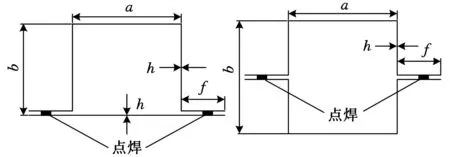
(a)单帽(b)双帽图3　截面几何形状

试验中为了保证试验的一致性，所有单帽和双帽结构的截面尺寸相同。样件的板材厚度h=1.4 mm，尺寸a=b=85 mm，焊接边宽度f=22.5 mm，样件的高度均为400 mm；试验中为保证帽形结构从顶部开始变形，每个样件顶端均设置了腰形诱导槽，诱导槽的尺寸为70 mm×20 mm，诱导槽中心距顶端距离为35 mm。所有样件的材料均为B280VK。

试验中，焊点的布置对结果有较大的影响[13]， 为有效控制焊点对仿真试验的影响，模型建立过程中对其分布方式、间距进行严格的控制[14]，所有样件的焊点布置相同且焊点均位于焊接边的中心处。具体来讲，相邻焊点的间距为30 mm，第一个焊点距离顶端的距离为10 mm。而在样件的加工制作过程中也需严格控制焊点质量。

2.2内部加强结构

研究过程中，对内部加强结构的设计思路主要根据折叠单元理论出发，通过增加截面折叠单元数量(式(5))将传统单腔体截面改进为多腔体截面，为了保证实际加工工艺的可行性并对成本进行控制，在所设计结构装配中，都可以通过简单的点焊连接工艺实现。

研究帽形结构内部加强的主要方法是在基本单帽和双帽截面中加入加强板。仿真中用到的内部加强结构如图4所示。

3仿真分析

在利用有限元对有内部加强的帽形结构进行仿真过程中，用Hypermesh和Ls-Dyna分别对不同的帽形结构进行建模和计算。仿真中，帽形结构的底端固定，另一端受到具有一定速度质量块的刚性体冲击。仿真模型如图5所示。

(a)单帽增加加强结构后的截面

(b)双帽增加加强结构后的截面图4　单帽和双帽加强结构

图5　帽形结构落锤仿真模型

约束底板的全部自由度来模拟落锤试验台的固定工作台，碰撞中的各参数都是根据实际标准设定，本次试验所用碰撞初速度为50 km/h。仿真分析中涉及图4中的8种帽形结构。

空心以及有内部加强的帽形结构动态轴向压缩仿真所得到的力与位移曲线如图6所示。

为了比较内部加强结构给帽形结构带来的影响，图6中对有内部加强和无内部加强帽形结构的力与位移关系进行了比较。仿真中，为了方便比较，在压溃力位移曲线中仅仅取了前200 mm的力-位移曲线，在这段位移中，各梁在压溃过程中压溃力稳定、可比性强。整体来看，有内部加强结构与无内部加强结构相比，初始的最大压溃力增大，而随后的压溃力也在一定程度上有所提高。针对具体单帽和双帽结构，结合图4来看，截面内增加的折叠单元数目越多，压溃力的增加也越明显。

(a)单帽结构

(b)双帽结构图6　帽形结构压溃力与位移曲线

在对力-位移曲线进行比较过后，可以明显看出内部加强对帽形结构的影响。下面将从帽形结构的变形形式进行比较和分析。

增加内部加强前后各帽形结构的变形情况如图7所示。为了比较的一致性，帽形结构的压缩距离均为200 mm。

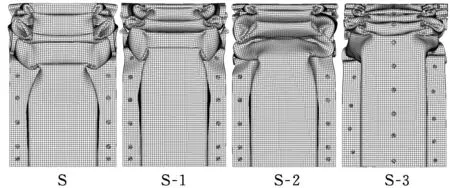
(a)单帽结构

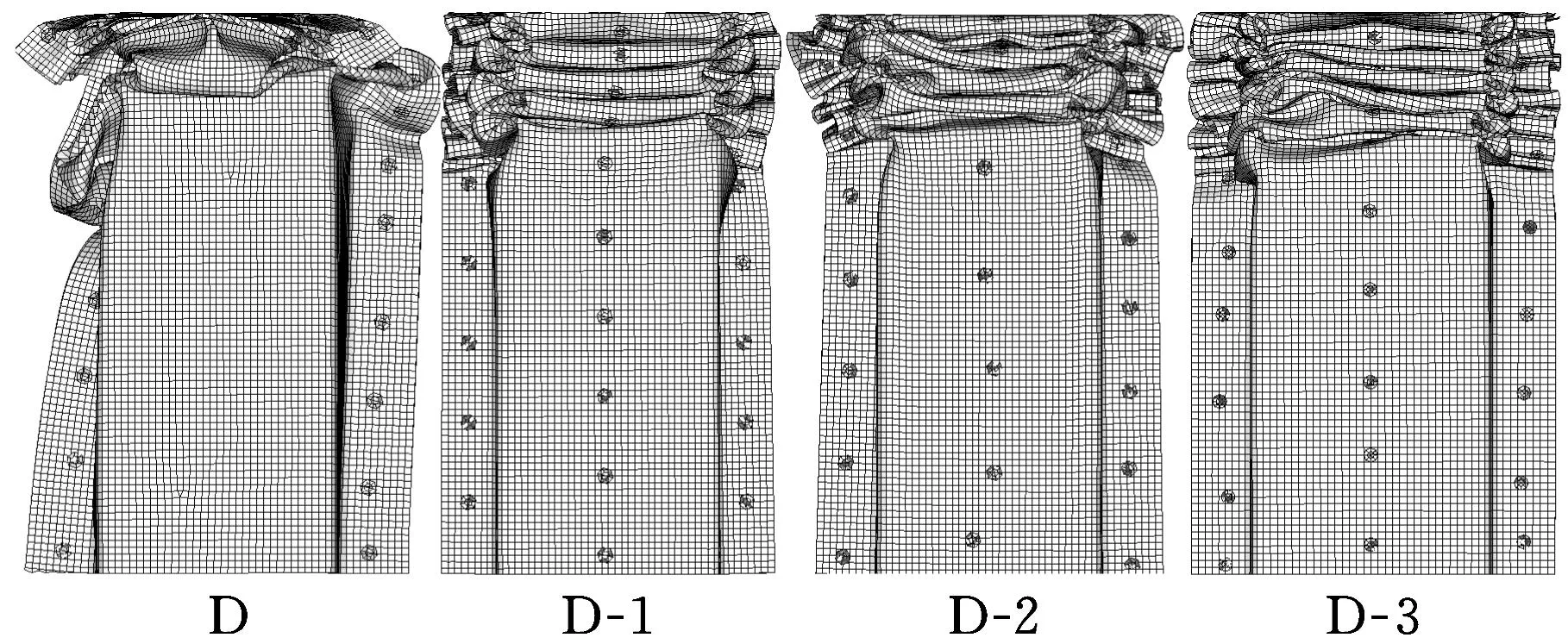
(b)双帽结构图7　帽形结构压缩变形比较

图8　双帽形结构失效现象

由图7可以看出:①单帽系列样件的变形模式为规则的非对称渐进褶皱，没有出现失稳的情况，如图7a所示；②没有内部加强的双帽形样件出现不规则内陷压溃失效现象[13,15]，内陷压溃使结构没有充分地发生折叠变形，降低其吸能效率且容易导致整个梁的失稳，图8为双帽结构D压缩距离为150 mm时的变形图；③所有试件均没有出现焊点开裂、明显弯曲等失效现象。

从变形模式能够看出，有内部加强结构样件与无内部加强结构样件有明显的不同：

(1)有内部加强结构的帽形结构均能发生稳定的轴向渐进压溃变形，且褶皱变形更加规则，特别是双帽结构，大大改善了内陷失效现象，使其变形更加稳定。

(2)通过对图7的观察可以看出，增加内部加强结构以后，在同样的压缩距离内，帽形结构的褶皱数目增加，且更加紧密，说明帽形结构变形半波长明显减小，变形更加充分。

4吸能特性分析

为了具体评价结构的吸能特性，研究人员提出了许多评价指标。本文选择常用的比吸能、平均压溃力这两个主要指标来衡量帽形结构在有无内部加强时吸能特性的变化。

4.1平均压溃力

平均压溃力Fm反映整个吸能过程中冲击力的平均值。它是表征结构吸能特性的重要指标，其定义为

(6)

式中，s为压溃的距离；F(x)为压溃距离为x时的压溃力。

根据式(6)以及仿真所得的力-位移曲线，取s=200mm，便可求出各个样件的平均压溃力。统计结果见表1。

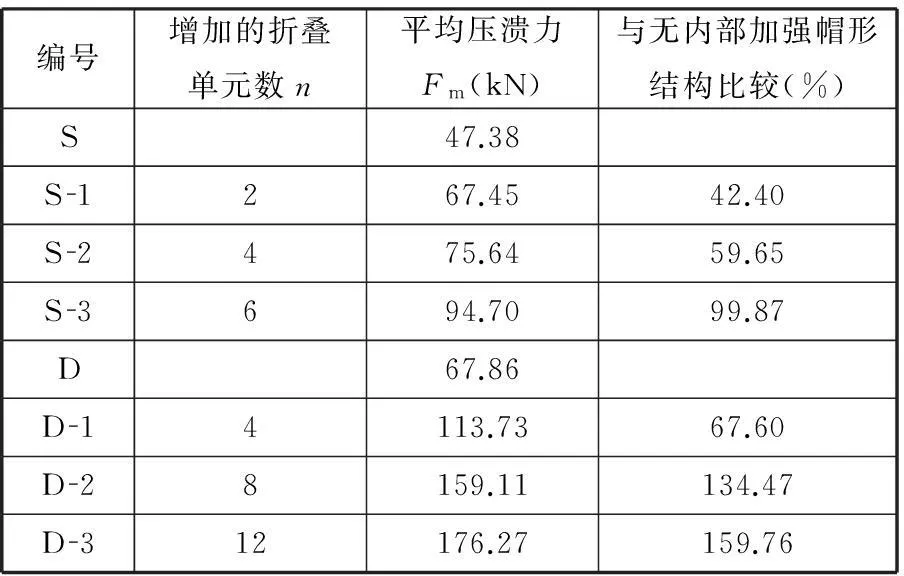
表1　平均压溃力比较

从表1能够看出，与无内部加强结构相比，有内部加强帽形结构的平均压溃力都有一定的提高，这与图6中力-位移曲线反映的情况一致。同时可以看出，截面内每增加一个折叠单元数目，单帽结构压溃力平均增加17.59%，而双帽结构平均压溃力平均增加15.67%。所以内部加强对单帽结构平均压溃力的影响大于对双帽结构平均压溃力的影响。

4.2比吸能

比吸能ASE是指结构(材料)在单位质量下吸收能量的大小，是碰撞吸能过程中材料利用率的度量参数。通常以单位质量所吸收的能量来表征。表达式为

ASE=E/m

(7)

式中，E为压溃过程吸收的总能量；m为参与变形部分的质量。

所有结构均只考虑压缩距离为200 mm时的总吸能值。有无内部加强帽形结构的比吸能结果如表2所示。

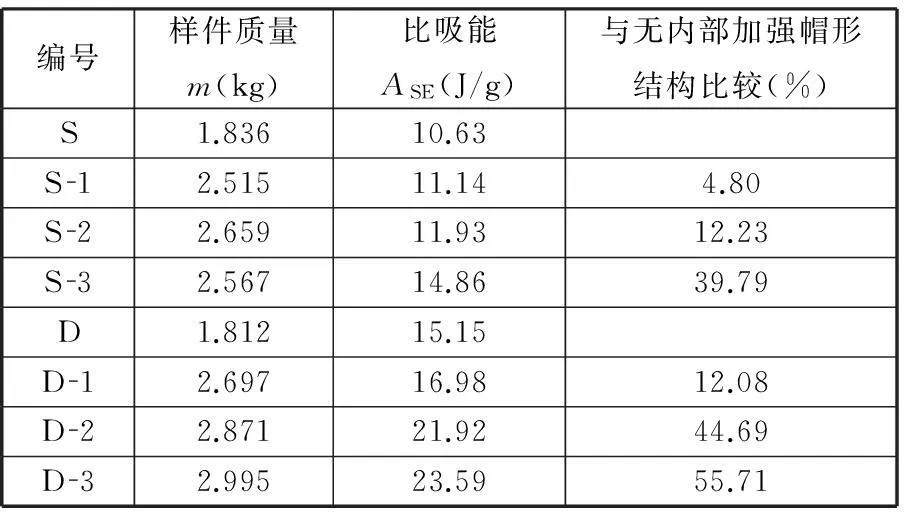
表2　比吸能比较

整体来看，与无内部加强结构相比，有内部加强帽形结构的比吸能都有一定的提高。具体来讲，截面内每增加一个折叠单元数目，单帽结构比吸能平均增加4.03%，而双帽结构比吸能平均增加4.42%。所以内部加强对双帽结构比吸能的影响大于对单帽结构比吸能的影响。显然，在吸收能量相同的情况下，内部加强结构能够减少吸能结构所需要的质量，且内部加强双帽结构所需要的质量最小。这一结论有利于帽形结构的实际工程应用。

5试验验证

针对内部加强对帽形结构轴向压缩吸能特性的研究，对仿真中涉及的8种结构均进行落锤试验，样件的几何尺寸以及材料等均与仿真相同。本试验采用湖南大学土木工程学院自行设计搭建的落锤设备进行试验，落锤下落高度(锤头体面距样件顶端距离)为9.84 m，落锤沿导向柱垂直下落，导向柱上下两端均固定，锤头在接触样件时速度为50 km/h，且锤头质量可以根据具体需要进行调节。采用高采样频率传感器测得锤头加速度及位移曲线，并使用高速摄像设备对样件的压溃变形过程进行记录。样件及试验设备如图9所示。试验得到的各帽形梁的变形结果和力-位移曲线如图10、图11所示。同样没有内部加强的双帽结构会出现仿真中图8所示的内陷失效现象，如图12所示。分析对比各结构压溃结果特征值，如表3所示。

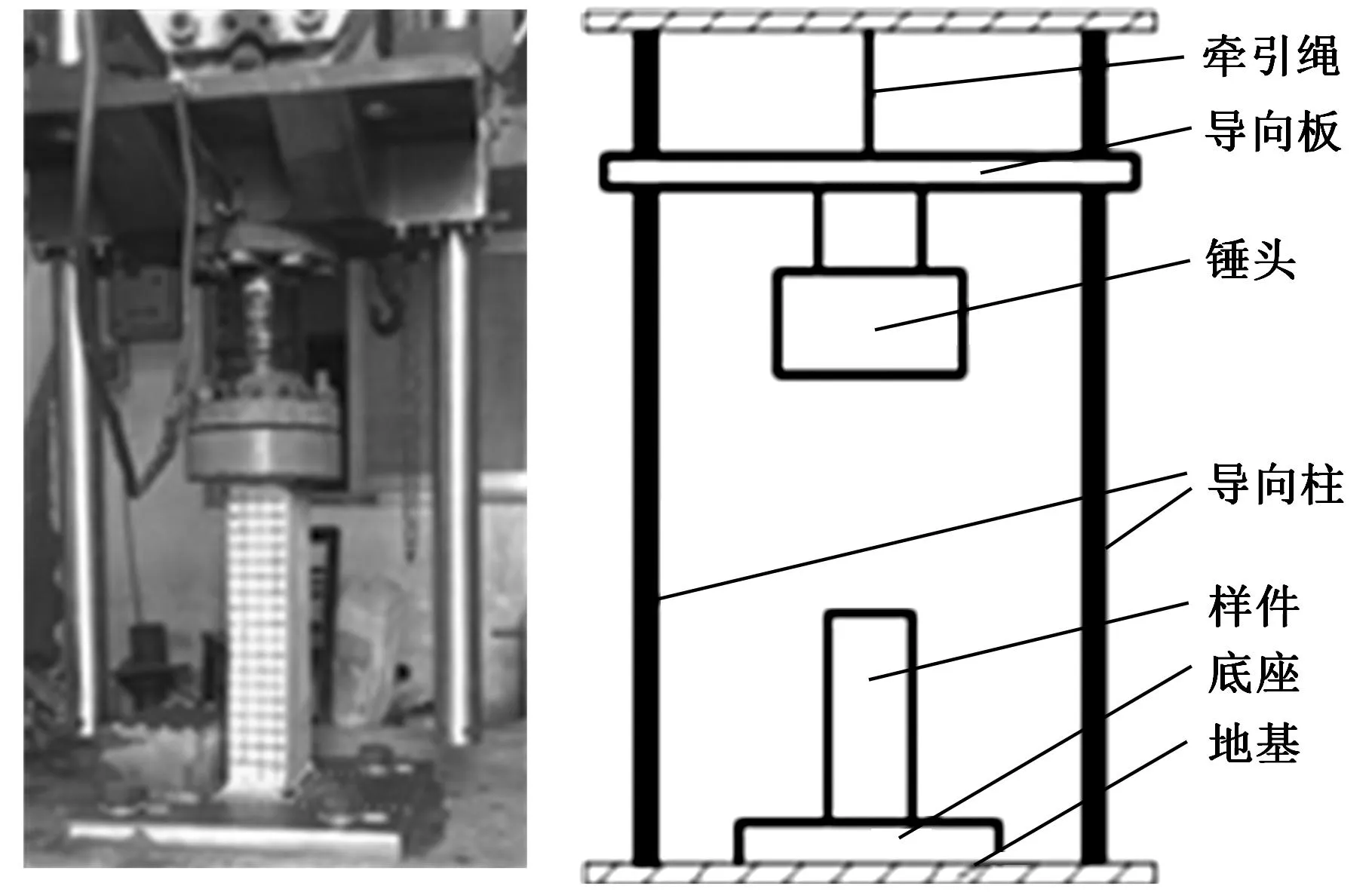
(a)实物照片(b)示意图图9　试验样件及设备

(a)单帽结构试验变形结果

(b)双帽结构试验变形结果图10　变形结果图

(a)单帽结构

(b)双帽结构图11　试验压溃力-位移曲线

图12　内陷失效现象

编号质量m(kg)平均压溃力比吸能Fm(kN)增加率(%)ASE(J/g)增加率(%)S2.0547.549.25S12.6762.3631.179.442.05S22.8678.5065.1210.9818.70S32.75100.11110.5814.3655.24D1.9668.2413.83D12.85120.4776.5416.7120.82D23.02168.04146.2522.2660.95D33.11188.43176.1324.2475.27

对比图10中各结构的试验变形结果可以看出，不管是单帽结构还是双帽结构，在相同压缩距离内，增加截面的SFE数目，帽形梁在压溃阶段内形成的褶皱数目明显增加，且基本单帽、双帽结构的变形形式得到了改善，这与图7中仿真结果所反映的规律相同，验证了仿真规律的正确性；同样对比图6和图11可以看出仿真和试验对截面压溃力的反映基本相同。根据表1、表2、表3，将仿真和试验的关键特征值进行比较可以发现，试验样件的质量整体上大于仿真模型中样件的质量；试验所得截面平均压溃力大于仿真所得压溃力，但是偏差均在8%以内；比吸能方面除了D -2、D -3样件的试验比吸能大于仿真比吸能以外，其余样件试验值均小于仿真值，其中，S、S-1样件偏差达到了15%左右，其余样件的偏差均在10%以内。由此可以说明试验所得结果的特征值与仿真结果的特征值基本吻合。同时从表3可以看出，截面内每增加一个折叠单元数目，单帽结构压溃力平均增加16.77%，比吸能平均增加4.97%；双帽结构平均压溃力平均增加17.36%，比吸能平均增加6.37%。这两项指标与仿真结果是吻合的。

经过对试验结果的分析，可以得出：试验所得结果与仿真结果是相吻合的，仿真所得规律在试验中得到了验证，可以说仿真和试验具有一致性。

6结论

(1)增加内部加强结构以后，将传统的单腔体结构变成多腔体结构，增加了截面内的折叠单元数目，减小了帽形结构的变形半波长、增加了截面褶皱、增加了变形稳定性、明显改善了帽形结构的失效现象。

(2)对比分析吸能和平均压溃力可知，增加内部填充能有效提高帽形结构的吸能特性，且对双帽梁比吸能的改善较明显。

(3)帽形结构截面内的折叠单元数目越多，梁内部结构越复杂，帽形结构的吸能效率就越高。在吸收能量相同的情况下，内部加强结构能够减少吸能结构所需要的质量，这对帽形梁的轻量化以及工程实际应用具有重大意义。

(4)经过对内部加强结构的分析，对帽形结构梁的设计提出了新的指导，同时这一设计方法也可以给其他截面梁内部加强结构的设计提供参考。

参考文献：

[1]刘世龄. 加强板的弯矩函数列式[J]. 计算力学学报, 1999, 16(1)：8-17.

Liu Shilin. Moment Function Formulation of Stiffened Plates[J]. Chinese Journal of Computational Mechanics, 1999, 16(1):8-17.

[2]高元明. 单帽型与双帽型薄壁梁塑性变形特性的简化方法研究[D]. 长春：吉林大学, 2011.

[3]杨笠, 杨延鹏. 微型客车正面耐撞性的结构优化研究[J]. 汽车工业研究, 2014(9):54-57.

Yang Li, Yang Yanpeng. Structural Optimization of Frontal Impact of a Minibus[J]. Auto Industry Research, 2014(9):54-57.

[4]余跃, 周鸿波, 童水光,等. 一种薄壁梁加强结构及其动态抗弯性能分析[J]. 机械科学与技术, 2011, 28(3):80-84.

Yu Yue, Zhou Hongbo, Tong Shuiguang,et al. A Strengthen Structure of Thin-walled Beams and Analysis of Its Dynamic Bending Performance[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 28(3):80-84.

[5]Zarei H R, Kroger M. Bending Behavior of Empty and Form-filled Beams: Structural Optimization[J]. Int. J. Impact. Engng., 2008,35(6)：521-529.

[6]Abramowicz W. Simplified Crushing Analysis of Thin-walled Columns and Beams[J]. Rozprawy Inzynierskie, 1981, 29(1)：5-26.

[7]Wierzbicki T, Abramowicz W. On the Crushing Mechanics of Thin Walled Structures[J]. Journal of Applied Mechanics, 1983, 50(4):727-734.

[8]Abramowicz W, Jones N. Dynamic Axial Crushing of Square Tubes[J]. International Journal of Impact Engineering, 1984, 2(2)：179-208.

[9]Abramowicz W, Wierzbicki T. Axial Crushing of Multi-corner Sheet Metal Columns[J]. Journal of Applied Mechanics, 1989, 56(1)：113-120.

[10]White D, Jonse N, Abramowicz W. A Theoretical Analysis for the Quasi-static Axial Crushing of Top-hat and Double-hat Thin-walled Sections[J]. International Journal of Mechanical Sciences, 1999, 41(2)：209-233.

[11]吴晓杰, 胡宏勋, 刘学军,等. 薄壁梁轴向压溃力的影响参数[J]. 机械设计与研究, 2012, 28(1)：42-45.

Wu Xiaojie, Hu Hongxun, Liu Xuejun, et al. Study of Design Parameters Influencing the Axial Folding Force of Thin-welled Columns Based on VCS Models[J]. Machine Design and Research, 2012, 28(1)：42-45.

[12]余同希, 卢国兴. 材料与结构的能量吸收[M]. 北京：化学工业出版社, 2006.

[13]White M D, Jones N. Experimental Quasi-static Axial Crushing of Top-hat and Double-hat Thin-walled Sections[J]. International Journal of Mechanical Sciences, 1999, 41(2):178-208.

[14]解跃青, 方瑞华, 雷雨成. 基于碰撞数值模拟的汽车纵梁焊点布置方法[J]. 焊接学报, 2003, 24(1)：73-77.

Xie Yueqing, Fang Ruihua, Lei Yucheng. Distribution Method of Welding Spot on Automobile Girder Using Crash Simulation[J]. Transactions of the China Welding Institution, 2003, 24(1)：73-76.

[15]Wu Xueyun, Xia Yong, Zhou Qing. Influence of Flange Location on Axial Deformation Stability of Double-hat Structure[J]. Journal of Beijing Institute of Technology, 2012, 21(1):41-49.

(编辑袁兴玲)

Research on Axial Cushing Behaviors of Inner Stiffened Hat-section Structure

Mo YiminSu DongShi ZhihuaXu Min

Wuhan University of Technology,Wuhan,430070

Abstract：Dynamic axial compression simulation and drop-weight tests were carried out to study the crushing behaviors of inner stiffened hat section structure. First, the influences of inner stiffening on the hat-section structure were analyzed in theory; then, according to simulation results and experimental verification, the crushing behaviors of the inner stiffened hat-sections structure were analyzed. It is found that inner stiffening can greatly increase the energy absorption abilities of the hat-section structure, it is good for failure phenomena, stability and lightweight.

Key words：inner stiffening; hat-section structure; cushing behavior; lightweight

作者简介：莫易敏，男，1960年生。武汉理工大学机电工程学院教授、博士研究生导师。主要研究方向为汽车安全、机电一体化、摩擦学、表面工程学。发表论文60余篇。苏东(通信作者)，男，1988年生。武汉理工大学机电工程学院硕士研究生。石志华，男，1991年生。武汉理工大学机电工程学院硕士研究生。徐敏，女，1992年生。武汉理工大学机电工程学院硕士研究生。

中图分类号：U463.83

DOI：10.3969/j.issn.1004-132X.2016.05.024

收稿日期：2015-05-05