关于试题评价与命制的一点思考
☉江南大学附属实验中学 钱云祥
关于试题评价与命制的一点思考
☉江南大学附属实验中学钱云祥
一、问题来由
在一次网络教研中,有教师提出一个问题:下面这道题有几个解?
如图1,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB的度数为___________.
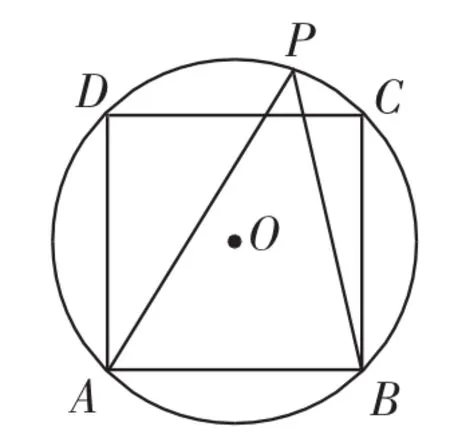
图1

图2
关于这一问题,有的教师认为是一解,有的教师认为是两解.观点一的理由为:“如图”本身也是一个重要的条件,不可忽视;观点二的理由为:题目所给的只是示意图,其中,点P的位置是不确定的,所以点P也可能在上(如图2所示),所以应该有两解(45°或135°).看到上述观点,不少教师感同身受地叹起了苦经:这两种观点似乎都有道理,确实让人纠结,到底是让学生写一解还是写两解呢?甚至还有教师抱怨:现在的学生确实够差的,既不会好好审题,也不会分类讨论,就算明确告诉了本题到底是几解,他们下次还是记不住的.这就不由得我们来深入思考:上述观点,孰对孰错?
二、问题剖析
对于上述疑惑,如果教师自身不能厘清,那么又如何组织教学?为此,我们有必要弄清问题的焦点到底在哪儿,弄清问题的答案究竟如何.
其实,只要仔细推敲题目,即可发现问题所在——这道题目本身表述不够精准.关于“点P在⊙O上”这一条件,既可用静态观点解读为“P为⊙O上某一点”,也可用动态观点解读为“P为⊙O上的一个动点”.两种不同的理解,自然导致出现两种不同的答案.进一步分析,如果把点P理解为⊙O上的一个动点,那么当点P与点A或点B重合时,∠APB就不存在了,更谈不上求∠APB的度数了.由此可见,试题命制不够严谨,容易出现不同理解.这样明显有瑕疵的题目,我们本来就不该随意使用.
三、深层思考
对于如上所述的有瑕疵的题目,难道需要我们的学生去揣度命题者的命题意图吗?答案显然是否定的.基于这样的思考,我们还有必要去纠结到底是一解还是两解吗?我们还有理由去抱怨我们的学生不会审题、不会分类讨论吗?
1.少一点纠结,多一分严谨
围绕这道题的核心价值去分析,题目命制还是很有创意的.我们不妨以图1为例进行分析:要求∠APB的度数,考虑到∠APB是所对的圆周角,而所对的圆心角是∠AOB,因此需连接OA、OB(如图3所示),再由“⊙O是正方形ABCD的外接圆”可得∠AOB=90°,故由圆周角定理可得∠APB=45°.所以说,整道题编排非常巧妙,但却存在前文所述的瑕疵或者说漏洞,因此在弃之可惜的情况下,我们不妨少一点纠结,多一分严谨——对题目加以改进,以使问题没有歧义.

图3
修改理由:文字条件与实际图形相匹配,答案唯一,为45°.所考查的知识点有:正方形的性质、圆周角定理.
方案2:如图4,⊙O是正方形ABCD的外接圆,P为⊙O上异于A、B的一个动点,则∠APB的度数为_______.

图4
修改理由:“P为⊙O上异于A、B的一个动点”,这一条件有两层意思:一是强调P为⊙O上的动点,同时点P在图4中不予标出,这样更显其任意性;二是点P异于A、B,即不与点A、点B重合,这样就排除了∠APB不存在的情形,从而使得问题设置更为严密.毫无疑义,这样修改后,答案为45°或135°.除了方案1所考查的知识点,还考查了学生运动的观点及分类讨论的数学思想与方法.
对照上述两种修改方案,显然方案1比方案2来得简单,到底采用何种方案,需根据学生的学习基础及考查目标来确定.无论是哪种方案,与原题相比,都剔除了含糊的成分,学生不再需要去揣度命题者的命题意图.这样的试题,更显大气.换句话说,难题也要难得在理,我们毫无必要玩文字游戏刁难学生.
2.少一点抱怨,多一分宽容
在网络信息时代,在日常教学中,从实际操作层面上看,不少教师难免采用拿来主义,直接选用现成的资源.比如,在未对每道题深入剖析的情况下,选用了带有瑕疵的题目,那么当面对多样的答案之时,教师又该如何应对?笔者认为,不妨少一点抱怨,多一分宽容——解放思想,允许多样性解读.
我们不妨还是以前面的题目为例,关于此题的答案是一解还是两解,我们大可宽容一点对学生的解答进行评价:“一解(45°)”“两解(45°或135°)”甚至“三解(45°或135°或不存在)”都评判为正确,毕竟每种理解都有一定的道理.允许多样的答案又何妨?题目本身存在的瑕疵性问题,不该让学生来买单.没道理的抱怨只会让学生更加失去学习的信心,宽容并不代表没有原则,适度的宽容反而更能激活学生的思维,唤醒学生参与的自觉.
四、题外话
日常教学中,面对一道道试题,假如我们能有敏锐的眼光去甄别,那么就能减少许多不必要的纠结与抱怨,替而代之的则是以严谨的态度修改完善题目,以宽容之心理解学生.其实,这也是严于律己、宽以待人的一种外在表现.
1.严谨与求实:数学教师理应恪守的态度
作为数学教育工作者,无论是在课堂上,还是在课堂外,我们都应该恪守严谨与求实的治学态度.一方面,我们要敢于对有瑕疵的题目说不;另一方面,我们也不应该人为地把简单问题复杂化.例如,对于下面这道题,我们有必要去分类讨论吗?

图5
如图5,在△ABC中,AB=AC, BD⊥AC于点D,若∠ABD=20°,则∠C=_______°.

严谨是一种态度,有瑕疵不该回避,没问题也不该故意找茬,这就是一种求实的精神.
2.宽容与善意:为人处世必须遵循的准则
宽容犹如一个微笑,一甜到底;宽容犹如一缕清风,沁人心扉;宽容犹如一丝阳光,温暖人心.我们的每一个教育对象都是一个活生生的个体,因此,教师命题应该学会换位思考,充分考虑学生的感受.在命题过程中不宜片面追求难度,更不能用含糊其辞的表述去造成学生理解上的“失误”,而应合理控制难度,清晰表述问题,必要时甚至不妨进行一些善意的提醒.其实,宽容与善意,又何尝不是为人处世必须遵循的准则呢?我们不妨以下面这道题为例说明.
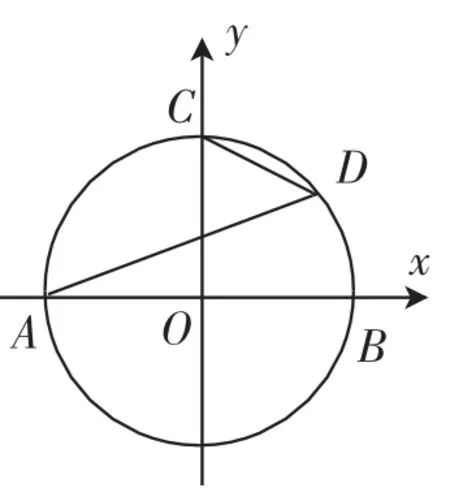
图6
(2011年无锡市中考试卷,第18题)如图6,以原点O为圆心的圆交x轴于A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=20°,则∠OCD=_______°.
题中明确告知“D为第一象限内⊙O上的一点”,这样就排除了点D落在第四象限的可能(由∠DAB=20°可知点D可能在第一象限,也可能在第四象限).这样表述,既降低了试题的难度,也使得图形条件与文字条件相吻合.否则,极易造成一般学生得一解而优秀学生却纠结的结果.
宽容与善意的另一层意思就是不要一味地苛求别人,要知道自己去做很可能远不如别人.智者千虑,必有一失.因此,当其他教师所命制的试题出现一点瑕疵之时,我们应该正确对待.对于由于工作经验的欠缺而造成的一些命题失误,千万不要随意冠之以“学科素养不行”的大帽子.善意的提醒,真诚的帮助,将会赢得别人的尊重.
五、结束语
命题常常需要创新,如果过于束手束脚,那么必将难以有新的突破.探索中求真知,纠错中谋发展.无论是旁观者还是当局者,只有摆正心态,才能共同把相关工作做好,最终让我们的学生得到最好的发展.
参考文献:
1.徐明悦,王克亮,华云峰,张海军.中考命题历险记[J].中学数学教学参考(中),2015(8).
2.刘东升.追问“争议错题”,思辨“认识封闭”[J].中学数学(下),2015(7).
3.周玉俊.小题大作话“折叠”[J].中学数学(下),2015(10).

