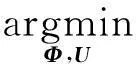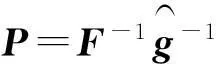基于观测矩阵优化的自适应压缩宽带频谱感知*

王志文，徐以涛，黄鑫权，赵　勇，林　刚

(解放军理工大学 通信工程学院，江苏 南京 210007)



基于观测矩阵优化的自适应压缩宽带频谱感知*

王志文，徐以涛，黄鑫权，赵勇，林刚

(解放军理工大学 通信工程学院，江苏 南京 210007)

摘要：压缩采样(CS，又称压缩感知)技术的出现为频谱感知在更宽的频谱范围探测稀疏信号带来了革命性的契机。这里将观测矩阵优化与压缩采样自适应过程相结合，提出了一种优化的自适应压缩宽带频谱感知算法。此外，还引入交叉验证理论，从而保证了信号采样阶段的自动终止，以防止浪费硬件资源。理论分析和实验仿真表明，相比于传统自适应压缩感知方法，所提算法能够在较低信号采样率的情况下获得满意的信号恢复精度。

关键词：认知无线电；宽带频谱感知；自适应压缩采样；观测矩阵优化

0引言

随着无线通信需求的剧烈增长，频谱资源的匮乏变得越来越严重。然而，众多关于无线电频谱占用的研究已经表明，传统的静态频谱分配策略是造成频谱利用率低下的重要原因[1]。认知无线电的出现为探索频谱空穴的机会利用进而提高频谱利用率带来了契机，而这种能力的实现得益于频谱感知的技术支撑。因此，在宽频带范围内侦查频谱占用情况的宽带频谱感知技术被认为是认知无线电中最为关键的技术，也是极具挑战性的课题之一[2]。

造成上述挑战的原因有很多，其中之一便是接收信号时需要较高的采样率，这就要求接收机拥有复杂且昂贵的模拟数字转换器(ADC)。然而，目前ADC的最高工艺水平仅有3.6 GHz，这并不能满足宽带信号采样的需求[3]。对于宽带认知网络来说，传统的频谱感知方法有极大的局限性。

压缩感知的出现为在数据采集阶段显著降低信号采样率带来了突破性的进展。Tian和Giannakis首次在压缩感知理论的基础上用亚奈奎斯特采样率对宽带信号进行了采样获取[4]。最近，诸如蒸馏感知(DS)[5]等自适应感知技术被证明是一种在噪声环境下有效的信号采集方式。文献[6]提出了序贯压缩感知(SCS)方法，这是一种逐步获得信号压缩测量值的完全自适应的算法。文献[7]通过一种2范数验证的方法在频谱恢复精度达到要求的时候立即使认知终端自动停止信号接收，从而增大了系统的吞吐量。Xing Wang等人还提出了一种基于不同采样率下信道占用信息(CIO)相关性的自适应压缩感知算法[8]。上述算法共同的缺点是在信号的自适应获取过程中缺少观测矩阵的优化，仅靠自适应过程并不能达到最优的采样率。文献[9]设计了一种基于最小Cramer-Rao界的矩阵优化方法，该算法自适应地设计矩阵的行，最终得到最优的观测矩阵。此外，在认知无线网络中动态采样率调整也是一种自适应的压缩频谱感知方法[10]。

在本文中，我们针对宽带频谱感知问题提出了一种优化的自适应压缩采样算法，以期在信号采样阶段选择最优的采样率，避免浪费硬件资源。所提算法通过对观测矩阵进行优化进而提高压缩信号的恢复精度，同时在自适应的过程中引入交叉验证理论来判断停止准则。并且文章已经证明，通过监测交叉验证所产生的恢复误差可以在当前采样率满足需求时及时停止信号获取。

1预备知识

1.1压缩感知理论

在过去，奈奎斯特采样定律是通信和信号处理领域中唯一的采样准则，其避免频谱混叠所利用的先验信息仅为模拟信号的带宽。与此完全相反的是，对于某些稀疏信号压缩感知可使认识用户在低于奈奎斯特采样率的情况下仍然能对模拟信号进行不失真采样。并且实现这种从模拟直接到信息的转换器(AIC)目前已经广泛地应用于压缩频谱感知当中[11]。

考虑一个以奈奎斯特采样率fNyq从射频前端采集下来的信号x∈N×1，其采样时间为τ。此处，令N=τ*fNyq为自然数。通过N×N的基矩阵Θ=[θ1,θ2,…,θN]，我们将x分解成如下形式：

(1)

x=F-1X

(2)

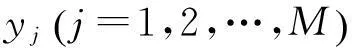
y=Φx=ΦF-1X

(3)

式中，y=[y1,y2,…,yM]T∈M×1表示观测向量，Φ中的元素互相独立且均服从均值为0、方差为1/M的正态分布。因此，在观测矩阵Φ选取合适的情况下，式(2)中的X可以通过解决如下1范数优化问题进行高概率重构：

(4)

在实际的认知无线网络中，不可避免地有噪声的存在，在加性高斯白噪声环境下，压缩感知问题模型改为如下形式：

y=ΦF-1X+n

(5)

式中，n表示测量噪声。此时的信号恢复模型变为：

(6)

式中，ε>0是线性观测存在噪声的情况下信号恢复误差的门限值。

目前，压缩感知的重构算法大致分为两类，一类是凸优化方法，包括基追踪(BP)、梯度投影法(GPSR)等，另一类是贪婪算法，包括正交匹配追踪(OMP)[12]、子空间追踪(SP)等等。本文综合考虑算法速度和实现复杂度，在式(6)的处理上采用OMP算法。

1.2压缩感知中的交叉验证

交叉验证(CV)作为一种统计学上的技术方法，常被用来检验某种模型与它的测量数据是否匹配。在本文中，将交叉验证理论引入压缩感知，用来确定贪婪算法的停止迭代准则。在此，将M×N的观测矩阵Φ拆分为重构矩阵ΦR∈mR×N和校验矩阵ΦCV∈mCV×N，其中M=mR+mCV。因此，交叉验证观测模型可以表述为：

yR=ΦRx+n=ΦRF-1X+n

(7)

yCV=ΦCVx+n=ΦCVF-1X+n

(8)

(9)

根据文献[14]的推导，由εCV估计的信号恢复误差可由如下定理确定，

(10)

式中，h(λ,±)是与λ有关的函数，其定义为：

(11)

erf(u)是正态分布的误差函数，其定义为：

(12)

依据定理1，恢复误差εX的边界最终确定为以下区间，

(13)

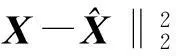
2观测矩阵优化

由于M

(14)

则称矩阵满足K阶RIP条件，其中Ψ=ΦF-1定义为感知矩阵。RIP使得Ψ的任何列之间几乎是正交的，并且保证了Φ和F-1的不相关性。然而，RIP条件的验证非常困难，Michel在文献[15]中给出了一种比式(14)更简洁的表达式：

(15)

式中，μ(Ψ)表示感知矩阵Ψ的相关程度。μ(Ψ)的定义为感知矩阵Ψ所有列之间绝对值最大的归一化内积，即：

式中，φi表示矩阵Ψ的第i列。文献[16]给出了用某一重构算法解决式(6)问题时的均方根误差上界，

(17)

式中，ξ=‖n‖2，δ≥ξ=‖y-ΨX‖2。

由前述可知，相关系数对信号的恢复精度有着显著的影响，也就是说如果感知矩阵Ψ选择合适的话，μ(Ψ)就会充分的小，那么RIP将保证信号高概率地准确恢复。因此，设法降低感知矩阵Ψ各列之间的相关性对提升重构算法性能至关重要。

定义复格拉姆矩阵G=ΨHΨ表示感知矩阵Ψ的相关程度，其中(·)H表示矩阵的共轭转置，那么G中除去主对角元外最大的元素即式(16)中定义的互相关程度μ(Ψ)。格拉姆矩阵的表达式如下：

(18)

(19)

式中，‖·‖F表示Frobenius范数。将G=ΨHΨ=F-1HΦHΦF-1带入式(19)，可得其等价形式：

(20)

文献[17]给出了一种较上式更为简洁的形式，即：

(21)

(22)

文献[18]给出了式(22)的解，即：

Σ=UVH

(23)

式中，U和V可由式(24)进行奇异值分解得到，亦即：

(24)

需要说明的是，此处U是一个M×M的酉矩阵，S是一个M×M的对角矩阵，而V则是一个N×M的半酉矩阵。求得Σ之后，运用最小二乘估计即可得到最优的感知矩阵Φ，其形式如下：

(25)

3优化的自适应压缩宽带频谱感知

为了找到最优的采样率，本节在前述分析的基础上结合交叉验证与观测矩阵优化提出了优化的自适应压缩宽带频谱感知算法。定义压缩采样比R表示系统采样率和奈奎斯特采样的比值，即：

(26)

式中，0

为了简单起见，定义交叉验证均方误差：

(27)

在整个自适应的过程中，前后连续两步mseCV的差值D将作为严格监控的目标，其定义如下：

(28)

在算法运行过程冲，部分参数需要给予特别的关注。步进值Δ可以是0到1之间的任意值，Δ越大，找到最优的压缩采样比R*所需的时间越短，与此同时，算法所找到的R*可能会偏大，造成硬件资源的浪费。改算法中的停止门限D*是另一个需要重视的参数。D*可以设置成非常接近0 的值。若D*太小，尽管算法找了精确的采样率，但是这将消耗过多的采样时间。实际的工程中有时并不需要如此高的精度，因此设置一个适当的门限D*是极其必要的。

4仿真结果

考虑如下宽带信号：

(29)

通过某一无线信道被噪声恶化的宽带信号s(t)其形式变为：

x(t)=s(t)+n(t)

(30)

式中，n(t)是加性高斯白噪声，并通过其方差影响信噪比(SNR)。一个被7 dB噪声恶化的宽带信号如图1(b)所示，这也是仿真试验中待检测的目标频谱。为简单起见，在算法迭代的每一步中设定感知时间τ使得接收信号长度N为固定值，即N=fNyq×τ=1024，其中fNyq=4 GHz。而压缩观测值的数量M=R×fNyq×τ则在算法运行的整个过程中不断地变化。

图1　频谱图

首先验证观测矩阵优化方法的有效性，仿真采用长度N=1 024的宽带信号。此处，压缩采样比R=0.25暂时设置为固定值，噪声变化范围为0～15 dB。为了评估信号重构的效果，定义均方误差(MSE)如下：

(31)

利用OMP算法对信号进行重构的均方误差曲线如图2所示，从中可以看到随着信噪比的增大信号恢复的质量也随之提升，并且采用了优化观测矩阵的重构算法(OMP-OP)性能优于单纯的OMP算法，尤其在低信噪比的情况下更为明显。

图2　OMP和OMP-OP在不同信噪比下的性能比较

图3给出了在不同压缩采样比情况下的信号重构效果，此处设置R的变化范围为0.05到0.9。需要注意的是，在信号采样过程中过小的R将导致很高的重构误差，此时恢复出的信号也是毫无意义的。同样，过大的R则失去了压缩感知的初衷，没有达到节约硬件资源的目的。此处，信噪比设置为5 dB。从图中可以看到，OMP-OP重构性能优于单纯的OMP算法，换言之，在达到同样信号恢复精度的情况下，采用优化观测矩阵的策略将降低所需的采样率。

图3　在不同压缩采样比情况下OMP与

如图4所示，该算法在第9步时检测到D值小于门限0.1，随即找到了最优的压缩采样比R*，此时的精确的压缩采样比为0.45。并且，通过R*采样的信号其频谱重构效果已在图1(c)中给出，从中可以明显的识别出6个主用户的位置。

图4　宽带频谱感知中的算法性能

5结语

文章提出了一种旨在寻找最优压缩采样率以节约硬件资源的宽带频谱感知算法。该算法利用观测矩阵优化的策略得到了在相同条件下比传统压缩感知更低的采样率，同时，文章引入了交叉验证理论使得算法在停止准则满足时自动终止信号采样过程。理论分析和仿真实验均表明，所提算法能够自适应地找到最优压缩采样率，这保证了在有效重构信号的同时最大限度地节约宝贵的硬件资源。

参考文献：

[1]FCC, EtDocket no.02-135, Spectrum Policy Task Force (SPTF) Report. Federal Communications Commission.Tech. Rep.

[2]王志文，徐以涛，江汉等. 基于USRP平台的宽带频谱感知系统设计与实现[J].通信技术,2015,48(06):750-754.

WANG Zhi-wen, XU Yi-tao, JIANG Han, et al. Design and Implementation of Wideband Spectrum Sensing System Based on USRP Platform [J]. Communications Technology, 2015, 48(06):750-754.

[3]Available: http://www.ti.com/product/ADC12D1800.

[4]TIAN Z and Giannakis G B. Compressive Sensing for Wideband Cognitive Radios[C]. in Proc. 2007 IEEE ICASSP, pp, 1357-1360.

[5]Haupt J, Castro R M and Nowak R. Distilled Sensing: Adaptive Sampling for Sparse Detection and Estimation [J].Information Theory, IEEE Transactions on, vol. 57, no. 9, pp. 6222-6235, 2011.

[6]Haupt J, Baraniuk R, Castro R, and Nowak R. Sequentially Designed Compressed Sensing [C]. Statistical Signal Processing Workshop (SSP), 2012 IEEE, Aug., pp. 401-404.

[7]SUN Hong-jian, ZHAO Wei-yu, Nallanathan A. Adaptive Compressive Spectrum Sensing for Wideband Cognitive Radios [J]. Communications Letters, IEEE, vol.16, no.11, pp.1812, 1815, November 2012.

[8]WANG X, GUO W, LU Y, and WANG W. Adaptive Compressive Sampling for Wideband Signal [C]. in Proc. 2011 IEEE International Conference on Vehicular Technology-spring, pp. 1-5.

[9]HUANG Tian-yao, LIU Yi-min, MENG Hua-dong, WANG Xi-qin.Adaptive Compressed Sensing via Minimizing Cramer-Rao Bound [J]. Signal Processing Letters, IEEE , vol.21, no.3, pp.270,274, March 2014.

[10]HUANG Ching-Chun, WANG Li-Chun. Dynamic Sampling Rate Adjustment for Compressive Spectrum Sensing over Cognitive Radio Network [J]. Wireless Communications Letters, IEEE , vol.1, no.2, pp.57,60, April 2012.

[11]Polo Y,WANG Y, Pandharipande A, and Leus G.Compressive Wideband Spectrum Sensing[C]. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) , April 2009.

[12]Davenport M A and Wakin M B. Analysis of Orthogonal Matching Pursuit using the Restricted Isometry Property [J]. IEEE Trans. Inf. Theory, vol. 56, pp. 4395-4401, 2010.

[13]Boufounos P, Duarte M F, Baraniuk R G. Sparse Signal Reconstruction from Noisy Compressive Measurements using Cross Validation[C]. Statistical Signal Processing, 2007. SSP '07. IEEE/SP 14th Workshop on, vol., no., pp.299, 303, 26-29 Aug. 2007.

[14]ZHANG Jin-ye, ZHANG La-ming, Boufounos P T, GU Yuan-tao. On the Theoretical Analysis of Cross Validation in Compressive Sensing[C]. Acoustics, Speech and Signal Processing (ICASSP), 2014 IEEE International Conference on, vol., no., pp.3370, 3374, 4-9 May 2014.

[15]MichaelI E. Optimized Projections for Compressed Densing [J]. IEEE Transactions on Signal Processing, 2007, 55(12):5695-5702.

[16]Donoho D, Elad M, and Temlyakov V N. Stable Recovery of Sparse over Complete Representations in the Presence of Noise [J]. IEEE Trans. Inf. Theory, vol. 52, no. 1, pp. 6-18, 2006.

[17]Stocia P, HE H, and LI J. New Algorithms for Designing Unimodular Sequences with Good Correlation Properties [J]. IEEE Trans. Signal Process., vol. 57, no. 4, pp. 1415-1425, Apr. 2009.

[18]Stocia P, LI J, and ZHU X. Waveform Synthesis for Diversity-based Transmit Beampattern Design [J]. IEEE Trans. Signal Process., vol.56, no. 6, pp. 2593-2598, 2009.

王志文(1991—)，男，硕士研究生，主要研究方向为认知无线电、宽带频谱感知；

徐以涛(1971—)，男，博士，教授，硕士生导师，主要研究方向为软件无线电、认知无线电、无线通信、数字信号处理、通信对抗技术；

黄鑫权(1993—)，男，硕士研究生，主要研究方向为认知无线电、频谱感知安全；

赵勇(1986—)，男，硕士研究生，主要研究方向为认知无线电，通信对抗，移动通信；

林刚(1990—)，男，硕士研究生，主要研究方向为无线通信、频谱预测。

Adaptive Compressive Wideband Spectrum Sensing based on Measurement Matrix Optimization

WANG Zhi-wen, XU Yi-tao, HUANG Xin-quan, ZHAO Yong, LIN Gang

(College of Communication Engineering, PLA University of Science and Technology, Nanjing Jiangsu 210007,China)

Abstract：The emergence of compressive sampling (CS, also known as compressive sensing) technology brings a revolutionary opportunity to spectrum sensing for its detecting the sparse signals in broader spectrum span.In combination of measurement matrix optimization and adaptive process of compressive sampling a modified adaptive compressive wideband spectrum sensing algorithm is proposed.In addition, a CV (Cross Validation) method is introduced, thus to guarantee the automatic termination of signal acquisition stage,and avoid the waste of hardware resources. Theoretical analysis and experimental simulations indicate that, compared with traditional CS recovery algorithm, the proposed algorithm could achieve satisfactory signal recovery precision in the situation of fairly low sampling rate.

Key words：cognitive radio, wideband spectrum sensing, adaptive compressive sampling, measurement matrix optimization

作者简介：

中图分类号：TN92

文献标志码：A

文章编号：1002-0802(2016)01-0062-06

基金项目：国家自然科学基金青年项目(No.61301160)Foundation Item:National Natural Science Foundation of China(No.61301160)

*收稿日期：2015-08-20；修回日期：2015-11-29Received date:2015-08-20；Revised date：2015-11-29

doi:10.3969/j.issn.1002-0802.2016.01.013