APSK与极化码级联系统星座优化设计方案*

成风毅，刘爱军，张青双，张应宪

(解放军理工大学 通信工程学院，江苏 南京 210007)



APSK与极化码级联系统星座优化设计方案*

成风毅，刘爱军，张青双，张应宪

(解放军理工大学 通信工程学院，江苏 南京 210007)

摘要：针对基于极化码同幅相键控调制(APSK)级联系统，首先简述了APSK调制方案和极化(Polar)码构造过程，阐述了APSK星座图上内外圆半径比R与信道容量I(W)之间的关系。在此基础上，分析了级联后系统的信道二次极化过程，针对极化码译码流程，基于密度进化(DE)算法优化了系统星座图设计。理论分析和仿真结果表明，该算法能够兼顾系统性能和复杂度，可为基于Polar码的高阶调制系统星座优化设计问题提供技术参考。

关键词：APSK；星座设计；极化码；密度进化；信道

0引言

在实际卫星通信系统中，为提高APSK系统的性能，通常会同时采用具有逼近香浓极限特性的LDPC码和Turbo码：这种方案能够在一定阶段解决通信的可靠性问题，然而在此两种编码方式同APSK的级联系统中，往往是将编码和调制分离设计，并没有将编码和调制看成一个整体系统，本文基于信道变换的角度，将调制和编码看为一个整体进行联合设计，寻求对APSK星座图进行优化设计。

作为目前唯一证明可以获得香农极限的编码方式，极化码具有对数编译码复杂度，并且可灵活的实现码字重构。基于Polar码的APSK通信系统与LDPC/Turbo码系统相比具有较低的检测复杂度和潜在的性能优势，这也是本文的主要研究的出发点。

提高基于Polar码的APSK系统性能的关键在于如何设计APSK星座图以保证所选择的极化后子信道容量和最大[1]。针对该问题，首先分析了信道极化过程对星座图设计的影响。在此基础上，采用DE方案，分析了级联系统的可靠性指标与APSK星座图内外半径比的关系，进而设计出APSK最佳星座图，最后仿真结果验证了该算法的有效性。本文所提方法可为基于Polar码的高阶调制系统星座优化设计问题提供技术参考。

1基本原理

1.1APSK调制

M-APSK的星座图通常由分布在若干个同心圆上的点构成[2]。对于16阶APSK调制，一般可以用i+jAPSK形式来表示，其中i表示星座图内圆上的点数，j表示为星座图外圆上的点数，一般j>i。设为M-APSK信号星座点集合，可给出其表达式为：

(1)

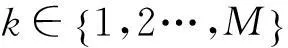
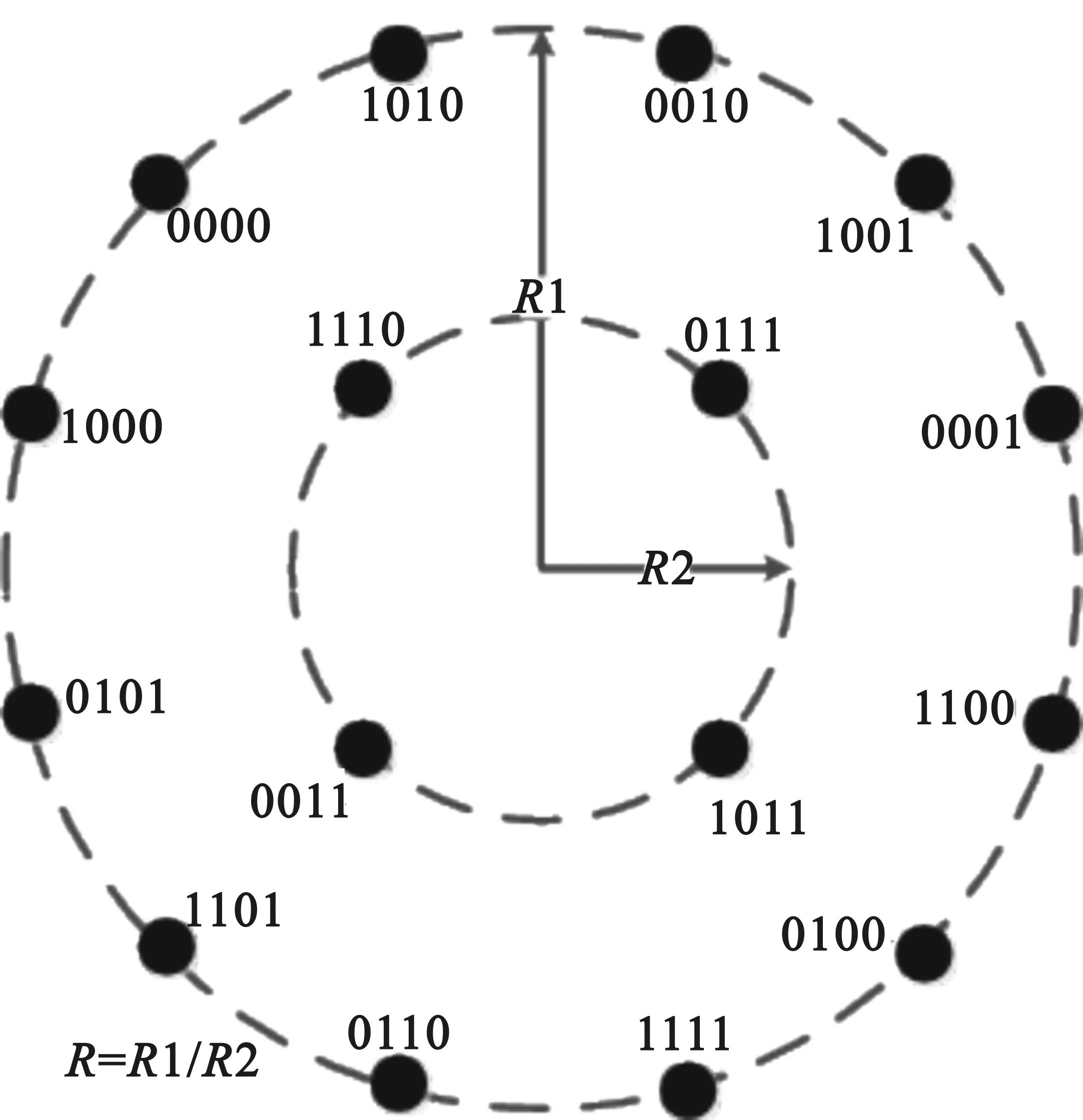
图1　4+12APSK星座图

在调制的时候应当满足功率归一化，即：

(2)

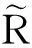
1.2极化码的构造

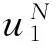
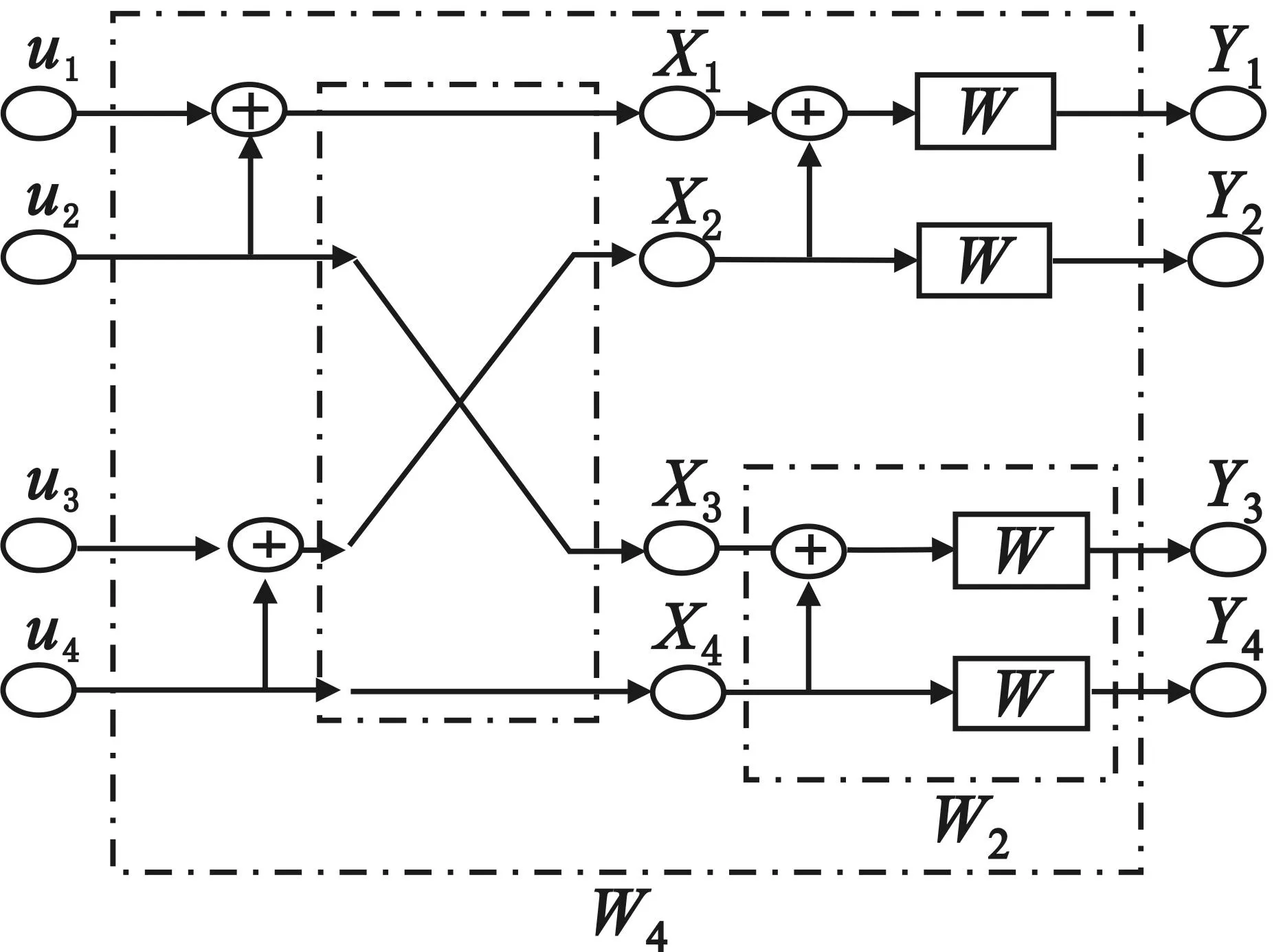
图2　极化码W4、W2、W之间关系

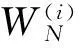
2基于Polar码的APSK级联系统

2.1系统模型

图3为系统级联模型，K比特信息流分配给4组码长为N的极化编码器，其中设计码率控制，使得四组极化码的总码率得以保证为所需码率。信息流经过极化编码GN之后，输出4个码长为N的比特序列，将这4个比特序列分别按序取1个比特，即可组成一个 16进制的符号信息。

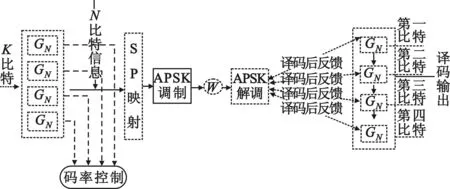
图3　Polar-APSK级联系统简单模型

由于解调方案是逐位解调，即上一比特解调结果作为解调下一比特的条件，故采用分集(SP，Set Partition)映射，即将信号星座点分组，原则是使每次分组该组内的点具有尽可能大的欧式距离。这种映射比起格雷映射优势是第一位比特解调时欧式距离是最大的，保证了往后逐位解调的可靠性。

如前所述方案，进行逐位解调，解调出全部符号信息第一比特的软信息序列后，送入对应的译码模块，译码后将译码结果反馈给解调器进行下一位解调译码的条件，直至所有比特译出，最后根据极化码信息位检索出传输信息K比特。

2.2系统信道转换

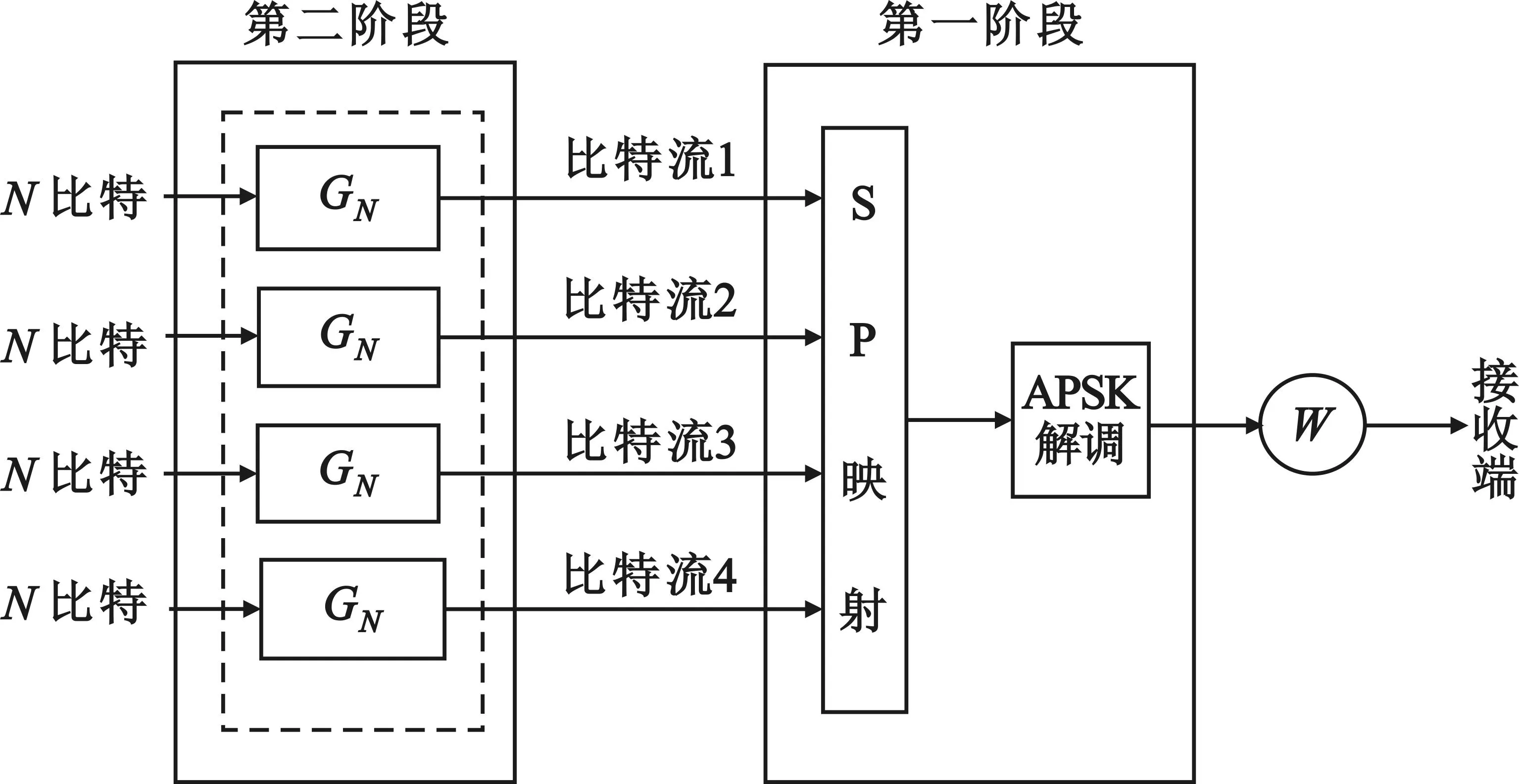
图4　Polar-APSK级联发送流程

2.3信道容量及转移概率

在二进制对称信道中，我们常用信道转移概律来评价信道可靠性，信道对称容量往往可由信道转移概率求得，即：

(3)

这意味着，只需知道子信道转移概率，即可评价信道性能。下面我们就2.2节给出的两个阶段信道转移概率分别进行分析。

对于二进制无记忆信道，基于SC译码条件下子信道的转移概率为：

(4)

(5)

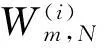
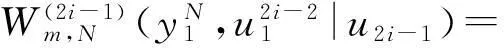
(6)

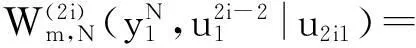
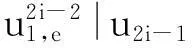
(7)

由此，我们将整个信道变化中的转移概率密度全部求出。

由上可知，信道容量可由信道转移概率求出，由式(3)、(5)、(6)、(7)，并结合对称信道容量同转移概率的关系，有下式：

(8)

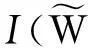
(9)

至此可知，只需知道子信道的转移概率，即可求出系统对称容量，且结合式(9)可知经过星座映射后，整个系统的总对称容量I(W)并没有发生变化。意味着极化充分后，MPCM系统没有必要进行星座设计。但在实际工程中，由于码长有限导致的极化不充分，使得子信道信道容量不能完全等于0或1，故信息位的误码率必然不等于0，这意味着码率在小于I(W)时也会有误码。

也就是说，在信息位信道容量不足够接近1时，即低信噪比环境或高码率情况下，对星座图设计是有必要的。

3基于密度进化算法的星座图设计

3.1系统容量与半径比关系

由式(5)可知，不同的星座映射，信道转移概率并不相同，而信道转移概率同信道对称容量关系如式(8)、(9)所示。自然地想到半径比R同子信道对称容量I(W)之间存在某种关系，不妨定义为：

Im(W)=fm(R)

(10)

Itotal=g(Il,I2,I3,I4)

(11)

m取值为1,2…4 ,Itotal为所选取的信息位信道容量的总和。由式(10)、(11)可知，系统总的信道容量和星座图半径R之间关系有：

Itotal=g(f1(R),f2(R),f3(R),f4(R))

(12)

(13)

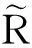
然而，由于往往没有办法求得式(13)的闭合解，同时由误码率同信道容量成反比关系，故可以文献[6-7]中的DE算法构造极化码，在不同半径比条件下，由子信道似然比的概率密度，求出误码率，找到使误码率最小的半径比。

3.2基于密度进化算法的最优半径比求解

密度进化算法的核心思想就是通过计算极化后每个子信道软信息的概率密度，然后统计其误比特率，进而选择其中误比特性能较好的子信道作为传输信息的信道，这些子信道的平均误比特率反应了在给定半径下系统性能的好坏。

图4为级联系统利用DE算法构造极化码的流程图。系统同样存在两个信道变化阶段，第一阶段是经过高斯信道到达Y点，此时有：

y=s+n

(14)

y是接收序列，s是发送序列，n是方差为σ2的白噪声。

整个密度进化包括两个阶段。第一阶段为由信道的高阶符号统计4个比特软信息的概率密度，其中每个比特的软信息可以通过下面公式得到：

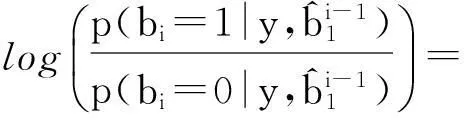
(15)

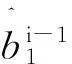
获得每个比特的软信息后，通过统计方式即可得到相应的概率密度。在统计每个比特软信息的概率密度时需要前级的比特的硬判决值作为先验信息，在码子构造阶段此硬判决值可假设全部正确判决。

第二个阶段即为信道极化过程。如图4所示，将第一阶段获得的概率密度信息分别进行信道极化，即可获得所有子信道的概率密度。图5给出了极化码的基本处理单元，在已知输入信息的概率密度时，输出概率密度的计算公式为：

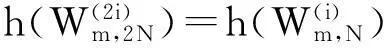
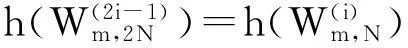
g3=g1⊗g2,g4=g1*g2

式(16)中的⊗和*运算为文献[8]中定义的卷积运算。

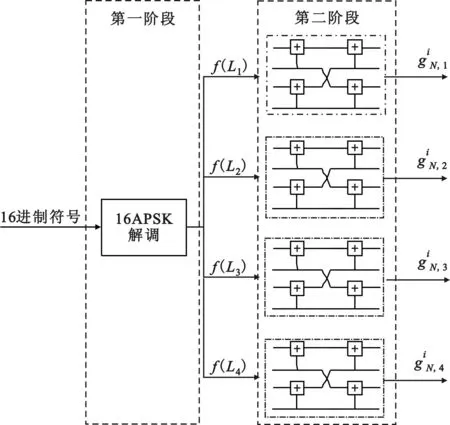
图4　polar-APSK级联极化码构造流程

图5　极化码基本处理单元

求得所有子信道概率密度函数后，即可求得每个子信道误码率：

(17)

式中，h(x)为译码输出子信道似然比信息的概率密度函数(probability density function，PDF)，在得到极化后每个子信道的误比特率以后，挑选其中K个最好的信道作为信息信道，其序号集合为A，则整个系统的平均误比特性能可近似为：

(18)

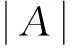
4仿真结果与分析

主要针对Polar—APSK级联系统的译码输出子信道概率密度演进结果，以及ratio-Pe之间的关系进行仿真分析。下列仿真条件均假设信道为AWGN信道，Polar码码长设为N=27=128。由于挑选子信道为分析误码率的首要过程，故我们首先分析了译码器输出端各子信道PDF的演进结果。

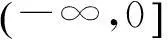
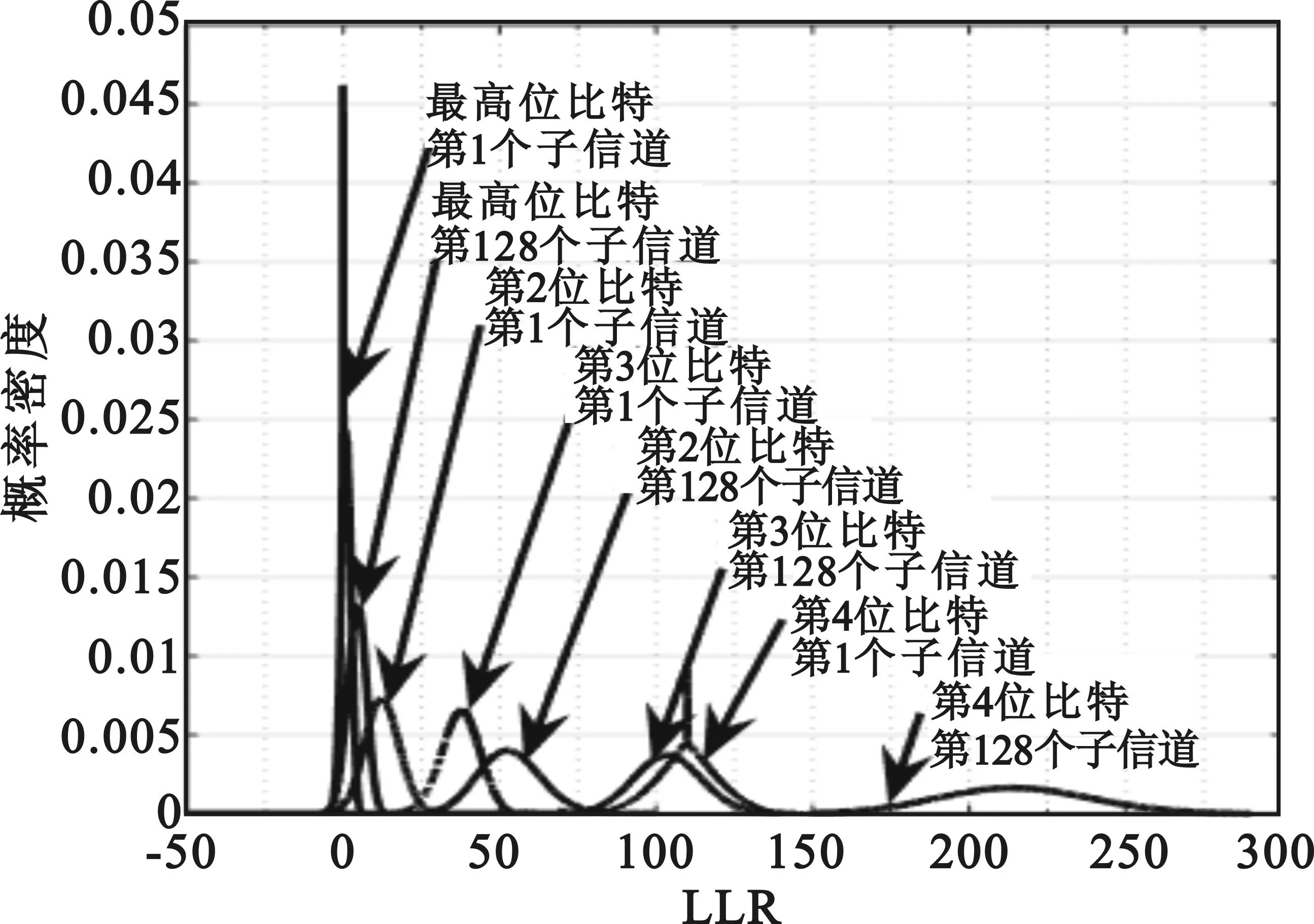
图6　Polar-APSK级联系统译码输出子信道密度演进

图7描述了在Eb/N0=4.5 dB，Polar码码长为128，子信道传输100 000帧时，编码信息位误码率总和根据不同码长归一化后同R之间的关系。可以看出在高码率情况下，MPCM系统由于信息位的信道容量有较大一部分小于1，故R对编码影响更为严重，此时选择了大部分性能较差的子信道作为信息位，故误码率较高。随着码率的变小，所选取得子信道信道容量均趋近于1，故系统性能逐渐变好，且此时不同星座内外圆半径对于信道性能影响不大。

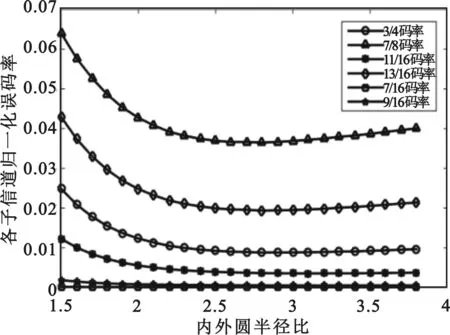
图7　内外圆半径比同误码率之间的关系曲线

表1给出了信噪比在4.5 dB时，不同码率情况下，APSK最佳工作半径的取值及误码率大小。

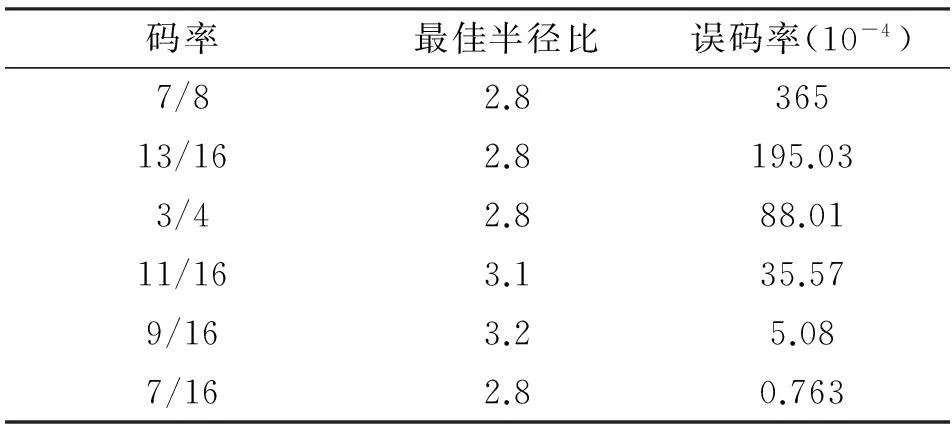
表1　基于APSK—Polar系统的各码率最佳半径比及误码率

由图8所示，在级联系统中，按本文设计方案给出的最优半径与之前文献中描述的最优半径2.7时性能有所提升。在4.5 dB左右可见，此时误码率比起表1给出结果要差，原因是在表1的逐位解调中，由于仅需比较子信道性能，故均假设前一位译码全部正确。而在信噪比较大(SNR>7 dB)，或者时码率较小时，由于逐位解调时第一位解调已经性能很好，星座图的设计对性能影响并不大，故性能曲线趋于接近。这与2.3节给出的结论一致。

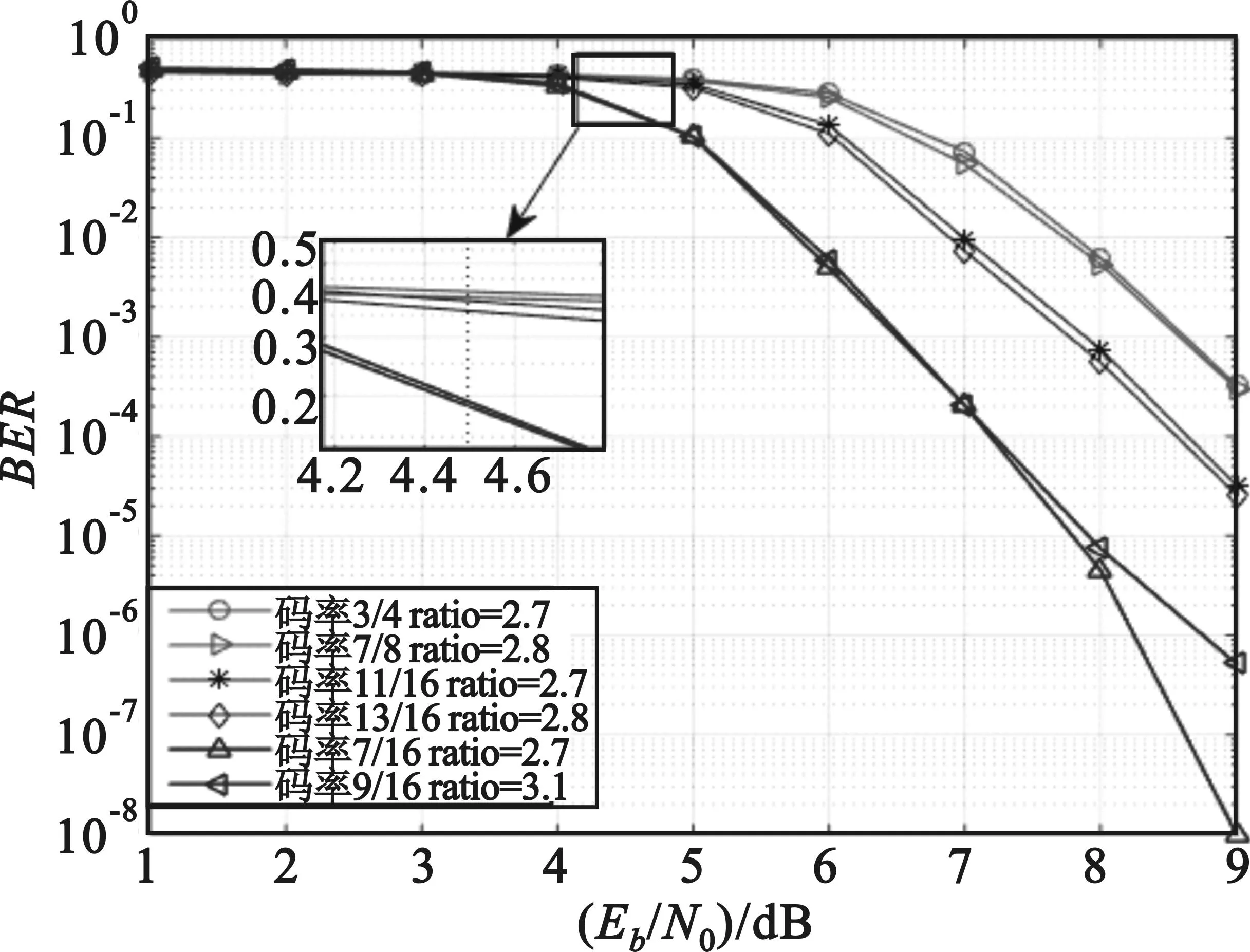
图8　半径比同误比特率之间关系

5结语

论文针对Polar-APSK系统，基于系统最小误码率准则，给出了级联系统中APSK星座图的一种优化设计方案。故本文采用了DE算法，该算法最大优势在于可以适用于包含BAWGN信道在内的大部分信道，且结果较为精密。此方案不仅适用于APSK同Polar级联的方式，在其他调制编码联合极化领域亦适用，可将调制过程看作信道的变化过程糅合到极化编码中去，且不存在Turbo码级联时出现的误码平层问题。也应当注意DE算法同样存在卷积计算量大，在级数较高情况下卷积长度过长等问题。

参考文献：

[1]Arikan E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels [J]. IEEE Transactions on Information Theory, 2009, vol. 55(7): 3051-3073.

[2]Thomas C M, Weidner M Y and Durrani S H. Digital Amplitude Phase Keying with M-ary Alphabets [J].IEEE Transaction Communication, 1974, vol. 22(2):168-180.

[3]Einarsson G. SignalDesign for the Amplitude-Limited Gaussian Channel by Error Bound Optimization [J].IEEE Transaction Communication, 1979, vol. 27(1):152-158.

[4]Arikan E. Channel Combining and Splitting for Cutoff Rate Improvement [J]. IEEE Transaction on Information Theory, 2006, vol.52 (2):628-639.

[5]李斌,王学东,王继伟.极化码原理及应用[J].通信技术,2012,45(10):21-23.

LI Bin, WANG Xue-dong and WANG Ji-wei. Theory and Application of Polar Code[J]. Communications Technology, 2012, vol. 45(10):21-23.

[6]Mori R, Tanaka T. Performance and Construction of Polar Codes on Symmetric Binary-Input Memoryless Channels [C]// Information Theory Conference (ISIT). Seoul:IEEE,2009:1496-1500.

[7]Mori R, Tanaka T. Performance of Polar Codes with the Construction using Density Evolution[J]. IEEE Communications Letters, 2009, vol.13(7):519-521.

[8]Richardson T, Urbanke R. ModernCoding Theory [M]. First Edition, Britain: Cambridge University Press, 2008:pp.434.

成风毅(1988—)，男，硕士研究生，助教，主要方向为卫星通信；

刘爱军(1970—)，男，教授，主要方向为卫星通信；

张青双(1989—)，男，博士研究生，主要方向为卫星通信；

张应宪(1987—)，男，博士，主要方向为卫星通信。

术语百科Technical Terms

低噪声放大器(LNA)

噪声系数很低的放大器。一般用作各类无线电接收机的高频或中频前置放大器，以及高灵敏度电子探测设备的放大电路。在放大微弱信号的场合，放大器自身的噪声对信号的干扰可能很严重，因此希望减小这种噪声，以提高输出的信噪比。由放大器所引起的信噪比恶化程度通常用噪声系数F来表示。理想放大器的噪声系数 F=1(0分贝)，其物理意义是输出信噪比等于输入信噪比。现代的低噪声放大器大多采用晶体管、场效应晶体管;微波低噪声放大器则采用变容二极管参量放大器，常温 参放的噪声 温度Te可低于几十度(绝对温度)，致冷参量放大器可达20K以下，砷化镓场效应晶体管低噪声微波放大器的应用已日益广泛，其噪声系数可低于 2 分贝。放大器的噪声系数还与晶体管的工作状态以及信源内阻有关。为了兼顾低噪声和高增益的要求，常采用共发射极一共基极基联的低噪声放大电路。

Constellation Optimization Scheme in APSK and Polar-Code Cascade System

CHENG Feng-yi，LIU Ai-jun，ZHANG Qing-shuang，ZHANG Ying-xian

(College of Communication Engineering, PLA University of Science and Technology, Nanjing Jiangsu 210007, China)

Abstract：For making an analysis on Polar code based APSK communication systems, this article begins with a brief introduction of APSK signal model and polar-code construction, then describes the relations of between inside-and outside- on APSK constellation radius ratio(R) and channel capacity, and then discusses subchannel performance by using transition probabilities. And after elaborating the secondary process of channel polarization in MPCM system, a density evolution algorithm is proposed to compute the system reliability, which is expected to help find out the optimal APSK constellation shaping design. Theoretical analysis and simulation indicate that this algorithm could give consideration to both system performance and complexity, and is thus superior to the existing part of the literature. The proposed method in this paper could provide a technical reference for optimal constellation design of high-order modulation system based on polar code.

Key words：APSK; constellation design; polar code; density evolution ; channel

作者简介：

中图分类号：TN911.3

文献标志码：A

文章编号：1002-0802(2016)01-0012-06

基金项目：国家自然科学基金资助项目(No.61501508)Foundation Item:National Natural Science Foundation of China (No.61501508)

*收稿日期：2015-08-16；修回日期：2015-11-28Received date:2015-08-16；Revised date：2015-11-28

doi:10.3969/j.issn.1002-0802.2016.01.003