单载波短波数字信号MMSE均衡算法研究*

佟长凯，应文威，李成军

(中国人民解放军91635部队，北京 102200)



单载波短波数字信号MMSE均衡算法研究*

佟长凯，应文威，李成军

(中国人民解放军91635部队，北京 102200)

摘要：由于受到多径效应的影响，短波数字信号受到严重的码间串扰影响，针对短波数字通信的特点设计了基于训练周期的LC app MMSE均衡算法，算法设计过程中又对信道冲激响应估计、训练序列的处理等问题提出了解决方法。基于训练周期的LC app MMSE算法充分利用训练序列估计信道特征，降低了由于信道时变对均衡算法的影响，在运算复杂度及性能上实现了良好权衡。最后对提出的方案及算法进行了性能分析及仿真验证，仿真结果表明设计的算法性能良好具有一定的应用价值。

关键词：码间串扰；Turbo均衡； MMSE算法

0引言

短波通信具有通信距离远、开通迅速、抗毁性强、网络重构便捷、机动灵活等特点，在军事及应急通信中得到广泛应用[1]，但由于其依靠不稳定的大气电离层反射传播电磁波，因此短波数字通信质量受到多径效应、时变色散、衰落严重、干扰复杂等严重影响。短波通信系统应对这些不利因素影响的重要手段是通过均衡技术矫正信道畸变。传统均衡技术在处理短波信道时往往性能有限，而Turbo均衡技术通过引入译码增益可以取得良好均衡性能。

经典的Turbo均衡算法是由Douillard等人提出的最大后验概率(Maximun A Posteriori，MAP)算法[2]，但这种算法运算量同信道冲激响应长度成指数关系，不适于短波信道这种存在严重码间串扰的无线信道。另一种算法是Michael Tüchler 等人提出了基于先验信息的MMSE(Minimum Mean Squared Error)均衡算法[2-3]，这种算法以较小的性能损失将运算复杂度降为均衡器长度的平方关系。后来Michael Tüchler等人又提出LC app MMSE(Low-Complexity approximate MMSE)均衡算法[3-7]将运算复杂度进一步降为均衡器长度的线性关系。

但MMSE算法和LC app MMSE算法都需信道已知及恒定条件下进行，这显然不能直接应用于短波信道，必须对其进行预处理及改进以使其适用短波这种未知时变信道。本文主要根据短波信道特点及短波数字通信信号特点对MMSE算法及LC app MMSE算法展开研究，包括信道冲激响应估计、训练序列概率信息设置、及算法改进等问题，使其适用于短波数字通信。

1MMSE均衡算法

对于短波信道来讲最常用的信道模型为Watterson模型[1]。因此本文在进行算法推导过程中也采用这种模型对短波信道进行仿真。根据Watterson模型其信道冲激响应可表示为：

(1)

yn=H·xn+wn

(2)

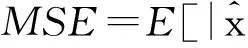
(3)

由于信号通过ISI信道，所以上式可写为:

(4)

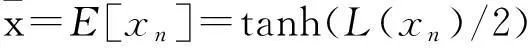
s=H[01×(N2+M-1)101×N1]T

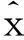
(5)

均衡器输出为：

(6)

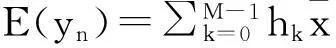
cn=(σ2I+HVnHH+(1-vn)ssH)-1s

(7)

因此最后均衡器估计值为:

(8)

其中 ：

(9)

(10)

因此均衡器输出软信息为:

(11)

上式中外部信息的计算采用的是估计值而不是观测值，即在经过均衡后对均衡后数据进行处理来得到外部信息。均衡器输出的信息序列的对数似然比经过解交织后即可作为译码器的先验信息，而译码器输入的信息序列对数似然比经过交织后输入的均衡器中用于计算均衡器输入数据的E[xn]、Cov{xn,xn}，见图1。式(5)中的求逆运算可以根据矩阵求逆引理进行迭代计算，以降低算法运算量，采用此法后算法复杂度为O(N2)。

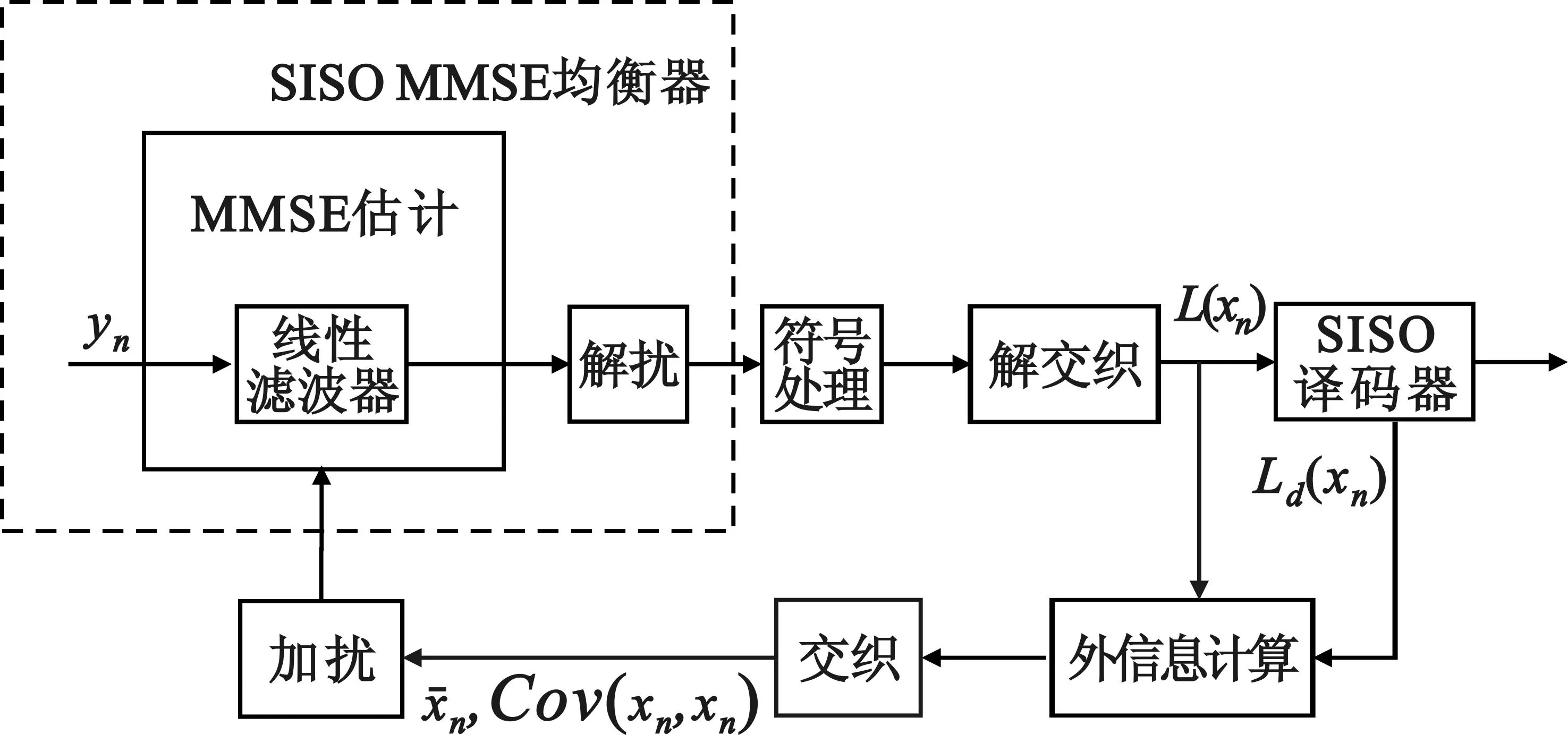
图1　MMSE衡器算法流程

2短波MMSE-Turbo均衡器的构造

短波信号常见的帧结构如图2所示，导频头用于信号监测及载波估计，先导序列位于导频头之后用于检测突发数据的开始位置、测量并校正由于多普勒频偏和接收机、发射机频偏造成的频率偏移、判断传输模式、位同步、信道估计或训练均衡器。由于短波信道是一个时变信道，数据帧中每隔数个数据为就会穿插一定位数的训练序列用于跟踪信道变化。为了提高信息传递的可靠性，短波数字通信普遍采用卷积码作为其前向纠错码。

图2常见短波信号帧结构

根据图1中MMSE算法流程及短波信号的帧结构，在进行均衡运算前，还需几步准备工作：

(1)信道冲激响应估价及信噪比估计；

(2)训练序列的符号软信息设置。

1)信道冲激响应估计

在算法的推导过程中，我们发现整个算法都是基于已知信道进行的，而在实际应用中，信道的冲激响应是未知的，为此在进行均衡运算前必须对信道的冲激响应进行估计。最常用的两种信道冲激响应算法为LMS算法和RLS算法。不同于常规的的均衡算法依据某种准则求出滤波器系数wk

(12)

(13)

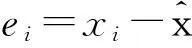
2)训练序列的符号软信息设置

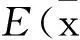
3基于训练周期的LC app MMSE算法

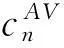
(14)

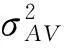
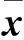
于是滤波器系数向量可写为：

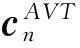
(15)

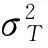
算法复杂度：MMSE均衡算法的运算量主要集中在对接收信号的求逆运算上，当求逆运算采用矩阵求逆引理时其复杂度为O(N2)，而基于训练周期的LC app MMSE均衡算法每个周期只需进行一次求逆运算因此其复杂度约为为MMSE算法的1/K，K为一个训练周期信息符号的长度，这种运算量对于Turbo均衡来说是可以接受的。

4性能分析及仿真

仿真分析采用典型的Proakis’B信道[8]，其冲激响应为：

h(n)=0.407δ(n+1)+0.815δ(n)+0.407δ(n-1)

(16)

仿真信号按照常见的单载波数据链信号构造，前导序列长度设为500个符号，每120个数据符号插入30个符号的训练序列，交织长度2 048，BPSK调制。对均衡算法性能分析最常用的方法就是外部信息转移图(Extrinsic Information Transfer, EXIT)，通过观察输入输出数据的互信息量比较性能。

图3为Eb/N0=5时，在Proakis’B信道条件下两种算法的EXIT图，从图中可以看出MMSE均衡算法的性能要好于基于周期的LC app MMSE均衡算法，两种算法在输入信息互信息量较低时两种算法信息相似，而随着互信息量升高算法性能差异增加，但当输入互信息量接近1比特时性能差距减少，最终达到约0.85比特，从图中可看出两种算法性能差距并不大，但其运算量基于训练周期的LC app MMSE算法约为MMSE算法的1/120。

图4为采用基于训练周期的LC app MMSE均衡算法及采用MMSE均衡算法的Turbo均衡器误码率图，Turbo均衡器采用的译码算法为LOG-MAP算法，信道估计算法为RLS算法。均衡器迭代次数设置为5。作为对比同时采用DFE均衡，DFE前馈滤波器阶数及后馈滤波器阶数均为15，训练模式采用遗忘因子为0.999 95的RLS算法，均衡模式采用步进0.000 01的LMS算法，均衡后采用软输入维特比算法进行译码。从图中可看出，采用两种不同算法的Turbo均衡器的性能要远远优于传统的DFE，Turbo均衡器当Eb/N0=7即可实现近似无差错的传输了，而此时DFE的误码率还高达10-2以上。而采用MMSE算法和LC app MMSE算法的Turbo均衡器性能接近，在信噪比较低时MMSE算法性能较LC app MMSE高出约0.4Db，而当Eb/N0≥5两者性能近似，而此时LC app MMSE算法的复杂度约只为MMSE算法的1/120。由此可见LC app MMSE已较小的性能损失为代价大大降低了运算复杂度。

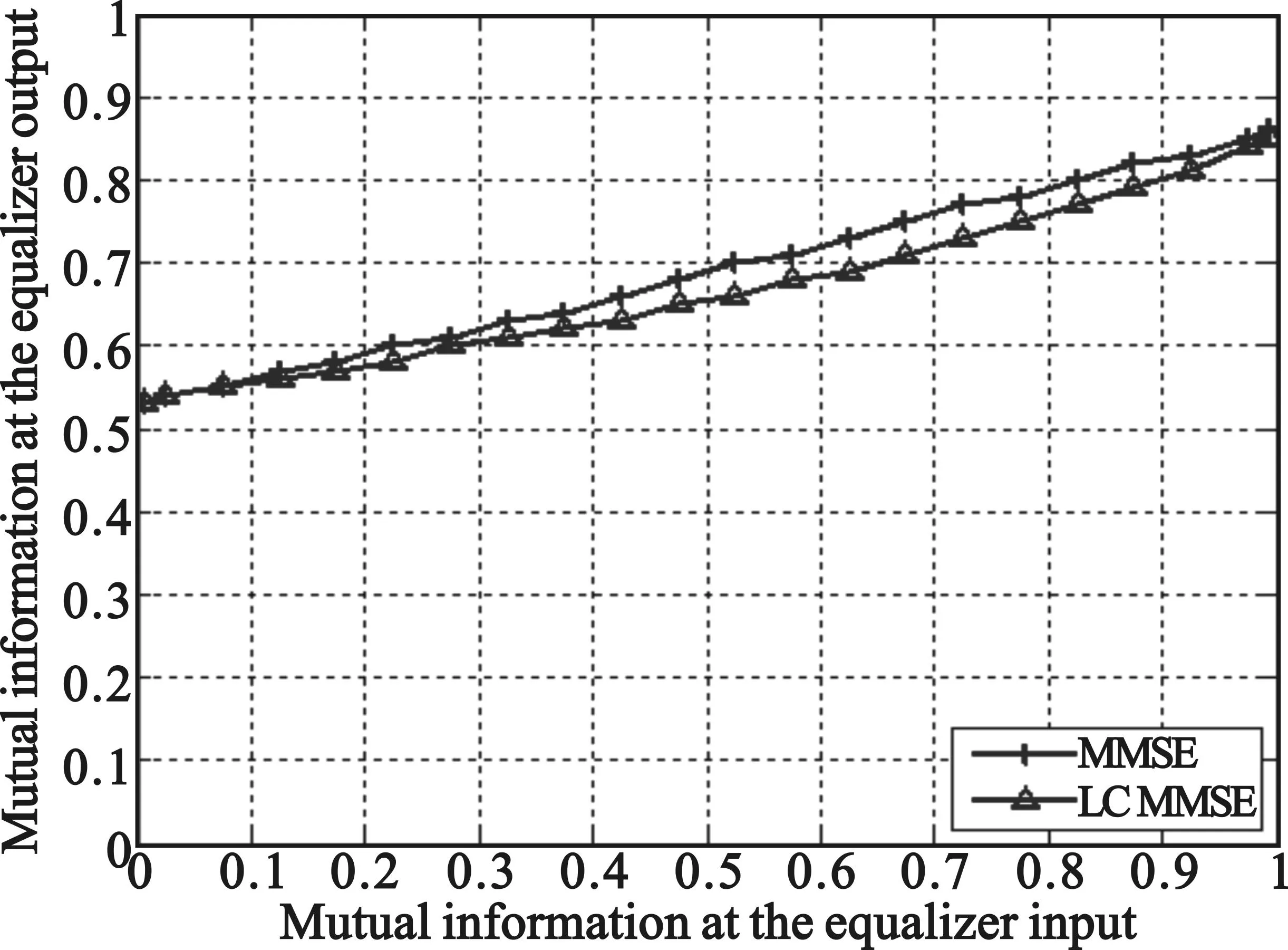
图3　MMSE算法及基于训练周期的

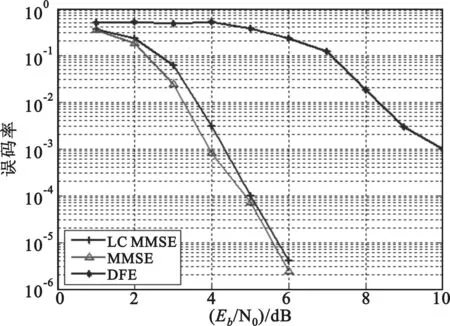
图4　三种均衡算法误码率

4结语

信道均衡技术是通信系统对抗恶劣信道的重要手段，本文针对单载波数字通信特点对Turbo均衡算法的MMSE均衡算法及LC app MMSE均衡算法展开研究，对其性能及复杂度进行了分析并根据短波数字通信特点改进了LC app MMSE均衡算法使其更加适应短波时变信道特性，仿真结果可以看出其性能要较传统均衡算法有大幅提升。随着短波数字通信系统的迅速发展，短波信道的均衡技术也将得到广泛应用，本文设计的均衡算法充分考虑了短波信道特点，权衡运算复杂度及均衡性能，对今后短波信道Turbo均衡器设计具有一定的实际应用价值。

参考文献：

[1]王金龙．短波数字通信研究与实践[M].北京：科学出版社，2013：15-20．

WANG Jin-long. Research And Practice of HF Digital Communication[M]. Science Press. 2013:15-20.

[2]Michael Tüchler, Ralf Koetter, and Andrew C Singer. Turbo Equalization: Principles and New Results[J]. IEEE Transactions on Communctions. 2002,50(5):754-767.

[3]Michael Tüchler, Andrew C. Singer and Ralf Koetter. Minimum Mean Squared Error Equalization Using A Priori Information[J]. IEEE. Transactions on Signal Processing. 2002. 50(3). 673-683.

[4]张桂祥， 罗秋霞， 胡飞.多径信道Turbo 均衡技术性能分析[J].通信技术,2007,40(12):29-31.

ZHANG Gui-xiang, LUO Qiu-xia, HU Fei. Performance Analysis of Turbo Equalization Technology under Multipath Channels[J]. Communications Technology, 2007. 40(12).29-31.

[5]Bouchra Benammar, Nathalie Thomas, Charly Poulliat. On Linear MMSE based Turbo-Equalization Of Nonelinear Volterra Channels[C]. ICASSP. IEEE. 2013:4703-4707.

[6]Tchler M, Singer A C. Turbo Equalizer: An Overview[J]. IEEE Trans. Inf. Theroy. 2011,57(2):920-952.

[7]Valeria Arlunno, Antonio Caballero, Robert Borkowski, et al. Turbo Equalization for Digital Coherent Receivers[J]. Journal of Lightwave Technology. IEEE. 2014. 32(2):275-279.

[8]John G, Proakis .Digital Communications (Fifth Edition)[M]. Publishing House of Electronics Industry.2009:830-831.689-695.

佟长凯(1986—)，男，硕士研究生，主要研究方向为数字信号处理；

应文威(1987—)，男，博士，主要研究方向为数字信号处理；

李成军(1976—)，男，博士，主要研究方向为通信信号处理。

HF Signal Carrier Digital Signal MMSE Algorithm

TONG Chang-kai, YING Wen-wei, LI Cheng-jun

(Unit 91635 of PLA, Beijing 102200, China)

Abstract：Due to the influence of multipath effects, HF digital signal is affected by severe ISI(Inter-Symbol Interference). Aiming at the characteristics of HF digital communication, LC app MMSE algorithm based on training period is designed.And solutions for some problems, including estimation of channel impulse response and processing of training sequences are proposed in the process of algorithm design. By taking full advantage for the characteristics of training sequences in channel estimation, the newly-design algorithm could lower the influence on load-balancing algorithm brought by time-varying channel and achieve a fairly good trade-off of between computational complexity and performance. Finally, performance analysis and simulation verification on the proposed scheme,indicate that the newly-designed algorithm is of fairly good performance and certain application value.

Key words：ISI; Turbo equalization; MMSE algorithm

作者简介：

中图分类号：TN911

文献标志码：A

文章编号：1002-0802(2016)01-0052-04

*收稿日期：2015-08-11；修回日期：2015-11-28Received date:2015-08-11；Revised date：2015-11-28

doi:10.3969/j.issn.1002-0802.2016.01.011