一种高动态环境下频偏粗估改进算法研究*

王雅慧，叶　展，郭道省，杨晗竹

(解放军理工大学 通信工程学院,江苏 南京 210007)



一种高动态环境下频偏粗估改进算法研究*

王雅慧，叶展，郭道省，杨晗竹

(解放军理工大学 通信工程学院,江苏 南京 210007)

摘要：针对高动态环境下信号传输存在大频偏以及频率变化率的问题，在分段累加FFT算法的基础上提出了新的算法。该算法首先对接收数据进行分组，然后分别对每组数据的频偏及其变化率采用传统分段累加FFT算法进行粗估计，再将得到的粗估值补偿到对应的数据段中，在此基础上进行下一步的细同步估计。仿真结果表明，新算法的估计精度提高了近50%，对于高动态环境下的频偏估计具有一定的适用性。

关键词：高动态；粗估计； FFT

0引言

卫星移动通信具有高动态低信噪比的特点，这导致卫星通信信号存在大多普勒频偏以及频率高阶变化率，给信号的同步和解调带来困难。卫星移动通信中，由于卫星和通信终端之间的快速相对运动，带来较大的多普勒频偏；同时，受制于卫星和终端能力，移动卫星通信中符号速率往往较低。两者综合的结果导致卫星移动通信中，多普勒频偏往往可达符号速率的几十倍甚至上百倍，同时存在严重的频率变化率[1]。

信号的同步可以分为载波同步和位定时同步。一般的接收机中，通常首先完成对接收信号的位定时同步，然后在此基础上进一步完成载波同步(包括频率同步和相位同步)。但这样做的前提是接收信号仅存较小的频偏(一般要求频偏限制在10%的符号速率以内)，如果频偏进一步增大，会导致位定时同步性能严重恶化，甚至无法完成位定时同步。而本文所研究的高动态场景，频偏远远超过了位定时同步所要求的10%符号速率范围，无法直接完成信号的位定时同步[2-3]。

针对高动态环境的特点，可将信号的载波同步分为两部分：粗同步和精同步。

粗同步又被称为参数捕获，先对高动态环境下接收信号的频偏进行初步估计，并用混频器将频偏抵消或者将参数估计值送入跟踪器以帮助跟踪器快速进入锁定状态，后者则在前者基础上进入跟踪器进行精度更高的估计(包括载波频率、相位以及位定时估计)。文献[4]提出一种基于LS准则的载波参数估计方法，该方法通过搜索周期图峰值的方法得到频偏估计值；若用于载波估计的数据长度为L，对L个采样数据进行傅立叶变换，得到信号的频谱图峰值而推论出的位置即为载波频偏的粗估值。为了后面精同步的需要，可以通过在L个数据后面补L个0，再进行傅立叶变换，这样的运算并没有改变周期图的形状，只是提高了频谱分辨率[5]。但是这样提高FFT运算长度会造成运算量和存储量的大大增加。为了满足估计性能要求又不增加FFT长度，文献[6]提出利用分段FFT累加的方法进行频偏的粗估计。其思路是将整个观测区间长度分为若干等长观测区间，进行分段FFT后累加再寻找频率估计值。但是文献[6]仅对低信噪比条件下的大频偏信号的频偏粗估进行了讨论和仿真，不适合用在高动态环境中。

本文从卫星移动通信在高动态环境下的特点出发，对分段累加FFT算法进行改进，不仅提高了粗同步过程的频偏估计精度，还增加了对信号频偏变化率的估计工作，为后续精同步工作的进行创造了更好的条件。

1信号模型

1.1高动态环境下的信号模型

根据文献[7-8]可知，高动态环境下，接收机接收到的信号复包络可以表示为：

(1)

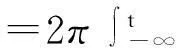
由于物体运动速度轨迹与多普勒频率轨迹之间满足下式：

(2)

式中，vd(t)为物体的相对运动速度，fc为信号载波频率。fd(t)在t0附近的泰勒级数展开式为：

(3)

在t0=0附近，观测区间的载波相位为：

(4)

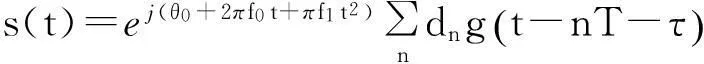
(5)

1.2传统算法信号模型

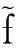
(6)

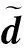
2传统分段FFT算法

根据文献[6]的介绍，对式(6)用泰勒级数ex≈1+x+x2/2 进行近似计算，可以得到：

(7)

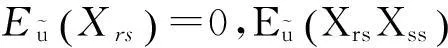
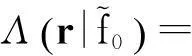
(8)

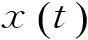
(9)

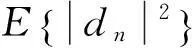
(10)

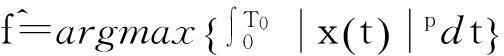
在此基础上继续通过傅里叶逆变换进行推导，假设X(f)为观察区间0～T0内x(t)所对应的傅里叶变换，有：

(11)

此时载波频率的似然估计值为：

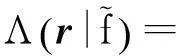
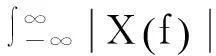
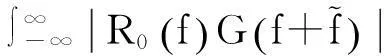
(12)

(13)

(14)

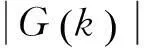
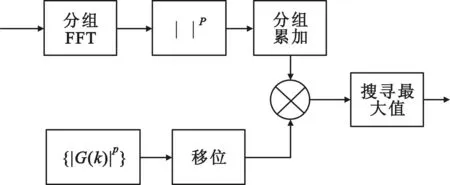
图1　分段FFT累加法估计大频偏实现框

3改进分段累加FFT算法

根据高动态环境下信号模型的分析可知，接收端的接收信号在不同时刻的频偏是不同的，与传统分段累加FFT算法中固定大频偏的环境相差很多。

如图2所示是高动态环境的频偏变化曲线图。此时接收信号存在频偏一阶变化率。由于信号的频偏每时刻都在变化，当存在多阶变化率时，信号频偏变化会更快。基于这点考虑，文中提出了一种改进的分段累加前向估计算法，该算法不仅可以提高粗估阶段的估计精度还可以估计出频偏变化率。改进的基本思路如下：由于信号频偏及频偏粗估计过程对估计精度要求不高(仅要求信号在粗估计补偿后达到符号速率的10%以内)因此首先将信号频偏及频偏变化率看作一个整体进行估计。此时接收信号复包络可以表示成：

(15)

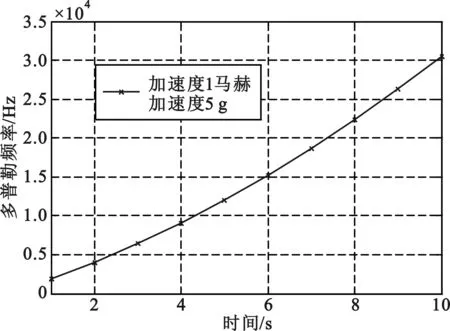
图2　多普勒频率偏移变化曲线

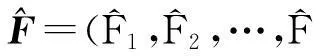
(16)

通过分组至少可以得到两个方程组，因此可以通过差分运算得出频偏一阶变化率的估计值：

(17)

当信号的频偏存在多阶变化率时，可以通过增加分组数根据式(4)进一步计算，来获得信号的多阶频偏变化率。

具体流方框图如图3所示。

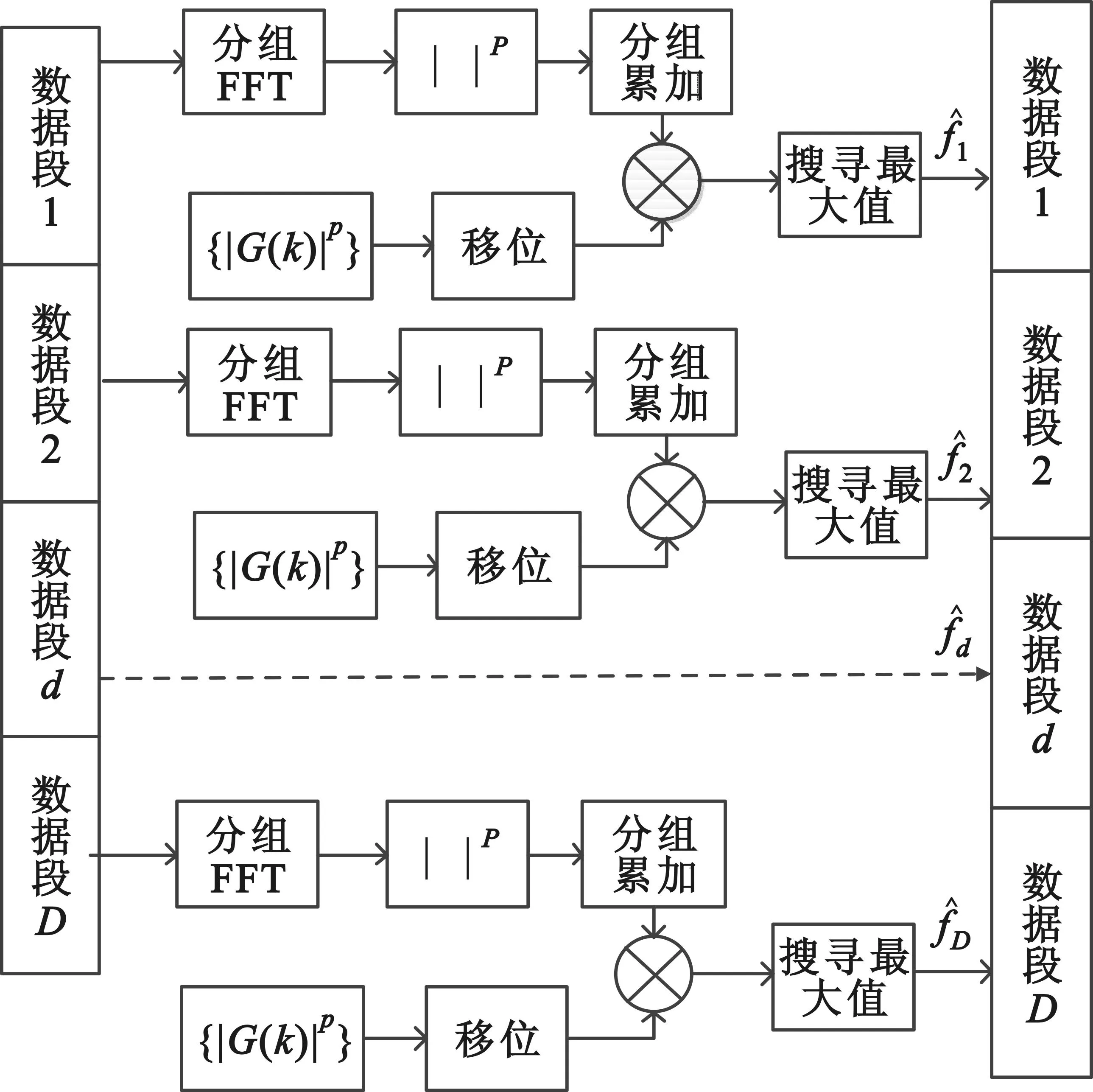
图3　针对高动态环境改进的分段累加FFT算法实现框

4仿真分析

仿真在S频段中实现，载波频率设为2 GHz，利用频偏估计方差来表征算法的估计精确度。信号采用了每符号5样点的采样率采样，符号速率为2 400 b/s，观察区间为8 192个符号，按照每段510符号长度进行分段FFT。

仿真环境如图2所示，采用初速度1马赫，加速度5 g，此时信号的多普勒频率k0=2 266.67 Hz，多普勒一阶变化率k1=333.33 Hz/s。图4为传统算法在高动态环境下的归一化频偏估计方差仿真图，比较了不同p值的频偏估计方差，从图中可以看出，在低信噪比环境下p=1/2时系统性能最好。因此在后续仿真中均采用p=1/2。

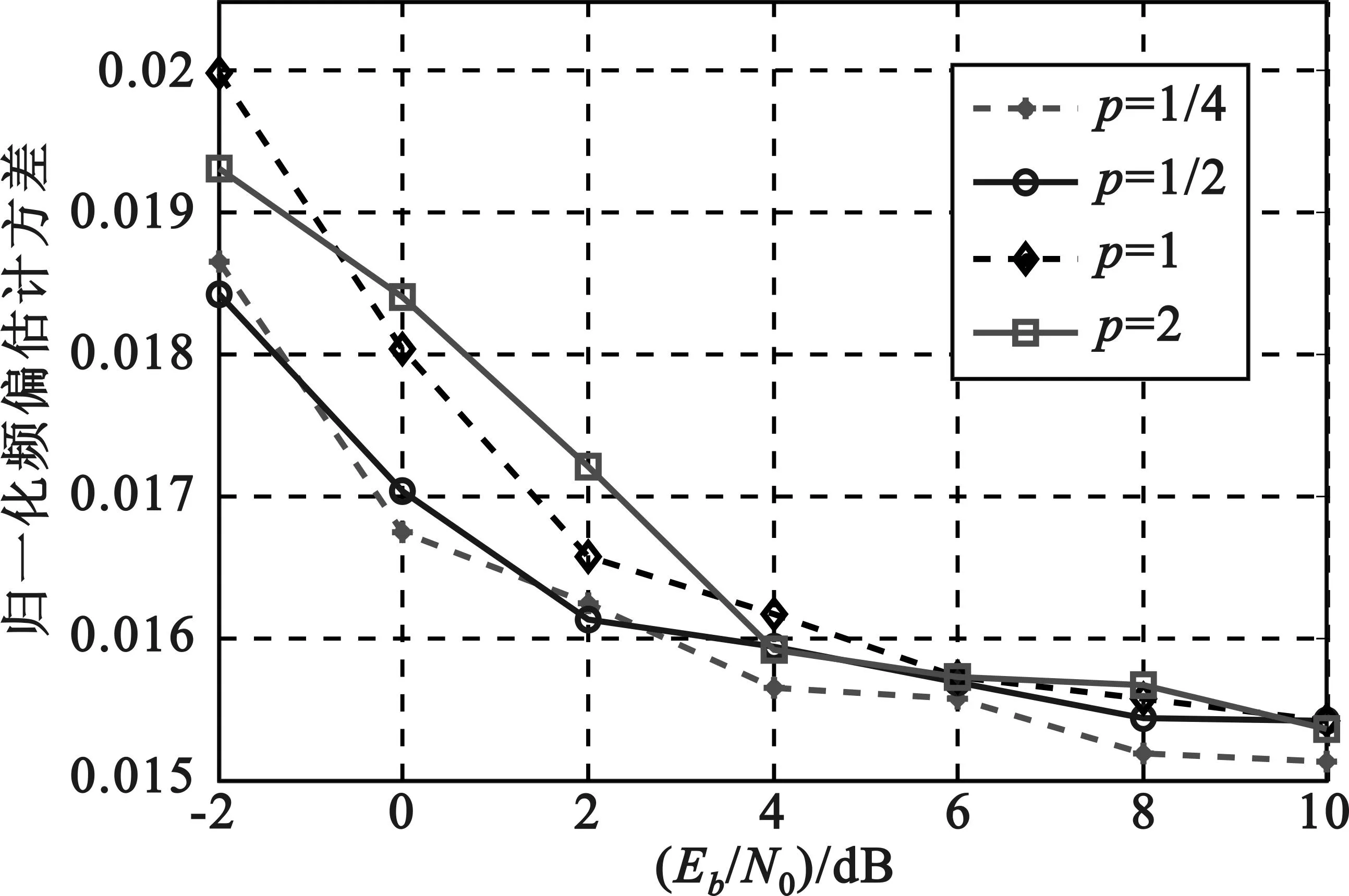
图4　传统算法的归一化频偏估计方差

图5是改进前后两种算法在初速度为1马赫，加速度不同的条件下归一化频偏估计方差变化图。其中，改进算法在仿真中将数据分为两组，图中所示为第一组数据的归一化频偏估计方差图；每组数据的归一化频偏估计方差分别是通过下式计算得出：

(18)

从图中可以看出当加速度小于1 g时，传统算法得到的频偏估计值相较于改进后的算法准确度更高，当加速度大于1 g时，改进后的算法准确度相较传统算法准确度提高了将近50%。可见改进后的算法相较于传统算法更适合高动态环境。

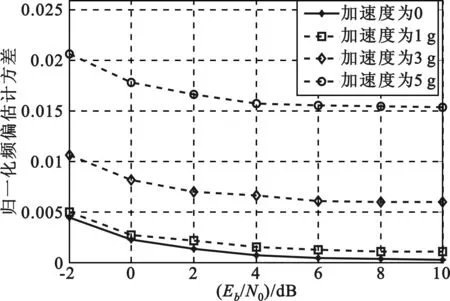
(a)传统算法

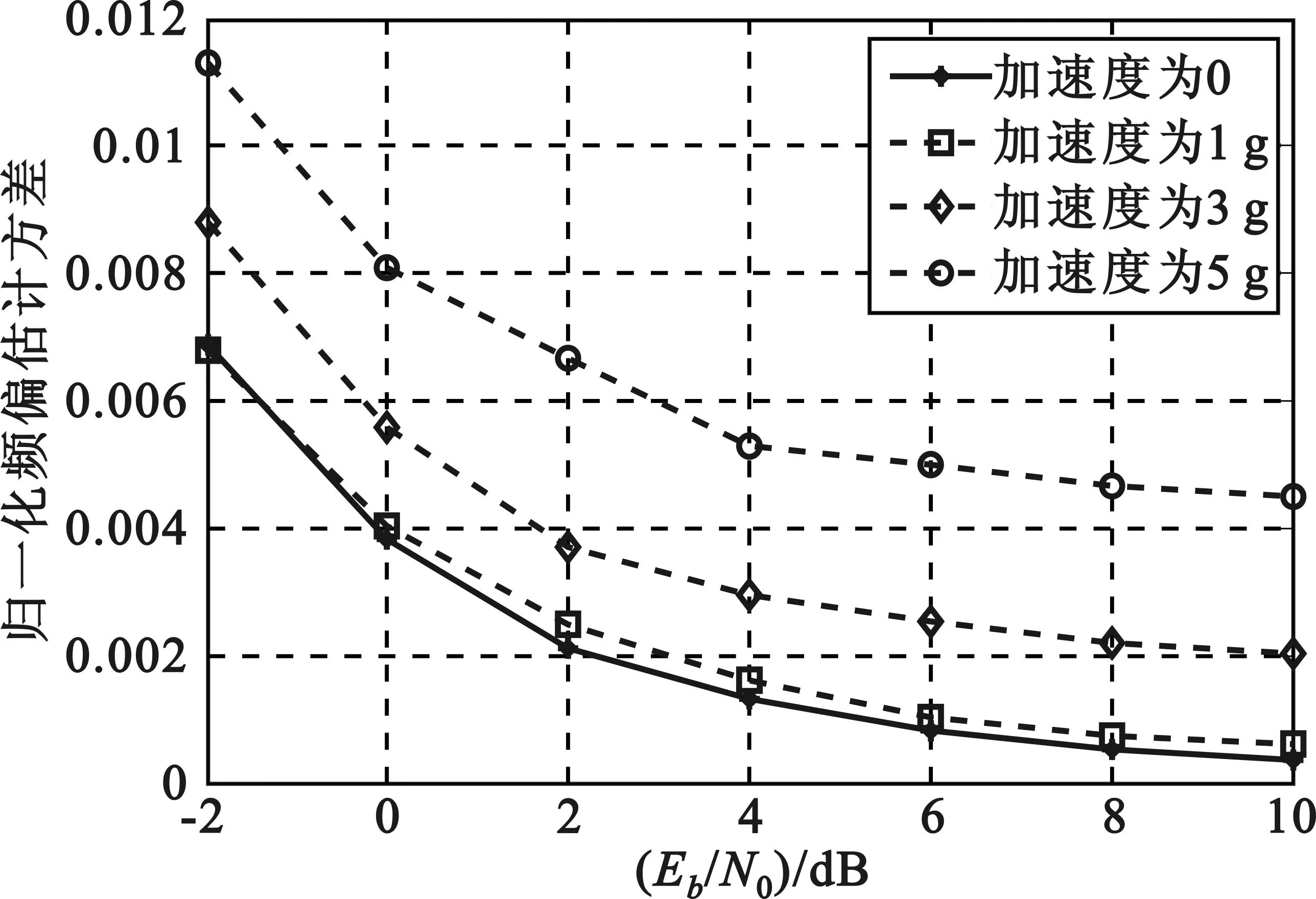
(b)改进算法

图6是改进算法中将数据分为两组，每组数据各自归一化频偏估计变化图。从仿真图可以看到改进后的算法仿真中，数据分为两组时，在Eb/N0=0 dB处，第一组的频偏估计方差比未分组的频偏估计方差小了近50%，说明分组后的第一组数据的频偏估计值的准确度提高了近50%；第二组的频偏估计方差与未分组的频偏估计方差大了近50%，但是在计算频偏估计方差时是与初始时刻的频偏值进行比较，所得归一化频偏估计方差越大说明该估计值距离频偏初值越远，而这正好符合图2所示的频偏变化规律：频偏随着时间的增加变大。因此第二组的频偏估计值的准确度仍然很高。

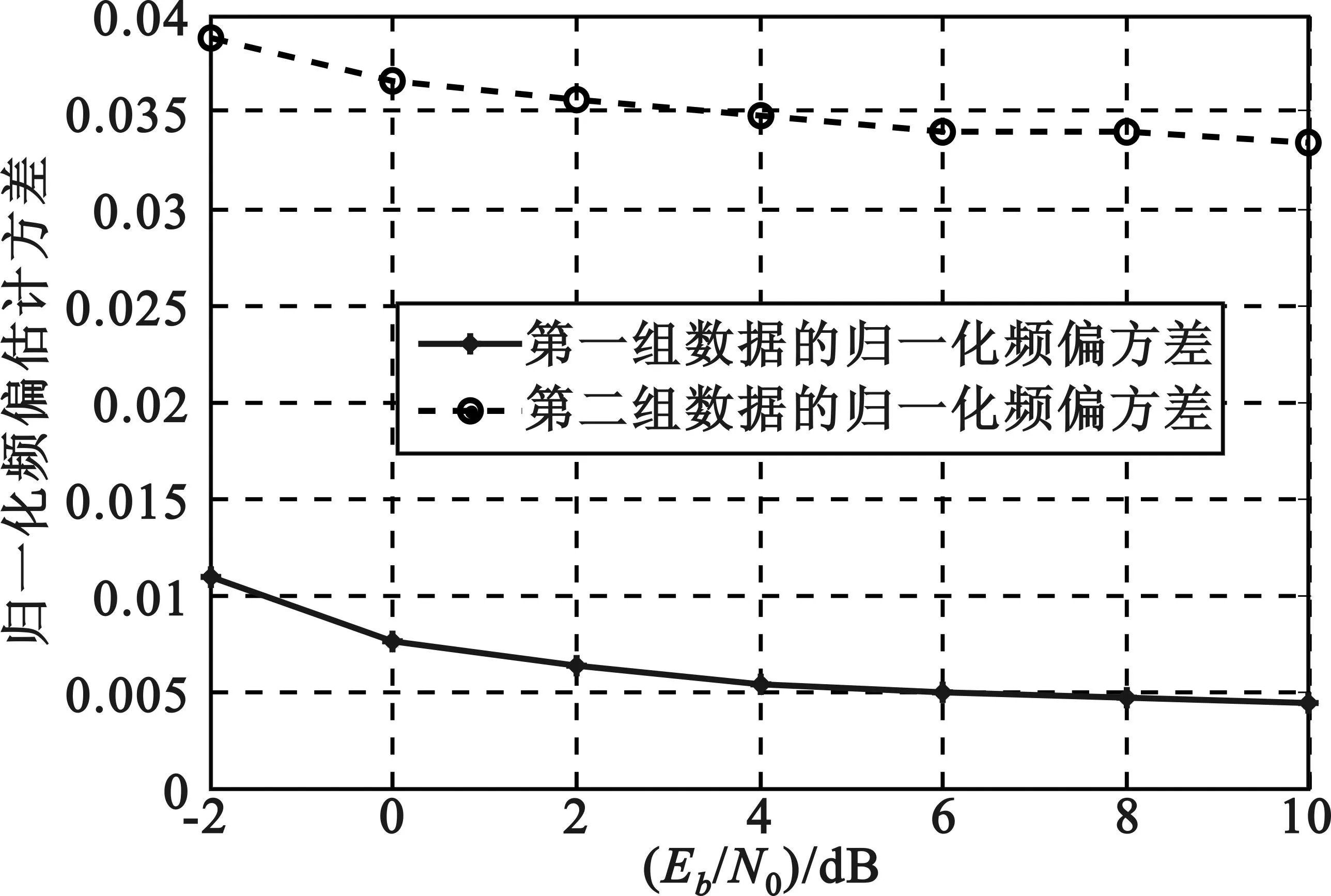
图6　改进算法后分为2组的归一化频偏估计方差

图7和表2分别是采用初速度1马赫，加速度5 g的仿真环境下改进算法所得信号归一化频偏一阶变化率估计方差变化图和频偏一阶变化率均值信息。可以看到改进后的算法可以得到信号的频偏一阶变化率，并且准确度较高。表2所得频偏一阶变化率估计值与实际一阶频偏变化率k1相差不大，信噪比越高，估计的准确度越高。

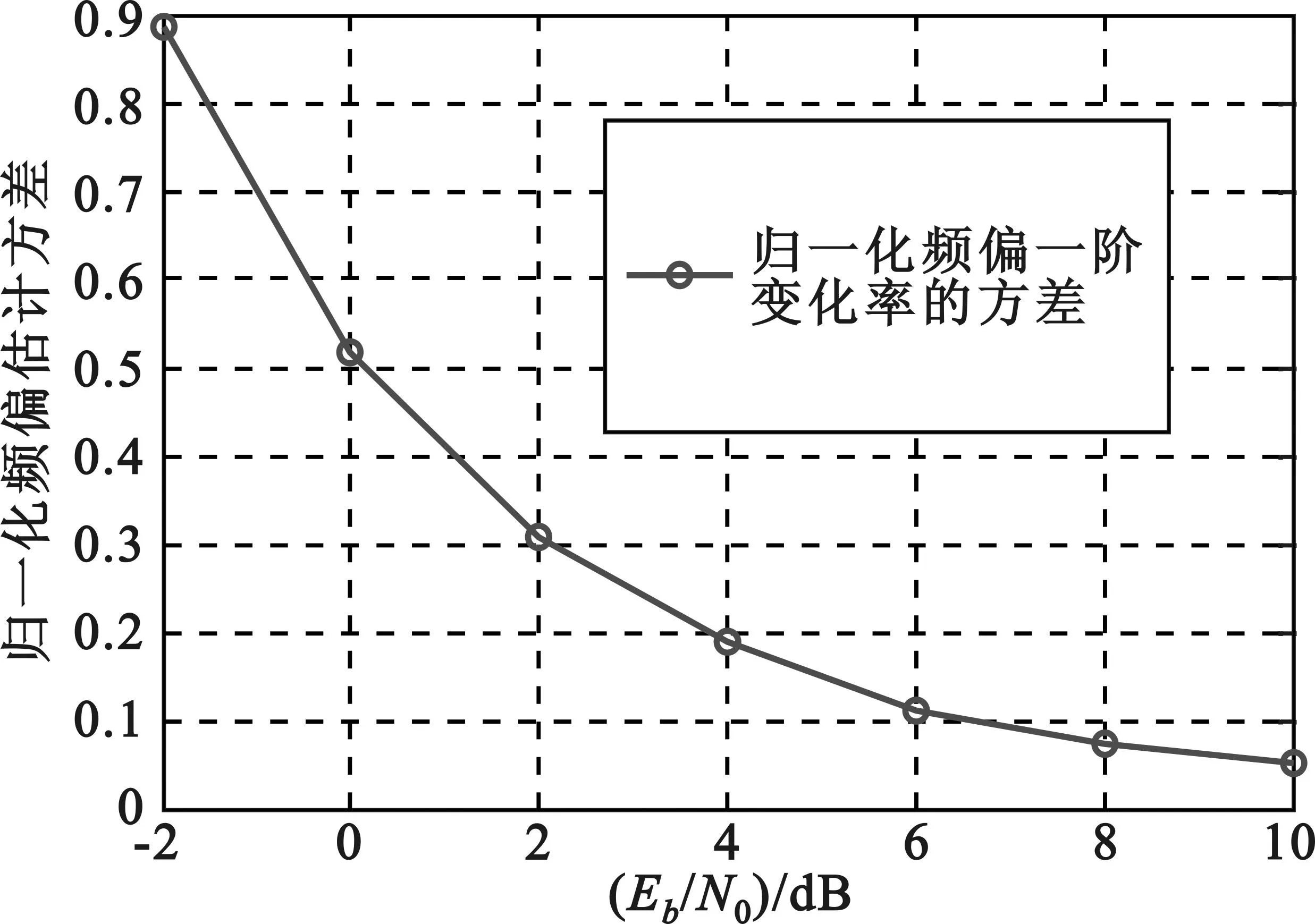
图7　分为2组的归一化频偏一阶变化率估计方差

信噪比-2dB0dB2dB4dBk316.254332.583326.933331.839

5结语

本文针对信号在高动态环境下存在很大多普勒频偏以及高阶多普勒变化率的问题，在传统分段累加FFT粗估算法的基础上进行了优化创新。首先将接收数据分组，并分别对每组数据的频偏值利用分段累加FFT算法进行粗估计，并通过差分计算求出对应的频偏变化率，最后将每组频偏的粗估值及频偏变化率的粗估值补偿到该段数据中，以方便后续进行更为精细的同步估计工作。相比于传统分段累加FFT粗估算法，改进后的算法的估计精度有了显著提高，并且可以得到相应的频偏变化率，本文提出的新方法对高动态环境下的频偏粗估具有很强的针对性，具有一定的实用价值。

参考文献：

[1]贾鹏,吴团峰,胡卓宇等.高动态短时突发扩 频信号的快速捕获[J].通信技术,2015,48(06):657-661.

JIA Peng, WU Tuan-feng, HU Zhuo-yu, et al. Fast Acquisition of Hign Dynamic and Short-Term Burst Spread Spectrum Signal[J].Communications Technology. 2015, 48(06): 657-661.

[2]Mengali U, Andrea A N. Sychronization Techniques for Digital Receivers[M]. New York: Plenum, 1997.

[3]龚超, 张邦宁, 郭道省. 基于FFT的快速高精度载波参数联合估计算法[J]. 电子学报, 2010, 4(04):766-770.

GONG Chao, ZHANG Bang-ning, GUO Dao-xing. A Quick and Accurate Union Carrier Parameter Estimition Algorithm based on FFT. Acta Electronica Sinica, 2010,4(04):766-770.

[4]Mazzenga F, Corazza G. Blind Least-Squares Estimation of Carrier Phase, Doppler Shift, Doppler Rate for M-PSK Burst Transmission[J].IEEE Trans Lett,1998,2(3):72-75.

[5]Richard G Lyons. Undersanding Digitial Signal Processing[M].Second Edition.Beijing：CMPEDU,2005.92-94.

[6]叶展,张超,潘小飞等.基于分段FFT累加的大频偏估计算法[J].军事通信技术，2012,33(04):97-100.

YE Zhan, ZHANG Chao, PAN Xiao-fei, et al. Large Frequency-Offset Estimator based on Accumulation of FFT’s Rusults[J]. Journal of Military Communications Technology. 2012, 33(04): 97-100.

[7]Vilnrotter V A, Hinedi S, Kumar R. A Comparison of Frequency Estimation Techniques for High-Dynamic Trajectories[J]. Nasa Sti/recon Technical Report N, 1988, 89(4):559-577.

[8]王晓湘,柯有安.高动态多普勒频率的最大似然估计器[J].北京邮电大学学报,2000,23(01):61-65.

WANG Xiao-xiang, KE You-an. Maximum Likelihood Estimation of High Dynamic Doppler Frequency[J].Journal of Beijing University of Posts and Telecommunications, 2000, 23(01): 61-65.

王雅慧(1991—)，女，硕士研究生，主要研究方向为卫星通信；

叶展(1978—)，男，博士，讲师，主要研究方向为卫星通信、通信信号处理、同步技术等；

郭道省(1973—)，男，博士，主要研究方向为卫星通信、通信抗干扰、信号处理等；

杨晗竹(1991—)，女，硕士研究生，主要研究方向为卫星导航、卫星通信等。

A Modified Coarse Frequency Offset Estimation Algorithm in Highly Dynamic Environment

WANG Ya-hui，YE Zhan，GUO Dao-xing，YANG Han-zhu

(College of Communication Engineering,PLA University of Science & Technology,Nanjing Jiangsu 210007,China)

Abstract：Aiming at the Doppler shift even frequency acceleration and high order acceleration resulted from high-speed movement, an optimized method, based on the accumulation of FFT algorithm in frequency estimating under high dynamic environment is proposed. Firstly, the algorithm divides the received data into groups, and then the frequency-offset of each group is estimated by using accumulation FFT algorithm. The experimental results show that this modified algorithm could acquire a fairly high accuracy of about 50% in estimating frequency-offset, and this is quite applicable for frequency-offset estimation in highly dynamic environment.

Key words：highly dynamic environment; coarse estimation; FFT

作者简介：

中图分类号：TN927.2

文献标志码：A

文章编号：1002-0802(2016)01-0024-05

*收稿日期：2015-08-01；修回日期：2015-11-26Received date:2015-08-01；Revised date：2015-11-26

doi:10.3969/j.issn.1002-0802.2016.01.005