概率论与数理统计教学在高校新专业设置下的探讨

沈　燕，徐　蓉，鹿亚梅，史　悦

(安徽大学　数学科学学院，合肥　230601)



概率论与数理统计教学在高校新专业设置下的探讨

沈燕，徐蓉，鹿亚梅，史悦

(安徽大学数学科学学院，合肥230601)

摘要：近年来很多高校开设了金融数学专业，该专业致力于培养能够应用金融数学的工具解决实际问题的人才。概率论与数理统计是金融数学专业的核心课程，而且也是许多其他后续课程的基础，在课程教学体系中占有重要的地位。结合教学实践，讨论了概率统计中的重要概念和实验教学的方法，目的在于引导学生具备探究问题本质及学以致用的能力。

关键词:概率统计；条件期望；实验教学；金融数学

概率论与数理统计是研究随机现象的统计规律性的一门学科，是数学学院的主干课程。该课程的教学不仅要向学生传授随机现象及其规律性，更重要的是对学生统计思想和统计意识的培养。金融数学学科是从20世纪80年代才开始出现的一门学科[1]，是在两次华尔街革命的基础上迅速发展起来的数学与金融学相结合的交叉学科，它主要是以概率统计和泛函分析为基础，随机分析及鞅理论为核心，研究金融等定量分析，探求金融工具的内在规律，并用来解决实际问题。金融数学与我国的金融改革和发展有紧密的关系，在我国的发展前景不可限量。因此，近年来很多高校开设了金融数学专业[2]。概率论与数理统计是金融数学专业的核心课程，而且也是许多其他后续课程，如运筹学，证券金融学，随机过程，金融风险管理等课程的基础，在课程教学体系中占有重要的地位。随着社会经济的发展和科学技术的进步，概率论与数理统计的研究领域不断扩展，研究内容也日益更新。为了适应学科的发展及高校专业设置的变化，概率统计的教学也应被赋予新的内容和形式[3]，在课堂教学中强调不同知识的内在联系，激发学生自己寻求解决方案的热情。在学生通过自己的思考，解决问题的过程中，学生能从更高的角度理解知识的内涵，实现从理论到应用，而不是生硬的从概念到理论的教学实践过程，提高学生的分析问题和解决问题的能力。

1对条件概率和条件数学期望的理解

现代概率论一般从讲述条件期望开始，这是由于以测度论为基础的条件期望是鞅论的基础，也是严格阐述现代概率论必不可少的基本概念[4]。随着人们对随机现象研究的不断深入，条件数学期望的概念被广泛的应用到实际问题中，条件数学期望在运筹学、金融领域等得到广泛应用，例如条件期望在最优预测、期权定价模型等问题中的应用。因此对条件概率和条件期望的学习是金融数学专业学生必要的知识准备。

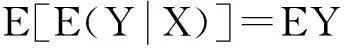
(1)

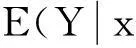
极值理论是研究次序统计量极端值分布特性的理论，是次序统计理论的一个分支，1943年Gnedendo建立的极值定理为该理论的基础，极值定理认为极值的极限分布与本身的分布是独立的。Gumbel于1958年对极值理论研究作出系统总结，从而形成了极值理论。极值理论可应用在研究国债期货合理涨跌停板的设计中，是测量极端市场条件下风险损失的一种重要方法，具有超越样本数据的估计能力，并且可以准确地描述分布尾部的分位数。它主要包括了两类模型：BMM 模型和POT模型，由于金融时间序列常常具有波动聚集特征，而使用区组最大值法有可能会漏掉一些有用的数据，因此人们更倾向于使用POT模型，即超越阈值方法。而POT模型的理论基础就是我们本科阶段概率统计课程所学的条件数学期望概念。

例1[5]假设序列{zt}的分布函数为F(x)，定义Fu(y)为随机变量Z超过阈值u的条件分布函数，它可以表示为：

Fu(y)=P(Z-u≤y|Z>u)y≥0

利用条件概率公式可以得到：

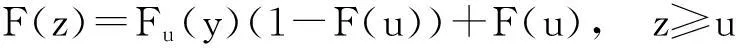
(2)

Pickands[6]于1975年证明了以下结论。

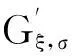
(3)

根据(3)式可以得到，对于给定的一个符合广义的帕累托分布的样本{z1,…,zn}的对数似然函数L(ξ,σ|z)为：

(4)

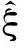
F(z)=Fu(y)(1-F(u))+F(u)=

2将数理统计思想融入教学改革中

概率统计是一门非常贴近生活适用性很强的一门学科，将概率统计的教学与数学软件有机的结合起来，解决实际问题，有效的调动学生的学习积极性。目前常用的统计软件有SPSS，SAS和R等，而除了这些常用的统计软件之外，Excel软件的操作简单，功能强大，通俗易懂，可以作为概率统计实验教学的内容。而且统计软件课程的开设是在学过数理统计课程之后，我们在数理统计教学中运用简单直观的Excel进行演示，加深学生对数理统计课程的直观认识，通过excel实现绘图、数据分析和数值计算等，在演示和实验过程完成教学内容，使概率统计的课堂教学生动具体，提高学生的学习兴趣。

例如，在讲述方差分析的时候，常常遇到两个因素同时可能影响试验结果的情形，称为双因素方差分析，如果除了这两个因素的单独影响，两个因素的搭配还会对试验结果产生一种新的影响，即为有有交互作用的双因素方差分析。在讲述有交互作用的双因素方差分析时，可以用Excel向学生演示分析结果，加深对方差分析问题直观的认识。

例3为分析4种化肥和3种农作物品种对农作物产量(单位：Kg)的影响，把一块试验田等分为24小块，对种子和化肥的每一种组合种植两小块田，得到产量如下表，试分析化肥，农作物品种及二者的交互作用对农作物产量有无显著影响(显著性水平α=0.05)。

化肥1化肥2化肥3化肥4品种1153152154156152153159160品种2155153158159154155156154品种3151151153154152150150149

针对问题我们提出的原假设是：

H0A：农作物品种对产量无显著影响，

H0B：化肥对产量无显著影响，

H0AB：农作物品种和化肥的交互作用对产量无显著影响。

由图1可见，检验品种因素(行因素)的统计量FA=43.957>FAα=3.885,说明品种因素对产量的影响是显著的。检验化肥因素(列因素)的统计量FB=15，对应的P值=0.000231，小于显著性水平0.05，说明化肥因素对产量的影响是显著的。同样由图1可以认为品种与化肥种类的交互因素对产量的影响也是显著的。因而应该注意化肥与农作物品种的交互作用，从试验数据看，化肥4与品种1的搭配产量最高，因此可以考虑把二者搭配起来安排生产。

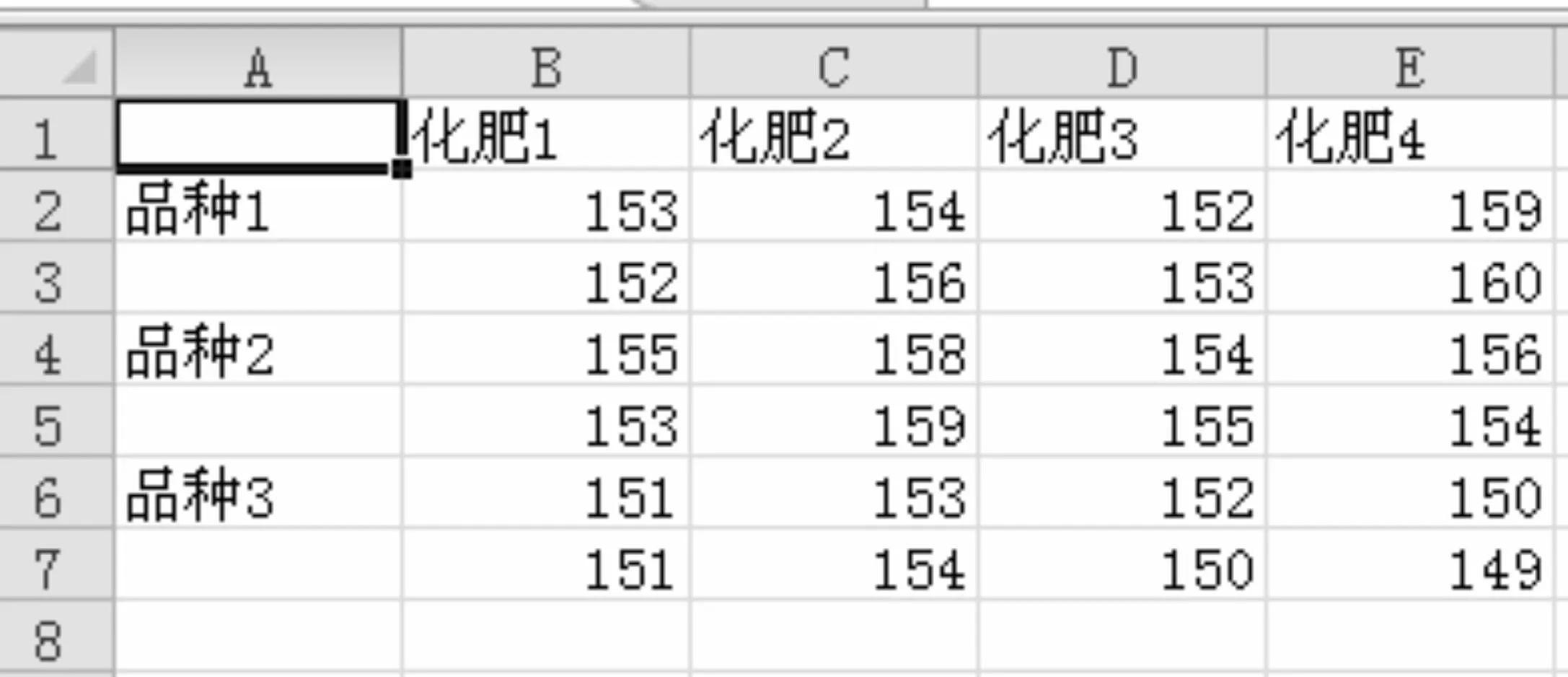
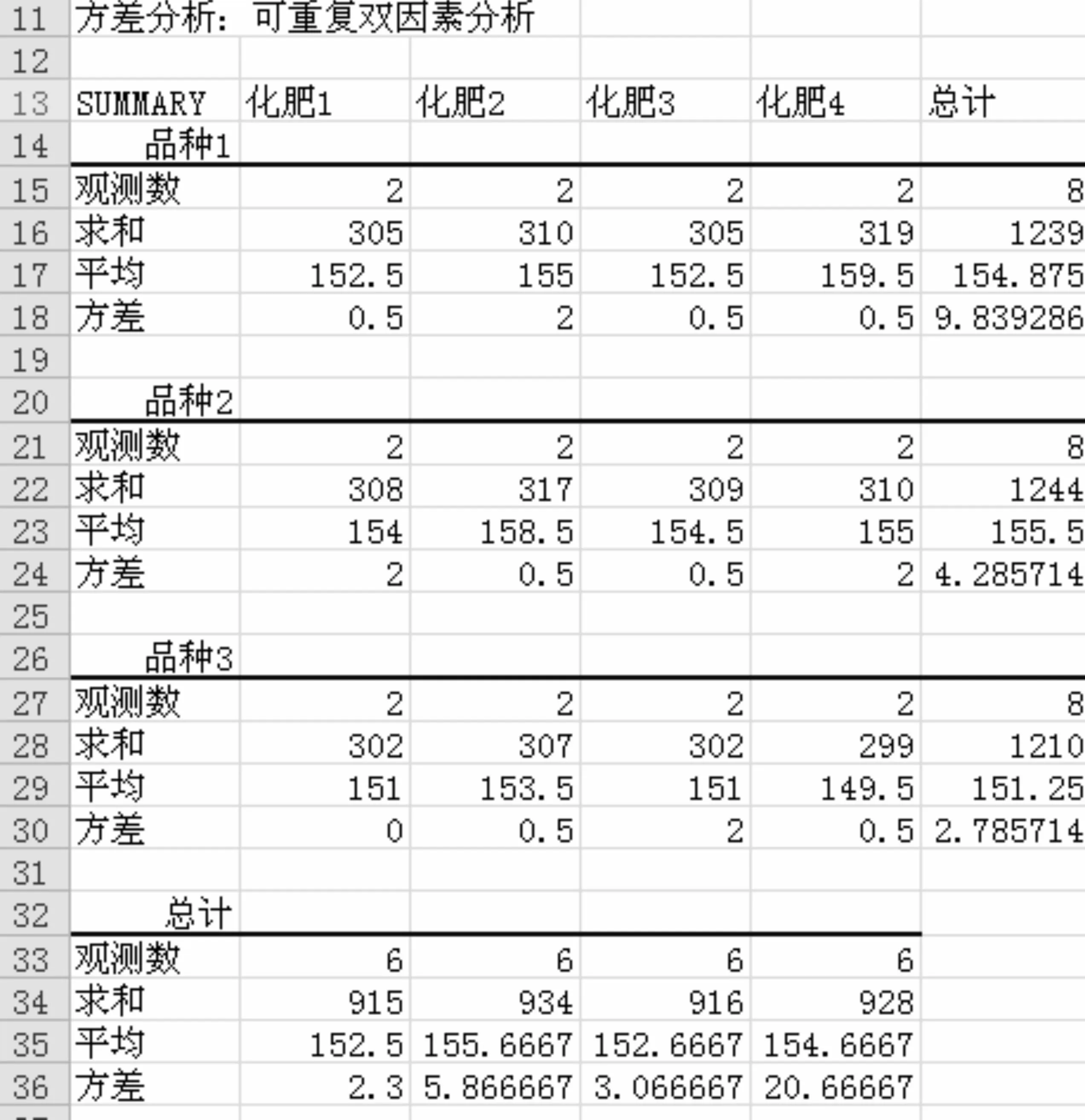
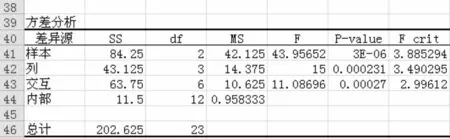
图1

随着社会的进步，经济的发展，高校专业设置也在不断的调整，使之更加顺应时代的需求、市场的需求。这也要求我们的概率统计教学，不能只关注概率统计的基本概念，公式和方法的介绍，我们要站在更高的角度去引导学生，启发学生去思考概率统计理论方法产生的实际背景，这些理论和方法的优缺点是什么。逐步引导学生摒弃死记硬背概率统计基本原理和结论的学习方法，充分调动学生的主动性，探究问题的本质，并将这些方法应用到实际问题中，解决具体问题，达到学以致用的目的，实现理论和观点的创新。

参考文献：

[1]严加安.金融数学引论[M].北京：科学出版社，2012：38.

[2]刘永辉，方勇，沈春根.金融数学专业人才培养模式的改革与探讨[J].上海金融学院学报，2012(5): 114-120.

[3]姜礼尚，徐承龙．金融数学课程体系、教材建设及人才培养的探索[J]．中国大学教学，2008(10)：11-13.

[4]严加安．测度论讲义[M]．北京：科学出版社，2004：44.

[5]郑振龙,王保合.基于极值理论的风险价值度量[J],金融学季刊,2005(1):65-80.

[6]Pickands J.Statistical Inference Using Extreme order Statistics[M].Ann Statist,1975:119-131.

[责任编辑：张永军]

Discuss the Probability and Statistics Teaching Based on New Major of University

SHEN Yan, XU Rong, LU Ya-mei, SHI Yue

(School of Mathematical Sciences, Anhui University, Hefei 230601，China)

Abstract:Financial Mathematics is set up in many universities in recent years in order to train talents who can solve practical problems by using financial mathematics.Probability and statistics is a professional core course for these students who major in financial mathematics.And it is a basic course of other core courses.It plays an important role in the whole curricular system.In this paper, some important concepts and methods of experimental teaching are discussed based on the teaching practice.Our main purpose is to induct student to explore the nature of the problem in the teaching process.

Key words:probability and statistics; conditional expection; experimental teaching; financial mathematics

中图分类号：G642.0

文献标识码：A

文章编号：1673-162X(2016)01-0131-04

作者简介：沈燕(1976—)，女，安徽利辛人，安徽大学数学科学学院副教授，博士，硕士生导师。

基金项目：安徽省高等学校自然科学研究项目(KJ2015A065)、安徽大学博士科研启动基金、安徽省质量工程项目(2015jyxm054)、安徽大学科研训练计划项目(KYXL2014015、KYXL2014013、KYXL2014016)、安徽大学本科教育质量提升计划项目(xjjyxm14022、XJYYKC1401、ZLTS2015053)资助。

收稿日期：2015-12-20修回日期：2016-01-08