基于多轴疲劳理论的曲轴结构等效疲劳研究
孙嵩松,俞小莉,李建锋
(1.浙江大学动力机械及车辆工程研究所,杭州 310027; 2.潍柴动力杭州分公司,杭州 310012)
2016157
基于多轴疲劳理论的曲轴结构等效疲劳研究
孙嵩松1,俞小莉1,李建锋2
(1.浙江大学动力机械及车辆工程研究所,杭州 310027; 2.潍柴动力杭州分公司,杭州 310012)
采用有限元法,对曲轴进行弯矩载荷作用下的应力分析,并应用坐标变换法对应力集中区域内的应力状态进行分析,确定曲轴的临界平面位置和疲劳损伤的类型。在此基础上选择合适的多轴疲劳损伤模型对由同种材料、不同结构的曲轴的疲劳极限载荷进行预测。预测与试验结果对比表明:传统的名义应力法在预测同种材料、且圆角半径相同的曲轴疲劳极限载荷时具有较高的准确度,但是在预测不同圆角的曲轴的疲劳极限载荷时,误差较大;而采用经典的KBM多轴疲劳损伤模型,能有效准确地预测不同圆角的曲轴的疲劳极限载荷。
发动机曲轴;多轴疲劳损伤模型;临界平面;疲劳极限载荷
前言
曲轴等发动机零部件在实际工作过程中,一些关键部位如圆角、油孔等由于截面形状的突变,会产生应力集中现象,往往是导致疲劳失效的来源[1]。
针对该类问题,近年来国内外的一些学者做了大量的工作。其中Taylor提出了裂纹模拟技术,通过构造与构件应力梯度一致的标准裂纹体,对同样材料属性、不同结构的构件的疲劳极限载荷进行预测,但是由于二者之间应力状态的本质差异,预测结果有时会导致较大的误差[2-5];同时Taylor提出了临界距离理论,通过对一定范围内的应力状态进行分析,取得了更为准确的疲劳极限预测结果[6-8]。
国内方面,文献[9]中利用Isight平台,定量分析了曲轴主要的结构参数对其疲劳强度的影响,并与试验结果进行了对比;针对传统裂纹模拟技术的不足,文献[10]中提出了利用等效缺口件预测曲轴的疲劳极限载荷,取得了更准确的预测结果;文献[11]和文献[12]中采用多体动力学计算了曲轴和轴承座在循环工况内的复合载荷作用下的疲劳寿命,取得了更具指导意义的结论。
与国外的研究相比,目前国内针对发动机零部件疲劳的研究,大部分还都是基于传统的名义应力法,即认为曲轴的疲劳寿命与应力集中处的应力幅值呈对数线性关系。该方法在一般工程应用中,能够比较方便地对零部件的安全性进行评估,但是通常将应力集中处的应力状态,默认为是单轴的拉伸应力状态。对于曲轴这样的三维实体构件,其在外载作用时,应力状态往往呈现出一定的多轴性,因此这种假设往往与实际的情况存在一定的偏差。据此,本文中首先根据曲轴应力集中处的应力状态分析,判断曲轴的损伤类型,在此基础上对同种材料、同种工艺的曲轴的疲劳极限载荷进行预测。通过对比预测与试验结果证明,与传统名义应力法相比,基于多轴疲劳理论的方法能更准确地预测不同结构曲轴的疲劳极限载荷。
1 曲轴损伤类型分析
1.1 基本损伤模型
目前针对多轴疲劳的问题,还没有一个通用的损伤模型。研究表明[13-15],临界平面法能够较为准确地预测多轴疲劳寿命。其主要流程分为两步:第一,基于某一准则确定临界平面;第二,基于确定的临界平面,采用相应的疲劳损伤模型进行疲劳寿命的研究。
根据构件材料类型和应力集中处的应力应变状态,可将金属构件的破坏分为拉伸型和剪切型两种疲劳破坏形式[16]。对于拉伸型破坏,Smith认为应力集中处的裂纹扩展垂直于最大拉伸应变方向,因此临界平面就定义为最大正应变幅平面[17];而对于剪切型的破坏,Eatemi认为裂纹沿着最大剪切应变方向扩展[18]。因此通过对曲轴应力集中处的应力应变状态进行分析,便可确定最大拉伸应变和最大剪切应变的方向。在此基础上再与实际试验中曲轴裂纹扩展的方向进行对比,即可确定破坏形式。
1.2 最大应力应变平面的确定方法
对于曲轴这样的三维实力构件,其应力集中处的应力应变状态往往比较复杂,其最大应力应变平面的确定,可以采用应变张量矩阵结合坐标系变换法[19-20]。该类方法的第一步,就是以空间任意一点O为原点建立坐标系O-XYZ,如图1所示。
图中,平面Δ是空间中通过O点的任意平面,其法向向量为n,n在O-XYZ坐标系中的投影与X轴、Z轴的夹角分别为θ和φ,O点的应变张量在O-XYZ坐标系中的矩阵表达式为
(1)
引入如图1所示坐标系O-nab,则法向向量n与a和b轴在O-XYZ坐标系下的表达式分别为
(2)
(3)
(4)
对于平面Δ中,过O点的任意方向的直线m,m与O-nab坐标系中a轴之间的夹角为α,如图1所示,则沿m方向的向量为
(5)
则对于平面nom内的剪切应变张量和向量n方向的拉伸应变张量分别为
(6)
(7)
通过改变α,θ和φ的值,分别计算出各个平面内的剪切应变、拉伸应变的最大值,就可以确定拉伸应变最大与剪切应变最大的平面。通过对比该平面与实际裂纹扩展面,即可确定疲劳破坏的形式。
1.3 曲轴应力应变状态及其破坏形式分析
根据曲轴的结构特点,选取其中某一曲拐作为应力应变的计算对象,图2为某款发动机曲轴某一曲拐的有限元模型,根据圣维南原理,曲轴的边界条件可等效为在曲轴的右主轴颈端面约束住所有的自由度,曲轴的弯矩载荷施加在左截面,载荷大小为任意载荷,弯矩载荷作用下曲拐应力分布的计算结果如图3所示。
由图3可以看出,曲轴在受到弯矩载荷的作用时,最大应力值在曲柄销的圆角部位。为保证疲劳寿命的预测精度,对曲轴圆角部位应力状态计算结果的网格依赖性进行分析[21],其结果如表1所示。

表1 曲轴圆角应力与网格尺寸的关系
由表1可以看出,当曲轴圆角处的网格尺寸由1.5减小至1.0mm时,最大应力值相对增幅不足1%,由1.0减小至0.5mm时,相对增幅不足0.5%,说明此网格尺寸下的应力值已经趋收敛于确定值。综合考虑计算精度和成本,最终网格尺寸确定为1.0mm。
利用坐标变换法对曲轴应力集中处的应力状态进行分析,最终得出最大剪切应变所在的平面内的α,θ和φ值分别为136°,90°和91°,而最大拉伸应变平面内的α,θ和φ值分别为0°,90°和0°。
在曲轴弯曲疲劳试验中,裂纹扩展的路径是由曲柄销的圆角部位指向主轴颈的圆角部位。裂纹扩展所在的平面,与曲轴轴线约成135°的夹角。对比分析计算所得的结果,可以确定曲轴的疲劳属于剪切型疲劳。
2 曲轴算例
2.1 疲劳模型与预测方法
对于多轴疲劳问题,目前还没有一个真正意义上通用的寿命预测模型。早期开展的多轴疲劳研究大多是针对低周疲劳进行的,其加载控制方式主要采用应变控制。而曲轴的疲劳属于典型的高周疲劳问题,与仅仅采用应变状态来描述疲劳破坏与损伤的物理机理有差别。Brown和Miller根据疲劳损伤力学相关理论,认为临界平面内的剪切应变是裂纹萌生和形成的主要因素,同时法向应变控制着裂纹的扩展与增长速率。在此基础上Kandil提出了著名的KBM模型,用于分析剪切疲劳问题[22]。该模型综合考虑了应力应变状态对多轴疲劳的影响,其表达式为
(8)
式中γmax和εn,max分别为临界平面内的剪切应变与法向拉伸应变。
本文中所研究的曲轴材料为42CrMo,该材料的屈服极限为930MPa。而在试验过程中,曲轴圆角应力集中处应力值最大为680MPa,因此假设只包括弹性应变,则式(8)可简化为
(9)
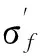
log(εeq)=blog(2Nf)+A
(10)
在实际工程应用中,对于同种材料、同种工艺的曲轴,其材料属性均可作一致性处理,因此A和b可以认为是定值。因而对于相同材料、相同工艺制造的曲轴,其疲劳寿命可认为仅取决于εeq。因此,依据某已知疲劳极限载荷值的曲轴的基础数据,则可预测其他与之有着相同材料、相同工艺曲轴的疲劳极限载荷,具体流程为:
(1) 对已知极限载荷的曲轴进行有限元分析,并对圆角应力集中处的应力状态进行分析,获取其极限等效应变;
(2) 对同种材料、同种工艺的曲轴在一定弯矩载荷下的有限元分析,计算其等效应变;
(3) 通过对比等效应变结果,预测曲轴的疲劳极限载荷。
2.2 曲轴预测案例及其分析
选取已有试验数据的某一型号C0曲轴为例,对其进行等效应变的计算。该曲轴的材料为42CrMo,表面氮化。通过对试验数据进行统计分析,可得到该型号的曲轴的疲劳极限载荷为4 882N·m。通过有限元分析,在该弯矩载荷作用下,曲轴圆角应力集中处的Mises应力最大值为557MPa,临界平面内的应力应变分量如表2所示,载荷比为-1,代入式(11)计算,可得其在极限等效应变为0.002 922 7。
选取其他两款与上述曲轴具有相同的材料和工艺的曲轴C1和C2,对其施加1 000N·m的弯矩,其应力集中处的最大应力分别为133和210.5MPa,应力应变状态的分析结果如表2所示。
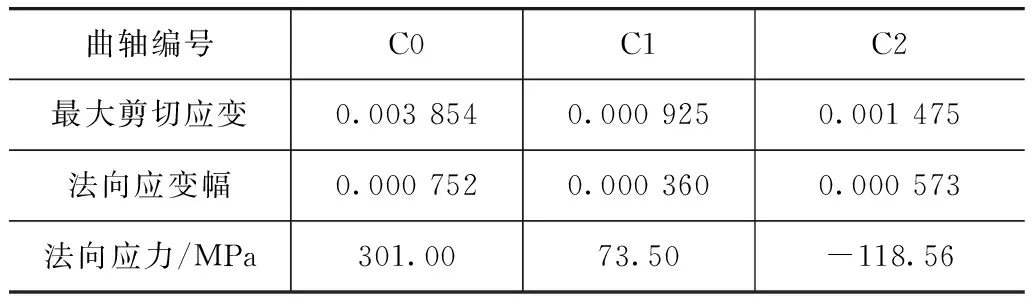
表2 曲轴应力应变状态
设C1和C2曲轴的疲劳极限载荷分别为X1和X2,基于KBM模型求解其疲劳极限载荷,则有
Δεn1=0.0029227
Δεn2=0.0029227
解方程得:X1=4284N·m;X2=3323N·m。采用基于传统的名义应力法求解上述这两款曲轴的疲劳极限载荷,则有:
3 疲劳试验验证
采用机械谐振式曲轴弯曲疲劳试验装置,对曲轴进行弯曲疲劳试验。试验过程中载荷的控制和失效判定可参照文献[23]和文献[24]。表3和表4为这两种曲轴的疲劳试验数据。
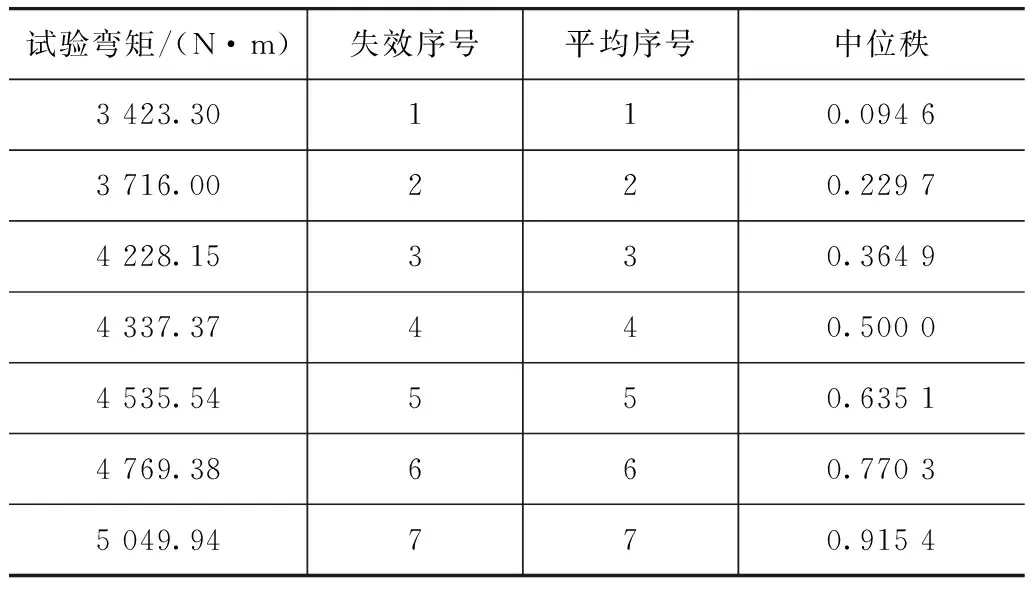
表3 C1曲轴疲劳试验数据
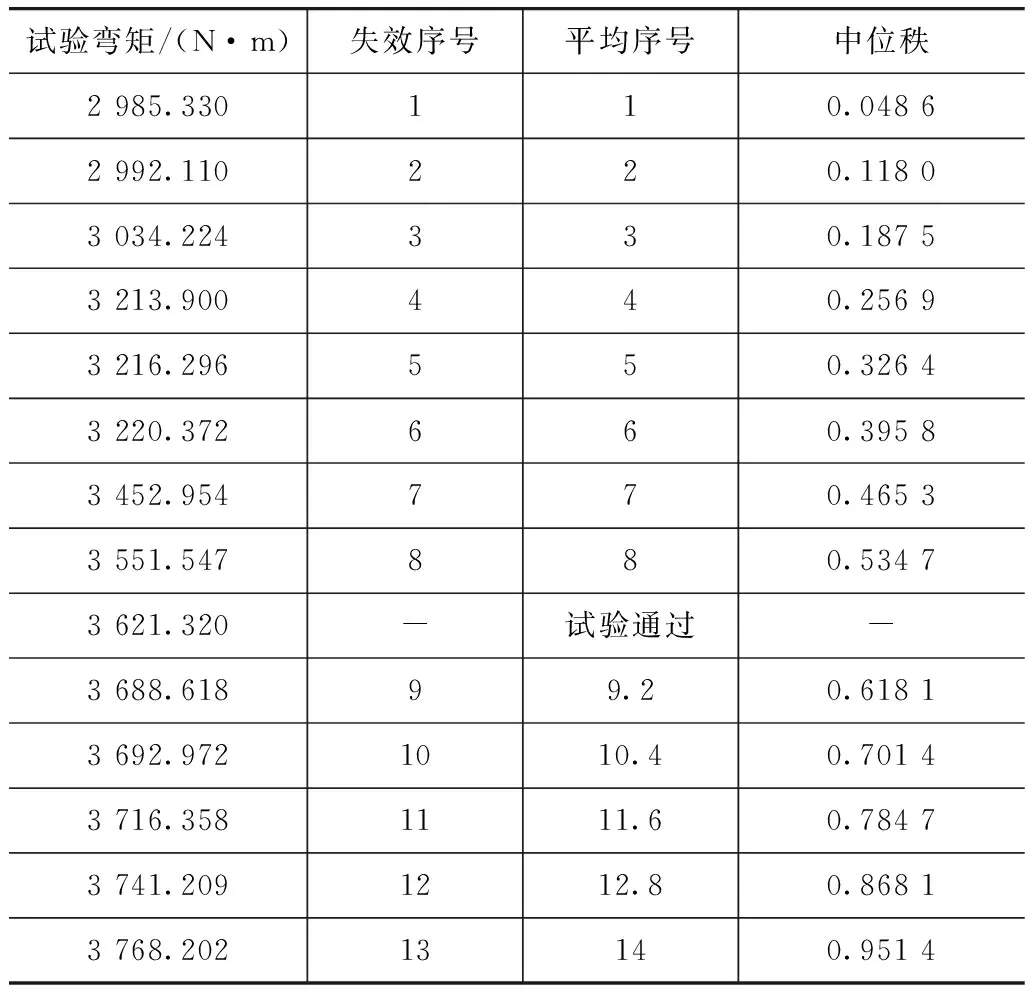
表4 C2曲轴疲劳试验数据
文献[25]中研究了构件疲劳极限载荷的分布规律,提出可以利用正态分布函数统计曲轴的疲劳极限载荷。采用该方法,对C1和C2曲轴的疲劳极限载荷进行分析,可得这两款曲轴的疲劳极限载荷分别为4 290和3 426N·m。
通过对比试验数据与预测结果可以发现,基于KBM多轴疲劳模型预测C1和C2曲轴的疲劳极限载荷,都具有很高的精度,完全满足工程应用的要求;而基于名义应力法预测C1曲轴的疲劳极限载荷时比较准确,但是在预测C2曲轴时的误差较大。
根据文献[9]的分析,在曲轴的主要结构参数中,主轴颈的圆角半径对曲轴的疲劳强度的影响最大。本文中C1曲轴的圆角半径与C0曲轴相等,同为5mm,而C2曲轴的半径为3mm,结构的差异导致预测误差较大。因此对于结构不同的曲轴疲劳极限载荷的预测,采用临界平面法更为精确。
4 结论
(1) 曲轴的弯曲疲劳属于多轴疲劳问题,通过对曲轴在弯矩载荷作用下,应力集中处的应力状态进行分析研究,确定曲轴弯曲疲劳的临界平面和疲劳损伤类型。
(2) 分别采用KBM多轴疲劳模型和名义应力法对同种材料、不同结构的曲轴疲劳极限载荷进行预测,通过对比试验数据发现,传统的名义应力法在预测不同圆角半径的曲轴的疲劳极限载荷时误差较大,而基于KBM的多轴疲劳模型能够准确地预测不同圆角半径的曲轴疲劳极限载荷,具有更为广泛的工程适用性。
[1] 周迅.曲轴疲劳行为及可靠性的理论与试验研究[D].杭州:浙江大学,2006.
[2] TAYLOR D, CARR A J. The crack-modelling technique: optimization of the parameters[J]. Fatigue & Fracture of Engineering Materials & Structues,1999,22(1):41-50.
[3] WANG G, TAYLOR D, BOUQUIN B, et al. Prediction of fatigue failure in a camshaft using the crack modelling method[J]. Engineering Failure Analysis,2000,7(8):189-197.
[4] TAYLOR D, CIEPALOWICZ A J, ROGERS P, et al. Prediction of fatigue failure in a crankshaft using the technique of crack modelling[J]. Fatigue & Fracture of Engineering Materials & Structures,1997,20(1):13-21.
[5] CHEN Xiaoping, YU Xiaoli, HU Rufu, et al. Prediction of crankshaft fatigue limit load by crack-modeling technique[J]. Journal of Advanced Manufacturing Systems,2011,10(1):127-134.
[6] TAYLOR D. Applications of the theory of critical distances in failure analysis[J]. Engineering Failure Analysis 2011,18:543-549.
[7] CLEGG R E, DUAN K, MCLEAD A J. The theory of critical distances and fatigue from notched in aluminium 6061[J]. Fatigue & Fracture of Engineering Materials & Structues,2012,35(1):13-21.
[8] CICERO S, MADRAZO V, CARRASCAL I. Assessment of notched structural components using assessment diagrams and the theory of critical distances[J]. Engineering Fracture Mechanics,2011,78(16):2809- 2825.
[9] CHEN Xiaoping, YU Xiaoli, JI Bingwei. Study of crankshaft strength based on Isight platform and DOE methods[J].2010 International Conference on Measuring Technology and Mechatronics Automation,2010,3:548-551.
[10] 陈晓平,俞小莉,胡如夫,等.采用缺口件等效与渐进插值法预测构件疲劳极限[J].浙江大学学报(工学版),2012,46(3).
[11] 郑康,郝志勇,张焕宇.柴油机机体强度分析与主轴承座疲劳寿命预测[J].汽车工程,2013,35(4).
[12] 陈渊博,郝志勇,张焕宇.基于弯曲疲劳试验的柴油机曲轴疲劳寿命分析及改进[J].内燃机工程,2011,32(1).
[13] FACHERIS G, JANSSENS K G F, FOLETTI S. Multiaxial fatigue behavior of AISI 316L subjected to strain-controlled and ratcheting paths[J]. International Journal of Fatigue,2014,68:195-208.
[14] WALAT K, KUREK M, OGONOWSKI P, et al. The multiaxial random fatigue criteria based on strain and energy damage parameters on the critical plane for the low-cycle range[J]. International Journal of Fatigue,2011,37(4):100-111.
[15] MACHA E, NIESLONY A. Critical plane fatigue life models of materials and structures under multiaxial stationary random loading: The state-of-the-art in Opole Research Centre CESTI and directions of future activities[J]. International Journal of Fatigue,2012,39(3):95-102.
[16] 张莉,程靳,李新刚.基于临界平面法的缺口件疲劳寿命预测方法[J].宇航学报,2007,28(4).
[17] SMITH R N, WATSON P, TOPPER T H. A stress-strain function for the fatigue of metals[J]. Journal of Materials,1970,5(4):767-778.
[18] FATEMI A, SOCIE D F. A critical plane approach to multiaxial fatigue damage including out-of-phase loading[J]. Fatigue and Fracture of Engineering Mateials and Structures,1988,11:149-165.
[19] 张鹏伟.发动机机体疲劳可靠性模拟试验基础问题研究[D].杭州:浙江大学,2012.
[20] 孙楠楠,李国祥,白书战.基于应变—寿命理论的曲轴疲劳分析研究[J].内燃机工程,2014,35(6).
[21] 李文,廖日东,左正兴.高强化柴油机曲轴过渡圆角应力计算的研究[J].汽车工程,2013,35(6).
[22] BROWN M W, MILLER K J. A theory for fatigue failure under multiaxial stress strain conditions[J]. Proceedings of the Institution of Mechanical Engineers,1973,187:745-755.
[23] 周迅,俞小莉.曲轴疲劳裂纹扩展模式的时序方法预测[J].农业机械学报,2007,38(9):163-167.
[24] 周迅,俞小莉.谐振式曲轴弯曲疲劳试验恒载荷控制方法[J].农业机械学报,2006,37(12):168-171,181.
[25] 周迅,俞小莉.曲轴疲劳试验及其数据统计分析方法的研究[J].内燃机工程,2007,28(2):51-55.
A Study on the Equivalent Fatigue of Crankshaft StructureBased on the Theory of Multi-axial Fatigue
Sun Songsong1, Yu Xiaoli1& Li Jianfeng2
1.PowerMachinery&VehicularEngineeringInstitute,ZhejiangUniversity,Hangzhou310027;2.HangzhouBranch,WeichaiPowerCo.,Ltd.,Hangzhou310012
The stress analysis of a crankshaft under bending moment loading is conducted by using finite element method, and the stress states in its stress concentration area are analyzed by applying coordinate transformation scheme to determine the position of critical plane and the fatigue damage types of crankshaft. On this basis, an appropriate multi-axial fatigue damage model is chosen to predict the fatigue limit load of crankshafts with the same material and different structures. The results of comparison between prediction and test show that the traditional nominal stress method has higher accuracy in predicting the fatigue limit load of crankshafts with the same material and same fillet radius, but has relatively apparent error in predicting the fatigue limit load of crankshafts with different fillet radii, while the classical KBM multi-axial fatigue damage model can effectively and accurately predict the fatigue limit load of crankshafts with different fillet radii.
engine crankshaft; multi-axial fatigue damage model; critical plane; fatigue limit load
原稿收到日期为2015年8月28日。

