基于空间几何原理的空间前方交会改进算法

倪晓东

(广东南方数码科技股份有限公司，广东 广州 510665)



基于空间几何原理的空间前方交会改进算法

倪晓东

(广东南方数码科技股份有限公司，广东 广州 510665)

摘要：空间前方交会是摄影测量学重要的概念，通过空间前方交会可以确定待定点的物方空间坐标。在空间几何解析的基础上[1]，根据摄站点、影像点、物方控制点坐标的空间几何关系计算像控点的空间坐标，然后求解待定点的像点空间坐标，从而在物方空间坐标系中进行空间后方交会计算。该方法表达形式直观，便捷实用，并通过实例验证该算法的有效性和正确性。

关键词：空间几何原理；空间前方交会；改进算法

由立体像对左、右2个像片的内、外方位元素和同名像点的影像坐标测量值来确定该点的物方空间坐标，称作立体像对的空间前方交会[2]。文献[3-5]提出使用基于四元素的空间后方交会解算方法，无需依赖初值即可进行空间后方交会解算。为了削弱因线性化产生的模型误差积累，文献[6]专门研究空间后方交会的非线性解算方法。本文根据空间几何原理和影像点与像控点的空间几何关系计算像控点的空间坐标，然后用向量法求解待定点的像点空间坐标，进而在物方空间坐标系中进行空间后方交会计算，与投影点系数法相比，不必计算摄站外方位元素(ω，φ，κ)值，使用空间向量法取代坐标系之间的换算来确定像点的空间坐标，降低计算复杂度，并通过实例验证改进算法的适用性。

1解算原理

立体像对空间前方交会的实质即同名摄影光线对对相交。如图1所示，已知点S1，S2为投影中心，O，A，B为3个地面控制点，o1，a1，b1，o2，a2，b2分别是相应的像点，C为待定点，c1，c2为对应的像点。

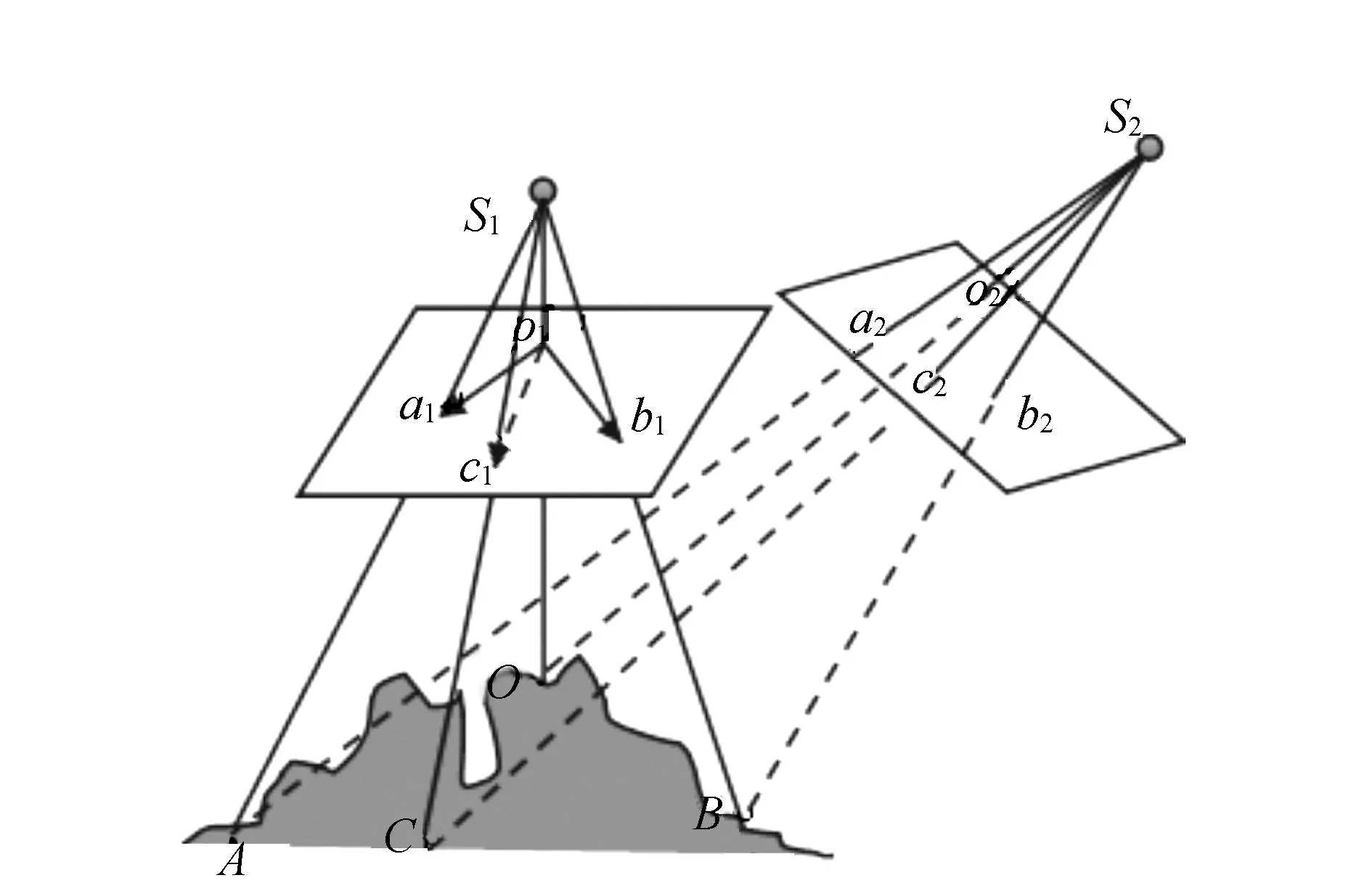
图1　空间后方交会示意图

(1)

由空间几何知识可知，式(1)在空间坐标系中仍成立，从而得到点c1的空间坐标。同理可求出c2的空间坐标，这样就可以建立同名光线Ls1c1，Ls2c2的空间方程式，根据空间直线几何关系求出相交点坐标。由于空间后方交会和像点坐标量测等存在误差，同名光线实际上很难相交，两直线间存在一段距离d。这段距离长度和所在的直线方程均可以求出[1]。如图2，设这段距离所在直线为Ld1d2，分别把直线Ld1d2与Ls1c1，Ls2c2组成两个方程组计算出两个交点d1，d2的坐标。最终交点坐标可以取线段d1d2的中点坐标值。

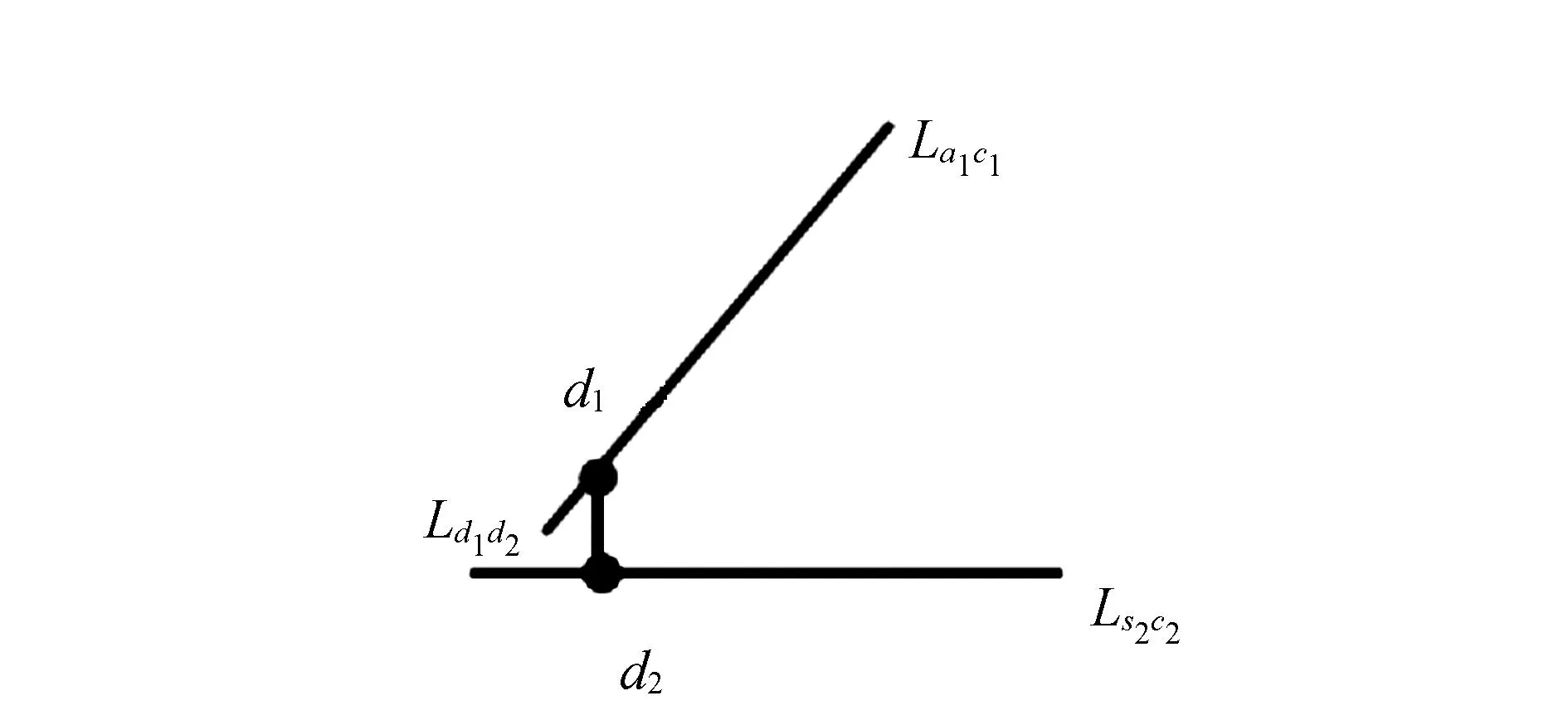
图2　空间直线距离示意图

2像点空间坐标算法

如图3所示，摄影瞬间摄站点、像片和控制点的空间关系为

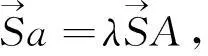
(2)

(3)

(4)

由摄影点S和控制点A的坐标可以计算出像点a的空间坐标。同理，可以根据另外两个控制点计算出像控点b，c的空间坐标(注意控制点不在一条线上)。根据式(1)可得

(5)

式(5)在像平面坐标系和物方空间坐标系中同时成立，且解λ1，λ2相同。这样就可以首先在像平面坐标系中求出待定点像点对应的λ1，λ2。然后由向量关系求出每一个像点对应的物方空间坐标。

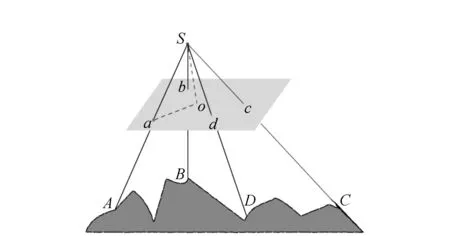
图3　摄影关系示意图

3空间前方交会计算及精度预计

如图1所示，空间内两点确定一条直线。当获得摄影点S1，S2和待定点C对应的同名像点c1，c2的空间坐标，理论上可计算出交会点C的空间坐标。由于误差原因两直线不能相交，如图2，根据空间几何知识可以求出两直线之间距离Ld1d2的空间方程。然后计算出直线Ld1d2与Ls1c1，Ls2c2交点d1，d2的空间坐标值，取线段d1d2的中点坐标为空间前方交会点坐标。

设c1，c2点空间坐标分别为(x1,y1,z1)，(x2,y2,z2)，则距离算式为

(6)

公垂线Ld1d2空间方程算式为

(7)

摄影光线Ls1c1，Ls2c2的空间方程式为

(8)

(9)

分别联立方程式(7)、式(8)和式(7)、式(9)组成方程求解，则得到交点d1，d2坐标，取其平均值为中点坐标，即为空间前方交会结果。

空间几何前方交会计算结果精度取决于空间点坐标值的精度，也就是左右两像片摄影点和像点空间坐标值的精度。根据本文的计算方法，交会点误差等于摄影点误差与相应像点误差之和，即

(10)

式中：m1为摄影点坐标误差；m2为像点坐标误差；k为比例系数。

在数字摄影测量中，像元大小一般在10 μm左右[7]，因此像点坐标量取精度较高。设摄影点与物点坐标距离为1 000 m时，焦距f=50 mm，摄影点误差m1=10 mm，m2=0.001 mm，则M=42 mm，k=d/f。由于结果精度与距离成正比关系，因此该方法可用于近景摄影测量领域。

4算例

通过计算机程序模拟一对立体像对数据，像片1的焦距为55 mm，像片2的焦距为45 mm，内方位元素xo=yo=0，像片1和像片2数据、控制点数据如表1、表2所示。选取a3，b2，b8为像片控点，根据近景摄影测量原理[8]求解摄影点物方空间坐标，进而依据本文算法求出每个像点的空间坐标，然后利用空间前方交会进行计算，结果如表3所示。根据表2、表3数据得出解算结果与实际坐标差值如表4所示。

其中模拟摄影点S1，S2标为(1 075，1 040，20)、(1 070，955，20)，利用角锥法解算摄影点空间坐标结果为(1 075.003，1 039.999，20.001)、(1 069.995，955.992，20.005)。摄影距离在100 m以内。取m1=10 mm，m2=0.005 mm，预计中误差M=±28 mm。

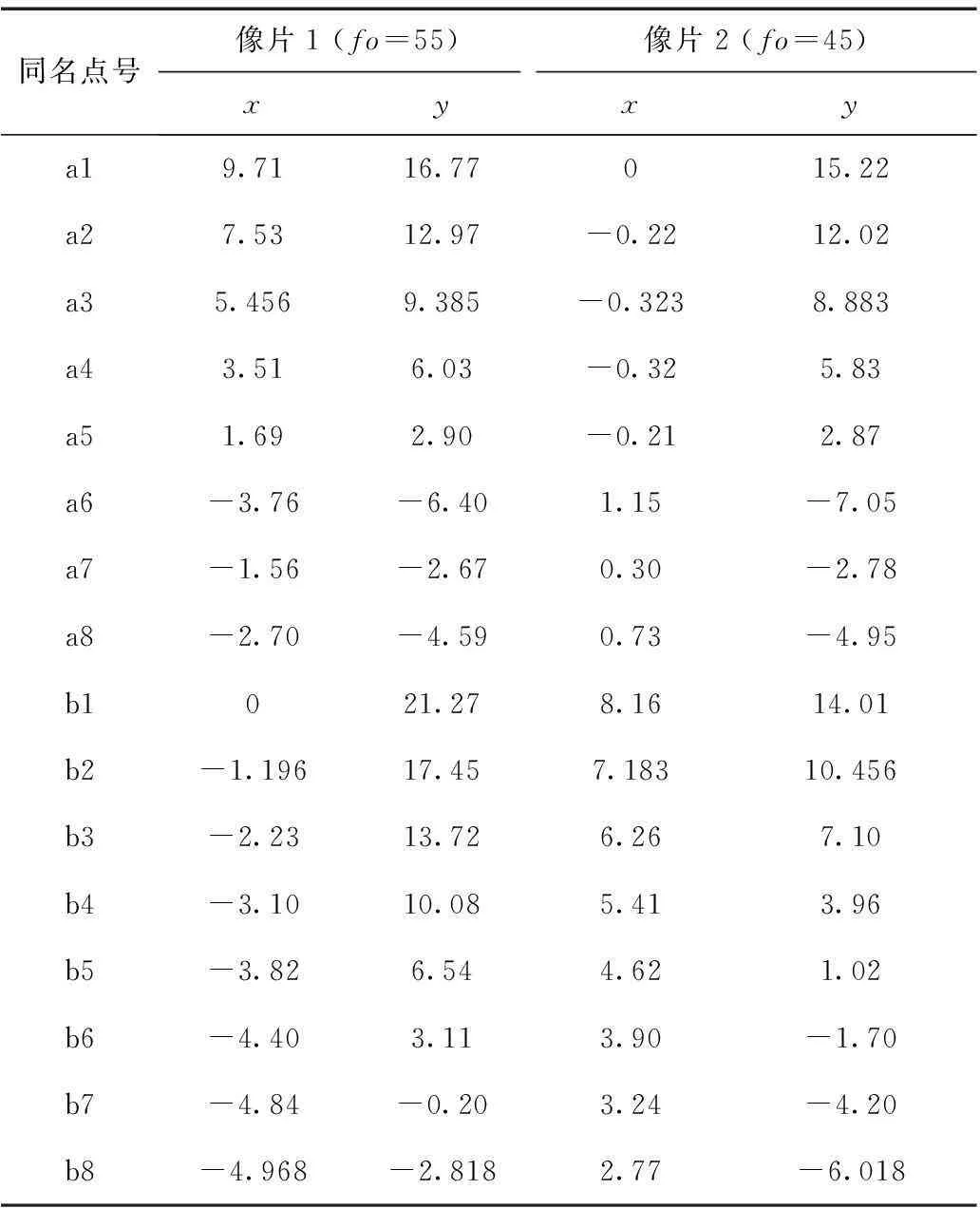
表1　像片1和像片2像点坐标数据　mm

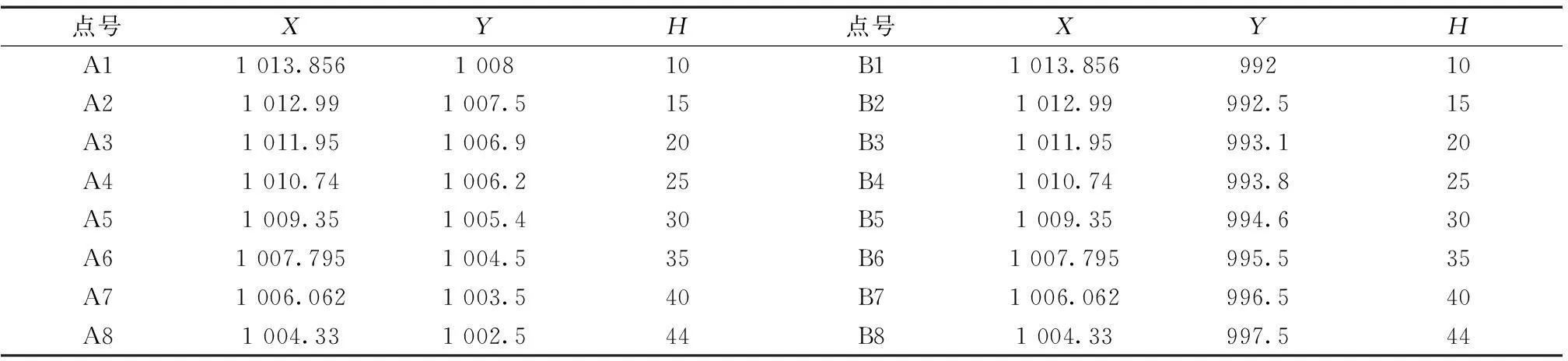
表2　控制点坐标数据　m

表3　控制点坐标解算结果　m

表4　解算结果与实际坐标差值　mm

5结束语

从算例中可以看出，改进后的空间前方交会结果与理论结果相差在2～15 mm，X，Y，H方向的中误差分别为7 mm，3 mm，3 mm，长度中误差为4 mm。利用其他模拟数据验证时发现，计算结果精度主要与摄影基线长度和像点坐标量取精度成正比关系[9]，在合适的基线长度下1 000 m范围内利用此种算法得出的结果基本与理论值一致，从计算过程来看改进后的算法不需要计算相片外方位元素，形式简单，易于解算，可应用到倾斜摄影数据处理[10]，能够根据影像匹配点生成影像特征点云。

本文的空间前方交会计算结果精度依赖空间后方交会[2]计算结果精度和像点坐标测量精度[8]。因此选取多余、分布均匀的控制点和精密量取像点坐标有利于提高空间前方交会计算结果的精度。

参考文献：

[1]谢敬然. 空间解析几何[M]. 北京：高等教育出版社，2013.

[2]官云兰，周世建，周铭，等．基于角锥体原理的空间后方交会改进算法[J]．测绘科学，2006，31(2):27-28.

[3]江刚武,姜挺,王勇,等. 基于单位四元素的无初值依赖空间后方交会[J]. 测绘学报,2011,34(3):181-183.

[4]龚辉,姜挺,江刚武,等. 一种基于四元素的空间后方交会全局收敛算法[J]. 测绘学报,2011,40(5):639-645.

[5]王永波,汪云甲,杨化超. 基于单位四元素描述的单像空间后方交会算法[J]. 中国矿业大学学报,2015,44(3):557-565.

[6]余岸竹,姜挺,江刚武,等. 一种基于非线性最小二乘的空间后方交会算法[J]. 测绘通报,2012(增刊1):199-201.

[7]李军杰，关艳玲，杨蒙蒙，等. 数字航测相机的研究进展[J].测绘科学，2013，38(1):54-56.

[8]冯文灏. 近景摄影测量的基本技术提要[J].测绘科学，2000，25(4):26-29.

[9]张祖勋，杨生春，张剑清，等. 多基线-数字近景摄影测量[J].地理空间信息，2007，5(1):1-4.

[10] 王伟，黄雯雯，镇姣. 倾斜摄影技术及其在3维城市建模中的应用[J]. 测绘与空间地理信息，2011，34(3):181-183.

[责任编辑：张德福]

Modified forward intersection algorithm based on the principle of space geometryNI Xiaodong

(Guangdong South Digital Technique Co.,Ltd,Guangzhou 510665,China)

Abstract：For photogrammetrics, the spatial forward intersection is a very important concept, through which the object spatial coordinates of unknown points can be determined through spatial forward intersection. This paper calculates the spatial coordinates of image control points via the spatial geometric relations of photographic points, the image control points and the control points, based on the geometry of space analytic,solves the image points’ spatial coordinates of unknown points afterwards, and then conducts the calculation of resection in the object spatial coordinate system. At last, this algorithm proves to get the simple expression forms, easy-acceptance and practicability through examples in this paper.

Key words：spatial geometry theory; spatial resection; improved algorithm

中图分类号：P231

文献标识码：A

文章编号：1006-7949(2016)06-0033-04

作者简介：倪晓东(1972-)，男，工程师.

收稿日期：2015-10-10