de Sitter空间中紧致类空超曲面的全脐性与高阶平均曲率

王　琪

（贵阳学院数学与信息科学学院，贵州贵阳550005）



de Sitter空间中紧致类空超曲面的全脐性与高阶平均曲率

王琪

（贵阳学院数学与信息科学学院，贵州贵阳550005）

摘 要：研究de Sitter空间中紧致类空超曲面和高阶平均曲率.利用一个已知的积分公式，得到了关于紧致类空超曲面全脐性的一个新定理.该新定理与已有的一些相关定理不互相包含，从而丰富了大家对全脐性这个几何性质以及高阶平均曲率这个代数不变量的理解.

关键词：de Sitter空间；紧致类空超曲面；高阶平均曲率；全脐性

1977年，Goddard［1］提出猜想：de Sitte空间中有常数平均曲率的紧致类空超曲面必须是全脐的. Montiel［2］给出定理1，证明了Goddard的猜想；李海中和陈维桓［3］研究de Sitter空间中有常数高阶平均曲率的超曲面，在一些附加的条件下证明了定理2；周俊东和宋卫东［4］用活动标架法，给出一个简洁的结果，即定理3.

论文得到定理A，用高阶平均曲率的不同的曲率条件，来刻画de Sitter空间中紧致类空超曲面的全脐性.

定理1［2-3］设Mn是de Sitter空间Sn1＋1中紧致类空超曲面.如果Mn有常数平均曲率，则必是全脐的.

定理2［3］设Mn是de Sitter空间Sn1＋1中紧致类空超曲面.如果有某个整数r （1≤r≤n-1），使得Hr在Mn上为常数，且

在Mn上成立，则Mn必是全脐的.

定理3［4］设Mn是de Sitter空间中紧致类空超曲面.如果Mn有常数标准数量曲率R，且

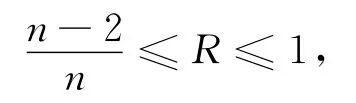
则Mn必是全脐的.

定理A 设Mn是de Sitter空间中紧致类空超曲面.如果存在两个整数r，s，使得

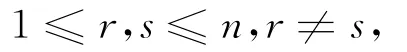
而且Hr在Mn上处处非零，且在Mn上为常数，则Mn必是全脐的.

1　准备和引理

记

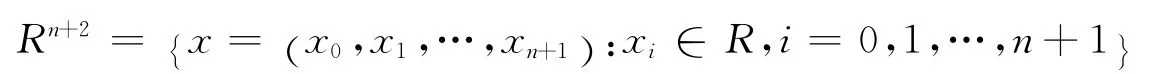
为（n ＋2）维有序实数组全体的集合.

Rn＋2按通常的欧氏度量为欧氏拓扑空间，同时Rn＋2有一个自然的整体坐标系带来的微分结构且是微分流形.

给Rn＋2赋予如下Lorentz度量〈，〉

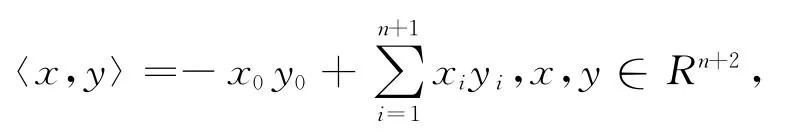
则得一个伪黎曼空间，即（n ＋2）维Lorentz-Minkowski空间［5-9］，记为Ln＋2.

考虑Ln＋2的如下子流形［5-9］

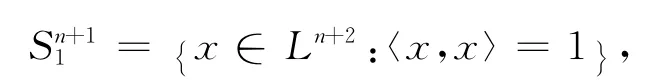
设Mn是的n维浸入子流形.如果的Lorentz度量限制在Mn上时是黎曼度量，则称Mn是的一个类空超曲面［5-9］.

设Mn的主曲率为λi（1≤i≤n），则Mn的第r阶高阶平均曲率Hr定义如下［1-3，5-8］

其中：是通常的组合数.

以下规定

引理1［11-14］如果对某个整数r （1≤r≤n）而言，Hr＞0在Mn上处处成立，则可以选择Mn的适当的光滑法向量场，使得Hk＞0，k＝0，1，…，r-1，r也在Mn上处处成立.

引理2［11-14］对r＝1，2，…，n，有

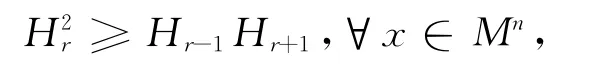
而且对r＝1，2，…，n-1而言，上式当且仅当在Mn的脐点处成立.

引理3［3，6］设Mn是de Sitter空间中紧致类空超曲面，则有

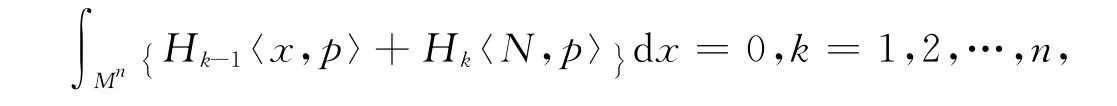
其中：p∈Ln＋2是任意一个固定向量，x∈Mn表示Mn上点在Ln＋2中位置向量，〈·，·〉表示Ln＋2的Lorentz内积，dx是Mn的n维黎曼体积元，N表示Mn上任意选定的一个光滑单位法向量场.

2　定理A的证明

首先，为明确计，不妨设r＞s.

任意选定一个类空向量a∈Ln＋2，则Mn关于a∈Ln＋2的高度函数

该函数在Mn上连续.因为Mn是紧致的，故必有一点x0∈Mn，使得h （x0）达到最大值，而在该点x0∈Mn处，Mn的全部主曲率都非负（适当选定单位法向量场N）.因此，在点x0∈Mn处，有

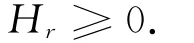
又因为假设Hr在Mn上处处非零而且Hr是连续的，所以，可以适当选择Mn的单位法向量场N，使得

干预组治疗后消化道反应、Ⅲ～Ⅳ度骨髓抑制不良反应发生率明显低于对照组(P<0.05)，差异有统计学意义，见表3。

由上式及引理1，有

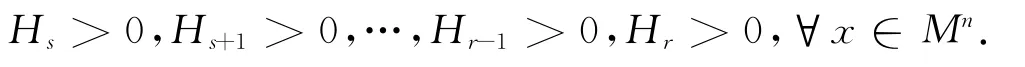
所以，由引理2，有

从引理3的积分公式，有

注意到

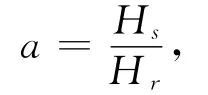
上面积分公式即

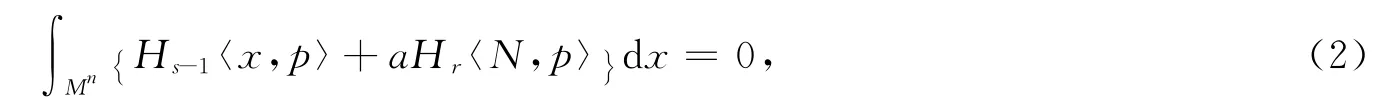
再用引理3的积分公式，得

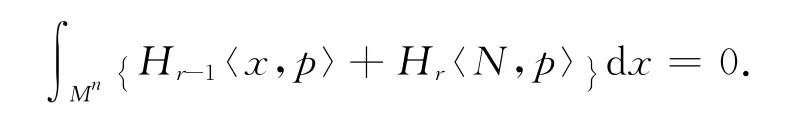
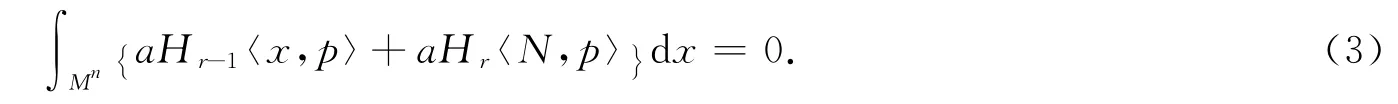
用（3）式减去（2）式，有

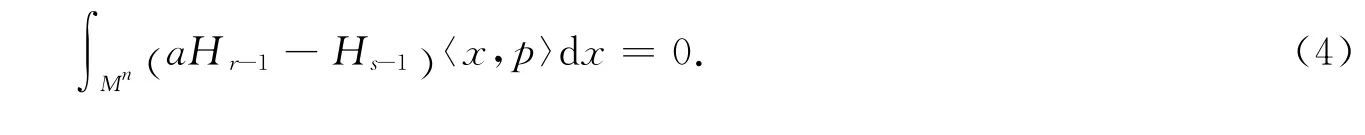
观察（1）式，有

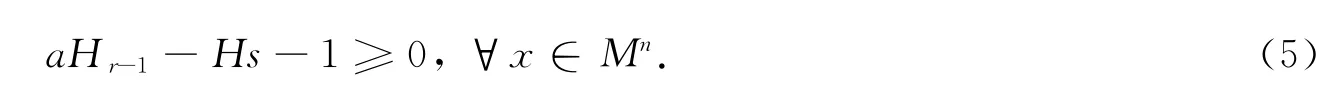
最后，由（4）～（6）式，得到

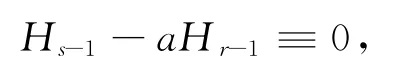
所以，（1）式中的所有不等号事实上都取到了等号.再由引理2，就知道Mn必须是全脐的.

参考文献：

［1］ GODDARD A J.Some remarks on theexistence of space-like hyper-surfaces of constant mean curvature［J］. Math Proc Cambridge Phil Soc，1977，82：480-495.

［2］ MONTIEL S.An inequality for compact space-like hyper-surfaces in de Sitter space and applications to the case of constant meancurvature［J］.Indiana Univ Math J，1988，37：909-917.

［3］ 李海中，陈维桓.de Sitter空间中紧致类空超曲面的积分公式及其Goddard猜想的应用［J］.数学学报，1998，41（4）：807-810.

［4］ 周俊东，宋卫东.关于de Sitter空间中类空子流形的一些刚性定理［J］.纯粹数学与应用数学，2012，28（1）：73-79.

［5］ ALMA L，ALBUJER L J.Spacelike hypersurfaces with constant mean curvature in the steady state space［J］. Proc Amer Math Soc，2009，137（2）：711-721.

［6］ ALEDO J A，Al’as L J，ROMERO A.Integral formulas for compact hypersuffaces in de Sitter space. application to the case of constant higher order mean curvature［J］.J Geom Phys，1999，31：195-208.

［7］ ZHENG Y.Spacelike hypersurfaces with constant scalar curvature in the de Sitter space［J］.Differential Geom Appl，1996，6：51-54.

［8］ ALEDO J A.Curvature property of compact spacelike hypersurfaces in de Sitter space［J］.Differential Geometry and its Applications，2001，14：137-149.

［9］ AKUTAGAWA K.On spacelike hypersurfaces with constant mean curvature in the de Sitter space［J］.Math Z，1996（1）：13-19.

［10］ RRMANATHAN J.Complete spacelike hypersurfaces of constant mean curvature in de Sitter space［J］. Indiana Univ Math J，1987，36（2）：349-359.

［11］ KHO S E.A characterization of round spheres［J］.Proc Amer Math Soc，1998，126（12）：3657-3660.

［12］ BECKEN E F.Inequalities［M］.Berlin：Spring-Verlag，1971.

［13］ MONTIEL S，ROS A.Differential geometry［M］.New York：Longman，1991.

［14］ 王琪.欧氏空间中的全脐超曲面与高阶平均曲率［J］.安徽大学学报（自然科学版），2014，38（5）：7-9.

（责任编辑 朱夜明）

Totally umbilical property of compact space-like hyper-surfaces in de Sitter space and higher order mean curvatures

WANG Qi
（School of Mathematics and Information Science，Guiyang University，Guiyang 550005，China）

Abstract：The totally umbilical property of compact space-like hyper-surfaces in de Sitter space and higher order mean curvatures were studied.By using a known integral formula，a new theorem was attained.Our new theorem was different from some relevant known theorems and thus enriches our understanding of a geometry property i.e.，totally umbilical property and an algebra invariant quantity i.e.，higher order mean curvatures.

Key words：de Sitter space；compact space-like hyper-surface；higher order mean curvature；totally umbilical property

doi：10.3969／j.issn.1000-2162.2016.01.002

作者简介：王 琪（1963-），男，湖南省双峰人，贵阳学院教授，博士.

基金项目：国家自然科学基金资助项目（11561012）；贵州省科技厅科研基金资助项目（黔科合［2014］2005）

收稿日期：2015-04-12

中图分类号：O186.12

文献标志码：A

文章编号：1000-2162（2016）01-0007-04