基于有效检测准则的fMRI源信号数目的估计方法
陈 军,石玉虎,王倪传,曾卫明
(上海海事大学信息工程学院,上海201306)
基于有效检测准则的fMRI源信号数目的估计方法
陈军,石玉虎,王倪传,曾卫明*
(上海海事大学信息工程学院,上海201306)
摘 要:独立成分分析方法已经成功地运用于分析功能磁共振成像数据.尽管独立成分分析方法是一个很有前景的数据驱动分析方法,但是在执行独立成分分析之前,需要确定好独立成分的数目.准确地估计出功能磁共振成像数据中独立成分数目对减少过估计或者低估计能起重要作用,目前有许多信息理论准则方法已经广泛运用于独立成分数目估计中,但通常容易出现过估计现象.该文提出一种基于有效检测准则的fMRI源信号数目的估计方法.模拟数据实验结果表明,该方法对不同平滑数据具有很好的鲁棒性.将该方法用于真实的功能磁共振成像数据中,可以减少色噪声下真实数据的过估计,对功能磁共振成像源信号数目的估计表现出了较好的综合性能.
关键词:功能磁共振成像;独立成分分析;信息理论准则;有效检测准则
功能磁共振成像(functional magnetic resonance imaging,简称fMRI)技术已经成功运用于研究人脑结构及功能活动.目前脑功能连通性检测方法分为:基于模型驱动的方法和基于数据驱动的方法.基于模型驱动的方法往往需要一定的先验知识,而且只能检测与先验知识相关的功能连通网络,很难探测到全脑的功能连通模式;然而基于数据驱动的方法,如经典的独立成分分析(independent component analysis,简称ICA)方法,已经被证实在没有任何先验知识情况下,可以很好地对fMRI数据进行分离[1-2].
独立成分分析的主要目的是解决信号处理中盲源分离问题.在信号处理领域,往往所获得的信号是一些隐藏源信号的线性或者非线性组合;而功能磁共振成像数据实际上是功能磁共振成像时间过程(time course,简称TC)信号,它由不同成分的信号混合构成,其中包括不同任务激活的脑功能信号、头部微小运动造成的伪影信号、机器噪声信号、人的生理脉动信号等.Mckeown等率先把ICA引入fMRI信号的分析和处理领域,并得到了理想的分析结果[1].Calhoun等分别从空间和时间域两个方面,将ICA分为空间ICA[3](spatial ICA,简称sICA)和时间ICA(temporal ICA,简称tICA),其中sICA主要用于分析fMRI数据,而tICA则主要用于分析脑电图(electroencephalograph,简称EEG)和脑磁图(magnetoencephalography,简称MEG)[3-4].
在运行独立成分分析方法前,通常需要确定独立成分的数目,以便对fMRI混合信号进行解混,分解出一个个对应的fMRI源信号成分,使fMRI技术应用在脑功能连通性检测中.如果估计出的源信号数目多于真实源信号数目时,那么将会产生过估计,使得一个源信号分解成两个或者更多的成分[5].相反,如果估计出的源信号数目少于真实源信号数目,那么将会产生低估计,使得各种各样的源信号混合在一起[1,6-8],就丢失了一些重要的信息[8-9],降低了独立信号成分的稳定性,从而很难解释ICA线性分离模型分离出的结果[10],因此准确估计出fMRI源信号的数目是fMRI数据分析的一个重要环节,同时也是事关fMRI技术发挥作用的关键.当前已经有许多信息理论准则方法(information theoretic criteria,简称ITC),如Akaike’s information criterion(AIC)[11],Kullback-Leibler information criterion (KIC)[12],贝叶斯信息理论准则(bayesian information criterions,简称BIC)[13],最小描述长度(minimum description length,简称MDL)[14]等,应用于fMRI源信号数目的估计.通常,这些信息理论准则方法需要满足两个假设条件:一是信号与信号之间满足统计上的独立性;二是信号中所含的噪声为高斯白噪声.然而,由于fMRI混合信号非常复杂,当把这些经典的ITC方法使用在ICA线性模型时,违背了上面提到的两个假设,所以这些经典的信息理论准则方法应用在fMRI数据中,都产生了严重的过估计现象.于是,fMRI源信号数目的估计已经成为当前国内外研究的一个热点和难点问题.由于fMRI数据中体素之间具有相关性,违背了信息理论准则方法的假设条件,于是Li等提出子抽样方法[15],使得样本数据满足独立同分布,符合信息理论准则的假设条件,估计效果得到了明显提高,但是降低了方法的时间效率.Zhao等提出了有效检测准则(the efficient detection criterion,简称EDC)理论[16],证明了该理论具有很强的一致性估计,可以用在加性白噪声模型下进行源信号数目估计.EDC方法在某些情况下,估计出信号数目的收敛速度要快于其他经典的信息理论准则方法[17].后来EDC方法运用在回归问题模型中,相关结果证明其优于AIC,BIC等经典的信息理论准则方法,是一个很好的模型选择方法[18].Gini等将EDC方法应用在雷达信号数目的估计中,并证明了该方法在乘性噪声模型下的估计具有很好的鲁棒性[19].Alkhaldi等将EDC方法运用于眼角膜检测中[20].虽然EDC方法和其他经典的信息理论准则方法有相似的表达形式,但是同其他经典的信息理论准则方法相比,EDC方法的优点在于它的惩罚函数项是可变的,所以针对具体的情况,可以通过调整惩罚项参数使其估计性能达到较好.考虑到fMRI数据的复杂性,使得经典的信息理论准则方法应用于fMRI源信号数目估计产生了过估计的现状,作者拟将EDC方法引入fMRI源信号数目的估计中,通过模拟和真实fMRI数据的实验,来验证该方法在实际应用中的有效性,以及与常规的AIC,BIC,MDL,KIC及最小描述长度抽样法(minimum description leghth subsampling,简称MDLs)[15]相比在效率和估计准确性上的优势.
1 方法
1.1 线性混合模型
x(t,n)代表fMRI数据在时间点为t的第n个体素.一般认为,fMRI数据图像在空间上的一点n是由3维坐标确定的,即n=(nx,ny,nz).在这个线性混合模型中,通常将某个时间点对应的空间点组成一个长向量N=nxnynz.在空间上的线性混合模型[21]表示如下
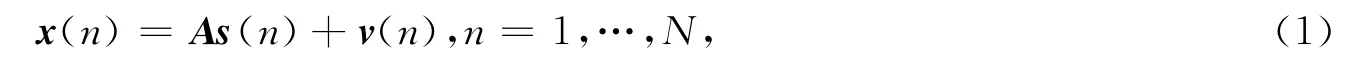
其中:x(n)=[x(1,n),…,x(T,n)]T,A是一个T×M的矩阵(0≤M<T),s(n)=[s(1,n),…,s(M,n)]T是一个源信号向量,v(n)=[v(1,n),…,v(T,n)]是一个零均值、单位方差的高斯白噪声向量,T代表fMRI数据时间点的个数.问题最终就是估计线性混合模型中参数个数M.
1.2 有效检测准则方法
给出N个观测数据x(n)和一系列函数模型族,信息理论准则方法的目的就是选择最适合的模型来拟合这些观测数据.M估计及其相关表达式[22-23]为
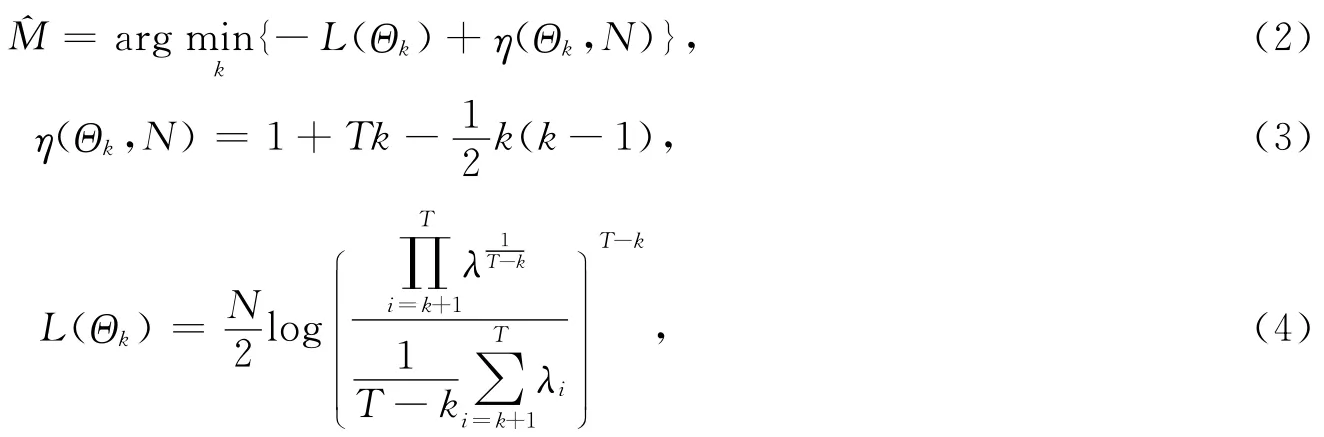
其中:Θk代表模型中所有的自由参数;η(Θk,N)代表惩罚项;L(Θk)是极大似然估计函数;λi是协方差矩阵的第i个最大的特征值.
EDC方法的表达式[20]如下
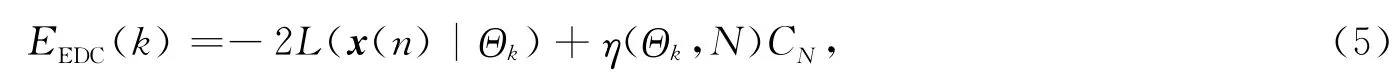
其中:CN必须满足以下条件

EDC方法的惩罚函数项不是固定的,其有下面2种选择形式
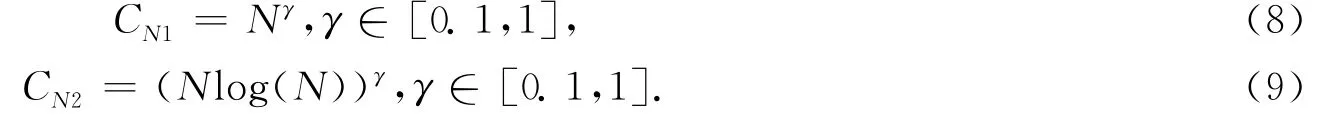
当参数γ被设置很小的时候,容易产生过估计;相反,当参数γ被设置很大的时候容易产生低估计.一般设置参数γ在0.5左右,EDC方法估计性能会比较好.该文EDC方法采用的CN1=Nγ,γ∈[0.1,1],故该文所用的EDC方法表达式如下
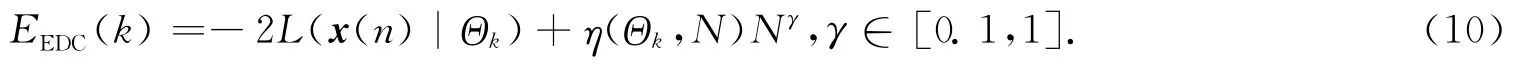
实质上,其他AIC,KIC,BIC,MDL等几种经典的信息理论准则方法和EDC方法的区别在于它们的惩罚函数项不一样,它们的表达式[11-14,23]分别如下
在晨光与夜色的陪伴中,她走遍了镇内12所村级小学,大刀阔斧地进行办学规模的改革,把全镇教师重新组合,做到人尽其才,才尽其用,极大地提高了全镇教师的工作积极性,学校的办学效益和教学质量明显提升。2005年末,小学毕业年级水平测试,数、语、外三科的平均成绩实现了历史性的突破,取得了全县第二名的好成绩。
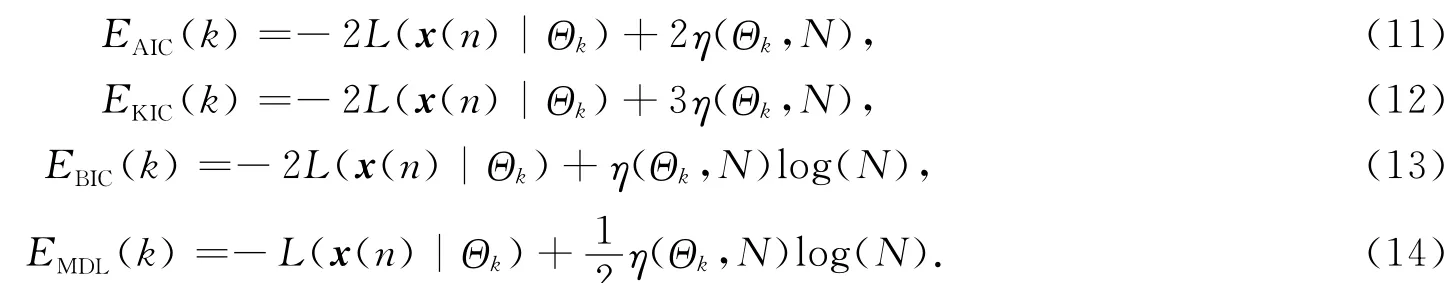
2 数据获取与预处理
2.1 数据获取
2.1.1 模拟数据获取
模拟数据由SimTB软件包[24](http://mialab.mrn.org/software)运行产生.通过SimTB软件的可视化界面来设置模拟被试数据的数目、数据中所含源信号的数目、噪声等.
模拟产生听觉数据,其参数[24]设置如下:模拟被试数据为10个,每个数据中含有27个源信号,体素V=148×148×1,时间点为150个,每个时间点的重复时间(time repetition,简称TR)为2s.设置每个数据中的源信号作一些小的平移、旋转,来模拟数据之间的空间差异性.源信号的空间图序号为ID,除了3个源信号的不在模拟数据中,其他源信号的都在模拟数据中.图1为产生的源信号成分图,其中ID=[27,28]对应的是听觉激活信号,ID=[8]对应的是默认网络下的激活信号,ID=[14,15]对应的是双额下的正激活信号,ID=[4,5]对应的是前额信号,ID=[7]对应的是楔前叶信号,ID=[18]对应的是背侧网络信号,ID=[29,30]对应的是海马区信号,ID=[22,23]对应的是感知运动神经信号,ID=[14,15]对应的是脑脊液信号,ID=[16,17]对应的是白质信号,ID=[6]对应的是内侧额叶皮层信号.定义4种任务事件类型为:1=standards,2=targets,3=novels,4=spike,其中standards代表基准事件,targets代表按钮按下事件,novels代表随机数字噪声产生事件,spike代表尖峰信号事件.所有的源信号在每一个时间过程上的随机事件发生概率为0.2.对于那些不感兴趣的源信号,随机事件的概率幅值设置为1.对于感兴趣的源信号,随机事件以小的幅值(范围从0.2到0.5)添加进去,使得相同事件的相关信号之间相似但又不完全一样.脑脊液信号中含有概率更小的随机事件(概率幅值为0.05).图2为默认基准图像,该图的灰度强度值设置为800.
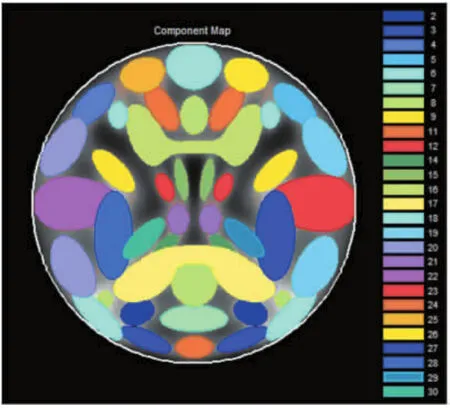
图1 源信号成分图Fig.1 Map of source signal component
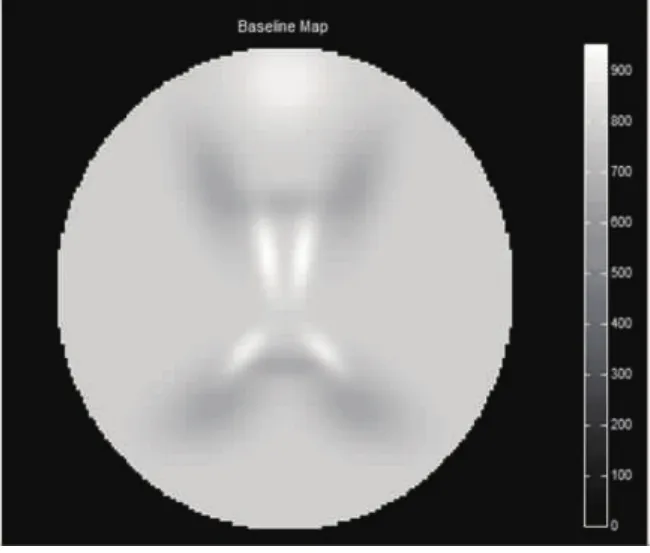
图2 默认基准图像Fig.2 Map of default baseline
2.1.2 真实数据获取
所有数据均通过磁场强度为3T的飞利浦磁共振仪采集,该磁共振仪采用多元素接收线圈,具有并行图像数据采集功能.静息状态数据获取时,被试平躺于磁共振仪内,闭眼保持放松清醒状态,并不做固定性思维.数据通过单次激发敏感梯度平面回波成像获取,图像数为37,敏感加速因子为2.0,TR为2.0,扫描分辨率为80×80,片内分辨率为3mm×3mm,片厚度为3mm,片间隔为1mm.
2.2 数据的预处理
2.2.1 模拟数据的预处理
2.2.2 真实数据的预处理
该文所有计算处理工作均在上海海事大学数字影像与智能计算实验室服务器上进行,其配置如下:intel(R)Xeon(R)E5606 2.13GHz处理器,32GB内存,Windows Server Enterprise Service Pack1操作系统.实验中所有数据的预处理都是采用软件包SPM12进行的.
3 实验结果与分析
3.1 模拟数据实验结果与分析
作者所做的2组模拟数据实验如下:
(1)模拟生成10个被试数据,每个数据中含有27个源信号,对比信噪比(contrast to noise ratio,简称CNR)从小到大分别为0.2,0.4,0.8,1,4,8,10,15,20,30,然后观察比较AIC,KIC,BIC,MDL,EDC 等5种信息理论准则方法在不同CNR下信号数目估计的准确性.
(2)模拟生成一个对比信噪比为1的被试数据,然后使用SPM12对其进行高斯平滑处理,FWHM大小为1~8mm,然后观察比较AIC,KIC,BIC,MDL,EDC等几种信息理论准则方法在不同FWHM下信号数目估计的准确性.
在(1)组实验中,模拟生成10个被试数据,分析比较不同CNR下的各信息理论准则方法估计的准确性,实验结果如图3所示.由图3可知,当CNR很低的时候,如CNR在0.2~0.4之间,各信息理论准则方法都表现出低估计,随着CNR的增大,直到CNR达到8以上时,估计结果接近于真实的源信号数目,所以这些信息理论准则方法在CNR很高的情况下都可以准确地估计出模拟数据中源信号数目.
在(2)组实验中,通过对模拟数据进行高斯平滑处理来提高CNR,分析比较不同FWHM下的各信息理论准则方法估计的准确性,实验结果如图4所示.由图4可知,当FWHM增大到6mm以上时,其他4种信息理论准则方法(AIC、KIC、BIC、MDL)都偏向于过估计,而EDC方法对高斯平滑处理不受影响,具有很好的鲁棒性,估计结果一直很接近源信号数目,所以EDC方法优于其他的经典信息理论准则方法.
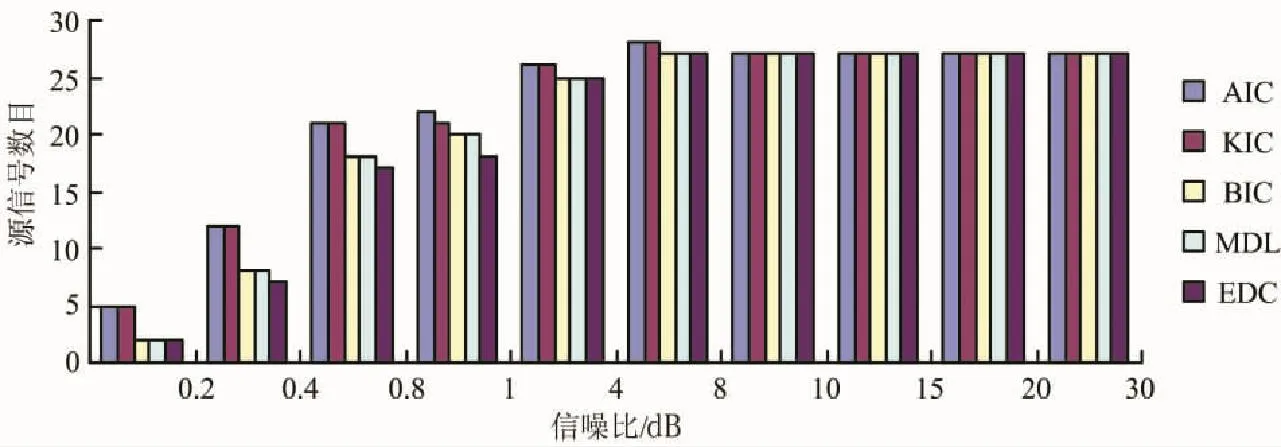
图3 不同CNR下的各信息理论准则方法估计结果的比较Fig.3 Comparison of estimation results using different ITCs with different CNR
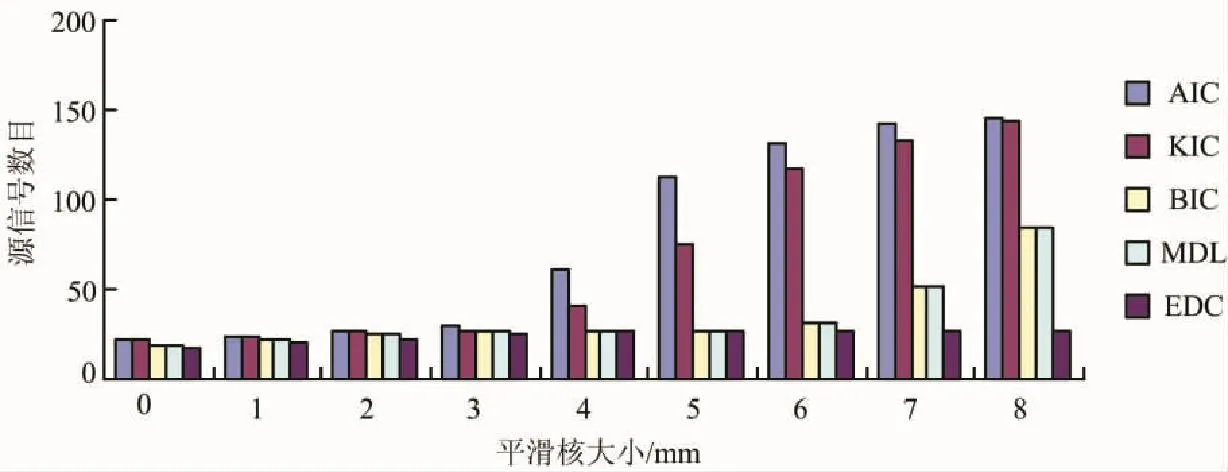
图4 不同FWHM下的各信息理论准则方法估计结果的比较Fig.4 Comparison of estimation results using different ITCs with different FWHM
3.2 真实数据实验结果与分析
作者所做的3组真实数据实验如下:
(1)对于静息状态数据,通过SPM12预处理后得到的数据空间分辨率为91×109×91,时间点为120个,每个时间点的重复时间TR=2s.比较不同的信息理论准则方法的方法准确性.
(2)从方法运行效率方面,分析比较EDC方法和MDLs方法的优劣.
(3)采用ICASSO软件包[25]分析比较各信息理论准则方法所估计出的成分稳定可靠性.
在(1)组实验中,静息状态数据下各信息理论准则方法估计结果如图5所示,由图5可知,当用这些信息理论准则方法估计静息状态数据中源信号数目时,除了MDLs方法和EDC方法不产生过估计现象,其他的信息理论准则方法都出现了过估计现象.
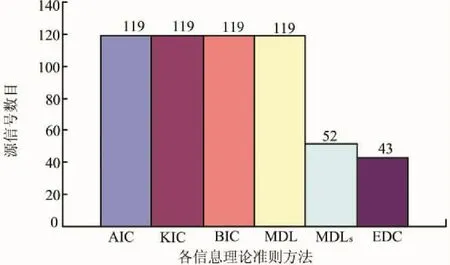
图5 静息状态数据下的各信息论准则方法估计结果的比较Fig.5 Comparison of estimation results using different ITCs with resting state data
在(2)组实验中,选取静息状态数据,然后运行EDC方法和MDLs方法.EDC方法的运行时间为9.832 3s,MDLs方法的为127.627 2s,可见EDC方法的效率明显高于MDLs方法.
在(3)组实验中,对于模拟数据,可以知道其中所含有的源信号数目,这样可以直接评价这些信息理论准则方法估计的性能.然而,对于静息状态数据,却不知道数据中所包含的源信号数目,作者发现可以用ICASSO来分析和评测ICA分离成分的稳定性.
当MDLs方法估计出的源信号数目为52时,通过ICASSO软件包分析与评测,得到聚类质量排序(见图6)和聚类相似2-D图(见图7).从图6可以看出,当聚类的成分标签号在37以后,聚类的质量开始变得很低,说明之后的成分聚类的稳定性很差,不可能是源信号成分,产生了过估计现象.图7中凸包半径小的成分为源信号,半径大的成分不为源信号,而图中出现了很多半径大的成份,不属于源信号,故该图聚类效果不好.

图6 源信号数目为52的聚类质量排序图Fig.6 The cluster quality ranking of the 52sources
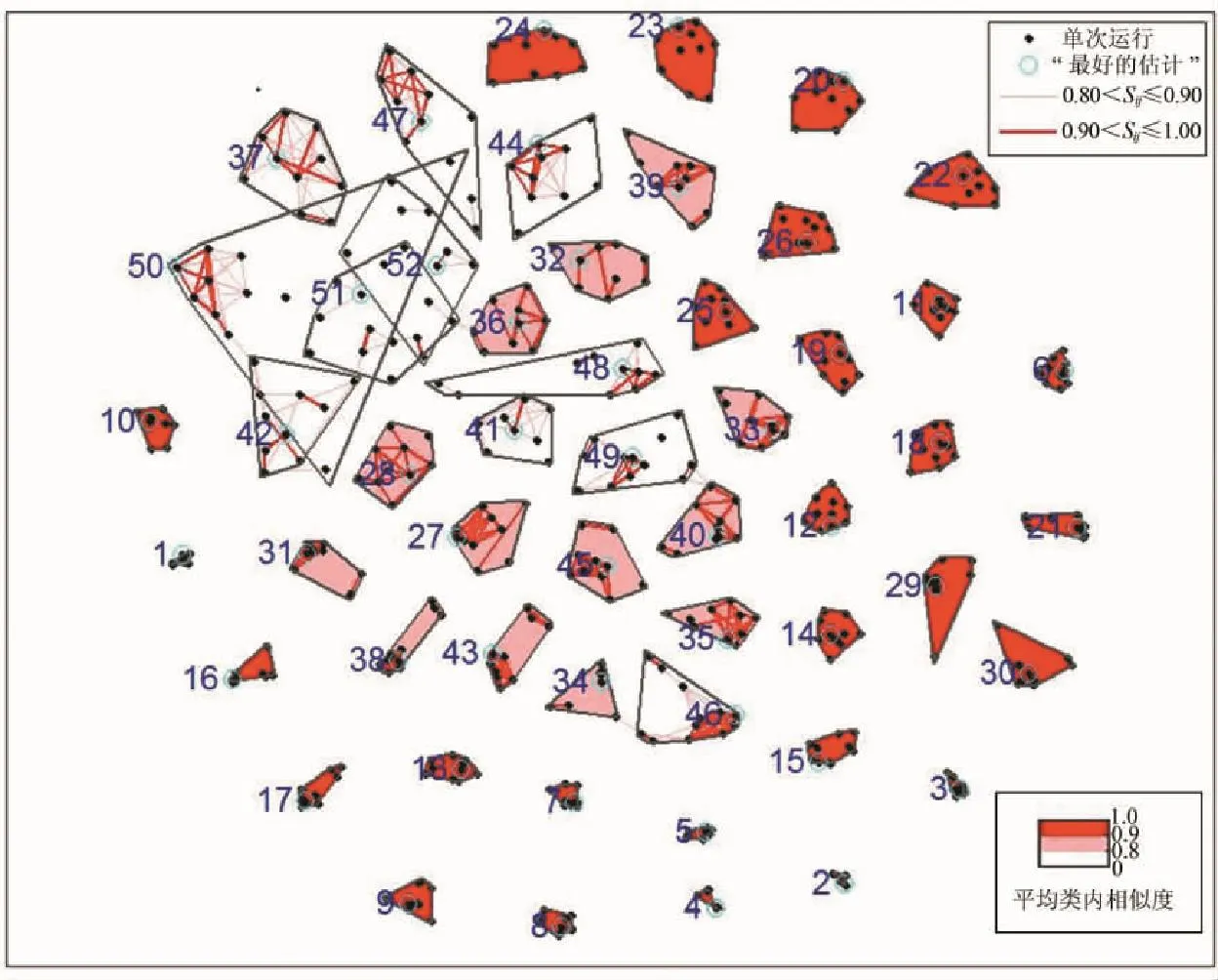
图7 源信号数目为52的聚类相似2-D图Fig.7 Similarity 2-D graph of the 52sources
当EDC方法估计出的源信号数目为43时,通过使用ICASSO软件包来分析与评测,得到聚类质量排序(见图8)和聚类相似2-D图(见图9).从图8可以看出,整体的聚类质量都很高,都大于基本的聚类评测基准0.8.从图9可以看出,整体上聚类的效果很好,凸包的半径都很小,说明成分稳定可靠,估计得很准确.
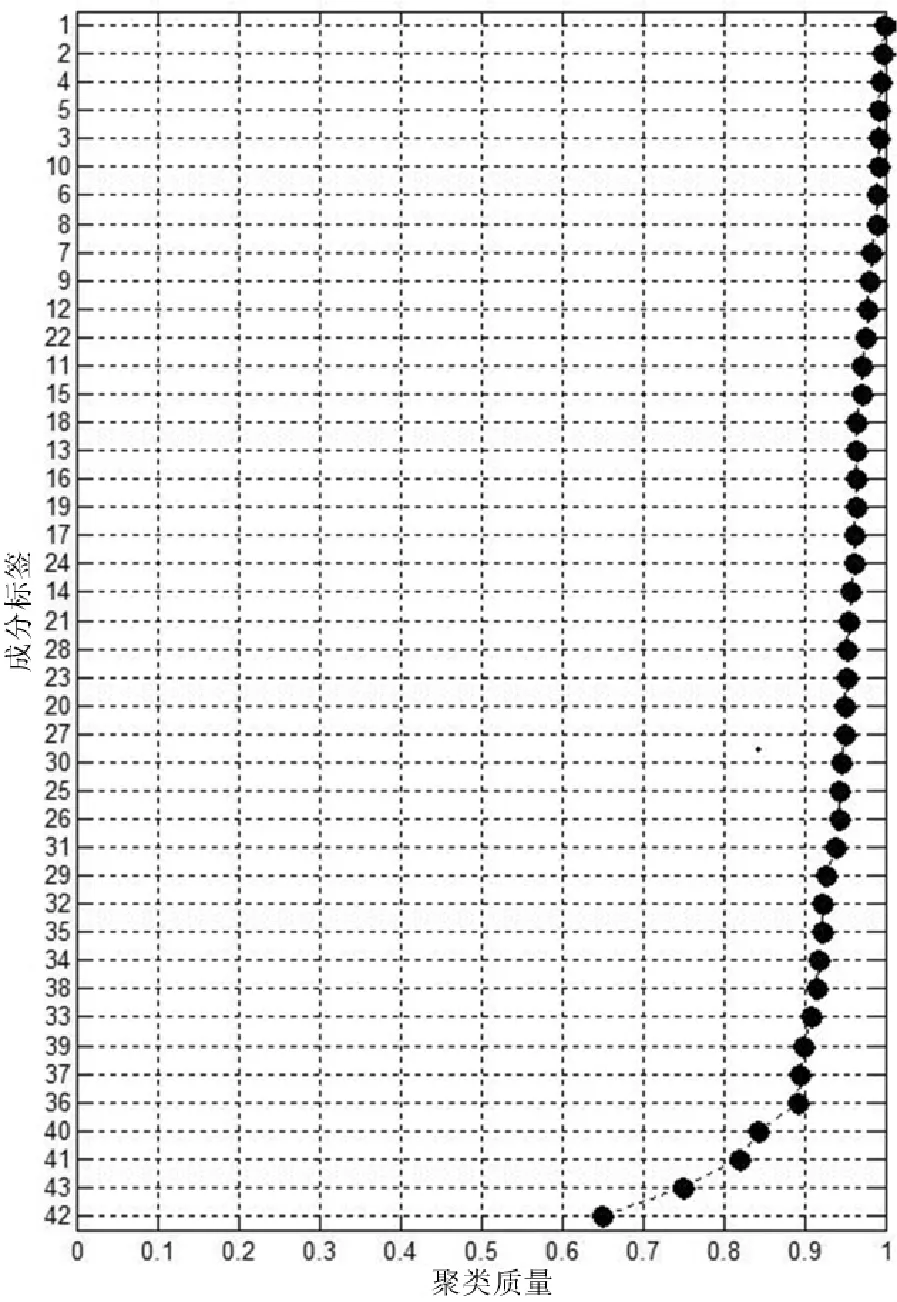
图8 源信号数目为43的聚类质量排序图Fig.8 The cluster quality ranking of the 43sources
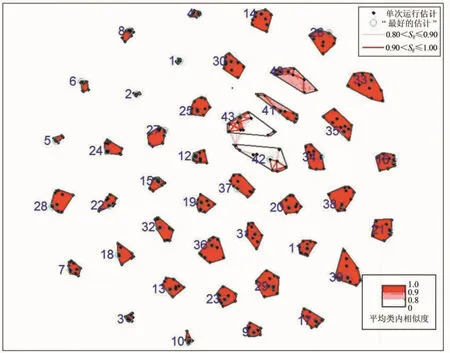
图9 源信号数目为43的聚类相似2-D图Fig.9 Similarity 2-D graph of the 43sources
从上述分析可得出这样的结论:从准确性角度看,EDC方法要好于MDLs方法;从方法的效率角度看,MDLs方法需要对样本数据进行子抽样处理,使样本数据满足独立同分布,而EDC方法可以直接运用于原始数据中,不需要子抽样过程,节省了大量时间.
4 结束语
作者提出了一种使用有效检测准则来估计fMRI源信号数目的方法.实验结果表明,该方法优点如下:(1)该方法可以对色噪声下的fMRI数据源信号数目进行正确的估计,不产生过估计现象,优于其他必须满足高斯白噪声模型下的经典信息理论准则方法.(2)从方法效率以及估计的准确性上,该EDC方法不需要子抽样过程,提高了效率,优于MDLs方法.(3)不同于其他经典信息理论准则方法,该方法的惩罚函数项可变,可以根据具体的问题来调整,使得估计性能更好.
参考文献:
[1] MCKEOWN M J,MAKEIG S,BROWN G G,et al.Analysis of fMRI data by blind separation into independent spatial components[J].Human Brain Mapping,1998,6(3):160-188.
[2] CALHOUN V D,ADALI T K,HANSEN L,et al.ICA of functional MRI data:an overview[C]//In Proceedings of the International Workshop on Independent Component Analysis and Blind Signal Separation,2003:281-288.
[3] CALHOUN V D,ADALI T,PEARLSON G D,et al.Spatial and temporal independent component analysis of functional MRI data containing apair of task-related waveforms[J].Human Brain Mapping,2001,13(1):43-53.
[6] BECKMANN C F,SMITH S M.Probabilistic independent component analysis for functional magnetic resonance imaging[J].IEEE Transactions on Medical Imaging,2004,23(2):137-152.
[7] BARTELS A,ZEKI S.Brain dynamics during natural viewing conditions--a new guide for mapping connectivity in vivo[J].NeuroImage,2005,24(2):339-349.
[8] FORMISANO E,PRVULOVIC D.Functional connectivity as revealed by spatial independent component analysis of fMRI measurements during rest[J].Human Brain Mapping,2004,22(3):165-178.
[9] ESPOSITO F,SEIFRITZ E,FORMISANO E,et al.Real-time independent component analysis of fMRI timeseries[J].NeuroImage,2003,20(4):2209-2224.
[10] MORITZ C H,CAREW J D,MCMILLAN A B,et al.Independent component analysis applied to self-paced functional MR imaging paradigms[J].NeuroImage,2005,25(1):181-192.
[11] AKAIKE H.Information theory and an extension of the maximum likelihood principle[M].New York:Springer,1998:199-213.
[12] CAVANAUGH J E.A large-sample model selection criterion based on Kullback's symmetric divergence[J]. Statistics &Probability Letters,1999,42(4):333-343.
[13] SCHWARZ G.Estimating the dimension of a model[J].The Annals of Statistics,1978,6(2):461-464.
[14] RISSANEN J.Modeling by shortest data description[J].Automatica,1978,14(5):465-471.
[15] LI Y O,ADALT T,CALHOUN V D.Estimating the number of independent components for functional magnetic resonance imaging data[J].Human Brain Mapping,2007,28(11):1251-1266.
[16] HANNAN E J,QUINN B G.The determination of the order of an autoregression[J].Journal of the Royal Statistical Society(Methodological),1979,41(2):190-195.
[17] ZHAO L C,KRISHNAIAH P R,BAI Z D.On detection of the number of signals in presence of white noise [J].Journal of Multivariate Analysis,1986,20(1):1-25.
[18] GINI F,BORDONI F.On the behavior of information theoretic criteria for model order selection of InSAR signals corrupted by multiplicative noise[J].Signal Processing,2003,83(5):1047-1063.
[19] RAO R,WU Y.A strongly consistent procedure for model selection in a regression problem[J].Biometrika,1989,76(2):369-374.
[20] ALKHALDI W,ISKANDER D R,ZOUBIR A M.Model-order selection in Zernike polynomial expansion of corneal surfaces using the efficient detection criterion[J].IEEE Transactions on Biomedical Engineering,2010,57(10):2429-2437.
[21] LI X L,MA S,CALHOUN V D,et al.Order detection for fMRI analysis:Joint estimation of downsampling depth and order by information theoretic criteria[C]//IEEE International Symposium on Biomedical Imaging,From Nano to Macro,2011:1019-1022.
[22] WAX M,KAILATH T.Detection of signals by information theoretic criteria[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1985,33(2):387-392.
[23] HUI M,LI J,WEN X,et al.An empirical comparison of information-theoretic criteria in estimating the number of independent components of fMRI data[J].PLoS ONE,2011,6(12):e29274.
[24] ERHARDT E B,ALLEN E A,WEI Y,et al.Simtb,a simulation toolbox for fMRI data under a model of spatiotemporal separability[J].NeuroImage,2012,59(4):4160-4167.
[25] HIMBERG J,HYVÄRINEN A,ESPOSITO F.Validating the independent components of neuroimaging time series via clustering and visualization[J].NeuroImage,2004,22(3):1214-1222.
(责任编辑 郑小虎)
A new method for estimating the number of sources in fMRI data based on the efficient detection criterion
CHEN Jun,SHI Yuhu,WANG Nizhuan,ZENG Weiming*
(College of Information Engineering,Shanghai Maritime University,Shanghai 201306,China)
Abstract:Independent component analysis(ICA)has been applied to the analysis of functional magnetic resonance imaging(fMRI)data.Although it holds the promise of being a data-driven analysis,we should determine the number of independent components prior to performing ICA.Accurate estimation of the number of independent components in fMRI data is critical to reduce overfitting or underfitting.Several approaches based on information theoretic criteria(ITC)have been implemented in widely used ICA,but they often perform overfitting.In this paper,a new method for estimating the number of sources in fMRI data based on the efficient detection criterion(EDC)was presented.Results of the simulated data showed that the EDC had strong robustness to different smoothed data.Moreover,the EDC was applied to the real fMRI data.Results of the real fMRI data showed that the method could alleviate the overestimation in fMRI data with the colored noise,and the EDC performed better in estimating the number of independent components in fMRI data.
Key words:functional magnetic resonance imaging;independent component analysis;information theoretic criteria;efficient detection criterion
doi:10.3969/j.issn.1000-2162.2016.01.011
作者简介:陈 军(1991-),男,江苏盐城人,上海海事大学硕士研究生;*曾卫明(通信作者),上海海事大学教授,博士生导师,E-mail:zengwm86@sina.com.
基金项目:国家自然科学基金资助项目(31170952,31470954);上海科委基金资助项目(14590501700)
收稿日期:2015-06-30
中图分类号:R319
文献标志码:A
文章编号:1000-2162(2016)01-0064-09

