非方的分数阶退化时滞微分方程的通解形式

张志信，蒋　威

（安徽大学数学科学学院，安徽合肥230601）



非方的分数阶退化时滞微分方程的通解形式

张志信，蒋威

（安徽大学数学科学学院，安徽合肥230601）

摘 要：随着分数阶微分方程在物理、控制等领域的广泛应用，含有退化因素的分数阶微分方程已成为分数阶微分方程理论的研究热点.主要讨论分数阶退化时滞微分方程的系数矩阵在非方矩阵的情况下方程的转化问题和该方程的通解表达式.首先，利用广义逆矩阵理论给出了系数矩阵不是方阵的分数阶退化时滞微分方程的可以正常化的充要条件.其次，利用Laplace变换方法分别给出了非方的分数阶退化微分方程和非方的分数阶退化时滞微分方程的通解形式.所得结果推广了相关文献的相关结果.

关键词：退化微分方程；分数阶；时滞；通解形式

“分数阶微积分”概念的出现至今已有300多年历史，由于没有相关的应用背景，分数阶微积分理论在很长一段时间内都处于理论研究阶段.直至1974年，第一本关于分数阶微分方程的著作《分数阶微积分》［1］出版，同时在美国的New Haven大学召开了首次分数阶微积分会议，分数阶微积分理论迎来了飞速发展时期.最近几十年，分数阶微积分与分数阶微分系统无论是在理论研究还是在具体应用上都有了飞速发展.由于分数阶微分模型可以很好地描述物质的记忆和遗传特性，分数阶微分方程被广泛用来描述光学和热学系统、流变学及材料和力学系统、信号处理和系统识别、控制和机器人等领域［2-7］中的问题.分数阶微分系统可以更好地拟合实际系统，表现出了整数阶微分系统所没有的特性，有很好的应用价值.

由于在控制理论、生物系统、人工智能以及在经济系统中普遍存在退化现象，退化微分系统具有很强的应用价值和理论意义，对经典整数阶退化系统的研究已取得了丰富的理论成果［8-12］.目前，关于分数阶退化微分系统的研究已受到国内外学者的广泛关注.Liu等［13］利用李雅普诺夫方法讨论了分数阶中立型退化时滞微分系统的Mittag-Leffler稳定性条件；Zhang等［14］利用特征值方法研究了线性分数阶退化时滞微分系统的渐进稳定性问题；N’Doye等［15］针对分数阶不确定退化微分方程，利用LMI方法讨论了在Caputo分数阶导数意义下的分数阶退化系统的鲁棒稳定性的充分条件；Jiang等［16］利用Laplace变换研究了分数阶退化时滞微分方程的通解公式，给出了在Caputo导数和Riemann-Liouville导数下系统的解的结果和具体形式；Zhang等［17］讨论了分数阶退化微分方程在Caputo导数意义下的解的表达形式和有限时间稳定性问题.从现有的研究结果看，对于系数矩阵不是方阵的分数阶退化微分方程的研究较少.论文主要讨论系数矩阵不是方阵的分数阶退化时滞微分方程的正常化问题，并在保证方程可以正常化的基础上，利用Laplace变换给出了方程的通解形式.

1　预备知识

定义1［3-4］假设f（x）在［a，＋∞）上是分段连续的，并且在其任何有限子区间上可积，Rep＞0，当t＞a时，则称

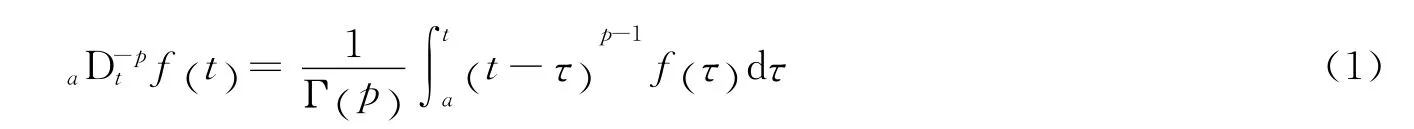
是f（t）的p阶Riemann-liouville分数积分，简称为“R-L分数阶积分”.

定义2［3-4］假设0≤n-1＜α＜n，n∈N，f（t）∈C，并且有n阶连续的整数导数，则

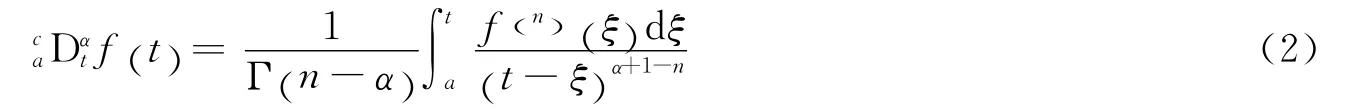
称为f（t）的Caputo分数阶导数.为了区别，在左上角标以c.

注1 当0＜α＜1时，有

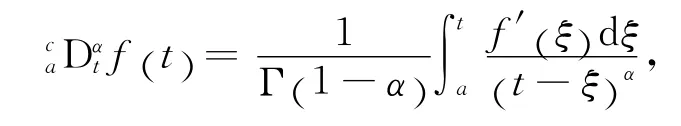
其中

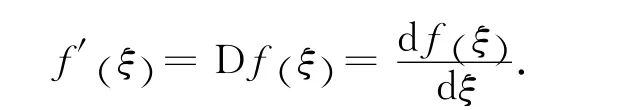
注2 当α→n时，（2）式经过运算右端趋于整数导数f（n）（t），有

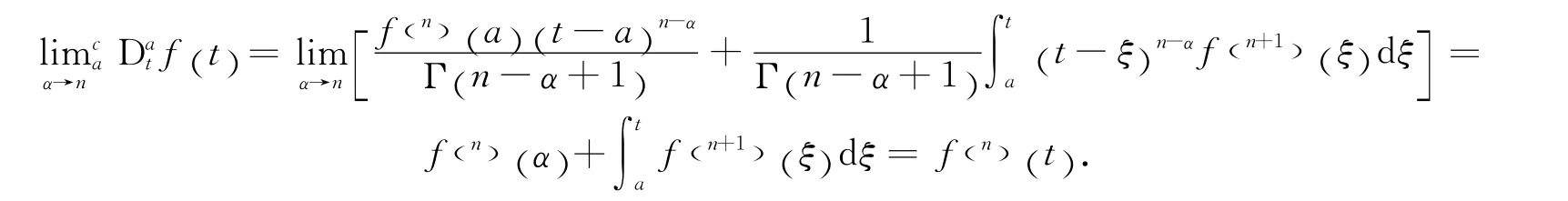
Caputo分数阶导数的Laplace变换定义为

注3 当0＜p＜1时，有

定义3［18］对于矩阵Em×n，若存在矩阵Xn×m满足

EXE＝E，

则称X是矩阵E的半逆矩阵.用E-表示矩阵E的一个半逆矩阵.

注4 E-不是唯一的.

定义4 若微分方程

在一定条件下能转化成和其是同解的正常的微分方程，则称微分方程（3）可以正常化.其中：E∈Rm×n（m≠n）是非方的矩阵，x （t）∈Rn，f （t，x（t））∈Rm，rankE＜n，cDα表示Caputo导数.

2　主要结果

现在考虑非方的分数阶退化微分系统

及非方的分数阶退化时滞微分系统

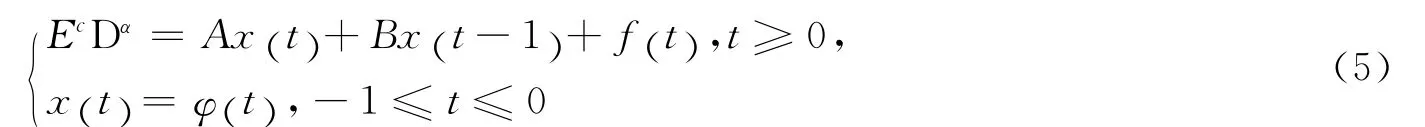
的正常化问题及通解表达式.其中：E，A，B∈Rm×n（m≠n）都是非方的矩阵，x （t）∈Rn，f（t）∈Rm，rankE＜n，φ（t）∈Rn是已知函数，cDα表示Caputo导数，0＜α＜1.

下面讨论系数矩阵不是方阵的分数阶退化微分方程可以正常化的充要条件.

对于系数矩阵不是方阵的分数阶微分方程

其中：E∈Rm×n（m≠n）是非方的矩阵，x （t）∈Rn，f （t，x（t））∈Rm，rankE＜n，cDα表示Caputo导数.

定理1 方程（6）可以被正常化的充分必要条件是存在E-，使得

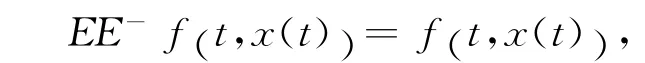
而且方程被正常化以后的表达式为

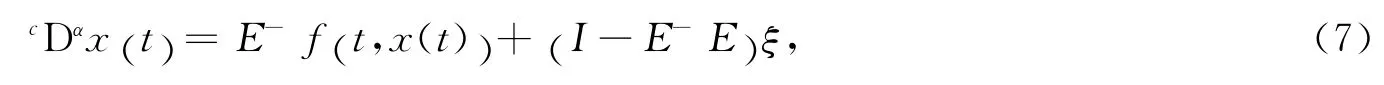
其中：ξ∈Rn是任意向量.

证明 充分性条件.假设存在E-，有EE-f （t，x（t））＝f （t，x（t））式成立，有

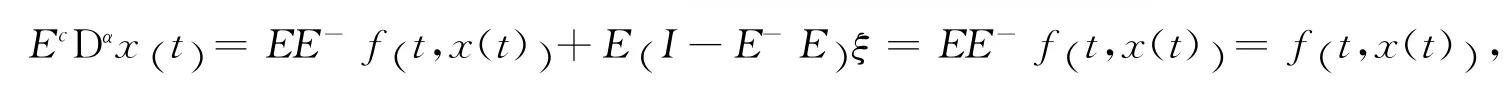
由此可知（7）的任一个解都是（6）的解.

另一方面，对于方程（6）的任意一个解x （t），对x （t）求α阶导数后得到

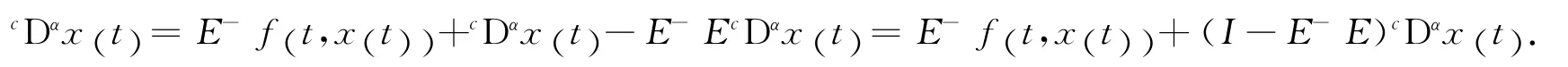
从上式可以看出它具有（7）的形式，即（6）的解是（7）的解.说明（6）和（7）的解是相同的，方程（6）能够正常化.

下面证明必要性.假设方程（6）能够正常化，且具有（7）的形式，则对于任意的E-，有

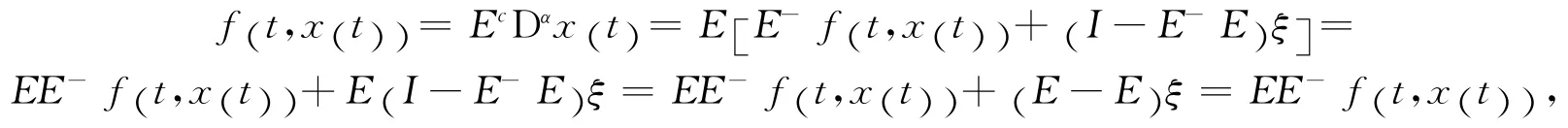
可得条件EE-f （t，x （t））＝f （t，x （t））成立.证毕.

注5 通过一个具体例子来说明条件EE-f （t，x （t））＝f （t，x （t））是有意义的，如

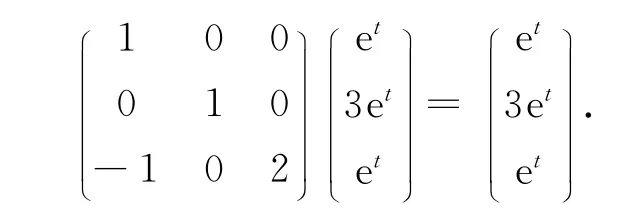
下面在方程（4）满足可以正常化的前提下，讨论该方程的通解表达式.

假设方程（4）可以正常化，那么对其正常化以后方程（4）变成

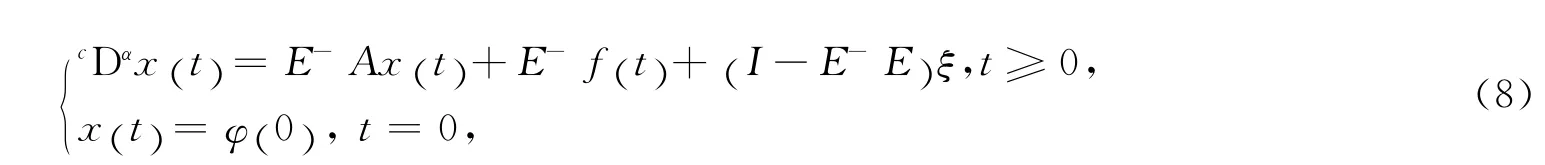
其中：E，A∈Rm×n（m≠n），x （t）∈Rn，f（t）∈Rm，rankE＜n，E-是E的半逆矩阵，ξ是任意向量，cDα表示Caputo导数.

先考虑如下方程

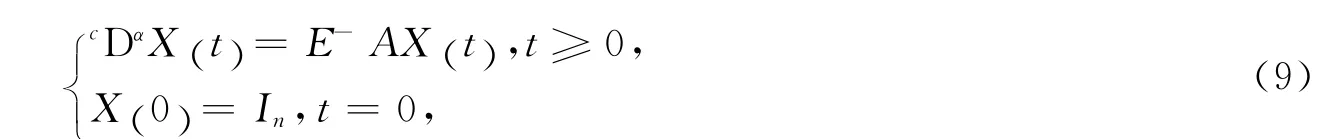
满足方程（9）的解称为方程（8）的基础解.

令H（λ）＝λαI-E-A，由（9）有

其中：L-1是Laplace逆变换.

在得到方程（8）的基础解后讨论方程（8）的通解形式.

对方程（8）两边使用Laplace变换，有

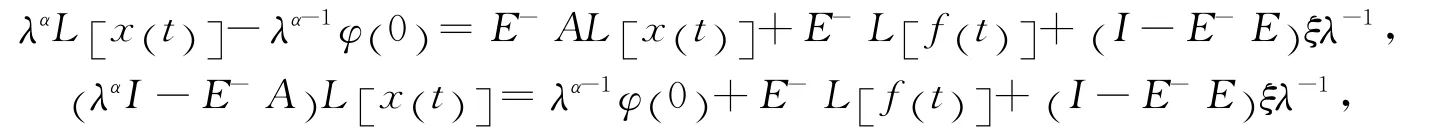
即

又因为，有

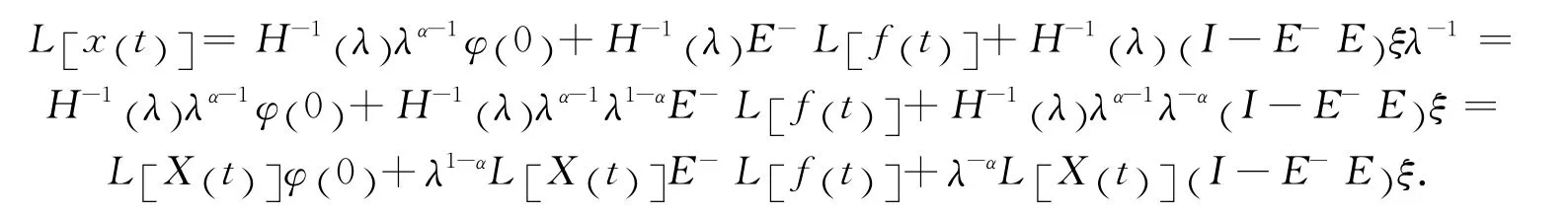
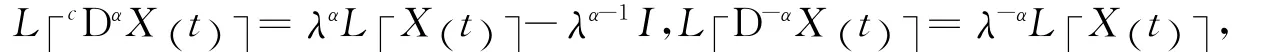
所以，有

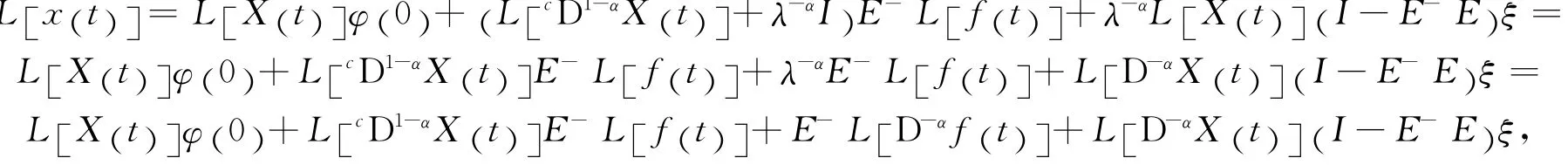
对上式实施反Laplace变换，有

由上面的分析，可以得到下面结论.

定理2 若分数阶退化微分方程（4）可以正常化，那么方程（4）的解的形式为

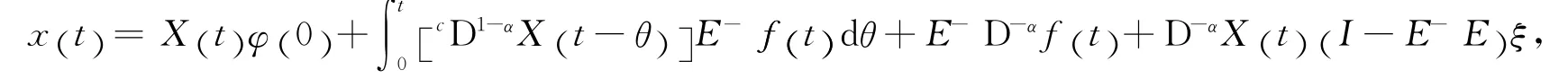
其中：X （t）是方程（9）的解，ξ是任意向量，E-是E的一个半逆矩阵.

下面考虑方程（5）的通解表达式.若方程（5）能够正常化，则正常化以后方程（5）变成

其中：E，A，B∈Rm×n（m≠n）都是非方的矩阵，x （t）∈Rn，f（t）∈Rm，rankE＜n，φ（t）∈Rn是已知函数，E-是E的半逆矩阵，ξ是任意向量，cDα表示Caputo导数.

先考虑如下方程

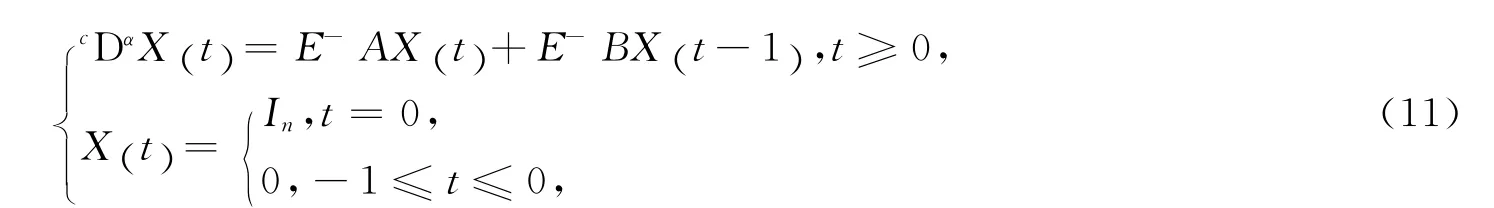
满足方程（11）的解称为方程（10）的基础解.

令H（λ）＝λαI-E-A-e-λE-B，对方程（11）实施Laplace变换可得

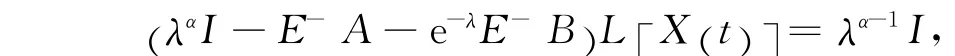
则方程（11）的解为

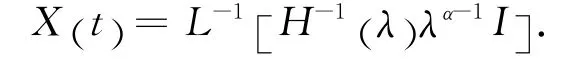
定理3 若分数阶退化时滞微分方程（5）符合正常化条件，那么方程（5）的通解表达式为

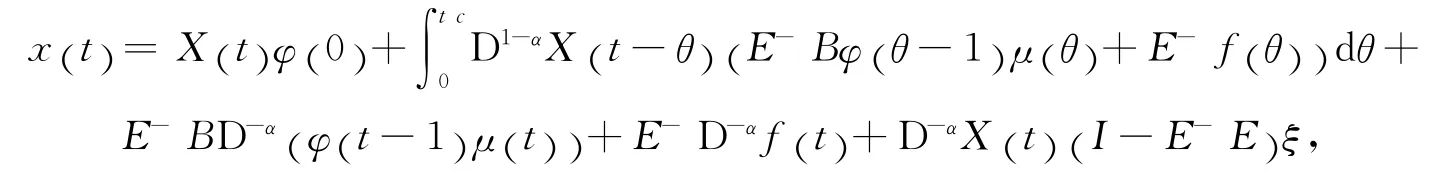
其中

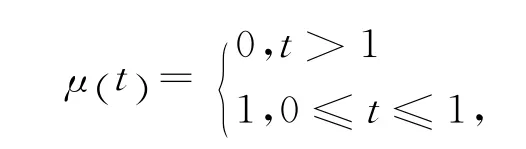
X （t）是方程（11）的解，E-是E的半逆矩阵，ξ是任意向量.

证明 对方程（10）两边同时实施Laplace变换可得

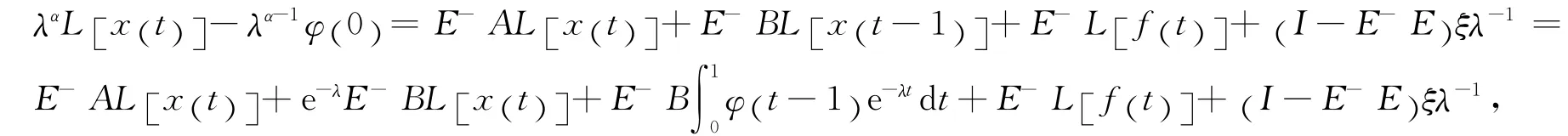
有

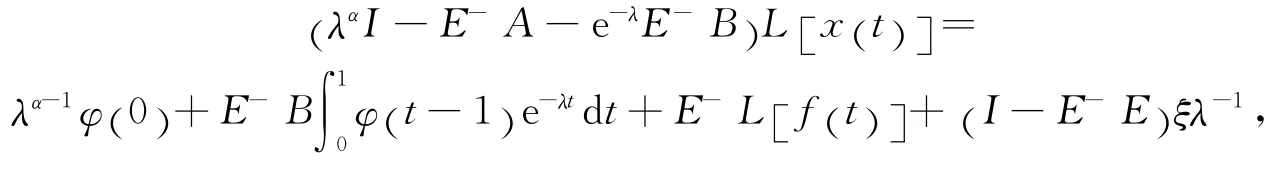
令

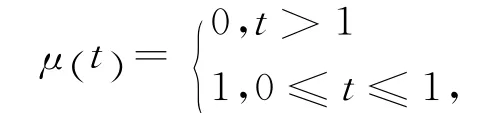
再由

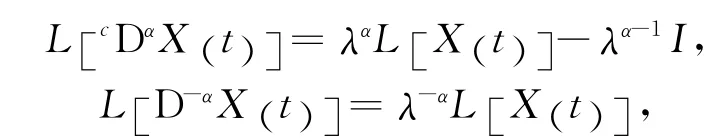
则上式变为

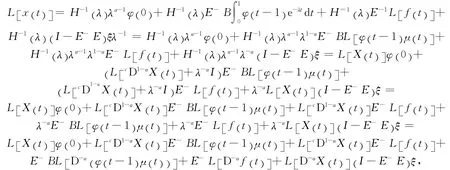
对上式实施反Laplace变换，可得

则（12）式是方程（10）的解，也是方程（5）的解.证毕.

参考文献：

［1］ OLDHAM K B，SPANIER J.The fractional calculus［M］.New York：Academic Press，1974.

［2］ SAMKO S G，KILLBAS A A，MARICHEV O I.Fractional integrals and derivatives theory and applications ［M］.Amsterdam：Gordon and Breach Science Publisher，1993.

［3］ PODLUBNY I.Fractional differential equations［M］.San Diego：Academic Press，1999.

［4］ KILBAS A A，SRIVASTAVA H M，TRUJILLO J J.Theory and applications of fractional differential equations［M］.Amterdam：Elsevier Science B V，2006.

［5］ DAS S.Functional calculus for system identification and controls［M］.Berlin Heidelberg：Springer-Verlag，2008.

［6］ LAKSHMIKANTHAM V，LEEALA S，VASUNDHARA D J.Theory of fractional dynamic systems［M］. Cambridge：Cambridge Academic Publishers，2009.

［7］ DIETHELM V.The analysis of fractional equations［M］.New York：Springer，2010.

［8］ KUNKEL P，MEHRMANN V.Differential algebraic equations［M］.Switzerland：European Mathematical Society，2006.

［9］ DAI L.Singular control systems［M］.Berlin Heidelberg：Springer-Verlag，1989.

［10］ CAMPBELL S L.Singular systems of differential equations［M］.Sanfrancisco London Melbourne：Pitman Advanced Publishing Program，1980.

［11］ CAMPBELL S L，Vu H L.Stability criteria for differential-algebraic equations with multiple delays and their numerical solutions［J］.Applied Mathematics and Computation，2009，208（2）：397-415.

［12］ CHUAN J C，NGUYEN H D，VU H L.On data-dependence of exponential stability and stability radii for liner time varying differential algebraic systems［J］.J Differential Equations，2008，245（8）：2078-2102.

［13］ LIU S，LI X Y，JIANG W，et al.Mittag-Leffler stability of nonlinear fractional neutral singular systems［J］. Commun Nonlinear Sci Numer Simulat，2012，17（10）：3961-3966.

［14］ ZHANG H，WU D Y，CAO J D，et al.Stability analysis for fractional-order linear singular delay differential systems［J］.Discrete Dynamics in Nature and Society，2014，15（6）：172-176.

［15］ N’DOYE I，DAROUACH M，ZASADZINSKI M，et al.Robust stabilization of uncertain descriptor fractional-order systems［J］.Automatica，2013，49（6）：1907-1913.

［16］ JIANG W.The constant variation formulae for singular fraction differential systems with delay［J］. Computers and Mathematics with Applications，2010，59（3）：1184-1190.

［17］ ZHANG Z X，JIANG W.Some results of degenerate fractional differential system with delay［J］.Computers Mathematics with Applications，2011，62（3）：1284-1292.

［18］ 蒋威.退化时滞微分系统［M］.合肥：安徽大学出版社，1998.

（责任编辑 朱夜明）

The explicit representation of solutions for the general fractional degenerate differential equation with delay

ZHANG Zhixin，JIANG Wei
（School of Mathematical Sciences，Anhui University，Hefei 230601，China）

Abstract：With the wide application of fractional differential system theory in the field of physics，control，etc.，fractional degenerate differential equations have become an important topic in the field of the fractional differential equation.In this paper，the transformation problem and the explicit representation of solution were considered for fractional degradation delay differential equations with non-square matrix.By using the generalized inverse matrix theory，sufficient and necessary conditions that guarantee the general fractional degenerate differential equation with delay were normalized.By combining the fractional Laplace transform method，the explicit representation of solution was derived for fractional degenerate（delay）differential equations.The results generalized the corresponding results of the relevant literature.

Key words：degenerate differential equation；fractional order；delay；the explicit representation of solution

doi：10.3969／j.issn.1000-2162.2016.01.001

作者简介：张志信（1976-），男，安徽安庆人，安徽大学副教授，硕士生导师.

基金项目：国家自然科学基金资助项目（11071001，11371027，11201248）；高校博士点专项科研基金资助项目（20123401120001）；安徽省自然科学基金资助项目（1208085MA13）；安徽大学博士科研启动经费资助项目（023033190142）

收稿日期：2015-03-16

中图分类号：O175

文献标志码：A

文章编号：1000-2162（2016）01-0001-06