非标准模型中*-映射的内部刻画

冯晶晶，陈东立

(1.西安培华学院基础部，陕西 西安 710125；

2.西安建筑科技大学理学院，陕西 西安 710055)



非标准模型中*-映射的内部刻画

冯晶晶1，陈东立2

(1.西安培华学院基础部，陕西 西安 710125；

2.西安建筑科技大学理学院，陕西 西安 710055)

[摘要]介绍了超结构的超幂模型及其有关结论，进一步给出了M-映射和e-映射的定义及其性质，得到了*-映射的内部构造以及*-映射的性质.最后用*-映射的内部构造证明了转换原理.

[关键词]超幂模型；M-映射；e-映射；*-映射；转换原理

非标准分析是数学中利用现代数理逻辑，把通常的实数结构扩张为包括无穷小和无穷大的结构后形成的一个分支，是使用非标准模型研究各种数学问题的新的数学理论.非标准分析已被广泛应用到巴拿赫空间、微分方程、概率论、数理经济学、数理物理学等领域.[1-3]关于非标准问题的研究大致分为两个方面：一是对非标准模型的研究；二是利用非标准方法解决标准的数学问题.目前，绝大多数非标准分析方面的文献均是讨论用非标准的方法解决标准的数学问题，提供了把有限数学中的结论和方法应用到无限数学中的可能.[4-7]但已有文献对非标准模型的研究相对较少，随着非标准分析的广泛应用，对非标准模型的深入研究显得尤为迫切.

1预备知识

设S为个体集，令

V0(S)=S，

Vn(S)=Vn-1(S)∪P(Vn-1(S)).

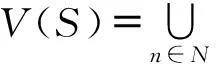
令

V(S)I={f|fδ∈V(S) a.e.，δ∈I}，

即V(S)I为I到V(S)中的全体映射.记

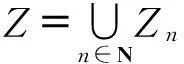
则称Z中的元素为有界映射.定义等价关系f~Fg⟺{δ∈I|fδ=gδ}∈F，容易证明~F是V(S)I中的等价关系.

令

V(S)I/~F={[f]|f∈V(S)I}，

其中[f]={g∈V(S)I|g~Ff}，则称V(S)I/~F为V(S)的超幂，称Z/~F={[f]|f∈Z}为V(S)上的有界超幂.

命题1Z/~F⊆V(S)I/~F.

证明对任意的[f]∈Z/~F，f∈Z，存在某个n∈N使得f∈Zn，从而

fδ∈Vn(S) a.e..

又

Vn(S)⊂V(S)，

所以

fδ∈V(S) a.e.，f∈V(S)I，[f]∈V(S)I/~F.

故

Z/~F⊆V(S)I/~F.

证明

2主要结果

定义1对任意f∈V(S)，设〈f〉为常值映射(f)δ∈I所在的等价类.则称映射e:f→〈f〉为自然嵌入映射.

命题3自然嵌入映射e是V(S)到Z/~F内的单射.

证明任意选取f，g∈V(S)，f≠g，假设e(f)=e(g).由于

e(f)=〈f〉，e(g)=〈g〉，

则fδ=gδ，从而f=g.这与f≠g矛盾，即e(f)≠e(g)，e是V(S)到Z/~F内的单射.

定义2对任意的[f]，[g]∈V(S)I/~F，[f]∈F[g]是指fδ∈gδa.e..

注[f]≠{[g]|[g]∈F[f]}，其中“∈F”与“∈”不同.

设S是个体集，令*S=SI/~F={[f]|fδ∈S}，则*S也是个体集.∀[f]∈*S，存在δ∈I，fδ∈S.由于S为个体集，则fδ≠∅，且对任意的r∈S，r∉fδa.e.，从而[f]≠∅，且对任意的[g]∈*S，[g]∉[f].

类似V(S)的构造，我们构造*S上的超结构V(*S)如下：

V0(*S)=*S，

Vk+1(*S)=Vk(*S)∪P(Vk(*S))，

定理1存在Z/~F到V(*S)内的单射M，使得:

(1) M在*S上是恒等映射；

(2) 对任意的[f]∈Z/~F*S，M([f])={M([g])|[g]∈F[f]}.

证明(1) 定义M为：若[f]=V0(*S)=*S，则

M([f])=[f]∈V0(*S)=*S；

若[f]∈Vn(S)I/~F*S，且已定义了M([f])，则当[f]∈Vn+1(S)I/~F*S时，

M([f])={M([g])|[g]∈F[f]}.

对任意的[f]，[f′]∈Z/~F，且[f]=[f′]，有

M([f])={M([g])|[g]∈F[f]}，

M([f′])={M([g])|[g]∈F[f′]}.

又[f]=[f′]，从而

M([f])={M([g])|[g]∈F[f]}={M([g])|[g]∈F[f′]}=M([f′]).

故M是Z/~F到V(*S)内的映射.特别地，由M的定义知M在*S上是恒等映射.

(2) 对任意的[f]，[g]∈Z/~F，且[f]≠[g]，有

M([f])={M([t])|[t]∈F[f]}，

M([g])={M([t])|[t]∈F[g]}.

若M([f])=M([g])，即

{M([t])|[t]∈F[f]}={M([t])|[t]∈F[g]}，

则

{M([t])|tδ=fδa.e.}={M([t])|tδ=gδa.e.}.

故fδ=gδa.e.，从而f~Fg，[f]=[g].这与[f]≠[g]矛盾，所以

M([f])≠M([g])，

即M是Z/~F到V(*S)内的单射.

定义3令M∘e:V(S)→V(*S).则对任意的a∈V(S)，称*a=M(e(a))为a的非标准扩张.

注对任意的f∈Z，M([f])与*f是不同的.

定理2*-映射是V(S)到V(*S)内的单射.

证明∀x，y∈V(S)，若*x=*y，则M(e(x))=M(e(y)).由于M，e均为单射，所以x=y，即*-映射是V(S)到V(*S)内的单射.

文献[8]指出:一个给定的全域U的形式语言LV(S)由词汇集和公式集两部分组成，如果公式中的变量都不是自由出现的，则称公式为句子.在下面的证明过程中，将有关*-映射分解为M-映射和e-映射的合成.

定理3[9](转换原理)若α为形式语言LV(S)(其中S为非空个体集)中的有界句子，则V(S)|=α，当且仅当V(*S)|=*α.这里的*α是将α中的每个常量u替换为*u而得到的形式语言LV(S)中的句子.

证明对括号的个数m进行归纳证明.

当m=0时， α形如u=v，u∈v，其中u，v是V(*S)中的元.

若u=v，则

*u=M(e(u))=M(〈u〉)=M(〈v〉)=M(e(v))=*v；

反之，若*u=*v，即

M(e(u))=M(e(v)).

由于M，e均是单射，所以u=v.因此u=v，当且仅当*u=*v.

若u∈v，由于

同理可得

M(e(u))∈M(e(v))，

即

*u∈*v；

反之，若*u∈*v，即

M(e(u))∈M(e(v))，

从而

M-1(M(e(u)))∈M-1(M(e(v))).

于是e(u)∈e(v)，同理可得u∈v.所以u∈v当且仅当*u∈*v.由此证得当m=0时定理成立.

假设括号的个数小于m时定理结论成立，则当括号数为m时，α有三种情况：

(ⅱ) α=[β]∨[γ]；

(ⅲ) α=∃xi[δ].

其中β，γ是句子，而δ或是句子或是仅以xi为自由变量的公式.显然β，γ，δ的括号数小于m.下面分情况进行讨论.

(ⅰ) V(*S)|=*α，当且仅当V(*S)|=*β不成立.由归纳假设，V(*S)|=*β不成立，当且仅当V(S)|=β不成立，当且仅当V(S)|=β，即V(S)|=α.所以V(*S)|=*α，当且仅当V(S)|=α.

(ⅱ) V(*S)|=*α，当且仅当V(*S)|=*β，且V(*S)|=*γ.由归纳假设，V(*S)|=*β且V(*S)|=*γ，当且仅当V(S)|=β且V(S)|=γ，当且仅当V(S)|=α.所以V(*S)|=*α，当且仅当V(S)|=α.

(ⅲ) 对V(S)中的任意元素u，用δ(u)表示把在δ中自由出现的xi换成u后得到的公式.若xi在δ中的出现都不是自由的，则δ(u)即是δ.由于xi是δ中可能出现的仅有变量，所以δ(u)中不再有自由变量，故是句子.因δ(u)的括号数小于m，由归纳假设V(S)|=δ(u)，当且仅当V(*S)|=*δ(*u).

若V(*S)|=*α，故存在V(*S)中的元*u，V(*S)|=*δ(*u).由归纳假设V(*S)|=*δ(*u)，当且仅当V(S)|=δ(u)，从而V(S)|=∃xi[δ]，即V(S)|=α.

若V(S)|=α，于是A∈F，当i∈A时，有V(S)中的元素f(i)，使V(S)|=δ[f(i)].设v是V(S)中任一元素，对i∈Ac，令f(i)=v.于是由选择公理，存在f:I→V(S)，使

V(S)|=δ[f(i)].

从而由归纳假设，V(*S)|=*δ[*f(i)]，即存在V(*S)中的元素*f(i)，使得

V(*S)|=*δ[*f(i)]，

即V(*S)|=*α.

综上所述，V(S)|=α，当且仅当V(*S)|=*α.

[参考文献]

[1]LEOB P A. Conversion from nonstandard measure space and application to probability theory [J]. Trans Math Soc，1975，211:113-122.

[2]韩俊峰，韩伟.非标准分析在经济学中的应用[J].西安财经学院学报，2005，18(2):12-15.

[3]ALBEVERIO S，FENSTAD J E，RAPHAEL H K，et al. Nonstandard methods in stochastic analysis and mathematical physics[M]. New York：Academic Press，1990，:362-363.

[4]陈东立，史艳维，董欢欢.向量函数微分的非标准定义[J].东北师大学报(自然科学版)，2015，47(3):37-39.

[5]陈东立，冯晶晶，马春晖.取值于Rd空间上函数积分的非标准定义[J].西北大学学报(自然科学版)，2010，40(3):379-381.

[6]史艳维，陈东立，马春晖.一致可积函数的非标准刻画[J].纯粹数学与应用数学，2008，24(1):82-84.

[7]陈东立，马春晖，史艳维.拓扑的非标准定义[J].西北大学学报(自然科学版)，2006，36(3)：348-350.

[8]李邦河.非标准分析基础[M].上海：科技出版社，1986:25-38.

[9]DAVIS M.Applied nonstandard analysis[M].New York：Wiley，1977:17-28.

(责任编辑：李亚军)

*-Mapping of the nonstandard model

FENG Jing-jing1， CHEN Dong-li2

(1.Department of Basic Courses，Xi’an Peihua University，Xi’an 710125，China；2.School of Science，Xi’an University of Architecture and Technology，Xi’an 710055，China)

Abstract:Firstly，the ultrapowers of the superstructure and some related conclusions are introduced. Then the definitions and properties of the M-mapping and e-mapping are presented. Moreover，the natural construction of *-mapping is given and a property of *-mapping is proved. Finally，the transfer principle is proved by the natural construction of *-mapping.

Keywords:ultrapowers model；M-mapping；e-mapping；*-mapping；transfer principle

[中图分类号]O 141.41[学科代码]110·37

[文献标志码]A

[作者简介]冯晶晶(1984—)，女，硕士，讲师，主要从事应用非标准分析研究；陈东立(1963—)，男，硕士，教授，主要从事应用非标准分析研究.

[基金项目]陕西省自然科学基金资助项目(2007A12)；陕西省教育厅专项科学研究项目(11JK0507).

[收稿日期]2014-08-29

[文章编号]1000-1832(2016)01-0001-04

[DOI]10.16163/j.cnki.22-1123/n.2016.01.001