激光器方舱穿线孔布设位置的EMC预测

葛欣宏，孟范江，宁　飞，贺庚贤

(中国科学院长春光学精密机械与物理研究所，吉林 长春 130033)



激光器方舱穿线孔布设位置的EMC预测

葛欣宏，孟范江，宁飞，贺庚贤

(中国科学院长春光学精密机械与物理研究所，吉林 长春 130033)

[摘要]依据激励电路耦合有限元方法，计算了激光器系统的电磁环境，对激光器方舱穿线孔布设位置进行了EMC预测.首先，在分析了大功率TEA CO2激光器的工作原理基础上，提出了激光器方舱穿线孔布设位置的EMC预测问题；其次，建立了激光器的物理模型，采用激励电路耦合有限元方法，计算了激光器近场区的磁场分布；最后，依据有限元计算的结果，结合场线耦合方法，对激光器方舱穿线孔布设位置进行了分析.结果表明：当激光器处于放电工作状态下，激光器方舱底边的中心处磁场辐射最低(0.79 A/m)，适于布设穿线孔.

[关键词]大功率TEA CO2激光器；有限元法；瞬态磁场；电磁兼容

电磁兼容(EMC)预测是合理进行电磁兼容设计的基础，从设计阶段开始对激光器系统的电磁环境进行定量模拟和估计，能够避免在设备生产完成后，出现电磁不兼容问题导致修改设计甚至重新调整布局.采用系统法进行电磁兼容设计，在元器件已经确定的情况下，空间分离是重要的一步，激光器方舱穿线孔布设位置为典型的空间分离问题，要求在有限的方舱空间内，穿线孔布设位置有限的情况下，设置穿线孔于电磁辐射最弱之处，以使后续的电磁兼容设计能够最优化进行，降低后续电磁兼容设计工作的成本.大功率TEA CO2激光器工作在低频下，近场辐射主要以磁场辐射为主[1]，由于激光器主回路的电流难以测试、计算，且磁场辐射的激励源是周期性非正弦电压源，导致激光器的瞬态磁场分布计算较为复杂，为解决该问题，计算激光器的电磁场辐射是进行线缆布设的先决条件.目前，基本采用将激光器主回路等效为小环天线或偶极子的方法计算激光器的磁场辐射[1-4]，与实际有较大的误差，本文采用电磁场有限元方法可以更精确地对激光器方舱穿线孔的布设位置进行EMC预测.

1EMC预测问题模型

大功率TEA CO2激光器电系统原理如图1所示[5].当触发脉冲Trigger将SG1触发导通时，C1上储存的电量在C1-L1-SG1-C3回路形成脉冲电流I1，C1上的部分电量同时转移至C3；同时，C2经C2-L1-SG1-SG2回路放电，在SG2放电产生的紫外光电离作用下，主电极周围形成等离子区.当C3上的电压上升至主电极之间的气体击穿阈值时，主电极之间的气体被击穿放电，C3和主电极构成回路放电形成脉冲电流I2.依据电磁场理论，电流I1和I2流经的回路为电磁波的辐射源.

激光器方舱空间有限，且工作于放电状态时产生强烈的磁场辐射环境中，方舱内的电磁环境极其恶劣.为降低激光器主机对外的电磁辐射，主体置于屏蔽舱体内(见图2).激光器与电源、控制分系统通过电缆连接[6]，电缆需要穿过屏蔽舱体与激光器主机相连，因此，电缆在屏蔽舱体内的部分会耦合激光器主体的电磁发射，产生电磁骚扰，对控制分系统及供电分系统造成潜在的干扰.系统中电源线传输上万伏高电压，辐射场入射至电源线耦合的骚扰电压相对较小，可以不考虑供电系统的电磁敏感问题，而控制分系统向激光器传送各种开关信号和传感器控制信号，控制电缆在方舱内会耦合电磁场，形成干扰电压与电流传递回控制分系统，一方面，会对控制分系统内的电磁敏感设备造成干扰；另一方面，耦合的干扰信号会导致控制分系统错误动作，因此，需要对电缆进行EMC设计.

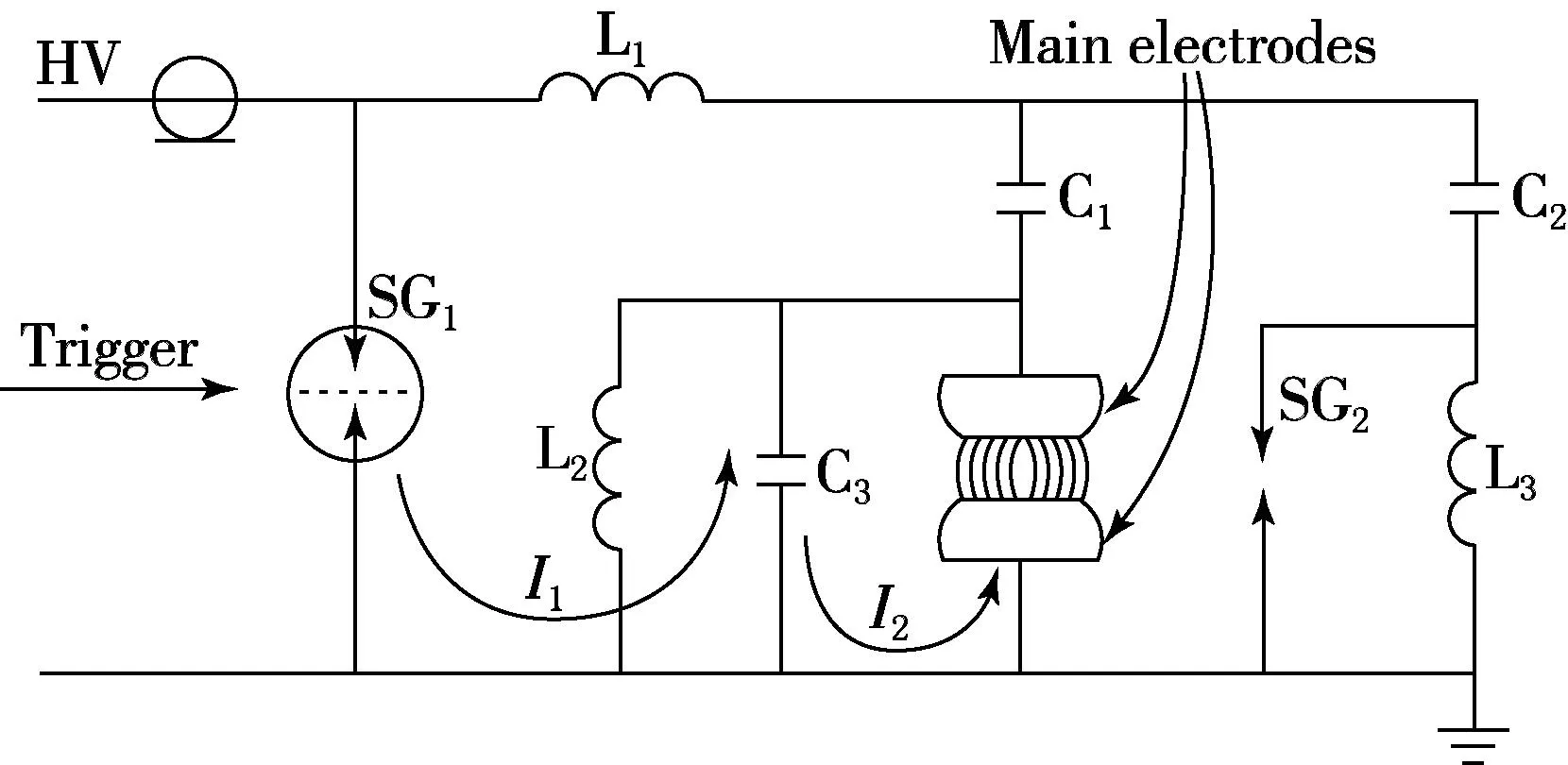
图1　激光器电系统原理图

图2　激光器系统结构

由于屏蔽舱体内各点的磁场辐射强度不同，控制电缆在方舱的不同位置穿入，将耦合不同强度的干扰电压，确定最优的穿线孔布设位置，是电磁兼容设计的重要步骤之一.将穿线孔布设于电磁辐射较弱的空间区域，对后续的电磁兼容设计能起到事半功倍的效果.寻找最优穿线孔布设位置的先决条件是获取屏蔽方舱内的电磁环境分布，由于激光器本身的近场辐射特性为低阻性，近场区性质为磁场，因此，需要对激光器放电状态下的磁场辐射进行计算，并依据计算结果对线上耦合电压进行计算与比较，确定最优的开孔位置.

2激光器瞬态磁场辐射计算

激光器系统在工作状态下，电压上万伏，电流几千安培，且工作频率较低，重频工作于100~500 Hz，电磁场的特性接近于似稳场，因此，可以采用φ-A法进行计算，φ为标量电位，A为矢量电磁位.由于激光器工作在低频段，故位移电流的影响可以忽略.利用φ-A电磁位表示的电磁场方程为：

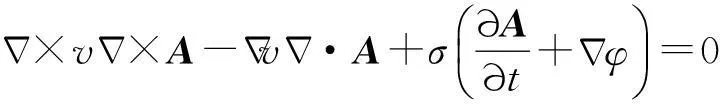
(1)

(2)

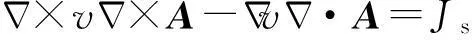
(3)

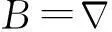
有限元计算的核心思想是将激光器方舱内的整个连续空间用若干个有限单元代替，将微分、积分方程转换成矩阵方程来求解目标值，在ANSOFT MAXWELL中，求解步骤如下[8-10]：

(1) 确定求解区域、边界条件、初始条件——在激光器系统中，求解区域为整个屏蔽方舱的内部，采用金属边界条件，初始条件为默认设置即可；

(2) 划分网格——激光器磁场属于三维瞬态场，因此采用四面体作为基本单元；

(3) 求解——计算出各个节点上的场值；

(4) 后处理——对场进行可视化，并利用求解的结果计算拟布设穿线孔处的磁场强度.

对于带有电压源的实体导体，总电压是已知的，总电流密度是未知的，激励电路计算时采用从实体导体方程导出的电路方程计算未知量.导出的电路方程为：

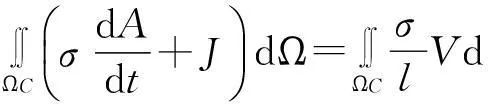
(4)

其中:l为模型的轴向深度，ΩC为导体的横截面宽度，J为待求解的电流密度，V是已知导体电压.

建立激光器的实体结构模型是进行电磁场有限元计算的关键步骤，激光器的实体模型见图3.电路中的电容、电感等器件都封装于火花开关下的金属箱中，器件间通过导电铜带进行电气连接，铜带与电路系统形成闭合回路，回路电流为I1，激光器在工作时，主放电电极上的气体被击穿，形成电流通路，电极与气体放电通道形成闭合回路，回路电流为I2.使I1和I2回路分别等效于实体线圈，实体线圈上的电流分布通过激励电路进行计算，将电路系统与有限元耦合，计算瞬态磁场辐射分布，获得屏蔽方舱内的磁场分布.

图3　激光器实体模型平面示意图

图4　I1回路等效激励电路

图5　激光器放电峰值时刻磁感应强度B的瞬态分布变化图

以I1回路计算为例，I1回路的等效激励电路见图4，其中LWinding为有限元线圈，即电路与有限元耦合分析的接口，由实际测试可得，脉冲电压的上升时间为1.195 ms，火花开关导通、极板可以等效为可变电阻.

将I1回路等效激励电路耦合到激光器的实体模型上，经过计算后，可以得到各个节点上的磁感应强度值B以及B的分布图.激光器放电峰值时刻磁场分布的变化及场值见图5，由有限元后处理结果分析，磁场辐射最强的区域在激光器方舱后半部分，从尽量引入小的耦合干扰和减少电磁泄漏的角度考虑，结合工程设计要求，过线孔只能开在前半部分.

3穿线孔布设于不同位置时EMC预测

开孔区域及位置示意图见图6和7.图6中A区域为可开孔的方舱区域处，区域长为1 m、宽为0.7 m.图7为A区域中拟布置的3个穿线孔，以开孔的圆心坐标来确定位置，3个孔的坐标分别为(0.25，0.55)，(0.5，0.35)，(0.75，0.15).

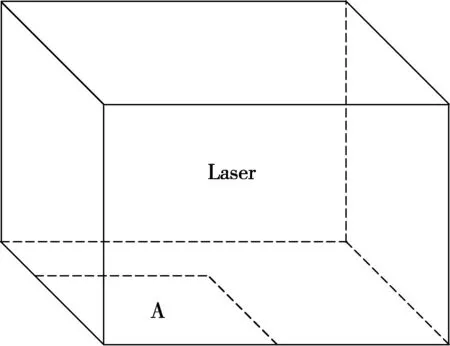
图6　开孔区域示意图

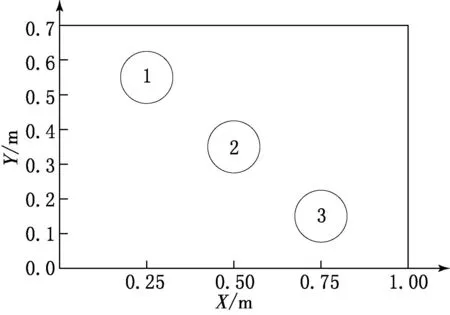
图7　开孔位置示意图

在不同穿线孔处穿入电缆，线缆在屏蔽舱内、舱外的部分及系统地构成一个回路，在回路耦合磁场的情况下会产生耦合电压，耦合电压由

(5)

计算.其中:Zc是空间波阻抗，H为入射的磁场强度，β=2π/λ为传播的相位常数，L为线缆在舱内的长度，h为舱内布线平面距离系统的高度.H可以由

(6)

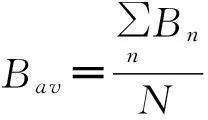
4结论

大功率TEA CO2激光器工作于高电压、非线性状态下，依据激光器的计算电磁学物理模型，采用激励电路耦合有限元方法计算了激光器近场区的电磁辐射分布.计算结果表明，激光器方舱底边的磁场辐射最低，为0.79 A/m，结合工程实际要求，对激光器方舱穿线孔布设位置进行了设计，最终将穿线孔布置于激光器方舱底边的中心处.采用激励电路耦合有限元方法，能够对激光器方舱穿线孔布设位置进行较为精确的EMC预测，同时，该方法对同类型设备的EMC前期设计中的空间分割具有一定的指导作用.

[参考文献]

[1]孟范江，郭立红，杨贵龙，等.大功率TEA CO2激光器系统中电磁干扰的抑制[J].强激光与粒子束，2008，20(2)：177-182

[2]BHATIA M S，KUMAR G. On the EMI potential of various laser types[C].IEEE Proceedings of the International Conference on Electromagnetic Interference and Compatibility，USA：IEEE，2002：3-5.

[3]BHATIA M S，MADAN V K，DONGARE A S，et al. Mapping of radiation field from a discharge laser head[C].IEEE Proceedings of the International Conference on Electromagnetic Interference and Compatibility，USA：IEEE，2002：6-10.

[4]GAYEN A，DAS B N，PODDAR D R. Study of electromagnetic interference from a high power copper vapor laser[C].IEEE Proceedings of the International Conference on Electromagnetic Compatibility，USA：IEEE，2005：847-850.

[5]孟范江，杨贵龙，李殿军.大功率TEA CO2激光系统的电磁兼容设计[J].中国光学与应用光学，2009，2(3):236-241.

[6]孟范江，杨贵龙，李殿军.大功率脉冲TEA CO2激光器控制系统设计[J].激光与红外，2010，40(8)：843-846.

[7]张兴亮，郭立红，张传胜，等. CO2激光器高压脉冲触发系统的设计[J].中国光学，2012，5(4):416-422.

[8]高峰，李守智，张伟，等.基于有限元法的开关变换电路的近场特性分析[J].系统仿真学报，2006，18(7)：1766-1768.

[9]汪泉弟，梁凌红，安宗裕，等.汽车有限元建模及其电磁兼容预测的多软件联合仿真[J].重庆大学学报，2013，36(2)：7-11.

[10]马晓荷，沈颂华.有限元耦合模型在航空电源瞬态特性中的研究[J].系统仿真学报，2009，21(11)：3228-3232.

(责任编辑：石绍庆)

EMC forecast of laser shelter threading hole’s layout position

GE Xin-hong，MENG Fan-jiang，NING Fei，HE Geng-xian

(Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Science，Changchun 130033，China)

Abstract:Based on method of finite element coupled excitation circuit，predicted the EMC for the threading hole layout position of laser shelter. Firstly，based on the analysis of the high power TEA CO2 laser’s working principle，proposed EMC prediction of laser shelter’s threading hole layout position；Secondly，established physical of model lasers，using excitation circuit coupled finite element，Calculated the near magnetic field distribution of the laser；finally，based on the finite element calculation results，combined with field-lines coupling method，analyze threading hole layout position of laser shelter. The results showed that，when lasers working in discharged state，the center of the laser side bilge edge has minimum magnetic radiation. It is 0.79 A/m，suitable for laying threading hole.

Keywords:high power TEA CO2 laser；FEM；transient magnetic field；electromagnetic compatibility

[中图分类号]TN 248[学科代码]510·1025

[文献标志码]A

[作者简介]葛欣宏(1982—)，男，博士，副研究员，主要从事电磁兼容、空间有效载荷电测技术研究.

[基金项目]激光与物质相互作用国家重点实验室研究基金资助项目(SKLLIM0902-01)；吉林省科技发展计划项目(20120331).

[收稿日期]2014-09-28

[文章编号]1000-1832(2016)01-0097-04

[DOI]10.16163/j.cnki.22-1123/n.2016.01.020