如何提高九年级数学复习课的质量

许科文

（福建漳州市龙海程溪中学）

如何提高九年级数学复习课的质量

许科文

（福建漳州市龙海程溪中学）

复习课型是九年级数学教学的主要教与学活动，也是将零散知识系统化，提高学生应试能力的重要课型。但是，如何才能确保复习课的质量最大化呢？随着课程改革的深入实施，教师要通过应用自主学习、合作探究的方式来巩固所学的知识，强化薄弱环节，进而为复习质量的大幅度提高做好保障性工作。

九年级；复习；初中数学；系统化；数学思想；试卷讲评

复习是每节课、每章节、每学期都必不可少的学习形式之一，是学生学习质量的重要影响因素。但是，在应试教育思想的影响下，复习课存在两种现象，一是教师像新知讲解一样，不分重点和难点的全部讲解，导致复习计划不能按时完成。二是做练习，学生每天做好几张卷子，整个复习就是让学生做练习，教师讲试卷的过程，学困生的基础知识也没有巩固等等。事实上，这两种复习方式都是不利于复习质量的提高的，也是不利于课堂全面发展的。所以，为了充分发挥复习课的作用，也为了提高学生知识的灵活应用能力，在复习时，我们认真贯彻落实“以生为本”的教学理念，要鼓励学生在自主复习、小组交流中将零散知识系统化。因此，本文就从以下几个方面入手对如何提高九年级数学的复习质量进行论述，以期能够提高学生的复习质量。

一、系统零散知识，明了复习方向

有效地将零散知识系统化是复习教学的主要目的之一，但是，在以往的复习过程中，为了节省时间，我们教师采取的都是教师整理，学生抄写、背诵的活动，学生不参与整理，也不参与找寻知识与知识间的异同，事实上，这种方式虽然能将知识系统化，但并不利于学生复习效率的提高。所以，在落实“以生为本”的数学复习课堂中，教师要鼓励学生结合教材，结合自己的理解对零散知识进行整理，一来能够加深学生的印象，二来能够帮助学生找到知识与知识之间的关系，促使学生在考试中能够灵活地应用知识。

例如：找相近的知识，并进行整理。如：将“平行四边形的判定”“正方形的判定”“矩形的判定”“菱形的判定”“等腰梯形的判定”这几部分的知识进行整理，自主对“性质”“判定定理”两方面进行整理，并找出判定定理之间的关系。比如：

平行四边形判定定理：对角线互相平分的四边形是平行四边形。

矩形的判定定理：对角线相等的平行四边形是矩形。

将这两个定理进行结合，可以归纳为：对角线互相平分且相等的四边形是矩形。

菱形的判定定理：对角线互相垂直的平行四边形是菱形。

再次将平行四边形与菱形的判定结合在一起，可以归纳为：对角线互相平分且互相垂直的四边形是菱形。

……

在这样的系统整理下，不仅将零散的知识系统化，锻炼学生的知识应用能力，而且对学生解题思路的形成，对学生解题能力的提高也有着密切的联系。当然，除了这一方法外，我们可以组织学生制作思维导图，以某章节为单元来制作，将相关的知识点比较完整地展现出来，进而使学生在自主整理中提高复习质量。

二、渗透数学思想，提高复习效率

掌握数学思想就是掌握了数学的精髓，在复习中渗透数学思想不仅能够让学生掌握知识的本质，培养学生的创新能力，而且对学生思维能力的提高和解题能力的锻炼都有着密切的联系。所以，在九年数学复习的过程中，教师要有效地渗透数学思想，进而使学生在思想的指导下提高学习效率，同时，也能大幅度提高学生的考试能力。

例如：以换元法为例，这种方法在初中代数中也是常用的，比如：

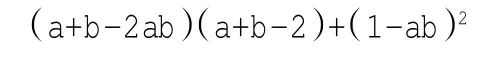
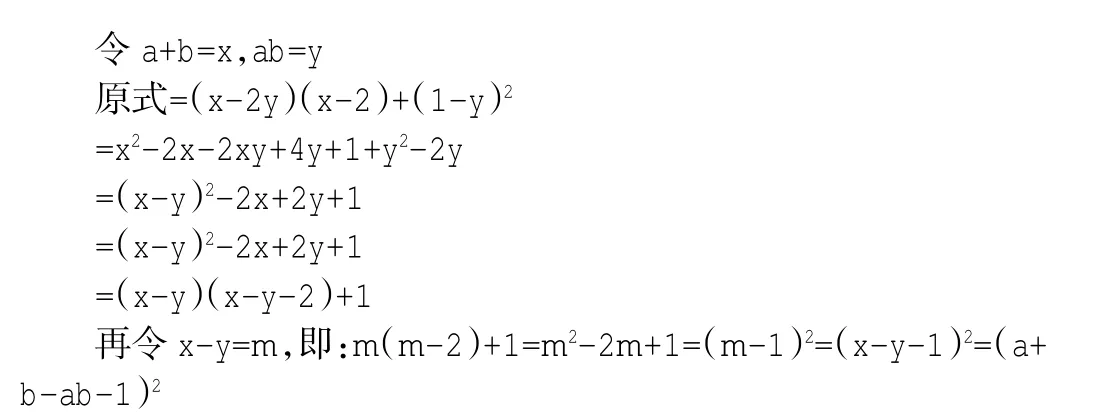
这道题是换元法的有效练习题，是两阶的换元，也是渗透化归转化思想的主要类型的练习题。但是，在以往不论是授课还是复习，我们常常强调的都是换元，导致很多学生一直在纠结应该替换哪些，替换之后是否简单等，这是不利于学生解题效率的提高的。所以，在复习时，我们不仅要明确换元法，还要明确地渗透化归、转化思想，进而使学生在数学思想的指导下锻炼数学学习能力，进而能确保高效课堂的顺利实现。

三、小组互相讲评，锻炼复习能力

试卷讲评是复习的重要环节，是明确学生改进方向，了解自己薄弱环节的主要内容，也是影响复习质量的重要方面。所以，在复习中的试卷讲评环节，我们可以借助小组合作讲评活动来打破传统的教师一讲到底的模式，并确保学生在互相学习、互相帮助突破难点的过程中掌握知识，提高复习效率。

首先，按照学生的学习情况，以同组异质的原则将学生分成不同的小组，目的就是要实现优等生带动学困生的效果。所以，对于复习讲评中的一些基础性试题，比如：关于x的一元二次方程x2-2ax+3a=0的两个相等的实数根，则a的值是________等难度系数较低的题目，则由小组内的优等生来进行讲解，这样也能实现一对一的效果。而对于一些中等难度的练习题，如：在△ABC中，AB=AC，D是BC上一点，DE⊥AB，DF⊥AC，垂足分别为E、F，且E、F分别是AB和AC上的点，且DE=DF，图略，请选择一对你认为全等的三角形并加以证明。

（1）你选择的是：△_______≌△_______

（2）证明：______________

这是一道开放性练习题，首先，组织学生根据题意进行画图，然后，自主提出可能是全等的两个三角形，并自主进行证明。随后，在与小组成员进行交流，这样不仅能够发散学生的思维，拓展学生的知识视野，而且对学生解题能力的提高也有着密切的联系，当然，也有助于讲评能力的提高。

综上可见，有效的复习活动不仅能够将零散的知识系统化，提高学生的学习能力，而且也能在巩固已经掌握知识的基础上使综合知识应用能力得到大幅度提高，进而也为学生的发展做出相应的贡献。

［1］黄结辉.浅谈如何提高初三数学复习课的质量和效率［J］.中学课程辅导（教师教育），2016（8）.

［2］曹艳华.九年级数学复习课的有效做法［J］.读写算（教育教学研究），2014（38）.

·编辑 李建军