鼓式制动器热-应力-磨损耦合行为的研究*

张方宇，桂良进，范子杰

(清华大学，汽车安全与节能国家重点实验室,北京 100084)

2016075

鼓式制动器热-应力-磨损耦合行为的研究*

张方宇，桂良进，范子杰

(清华大学，汽车安全与节能国家重点实验室,北京 100084)

鼓式制动器在制动过程中，其温度场、应力场和磨损存在强烈的耦合现象。本文中首先将有限元技术和广义Archard磨损模型相结合，利用应力-磨损耦合分析方法，模拟了鼓式制动器的磨合过程；然后基于热-应力-磨损耦合算法模拟了制动器在单次制动过程中的热-应力-磨损耦合过程，展现了制动器的温度场、接触压力场和磨损的演变规律及其相互作用。最后，利用鼓式制动器台架试验对仿真结果进行验证，试验结果和仿真结果吻合良好。

鼓式制动器；温度；应力；磨损；有限元法

前言

鼓式制动器制动时存在复杂而强烈的热-应力-磨损耦合现象。摩擦片和制动鼓相互挤压产生接触压力和摩擦力。摩擦力做功生热，接触表层温度迅速升高至数百摄氏度。不均匀的热变形会改变摩擦片和制动鼓的接触压力场。另外，温度的升高还会改变摩擦片和制动鼓的硬度和界面摩擦因数，这也会改变接触压力和摩擦力的分布。反过来，摩擦力是生热的原因，其变化直接影响热传导过程。而上述过程中又伴随着磨损行为，反过来改变接触面形态，影响接触压力的分布。因此，制动过程伴随着温度场、应力场和磨损的相互耦合。

制动器热-应力-磨损耦合问题涉及复杂的几何结构和接触非线性，难以求得解析解。2000年以来，国内外许多学者利用有限元方法研究了制动器热-应力耦合作用过程[1-7]，然而研究对热边界条件做了许多简化，且完全忽略了磨损对温度场和位移场的影响。

20世纪末，磨损的有限元研究开始出现并流行。文献[8]中提出利用有限元方法求解滑动磨损问题，此后该方法越来越广泛地应用于模拟金属、陶瓷甚至聚合物的磨损现象。文献[9]中采用基于任意拉格朗日-欧拉(Arbitrary Lagrangian-Eulerian,ALE)技术的适应性磨损模型研究径向滑动轴承与转轴接触时的磨损过程，文中采用的ALE技术有效地打破了最大磨损小于表层单元高度的束缚。

目前，热-应力-磨损耦合问题的有限元研究尚处于起步阶段。文献[10]中提出了热弹性干磨损问题的有限元格式和迭代求解方案，然而该方法只适用于结构简单的平面问题，距离实际工程问题的应用仍有很大距离。文献[11]中研究了磨损对汽车制动器热弹性不稳定性的影响，但将连续体离散为孤立的线性二力杆单元，应力结果严重偏离实际情况。

本文中利用有限元技术研究了鼓式制动器热-应力-磨损耦合行为的瞬态特性。首先，利用应力-磨损耦合算法模拟了凸轮式鼓式制动器的磨合过程。然后，对鼓式制动器的三维模型展开瞬态制动和冷却分析。其中，制动分析考虑了热-应力-磨损的相互耦合作用，并且包含了材料热学参数的温度依赖性。最后，利用台架试验，对鼓式制动器的数值模拟结果进行验证，结果表明试验温度曲线与仿真结果吻合良好。

1 热-应力-磨损耦合的数学描述

1.1 热-应力耦合

根据制动器工作时的特点做以下假设：

(1)制动鼓、摩擦片和模型中的其它材料均满足各向同性和均匀性；

(2)模型所有变形均未进入塑性阶段，且没有阻尼，因此材料内部无热源；

(3)制动过程中，主要作用力为制动接触力和摩擦力，忽略惯性力的影响，因此力学分析采用准静态方式。

制动过程材料内部热传导满足方程：

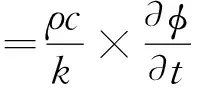
(1)

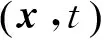
摩擦热流边界条件为

kφ·n=μpvr

(2)

式中:n为热流边界的单位法向量;μ为接触点的摩擦因数；p为接触压力；vr为相对滑动速率。

对流换热边界条件为

kφ

(3)

式中：ht为对流换热系数；φa为冷源温度。热传导方程的有限元格式[12]为

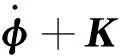
(4)

式中：Cφ为热容矩阵；Kφ为热传导矩阵；φ为节点温度向量；P为节点温度载荷向量，其中Pq为由摩擦生热引起的载荷向量，是接触压力p的函数，PH为由对流散热引起的载荷向量。

式(4)的增量格式为

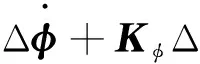
(5)

考虑热变形的静力分析有限元格式为

Kuu-KuφΔφ=fu

(6)

式中：Ku为节点位移对节点力的贡献矩阵;Kuφ为节点温升对节点力的贡献矩阵;u和fu分别为节点位移向量和节点力向量。

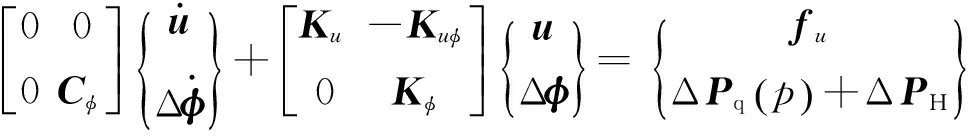
(7)

1.2 接触

物体A和B之间存在接触，接触面力满足动量平衡条件[13]：

tN≡tN，A(ΓC,t)=-tN，B(ΓC,t)≤0

(8)

式中:tN为面力的法向分量;ΓC为接触边界区域。

接触时相互不侵彻:

γN=vN，A-vN，B≤0

(9)

式中:γN为相互侵彻率;vN，A和vN，B分别为A和B接触点沿A物体表面外法向的速度分量。

另外，tN和γN存在如下归一化接触条件[13]:

tNγN=0

(10)

1.3 磨损

磨损的数值积分采用显式欧拉方法。广义Archard磨损模型的增量格式[14]为

Δh=κpΔs

(11)

式中：Δh为磨损厚度增量；κ为磨损系数；Δs为相对滑动位移增量。

假设制动鼓与摩擦片有限元网格的接触节点为i，积分步为j，则磨损增量为

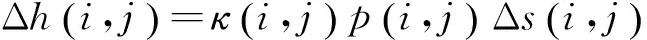
(12)

累积磨损量为

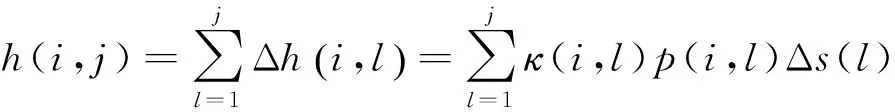
(13)

2 鼓式制动器磨合过程模拟

由于存在制造和安装误差，鼓式制动器初始使用时接触状况不佳。为了更加真实地模拟制动器在实际工作时热-应力-磨损耦合行为的特点，有必要对磨合过程进行模拟，以获得磨合后接触状况良好的有限元模型。

2.1 有限元模型

某重型载货车后桥鼓式制动器的有限元模型如图1所示。在ABAQUS中，制动鼓由2阶单元C3D20R模拟，摩擦片采用1阶单元C3D8R，制动蹄采用壳单元S4R，滚子利用解析刚体代替，凸轮轴采用2阶单元C3D20R。2阶单元可以更好地模拟复杂曲面，改善分析过程中的接触状况。

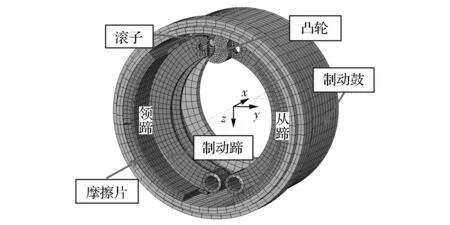
图1 磨合过程鼓式制动器有限元模型

制动鼓材料为HT250，制动蹄、滚子和凸轮均为钢材，摩擦片为复合材料，它们的参数分别见表1和表2。摩擦片的磨损系数κ=1.535×10-14Pa-1。

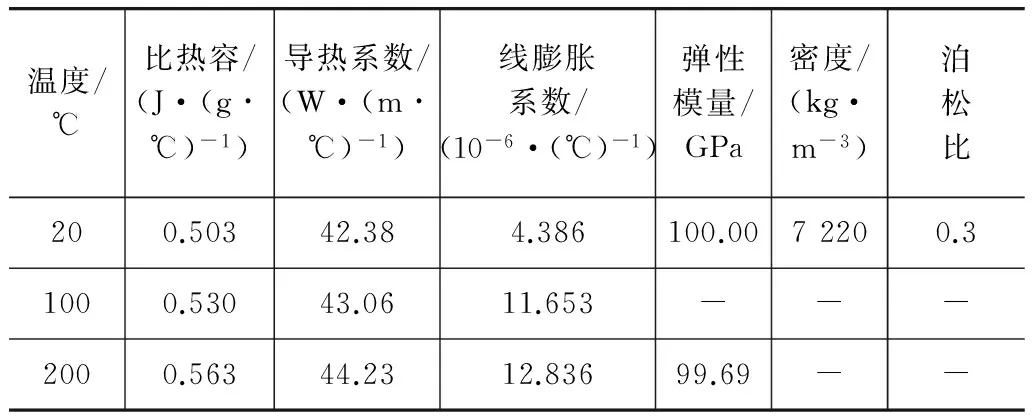
表1 制动鼓材料性能参数

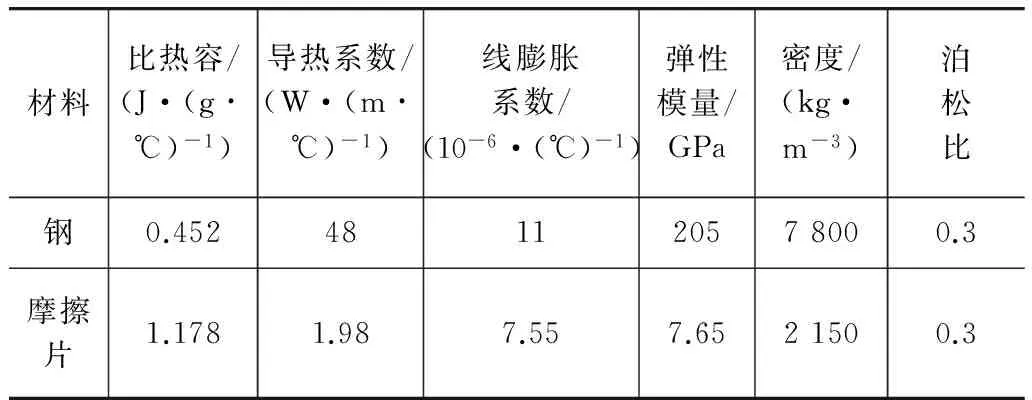
表2 钢和摩擦片的材料性能参数

磨合过程的边界条件如图2所示。仿真时，将制动鼓法兰部位的内柱面通过多点约束(MPC)耦合到旋转轴线的控制点上，如图2(a)所示。制动蹄下端与制动底板铰接，仿真时采用MPC将销孔内表面节点耦合到其轴线的控制点上，如图2(b)所示。制动蹄上端与滚子相连，因此也须将上端圆孔表面节点耦合到位于其轴线的控制点上。滚子为解析刚体，其主控点位于轴线上，滚子主控点与制动蹄上端控制点之间通过connector单元连接，如图2(c)所示。实际结构中，制动气室通过凸轮轴向凸轮传递转矩，在有限元模型中，将凸轮与轴连接的圆形区域通过Beam型MPC耦合到位于凸轮轴轴线的主控点上，如图2(d)所示。

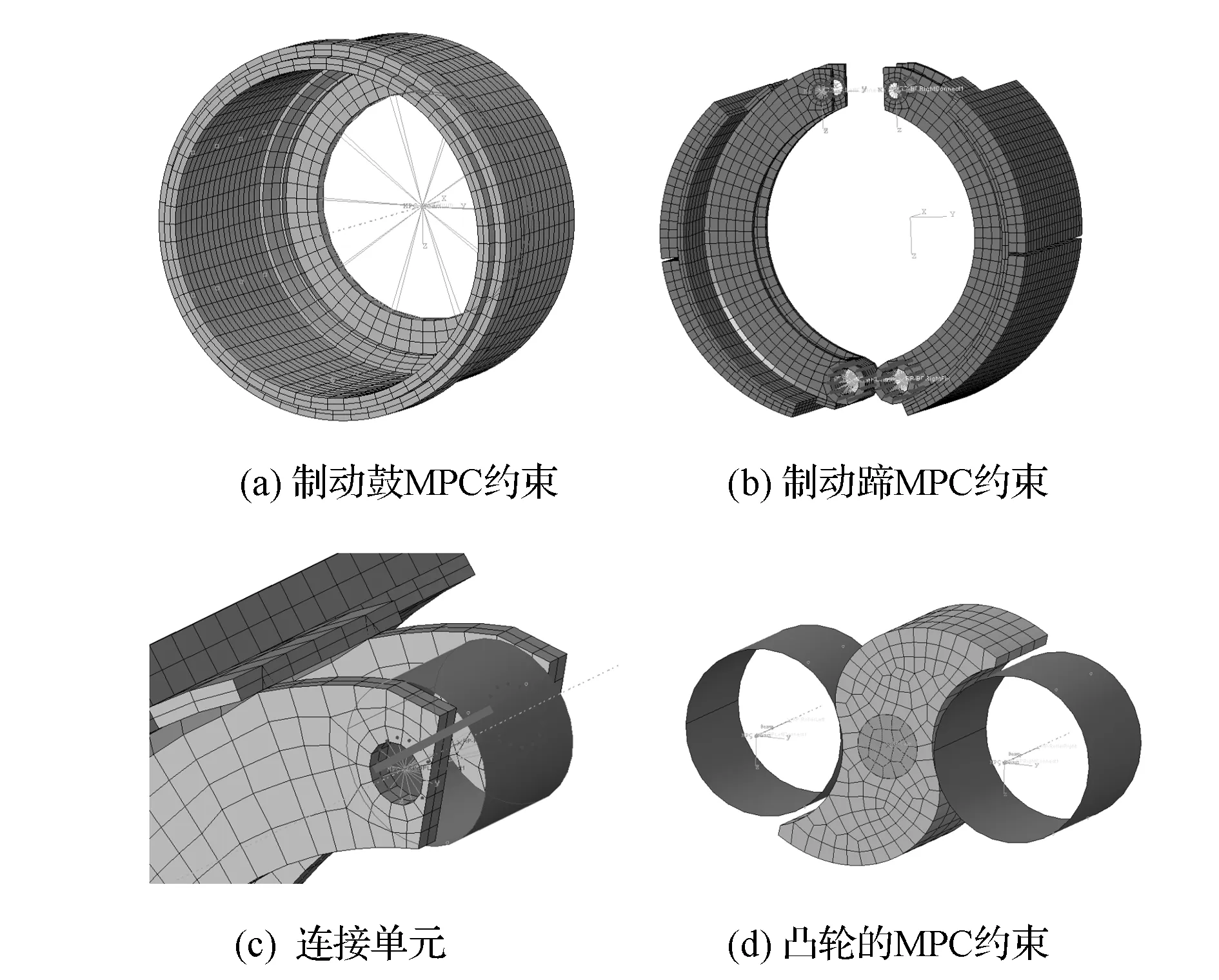
图2 磨合过程的边界条件

制动鼓与摩擦片之间设置接触，制动鼓内表面为主面，摩擦片外表面为从面，接触算法为罚函数法，摩擦因数为0.35。摩擦片与制动蹄之间设置Tie约束。凸轮与滚子之间设置无摩擦接触，滚子为主面，凸轮为从面，接触算法为罚函数法。

2.2 求解方法

磨合过程不考虑温度场，采用应力-磨损耦合分析方法模拟。忽略惯性力效应，属于准静态过程，在应力分析的相邻增量步之间利用UMESHMOTION子程序计算磨损量和磨损方向，再应用ALE技术更新有限元网格，实现磨损的仿真，即在一个增量步中先更新应力再更新磨损量。

首先预加位移载荷，使各接触对的接触计算收敛。然后取消位移载荷，对凸轮添加转矩。最后令制动鼓控制点以ω=26.455rad/s恒速旋转，开始磨合仿真。仿真过程中忽略制动鼓的磨损，将摩擦片材料设置为ALE作用域，摩擦片的表面节点通过UMESHMOTION子程序计算磨损。为了加快仿真速度，可将摩擦片磨损速率适当加倍。

2.3 仿真结果与分析

摩擦片接触压力的演变如图3所示。图3(a)为初始时刻的压力分布，图3(b)为磨合完成时刻的接触压力分布。由图可见，摩擦片绝大部分区域已经进入接触。

图3 磨合过程接触压力分布图

初始时刻，接触压力分布非常不均匀，最大值达6.73MPa。领蹄由于增势作用，接触压力大于从蹄。另外，初始时刻无论是领蹄还是从蹄，最大接触压力出现在摩擦片上下两端。

磨合开始后，接触压力大的区域磨损快，因此随着磨损的进行，接触压力大的区域接触状况得到改善，接触压力小的区域接触压力逐渐增加，而未接触的区域逐渐进入接触。到磨合结束时，最大接触压力降到1.45MPa，接触压力的分布更加均匀。磨合结束时，领蹄完全进入接触，从蹄绝大部分区域进入接触。

在磨合过程中，接触压力沿着制动鼓轴向分布也存在着一定特点。图3中，领蹄的左侧是制动鼓法兰方向，右侧是制动鼓开口方向，而从蹄的朝向正好相反。磨合结束时，无论领蹄还是从蹄，摩擦片靠近制动鼓法兰的部位接触压力大于靠近制动鼓开口的部位。制动鼓法兰一侧受到螺栓约束，刚度比较大，而开口一侧刚度较小，因此出现了上述现象。

3 鼓式制动器单次制动过程模拟

3.1 有限元模型

磨合过程完成后，摩擦片与制动鼓之间接触良好，接近正常使用情况。单次制动仿真考虑温度场的影响，分为2个步骤:(1)制动载荷步，时间长度2.58s，制动鼓从26.5rad/s匀减速到0;(2)冷却载荷步，时间长度为60s，制动鼓转速维持在2.1rad/s。

由于仿真涉及温度场，而摩擦片导热性差，温度梯度大，因此加密摩擦片厚度方向的网格数量为4层。摩擦片采用热-应力耦合分析的1阶单元C3D8RT。为避免温度场数值产生振荡，制动鼓也采用1阶单元C3D8RT。

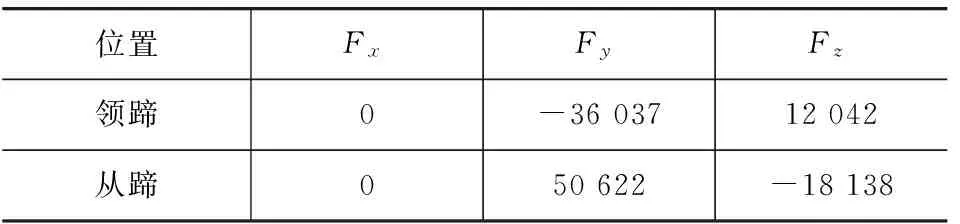
表3 单次制动凸轮对制动蹄载荷 N

制动鼓与摩擦片之间接触传热热流密度为

(14)

式中：q为热流密度；hc为接触传热系数；φr和φl分别为制动鼓和摩擦片的温度。

当制动鼓与摩擦片之间处于接触状态时，设置接触传热系数为较大值，保证接触点温度相同。在制动过程中，当制动鼓与摩擦片处于未接触状态时，其最大间隙只有10-4m量级，假定制动鼓和摩擦片之间的间隙主要由磨屑填充。忽略磨屑的吸热，则接触传热系数可近似为

hc=λl/dgap

(15)

式中：λl为摩擦片的导热系数；dgap为接触间隙。

制动鼓在转动过程中与周围环境存在对流换热，对流换热系数[15]为

(16)

式中：hR为制动鼓外表面与环境之间的对流换热系数；λa为空气的导热系数；D为制动鼓外径；Re为以制动鼓外径为特征长度的雷诺数。

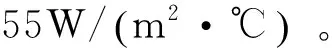
3.2 求解方法

采用热-应力-磨损完全耦合方法求解，其流程如图4所示。

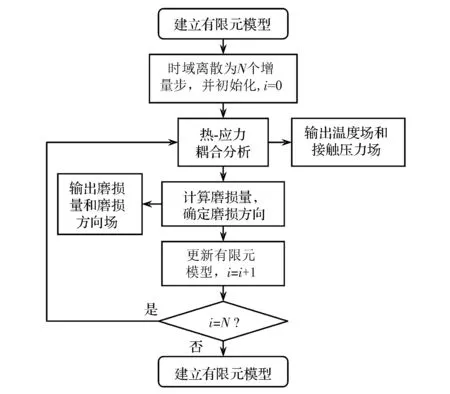
图4 完全耦合分析方法流程图

制动鼓的磨损量远小于摩擦片，因此仿真中只考虑摩擦片的磨损。制动载荷步设置ALE作用域为整体摩擦片材料，通过UMESHMOTION子程序计算摩擦片表面节点的磨损。

3.3 仿真结果与分析

制动过程中接触压力的分布如图5所示。领蹄由于增势作用整个摩擦片进入接触，且接触压力分布相对均匀，而从蹄中间部位未进入接触，上端接触力较大。另外，领蹄左侧和从蹄右侧均靠近制动鼓的法兰端，因此接触压力相比另一端大。

图5 单次制动接触压力分布图

制动结束时摩擦片的磨损量如图6所示。一次制动过程中，摩擦片表面各点滑移距离几乎相等，因此磨损量的分布和接触压力的分布形式非常相似。单次制动磨损量非常小，最大值为0.72m。

图6 单次制动摩擦片磨损量

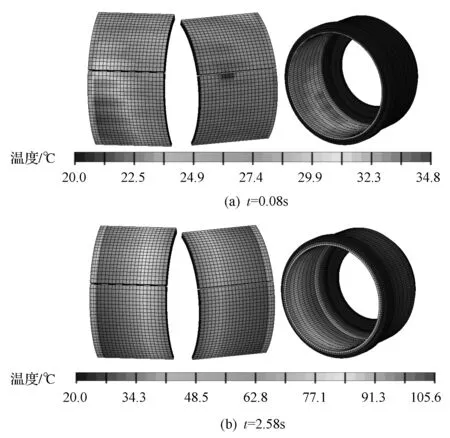
图7 制动载荷步温度场的演变图

制动过程中制动鼓和摩擦片的温度变化如图7所示，从左到右依次为领蹄、从蹄和制动鼓。由图可见，t=0.08s时，摩擦片和制动鼓的温升不大，但分布不均匀。摩擦热流功率与接触压力成正比，因此，领蹄摩擦片温升高于从蹄摩擦片。另外，摩擦片靠近制动鼓法兰一侧接触压力大于另一侧，其温升也比较高。制动鼓在旋转过程中受热逐渐均匀，呈现近似轴对称的温度分布。摩擦片与制动鼓之间导热良好，因而摩擦片的温度也趋于轴对称分布。当t=2.58s时，制动结束，最高温度达到105.6oC，制动鼓内表面和摩擦片外表面温度相差不大。

冷却过程中，制动鼓和摩擦片的温度分布如图8所示，从左到右依次为领蹄、从蹄和制动鼓。

图8 冷却载荷步温度场的演变图

冷却过程开始前，制动鼓与摩擦片处于接触状况，因此制动鼓与摩擦片表面温度几乎相同(见图7)。当制动鼓与摩擦片不再接触而冷却开始后，两者相对的表面开始出现温度差别(见图8)。冷却初始阶段，热量迅速从制动鼓内表面向外表面传递，而摩擦片材料的导热性较差，温度下降缓慢。因而t=10s时，制动鼓内表面温度低于摩擦片外表面温度。随着热传导过程的进行，制动鼓内外表面温差减小，温度变化逐渐缓慢，而摩擦片由于导热而持续降低。因此当t=60s时，制动鼓内表面温度高于摩擦片外表面温度。另外，冷却过程中，制动鼓温度仍然保持近似轴对称分布。而摩擦片由于本身结构及其与空气之间的对流边界均为非轴对称，温度分布并不保持近似轴对称分布。

4 单次制动仿真结果的试验验证

鼓式制动器台架试验在陕西汉德车桥有限公司的实验中心完成，图9为试验台架。鼓式制动器的主要零部件包括制动鼓、制动蹄和凸轮轴，如图10所示。

图9 鼓式制动器试验台架

图10 鼓式制动器主要零部件

图11 从蹄测温点位置

制动器完成磨合后，开始单次制动试验，制动参数与数值模拟相同。制动过程中温度变化由热电偶监测，从蹄测温点分别位于蹄片上端、中部和下端，如图11所示，领蹄摩擦片布置了两个热电偶，分别位于上端和中间。

图12 单次制动摩擦片测温点温度变化曲线

单次制动的试验与仿真结果的温度变化曲线对比如图12所示。图中，1#表示领蹄，2#表示从蹄，U,M和D分别表示上端、中部和下端。其中，0-2.58s为制动过程，这段时间内制动鼓动能迅速转化为摩擦热量被制动鼓和摩擦片吸收，2.58-60s为冷却过程。在0-10s内，摩擦片吸收的热量逐渐传递到测温点处，这段时间内温度很快上升到峰值温度。随后，热量逐渐向制动蹄方向传导，测温点处的温度逐渐下降，表现出冷却的趋势。仿真曲线与试验曲线吻合良好，最大温度差别为2℃左右。

5 结论

本文中基于有限元分析开发了鼓式制动器热-应力-磨损耦合算法，对鼓式制动器的磨合与单次制动过程进行了数值模拟，对比了磨损对温度和接触压力分布的影响。其中，磨合过程采用应力-磨损耦合仿真算法，结果展现了接触压力的演变过程。单次制动过程采用热-应力-磨损完全耦合仿真算法，结果揭示了单次制动过程中温度场、接触压力和磨损的演变特点及相互作用。最后，进行了鼓式制动器的制动台架试验，试验测得的温度变化曲线与数值仿真结果吻合良好。

研究结果表明：(1)磨合过程中，领蹄接触压力大于从蹄，领从蹄两端接触压力大于中间区域，摩擦片靠近制动鼓法兰端接触压力大于开口端，接触压力的分布随着磨合过程逐渐趋于均匀；(2)制动鼓温度场近似轴对称分布，摩擦片靠近制动鼓法兰端温度高于开口端。

[1] 吕振华,亓昌.蹄-鼓式制动器热弹性耦合有限元分析[J].机械强度,2003,25(4):401-407.

[2] 范久臣.汽车鼓式制动器多物理场仿真研究及数字化分析平台[D].长春:吉林大学,2009.

[3] 余为高.通风盘式制动器热—机耦合仿真分析及寿命预测[D].广州:华南理工大学,2010.

[4] 陈友飞.盘式制动器热与热力耦合分析模型建立与仿真计算研究[D].北京:清华大学,2011.

[5] 张建辉.鼓式制动器热弹性耦合非线性有限元分析[D].武汉:武汉科技大学,2012.

[6]HECKMANNA.ABrakeModelwithThermoelasticDiscfortheAnalysisofVehicleJudderVibrations[J].VehicleSystemDynamics,2006,44:360-367.

[7]BELHOCINEA,BOUCHETARAM.TransientAnalysisofThermoelasticContactProblemofDiskBrakes[J].FrontiersofMechanicalEngineering,2013,8(2):150-159.

[8]PODRAP,ANDERSSONS.SimulatingSlidingWearwithFiniteElementMethod[J].TribologyInternational,1999,32(2):71-81.

[9]REZAEIA,VANPAEPEGEMW,DEBAETSP,etal.AdaptiveFiniteElementSimulationofWearEvolutioninRadialSlidingBearings[J].Wear,2012,296:660-671.

[10]IREMANP,KLARBRINGA,STRÖMBERGN.FiniteElementAlgorithmsforThermoelasticWearProblems[J].EuropeanJournalofMechanics-A/Solids,2002,21(3):423-440.

[11]OSTERMEYERGP,GRAFM.InfluenceofWearonThermoelasticInstabilitiesinAutomotiveBrakes[J].Wear,2013,308(1):113-120.

[12] 王勖成. 有限单元法[M]. 北京: 清华大学出版社,2003.

[13]BELYTSCHKOT,LIUWK,MORANB. 连续体和结构的非线性有限元 [M].庄茁，译.北京: 清华大学出版社,2002:495-528.

[14]SODERBERGA,ANDERSSONS.SimulationofWearandContactPressureDistributionatthePad-to-RotorInterfaceinaDiscBrakeUsingGeneralPurposeFiniteElementAnalysisSoftware[J].Wear,2009,267(12):2243-2251.

[15]DAYAJ,NEWCOMBTP.DissipationofFrictionalEnergyfromtheInterfaceofanAnnularDiscBrake[J].ProceedingsoftheInstitutionofMechanicalEngineers,PartD:TransportEngineering,1984,198(11):201-209.

A Study on the Heat-Stress-Wear Coupling Behavior of Drum Brake

Zhang Fangyu, Gui Liangjin & Fan Zijie

TsinghuaUniversity,StateKeyLaboratoryofAutomotiveSafetyandEnergy,Beijing100084

The strong coupling effects between temperature field, stress field and wear of drum brake in braking process are studied in this paper. Firstly, by combining finite element technique and generalized Archard wear model, with stress-wear coupling analysis method adopted, the running-in process of drum brake is simulated. Then, based on coupled heat-stress-wear algorithm, a single braking process is simulated to show the evolution rules of and the interaction between these three fields. Finally, a bench test is conducted for verification, with a result well agreeing with the simulated one.

drum brake; temperature; stress; wear; FEM

*国家自然科学基金(51175280，51475255)资助。

原稿收到日期为2014年11月19日，修改稿收到日期为2015年2月9日。