机载波谱仪海浪谱反演方法及其验证

李秀仲, 何宜军, 孟俊敏, 张振华

(1. 南京信息工程大学, 江苏 南京 210044; 2. 国家海洋局第一海洋研究所, 山东 青岛 266061; 3. 北京遥测技术研究所, 北京 100076)

机载波谱仪海浪谱反演方法及其验证

李秀仲1, 何宜军1, 孟俊敏2, 张振华3

(1. 南京信息工程大学, 江苏 南京 210044; 2. 国家海洋局第一海洋研究所, 山东 青岛 266061; 3. 北京遥测技术研究所, 北京 100076)

为了验证波谱仪反演二维海浪谱的功能, 根据海浪波谱仪的信号形成机制, 总结了机载波谱仪反演海浪的流程。利用机载波谱仪回波数据, 通过自相关和互相关两种功率谱估计方法, 反演了二维海浪谱。最后通过与浮标测量的二维海浪谱进行对比, 验证了该机载波谱仪探测二维海浪谱的有效性。结果表明, 无论采用自相关函数还是互相关函数进行功率谱估计, 得到的主波波长和有效波高与实际二维海浪谱基本一致。互相关函数法得到的交叉谱能去除180°模糊现象, 其在计算有效波高时相对于自相关函数会稍微偏小。在计算斜率方差时可以采用5°~12°入射角范围的后向散射系数进行公式拟合, 因此定标与否并不影响最后的二维海浪谱结果, 未来星载波谱仪只有靠多波束联合才能实现。

波谱仪; 功率谱估计; 二维海浪谱; 180°模糊

海况信息的获取有着重要的业务化需求(如海洋气象预报、导航、近海和沿海活动等)和科研需求(海浪动力分析、大气和海洋边界层的相互作用、区域和整体的海洋和大气系统耦合, 电磁信号与海面相互作用等)。过去几十年, 虽然海浪预报已经进步很大[1], 但是在高海况条件、极值事件(如台风、风暴潮等)方面还有很大的改进余地; 在提供准确参数预报方面不仅可以预报有效波高, 还可以改进峰值波长和波向预报。目前应用的海浪数值模式在预测二维海浪谱方面面临很大缺点[1], 比如海浪激发源和耗散项的参数化以及采用的初始场存在误差较大等。此外, 由于数值模型离散化的限制, 在海浪能量的方向分布上, 开阔海域时会产生较大误差, 这样就会导致波浪在靠近海岸时的演化结果中产生更大的预报误差。

目前唯一星载测量海浪的雷达系统是合成孔径雷达(Synthetic Aperture Radar, SAR)。自从Seasat卫星上搭载了SAR后[2], SAR就一直比较昂贵并且在测量海浪方向谱时并不简单易用。为了去除SAR这种限制, 人们发展了其它类型雷达: Walsh等[3]1985开发了Ka波段的海面等值线雷达(surface contour radar, SCR), Jackson等[4-5]1985年开发了Ku波段雷达海浪波谱仪(Radar Ocean Wave Spectrometer, ROWS), Hauser等[6]1992年开发了C波段雷达测波仪(Radar pour l’Etude du Spectre des Surfaces par AnalyseCirculaire, RESSAC), Hauser等[7]2003年开发了C波段极化雷达观测系统(Système de Télédétection pour l’Observation par Radar de la Mer, STORM), 以及Plant等[8]2005年开发了X波段相干真实孔径雷达(coherent real aperture radar, CORAR)。这些机载测量雷达比方向浮标提供了更多的海浪方向性信息[9]。

中法海洋卫星(China–France Oceanography Satellite, CFOSAT)是一个由中国和法国空间机构正在准备的新卫星。它是为了同步海浪谱和海面风场观测而设计的。该卫星上将搭载一个Ku波段的散射计测量风速, Ku波段的波谱仪(Surface Waves Investigation and Monitoring, SWIM)来测量海面浪场。CFOSAT是一个极轨卫星, 飞行高度为520 km。SWIM雷达能向海面发射6个不同入射角的波束: 0°、2°、4°、6°、8°和10°, 每个波束天线孔径都是2°,天线旋转速度是5.6 rad/min。SWIM能提供如下的地球物理参数: 0°~10°入射角的标准化后向散射系数(normalized radar cross-section, NRCS); 星下点的有效波高和风速; 6°、8°、10°波束能提供海浪方向谱。

在CFOSAT的准备阶段, 北京遥测技术研究所开发了机载波谱仪, 并在山东半岛以南的黄海区域进行了校飞试验, 以检验SWIM测量海浪方向谱的能力。本文针对机载波谱仪70圈的回波数据, 通过总结国内外反演算法, 反演了二维海浪方向谱, 并与浮标实测的二维海浪谱对比, 检验了波谱仪测量海浪二维谱的有效性, 为星载波谱仪的反演算法的开发奠定了基础。

图1 处理的波谱仪校飞试验数据所在轨迹Fig. 1 Tracks of the processed data obtained using an airborne sea-wave spectrometer

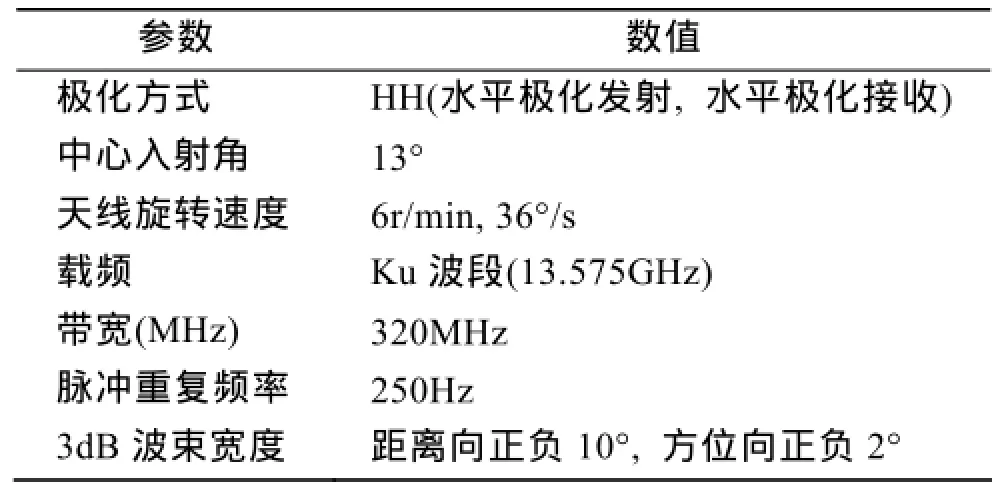
表1 机载波谱仪主要参数Tab. 1 Main parameters of the airborne sea-wave spectrometer

1 机载波谱仪校飞介绍

机载波谱仪的校飞试验位置选在黄海北部, 图1中三角形和六角形分别为2014年6月12日10: 21和2014年6月21日11: 07浮标所在位置(分别是122.84°E、36.62°N和122.61°E、36.62°N), 浮标每半小时给出一个海浪谱结果。校飞时无风速计实测风速, 但根据浮标所测海浪波高较小可知, 两个架次的风速在2~5 m/s变化。三角形附近的粗曲线为飞机2014年6月12日11: 6: 20~11: 11: 20共301 s的飞行轨迹, 也是本文处理的30圈回波数据的轨迹, 始末位置相差15.62 km, 起始位置与浮标相差7.17 km;细直线为飞机2014年6月21日10: 48: 58~10: 55: 37共400 s的飞行轨迹, 是本文处理的40圈的回波数据轨迹, 始末位置相差28.54 km, 与六角形所代表的浮标最近距离约为11.58 km。

对于机载波谱仪, 由于飞行高度不可能达到卫星的高度, 因此采用一个大波束, 以增加足印面积。该机载波谱仪的主要参数在表1中给出。

图2显示了此次机载波谱仪校飞的几何示意图,根据3 dB波束宽度, 每个脉冲在海面上形成的等天线增益值线可以简化成一个椭圆形状。根据倾斜调制的原理, 雷达接收图中椭圆内圆环里的海面反射能量, 当波浪局地倾斜导致的海面法线对着雷达时海面回波强, 反之当波浪局地倾斜导致的海面法线偏离雷达时, 雷达接收的回波弱。因此雷达信号变化的幅值与海浪局地倾角有关。根据Jackson等[4-5]、Hauser等[10], 海面斜率与后向散射系数的关系为:

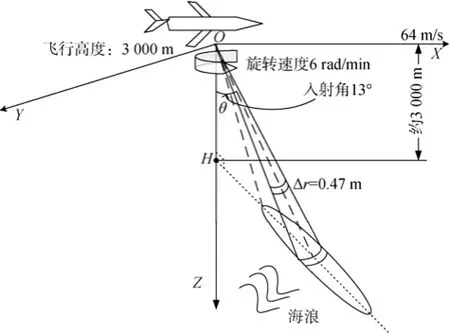
图2 机载波谱仪观测几何Fig. 2 Geometry of observation of the airborne sea-wave spectrometer

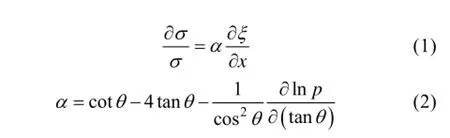
式中, p为海面斜率概率密度函数, a为定标参数,x为波面高度, q为入射角。因此获取海面斜率的雷达调制信号, 求取调制信号功率谱, 可得某一方向的海浪斜率谱通过雷达天线360°水平面旋转, 即可得到二维方向谱, 即公式(3)中的

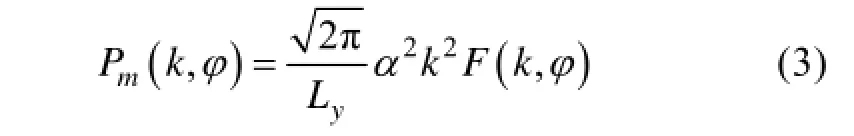
式中，Ly为波束方位向3 dB宽度,为调制谱, k为波数, j为方位角。

图3模拟了机载波谱仪校飞1 min形成的足迹。波谱仪在海面形成的足迹与以下几个参数有关: 飞机飞行高度、飞机飞行速度、天线旋转速度以及脉冲重复频率。为了显示清晰, 该图只显示了5 Hz的脉冲重复频率结果, 飞行高度为3 000 m、飞机飞行速度为60 m/s、天线转速是6 rad/min。考虑到准镜面散射理论适用范围以及其水平分辨率因素, 图中展示了入射角5°~12°时的波束足印, 水平径向距离为375 m, 短半轴长则为214 m。

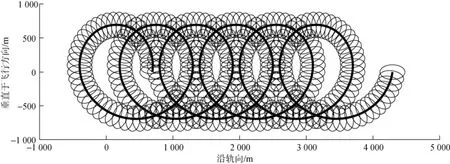
图3 机载波谱仪探测足迹Fig. 3 Footprint detected by the sea-wave spectrometer

2 机载海浪谱反演方法

本文根据波谱仪的工作原理, 在国内外波谱仪研究基础上, 采用以下流程进行了二维海浪谱的反演。

图4中, 回波数据是雷达接收的不同时刻电磁波能量, 天线增益是由实验室实测后的二维天线增益经过飞机姿态角校正后得到的增益[11], r代表斜距, m( r)是沿斜距的调制信号, 由本文公式(4)中的组成, x是水平距离,是沿水平方向的调制信号。此处海浪斜率谱为由调制谱根据公式(3)转换得到斜率谱为标准化过程,j为方位角。

2.1 计算0σ

波谱仪获取回波能量之后, 为了获取海浪的无量纲的标准化后向散射系数0s, 采用雷达方程为

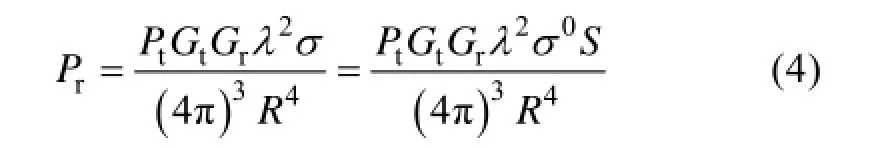
式中,rP和tP是接收和发射的能量, R是斜距,tG和rG是天线发射和接收的增益, l是单位为米的载频电磁波长。雷达接收的截面(Radar Cross-Section, RCS)s用公式(5)表达

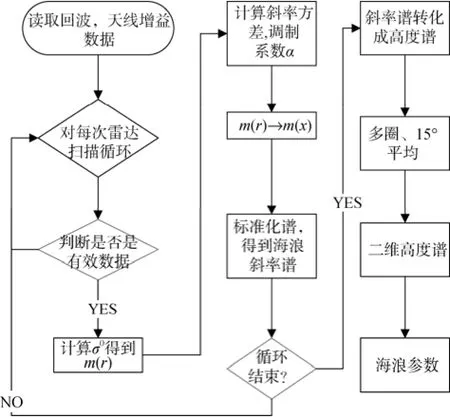
图4 机载波谱仪海浪谱反演方法Fig. 4 Retrieving method of sea-wave spectrum using an airborne spectrometer

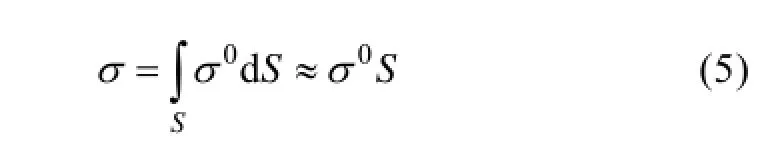
S是电磁波波束照射的面积, 这个面积能够用一个矩形的宽度dx和长度dy来表示, 并且是方位向的波束宽度, 所以。将此公式代入公式(4), 并令可得到公式(6)

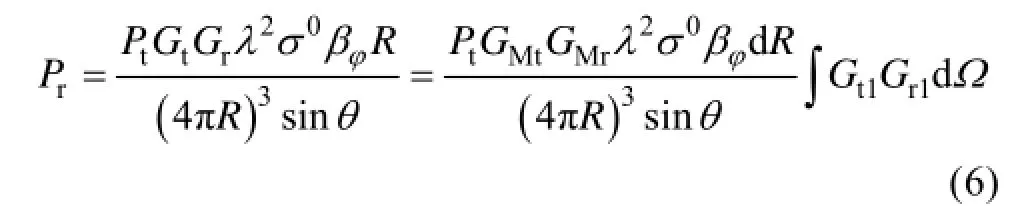
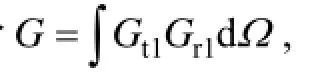
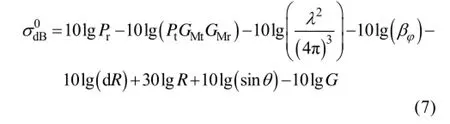
2.2 计算斜率方差和调制系数

基于小入射角下NRCS, 有一个简便的方法能用来计算斜率方差(mean square slope, MSS)。Barrick[12]和Valenzuela[13]导出了有限粗糙面的电磁散射公式, 总结出小入射角范围是0°~15°时准镜面散射是海面散射的主要部分。准镜面散射公式是此处天底点的菲尼尔反射系数,是二维海面斜率概率密度分布函数, zx表示距离向海面斜率, zy表示方位向海面斜率。正比于满足条件的微小面元的数量, 所以也可以写成。如果是高斯分布, 那么等式(8)变成

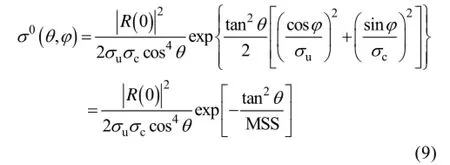
此处us和cs分别是海面斜率在逆风向和侧风向的标准偏差。MSS是方位角j处的斜率方差。如果海面斜率概率分布函数(Probability Density Function, PDF)是高斯的, 那么我们可以得到[14-15]

所以, 当0s通过式(7)获取后, 利用方位角j处的回波对上式拟合, 可以获取MSS。此处选择5°入射角作为拟合上限是考虑了地面分辨率随着入射角减小而变差这个因素。Freilich等[16]假设入射角0°~18°时降雨雷达散射能量在海面风速0~20 m/s范围内主要是由准镜面散射机制产生的, 其中较大入射角时布拉格散射机制变得相对重要了。此处选择12°入射角作为上限并假设此时准镜面散射占主要部分是合适的。需要注意的是, 我们获取的是系数的负倒数, 所以0s是否进行了定标并没有关系。

根据海面斜率分布近似高斯函数形式的结论,则通过公式(2)调制系数计算公式变为

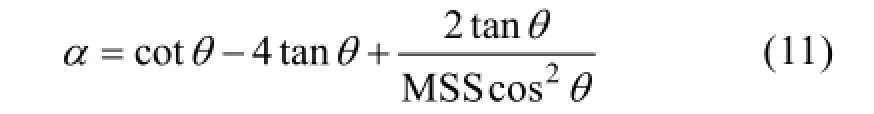
由于海浪谱是由信号调制谱得来的, 因此计算海浪谱之前, 需要通过调制信号计算调制谱。采用两种方法估计调制谱, 第一种是自相关函数功率谱估计方法

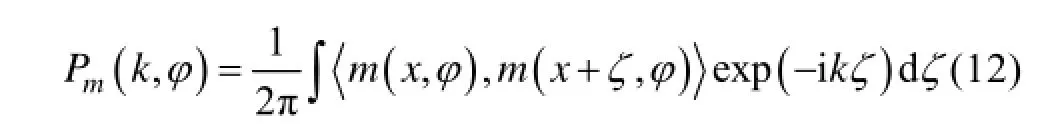
该方法是采用同一信号进行自相关得到的功率谱, 在进行谱估计之前, 需要对调制信号进行加窗处理, 以消除由于信号截断造成的频谱泄露问题。第二种是交叉谱估计方法

j¢为同圈内与j有一定时间间隔的方位角, 交叉谱计算时, 主要针对相邻的两个回波, 以达到去除噪声的目的。

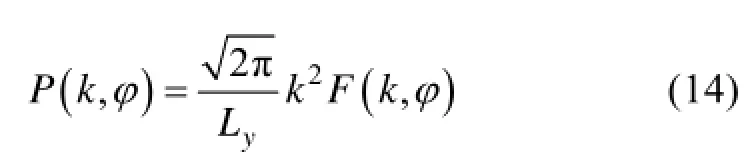
这两种方法求取的海浪谱都存在180°模糊的问题, 本文借鉴SAR消除180°模糊的方法[17], 根据公式(13)中求取的互相关函数, 则观测到的海浪传播的径向轨道速度为

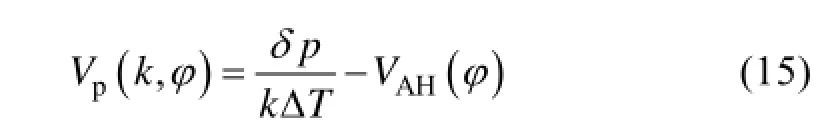
2.4 海浪参数的确定

有效波高(significant wave height, SWH)HSW代表了海浪能量的大小, 其计算公式为

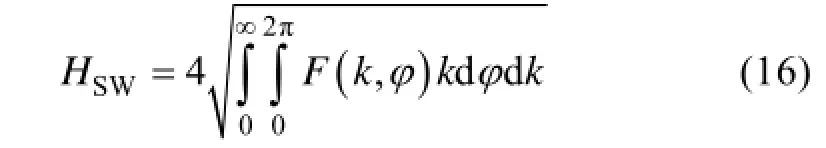
主波波数kp为F(k,j)最大值所对应的波数, 主波波长则为主波波向为方向谱取最大值处对应的方向j。在求取浮标所测海浪谱主波波长和主波波向时, 对于浮标提供的频率谱, 需要转换成波数谱。根据

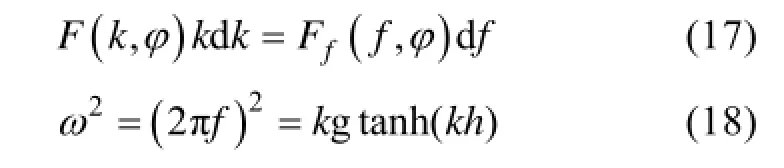
w是角频率, f为波浪频率, h和g分别为水深和重力加速度, 水深h在30 m左右, 根据上式可以得到每个频率对应的波数。

3 二维海浪谱及其参数的验证

浮标测量的二维海浪谱如图5、图6所示, 其中HSW分别为0.47, 0.6 m, 主波波长是83, 39 m, 波浪传播方向是南偏东20°, 12°, 若正北为0°, 逆时针为正, 则浪向为200°, 192°。

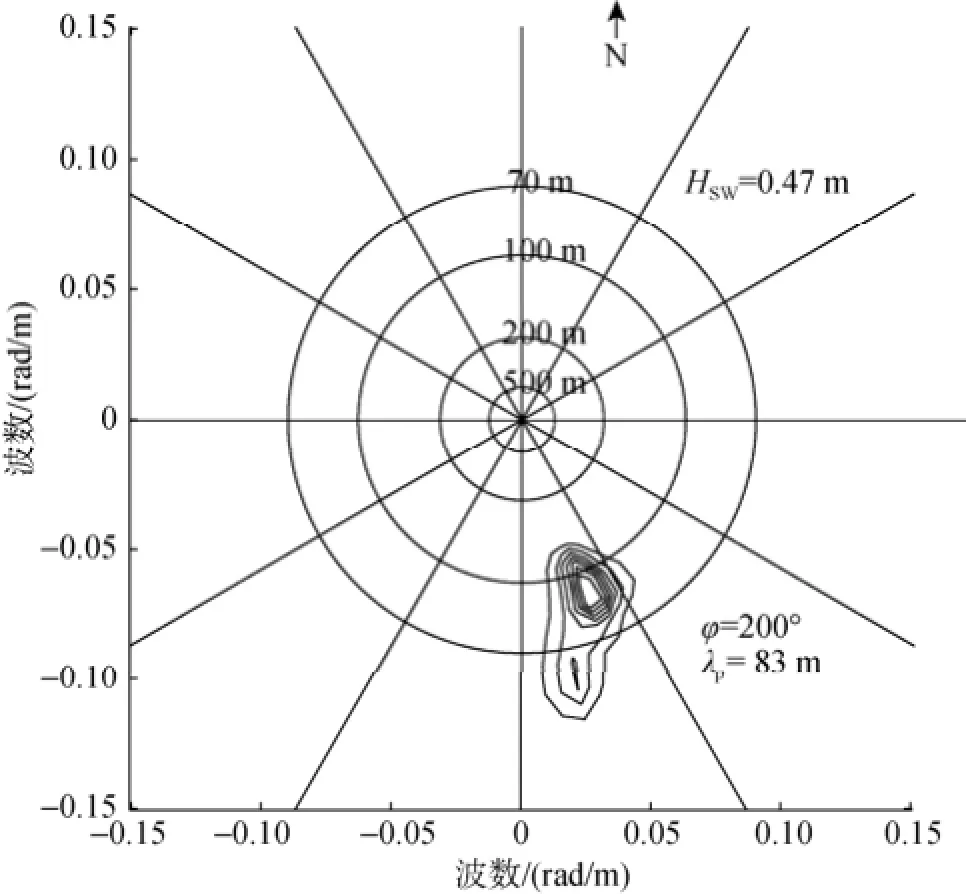
图5 2014年6月12日10: 21波浪骑士所测二维海浪谱Fig. 5 Two-dimensional spectrum detected from a sea wave rider at 10: 21 on June 12, 2014

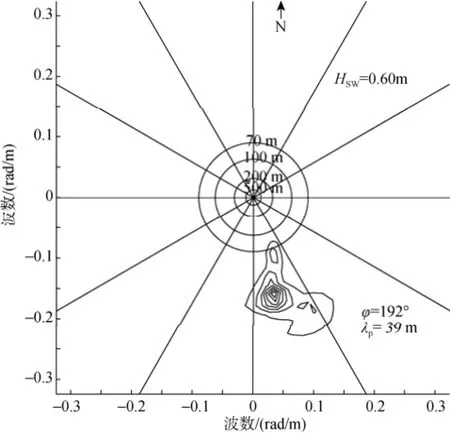
图6 2014年6月21日11: 07波浪骑士所测二维海浪谱Fig. 6 Two-dimensional spectrum detected from a sea wave rider at 11: 07 on June 21, 2014

由于本次校飞时海况较低, 因此海浪信息并不够规则, 此处将这两块数据所得结果各自进行了平均。利用前面两种功率谱计算方法得到两种海浪谱反演结果如下图, 对于第一块数据, 自相关函数方法得到的结果显示, 主波波长93 m, 波浪传播方向为30°, 与浮标结果相反, 有效波高为0.46 m。而交叉谱方法得到的这3个参数分别为93 m、210°、0.41 m, 海浪传播方向基本与浮标所测结果一致。

第2块数据中, 自相关函数方法得到的主波波长、波浪传播方向、有效波高分别为128 m, 270°和 0.57 m, 交叉谱方法得到的这3个参数分别为37 m、170°、0.55 m。很显然, 该结果中自相关函数法由于噪声的影响无法测得正确的结果。

图7 2014年6月12日自相关函数法所得海浪谱Fig. 7 Sea-wave spectrum obtained from the auto-correlation method on June 12, 2014

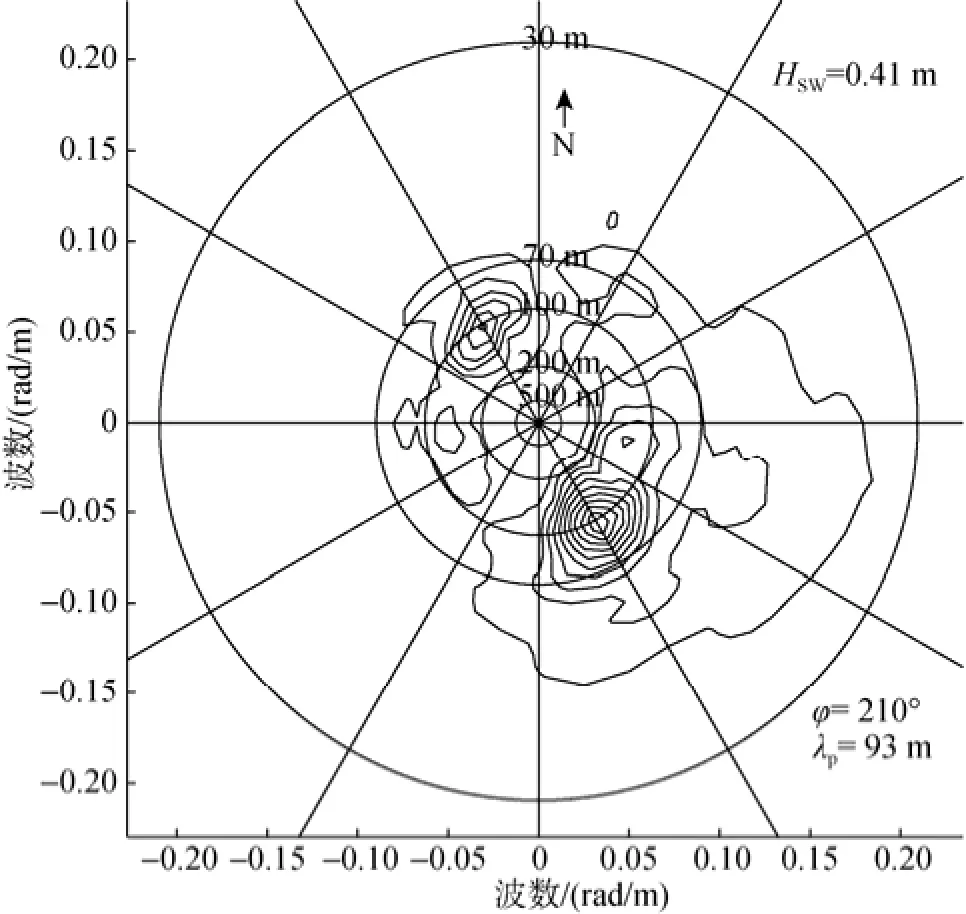
图8 2014年6月12日互相关函数法所得海浪谱Fig. 8 Sea-wave spectrum obtained from the cross-correlation method on June 12, 2014

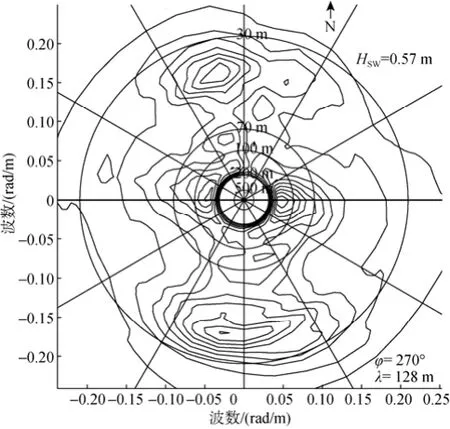
图9 2014年6月21日自相关函数法所得海浪谱Fig. 9 Sea-wave spectrum obtained from the auto-correlation method on June 21, 2014

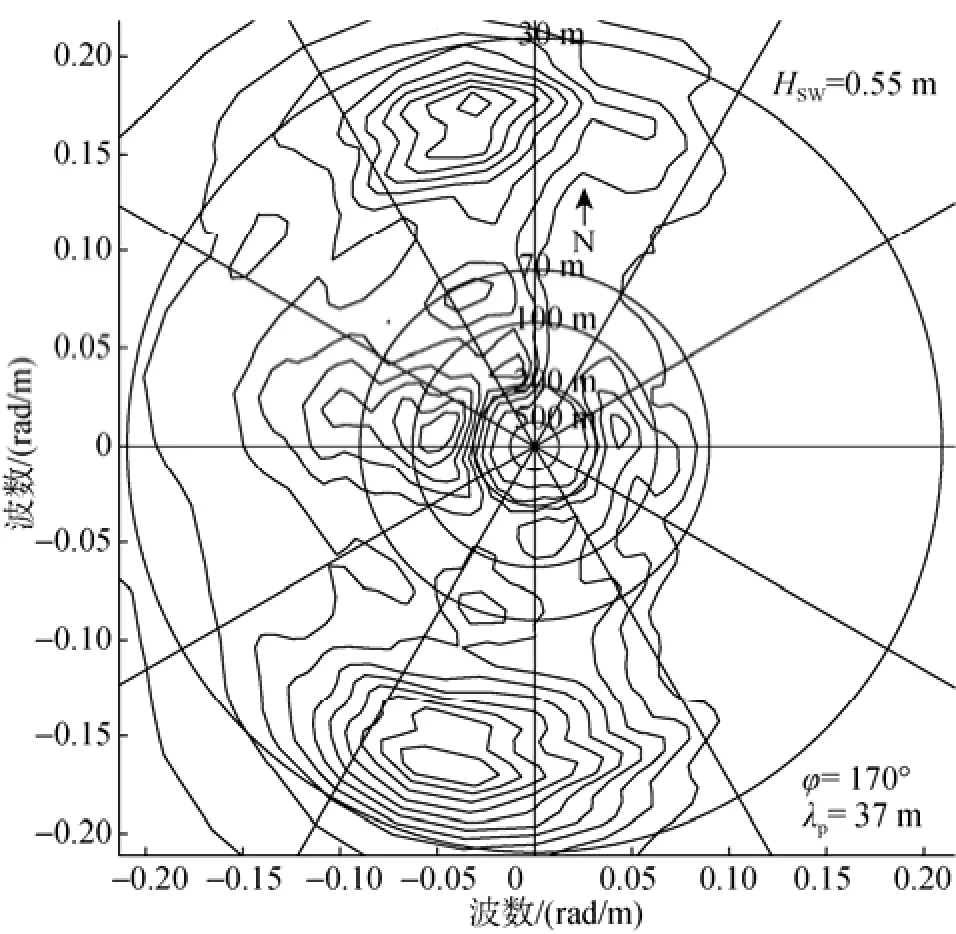
图10 2014年6月21日互相关函数法所得海浪谱Fig. 10 Sea-wave spectrum obtained from the cross-correlation method on June 21, 2014

这两种功率谱估计方法所测主波波长和有效波高与浮标一致性都较好, 误差在可接受范围之内。根据交叉谱方法中相位差的方法, 基本可以去除180°模糊。图7显示方位向30°时能量大于210°, 这应该是由于在210°方位向时异常回波较多, 因此会有较多的回波被删除掉, 导致结果显示波浪传播在30°方位向。图8中显示有几圈180°模糊并没有去除掉, 因此会在30°方位向时产生一个较小的峰值。交叉谱方法得到的有效波高较小, 这应该与互相关函数功率谱估计的过程中用到了相邻两束回波进行互相关,相关性强度必定会比自相关函数减弱, 但这样做的优点是可以去除两束回波中不相关的信息, 对去噪有一定帮助。

若都采用互相关函数法, 6月12日结果得到的海浪传播方向10°的误差比21日22°的误差小, 但主波波长10 m的误差大于21日2 m的误差。12日和21日校飞时海面有效波高分别是0.47 m和0.6 m, 所以海况均很小, 若单独处理出某几圈的结果, 误差会较大, 因此本文两块数据分别进行了30圈数据的平均和40圈数据的平均。通过本次结果处理可知, 交叉谱方法得到的海浪谱在去除180°模糊方面有较大优势, 并且在去噪方面有一定优势, 因此交叉谱比自相关函数谱更有优势。由于此次校飞试验所在的海况环境较低, 对于更高海况和更大的飞行高度尚没有试验, 以及风浪和涌浪混合时海浪反演的准确性无法得到验证。

4 结论

本文分析了二维海浪谱的近实时探测在业务化和科研方面的需求, 介绍了未来中法星星载波谱仪探测海浪谱的几何特性, 根据机载波谱仪校飞试验和机载波谱仪的信号形成机制, 总结了波谱仪反演海浪的流程, 并利用该流程处理了机载校飞的回波数据, 通过自相关函数和互相关函数两种功率谱估计方法, 反演了二维海浪谱。最后根据浮标得到的二维海浪谱对机载波谱仪探测二维海浪谱的有效性进行了验证, 并对比了两种海浪谱计算方法。主要结论如下:

1) 工作在Ku 波段的机载海洋波谱仪是一种真实孔径雷达系统, 波谱仪波束基于长波对海面微尺度波的倾斜调制, 通过方位向360°扫描测量海浪谱,通过本文的验证, 这种方法探测二维海浪谱以及波向、波长和有效波高是有效的。

2) 根据波谱仪信号形成机制, 采用互相关函数进行功率谱估计在获取主波波长、波向和有效波高时, 能与浮标所测结果较为一致且精度较高。交叉谱方法相对于自相关函数方法能去除海浪传播的180°模糊, 因此交叉谱方法更有优势。

3) 互相关函数法得到的交叉谱, 在计算有效波高时会偏小, 这与互相关函数功率谱估计的方法有关。由于互相关法进行时, 两个回波信号必须有差别,因此相关强度会变弱, 导致结果总能量偏小。海浪信息越规则, 这两种方法结论就会越一致。

4) 在计算斜率方差时采用了5°~12°入射角范围进行公式拟合, 根据本文结论可知, 低海况时定标与否对最后反演的二维海浪谱结果不会产生决定性影响, 但该方法对于更高海况适用性尚未可知。未来星载波谱仪只有靠多波束联合才能实现。

致谢: 非常感谢北京遥测技术研究所提供的机载波谱仪数据和国家海洋局第一海洋研究所提供的浮标数据。

[1] Cavaleri L. Wave modeling: Where to go in the future[J]. Bulletin of the American Meteorological Society, 2006, 87(2): 207-214.

[2] Gonzalez F I, Beal R C, Brown W E, et al. Seasat synthetic aperture radar: Ocean wave detection capabilities[J]. Science, 1979, 204(4400): 1418-1421.

[3] Walsh E J, Hancock III D W, Hines D E, et al. Directional wave spectra measured with the surface contour radar[J]. Journal of Physical Oceanography, 1985, 15(5): 566-592.

[4] Jackson F C, Walton W T, Peng C Y. A comparison of in situ and airborne radar observations of ocean wave directionality[J]. Journal of Geophysical Research: Oceans (1978–2012), 1985, 90(C1): 1005-1018.

[5] Jackson F C, Walton W T, Baker P L. Aircraft and satellite measurement of ocean wave directional spectra using scanning-beam microwave radars[J]. Journal of Geophysical Research: Oceans, 1985, 90(C1): 987-1004.

[6] Hauser D, Caudal G C, Rijckenberg G J, et al. RESSAC: A new airborne FM/CW radar ocean wave spectrometer[J]. Geoscience and Remote Sensing, 1992, 30(5): 981-995.

[7] Danièle H, Podvin T, Dechambre M, et al. Polarimetric measurements over the sea-surface with the airborne STORM radar in the context of the geophysical validation of the ENVISAT ASAR[J/OL]. [2015-09-17]. http: //earth.esa.int/workshops/polinsar2003/participants/ hauser5/POLINSAR-VALPARESO.pdf, 2003.

[8] Plant W J, Keller W C, Hayes K. Simultaneous measurement of ocean winds and waves with an airborne coherent real aperture radar[J]. Journal of Atmospheric and Oceanic Technology, 2005, 22(7): 832-846.

[9] Pettersson H, Graber H C, Hauser D, et al. Directional wave measurements from three wave sensors during the FETCH experiment[J]. Journal of Geophysical Research:Oceans (1978–2012), 2003, 108(C3): 209.

[10] Hauser D, Soussi E, Thouvenot E, et al. SWIMSAT: A real-aperture radar to measure directional spectra of ocean waves from space-main characteristics and performance simulation[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18(3): 421-437.

[11] Li Xiuzhong, He Yijun, Zhang Biao, et al. The construction of a three-dimensional antenna gain matrix and its impact on retrieving sea surface mean square slope based on aircraft wave spectrometer data[J]. Journal of Atmospheric and Oceanic Technology, 2016, 33(4): 847-856.

[12] Barrick D E. Rough surface scattering based on the specular point theory[J]. Antennas and Propagation, 1968, 16(4): 449-454.

[13] Valenzuela G R. Theories for the interaction of electromagnetic and oceanic waves-A review[J]. Boundary-Layer Meteorology, 1978, 13(1-4): 61-85.

[14] Jackson F C, Walton W T, Hines D E, et al. Sea surface mean square slope from Ku-band backscatter data[J]. Journal of Geophysical Research: Oceans (1978–2012), 1992, 97(C7): 11411-11427.

[15] Hesany V, Plant W J, Keller W C. The normalized radar cross section of the sea at 10 incidence[J]. Geoscience and Remote Sensing, 2000, 38(1): 64-72.

[16] Freilich M H, Vanhoff B A. The relationship between winds, surface roughness, radar backscatter at low incidence angles from TRMM Precipitation Radar measurements[J]. J Atmos Ocean Technol, 2003, 20(4): 549-562.

[17] Engen G, Johnsen H. SAR-ocean wave inversion using image cross spectra[J]. Geoscience and Remote Sensing, 1995, 33(4): 1047-1056.

Received:Dec. 24, 2015

Retrieval method of an ocean wave spectrum using an airborne spectrometer and performing the validation

LI Xiu-zhong1, HE Yi-jun1, MENG Jun-min2, ZHANG Zhen-hua3
(1. Nanjing University of Science Information and Technology, Nanjing 210044, China; 2. First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China; 3. Beijing Research Institute of Telemetry, Beijing 100076, China)

spectrometer; power spectrum estimation; two-dimensional ocean wave spectra; 180° ambiguity

The ocean wave retrieval method is designed on the basis of the signal formation principle of an ocean wave spectrometer. By using the spectra estimation methods via the auto-correlation and cross-correlation functions, the two-dimensional ocean wave spectrum is obtained. Finally, after comparing the spectrum received from the buoy and that retrieved from the spectrometer, the effectiveness of detecting a two-dimensional spectrum from an airborne spectrometer is evaluated. We observe that in the environment of flight, the results of the methods using the auto-correlation and cross-correlation functions for retrieving ocean wave spectrum are consistent with that obtained from the buoy. From the cross spectrum, the ambiguity of 180° is excluded, although the significant wave height is smaller than that from auto-correlation method. When the sea-slope variance is calculated, the radar backscattering coefficients of the incidence angles at 5°–12° are fitted. Therefore, calibration of the radar backscattering coefficients is not required. Moreover, the future spaceborne spectrometer will be able to attain calibration of the radar backscattering coefficients using multibeam joints.

P731.22; TP732.1

A

1000-3096(2016)12-0123-08

10.11759/hykx20151224004

(本文编辑: 李晓燕)

2015-12-24;

2016-03-19

国家重点研发计划子课题(2016YFC1401005); 江苏省自然科学基金项目(BK2011008); 国家自然科学基金(41476158); 江苏省高等教育优势学科项目

[Foundation: Research and Development of the National Key Program Corpus, No.2016YFC1401005; Natural Science Foundation of Jiangsu Province, No.BK2011008; National Science Foundation of China, No.41476158; The Preponderant Discipline Project of High Education in Jiangsu Province]

李秀仲(1985-), 山东济宁人, 博士研究生, 主要从事海洋微波遥感研究, E-mail: qdlixiuzhong@163.com; 何宜军, 通信作者,教授, 博士生导师, E-mail: yjhe@nuist.edu.cn